Конденсатор в цепи постоянного и переменного тока
Конденсатор в цепи постоянного тока
Итак, берем блок питания постоянного напряжения и выставляем на его крокодилах напряжение в 12 Вольт. Лампочку тоже берем на 12 Вольт. Теперь между одним щупом блока питания и лампочки вставляем конденсатор:

Не-а, не горит.
А вот если напрямую сделать, то горит:

Отсюда напрашивается вывод: постоянный ток через конденсатор не течет!
Если честно, то в самый начальный момент подачи напряжения ток все-таки течет на доли секунды. Все зависит от емкости конденсатора.
Конденсатор в цепи переменного тока
Итак, чтобы узнать, течет ли переменный ток через конденсатор, нам нужен генератор переменного тока. Думаю, этот генератор част оты вполне сойдет:

Так как китайский генератор у меня очень слабенький, то мы вместо нагрузки-лампочки будем использовать простой резистор на 100 Ом. Также возьмем и конденсатор емкостью в 1 микрофарад:

Спаиваем как-то вот так и подаем сигнал с генератора частоты:

Далее за дело берется Цифровой осциллограф OWON SDS 6062. Что такое осциллограф и с чем его едят, читаем зде сь. Будем использовать сразу два канала. На одном экране будут высвечиваться сразу два сигнала. Здесь на экранчике уже видны наводки от сети 220 Вольт. Не обращайте внимание.
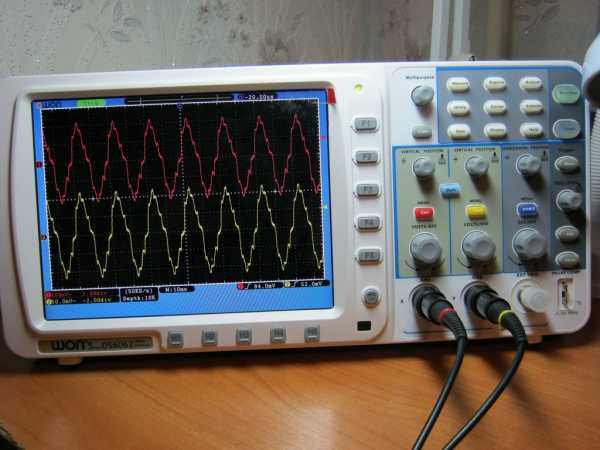
Будем подавать переменное напряжение и смотреть сигналы, как говорят профессиональные электронщики, на входе и на выходе. Одновременно.
Все это будет выглядеть примерно вот так:

Итак, если у нас частота нулевая, то это значит постоянный ток. Постоянный ток, как мы уже видели, конденсатор не пропускает. С этим вроде бы разобрались. Но что будет, если подать синусоиду с частотой в 100 Герц?
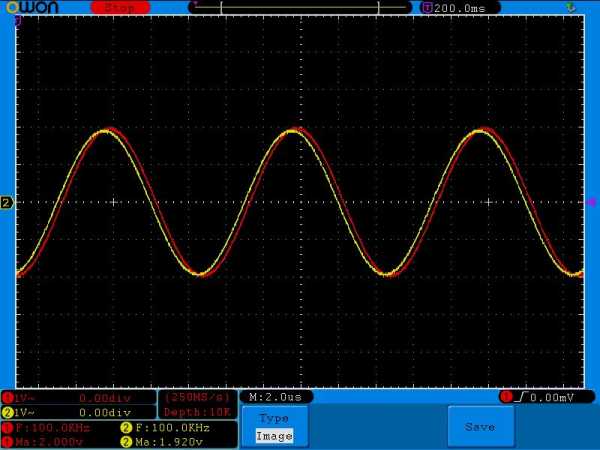
На дисплее осциллографа я вывел такие параметры, как частота сигнала и его амплитуда: F – это частота, Ma – амплитуда (эти параметры пометил белой стрелочкой). Первый канал помечен красным цветом, а второй канал – желтым, для удобства восприятия.
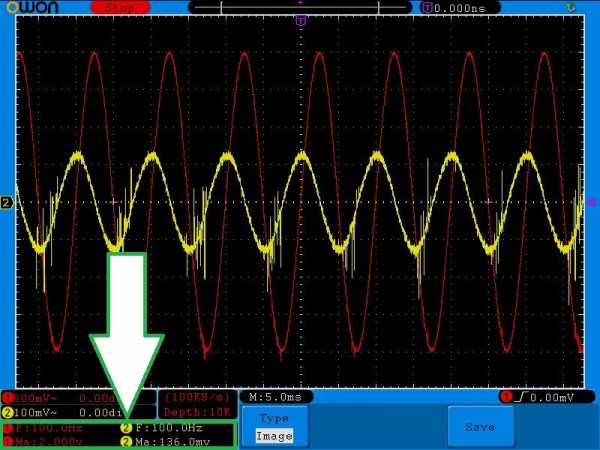
Красная синусоида показывает сигнал, который выдает нам китайский генератор частоты. Желтая синусоида – это то, что мы уже получаем на нагрузке. В нашем случае нагрузкой является резистор. Ну вот, собственно, и все.
Как вы видите на осциллограмме выше, с генератора я подаю синусоидальный сигнал с частотой в 100 Герц и амплитудой в 2 Вольта. На резисторе мы уже видим сигнал с такой же частотой (желтый сигнал), но его амплитуда составляет каких-то 136 милливольт. Да еще и сигнал получился какой-то “лохматый”. Это связано с так называемыми “шумами“. Шум – это сигнал с маленькой амплитудой и беспорядочным изменением напряжения. Он может быть вызван самими радиоэлементами, а также это могут быть помехи, которые ловятся из окружающего пространства. Например очень хорошо “шумит” резистор. Значит “лохматость” сигнала – это сумма синусоиды и шума.
Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается влево, то есть опережает красный сигнал, или научным языком, появляется сдвиг фаз. Опережает именно фаза, а не сам сигнал. Если бы опережал сам сигнал, то у нас бы тогда получилось, что сигнал на резисторе появлялся бы по времени раньше, чем сигнал, поданный на него через конденсатор. Получилось бы какое-те перемещение во времени :-), что конечно же, невозможно.
Сдвиг фаз – это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:
Давайте увеличим частоту на генераторе до 500 Герц
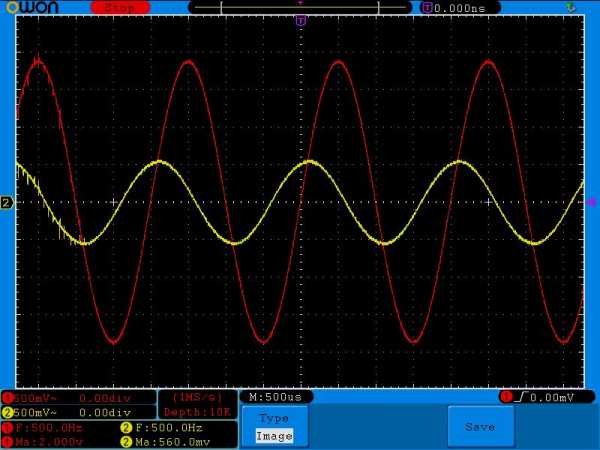
На резисторе уже получили 560 милливольта. Сдвиг фаз уменьшается.
Увеличиваем частоту до 1 КилоГерца
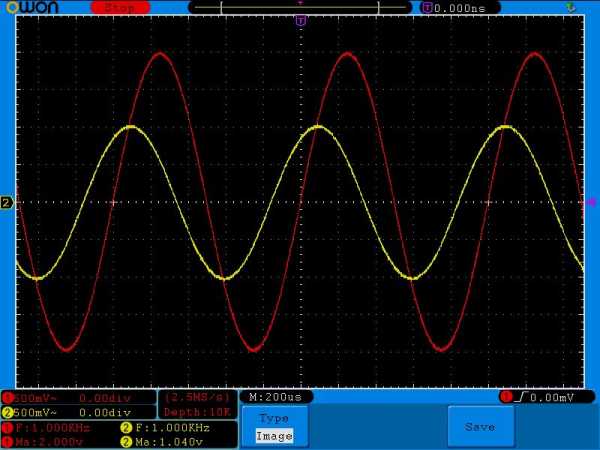
На выходе у нас уже 1 Вольт.
Ставим частоту 5 Килогерц
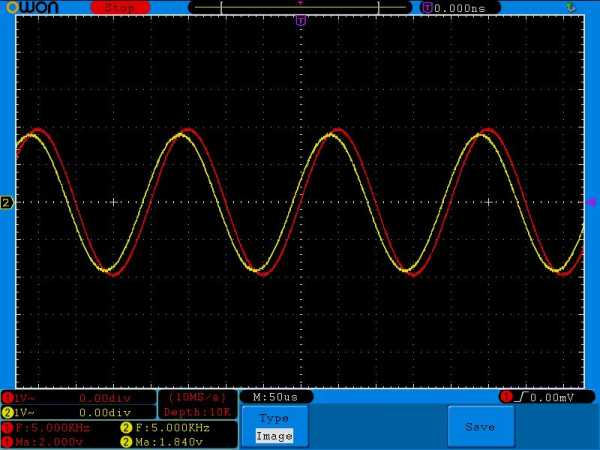
Амплитуда 1,84 Вольта и сдвиг фаз явно стает меньше
Увеличиваем до 10 Килогерц
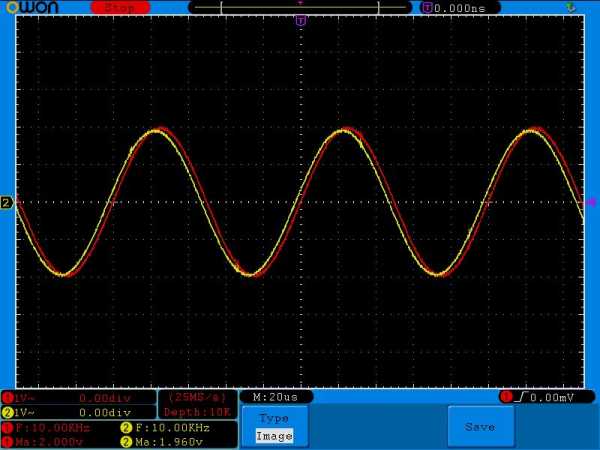
Амплитуда уже почти такая же как и на входе. Сдвиг фаз менее заметен.
Ставим 100 Килогерц:
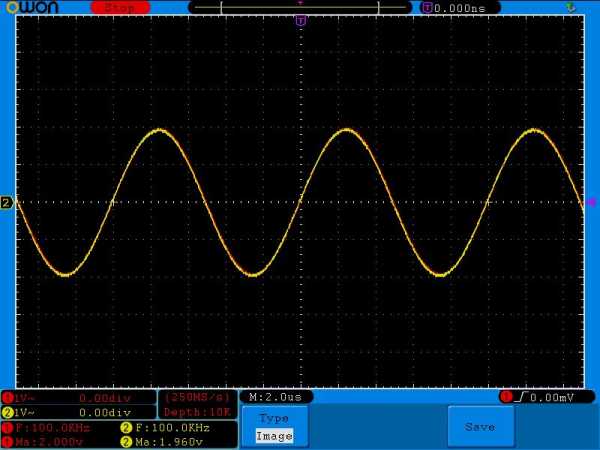
Сдвига фаз почти нет. Амплитуда почти такая же, как и на входе, то есть 2 Вольта.
Отсюда делаем глубокомысленные выводы:
Чем больше частота, тем меньшее сопротивление конденсатор оказывает переменному току. Сдвиг фаз убывает с увеличением частоты почти до нуля. На бесконечно низких частотах его величина составляет 90 градусов или π/2.
Если построить обрезок графика, то получится типа что-то этого:
По вертикали я отложил напряжение, по горизонтали – частоту.
Итак, мы с вами узнали, что сопротивление конденсатора зависит от частоты. Но только ли от частоты? Давайте возьмем конденсатор емкостью в 0,1 микрофарад, то есть номиналом в 10 раз меньше, чем предыдущий и снова прогоним по этим же частотам.
Смотрим и анализируем значения:
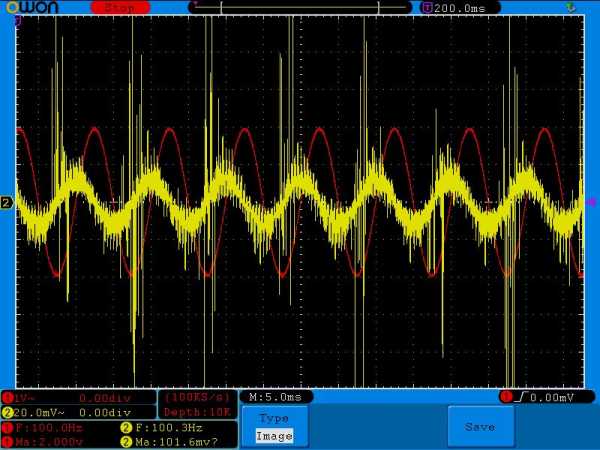
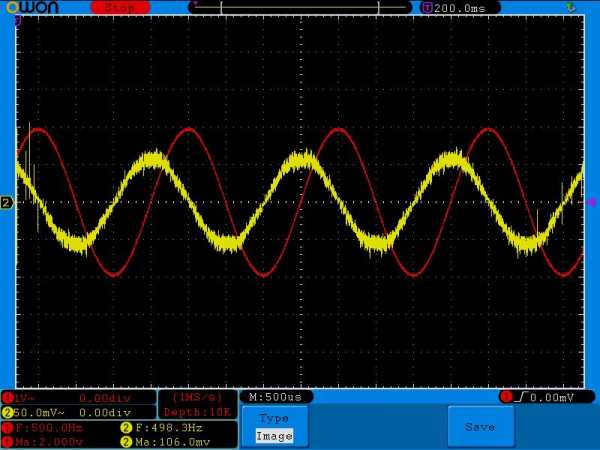
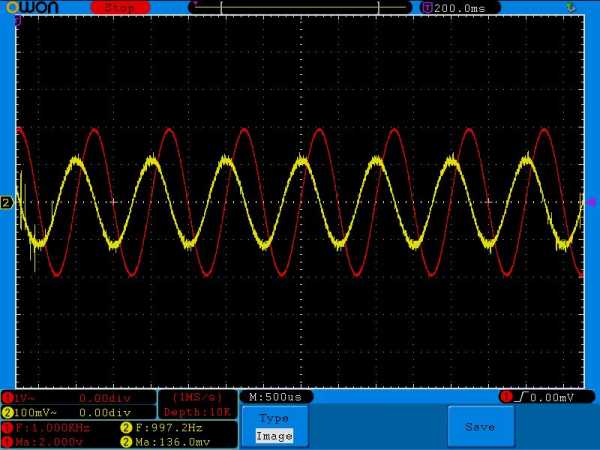
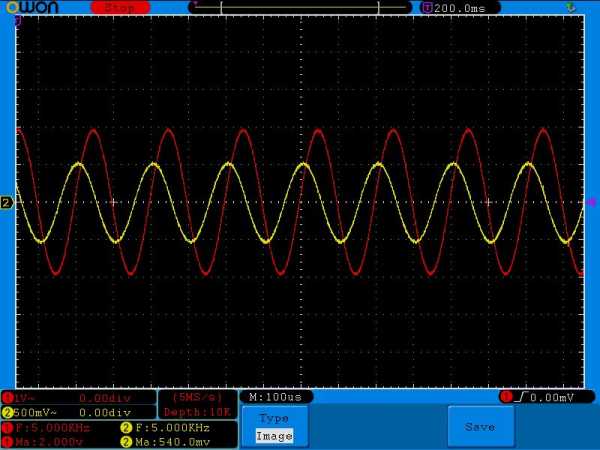
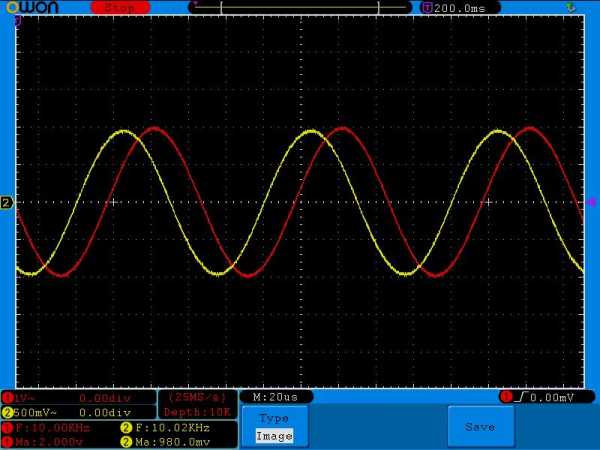
Внимательно сравните амплитудные значения желтого сигнала на одной и той же частоте, но с разными номиналами конденсатора. Например, на частоте в 100 Герц и номиналом конденсатора в 1 мкФ амплитуда желтого сигнала равнялась 136 милливольт, а на этой же самой частоте амплитуда желтого сигнала, но с конденсатором в 0,1 мкФ уже была 101 милливольт( в реальности еще меньше из за помех). На частоте 500 Герц – 560 милливольт и 106 милливольт соответственно, на частоте в 1 Килогерц – 1 Вольт и 136 милливольт и так далее.
Отсюда вывод напрашивается сам собой: при уменьшении номинала конденсатора его сопротивление стает больше.
С помощью физико-математических преобразований физики и математики вывели формулу для расчета сопротивления конденсатора. Прошу любить и жаловать:
где, ХС – это сопротивление конденсатора, Ом
П – постоянная и равняется приблизительно 3,14
F – частота, измеряется в Герцах
С – емкость, измеряется в Фарадах
Так вот, поставьте в эту формулу частоту в ноль Герц. Частота в ноль Герц – это и есть постоянный ток. Что получится? 1/0=бесконечность или очень большое сопротивление. Короче говоря, обрыв цепи.
Заключение
Забегая вперед, могу сказать, что в данном опыте мы получили Фильтр Высокой Частоты (ФВЧ). С помощью простого конденсатора и резистора, применив где-нибудь в звуковой аппаратуре такой фильтр на динамик, в динамике мы будет слышать только писклявые высокие тона. А вот частоту баса как раз и заглушит такой фильтр. Зависимость сопротивления конденсатора от частоты очень широко используется в радиоэлектронике, особенно в различных фильтрах, где надо погасить одну частоту и пропустить другую.
www.ruselectronic.com
Конденсатор в цепи постоянного тока
Заряд конденсатора через резисторПри подключении конденсатора к источнику постоянного тока под действием электрического поля на нижнюю обкладку движутся электроны. В следствии, явления электростатической индукции с верхней обкладки конденсатора заряды уходят к положительному выводу источника питания в цепи возникает ток – ток заряда по мере накопления зарядов в конденсаторе, растёт напряжение , а ток заряда уменьшается, и так, – конденсатор подключённый к источнику тока, заряжается до Uист.
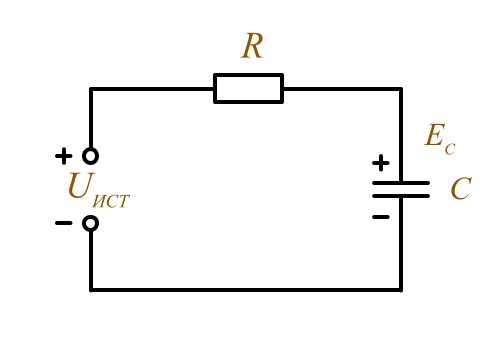
Конденсатор в цепи постоянного тока
Кратковременный ток в цепи называется ток заряда, а так как он существует короткое время, то говорят, конденсатор
Считается что конденсатор заряжается если напряжение на нём составляет 0,63 от Uист и это происходит за время
равное Τ
Ес – ЭДС ёмкости
Τ заряда – постоянная времени заряда конденсатора в секундах
Одна секунда – 1с = 103мс = 106мкс =1012нс
Rзар – сопротивление в Омах
С – ёмкость в Фарадах
Τ = Rзар × С
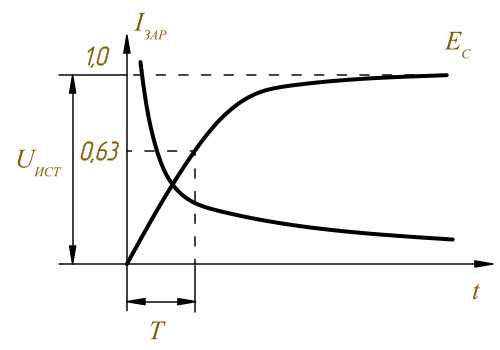
График заряда конденсатора
Разряд конденсатора через резистор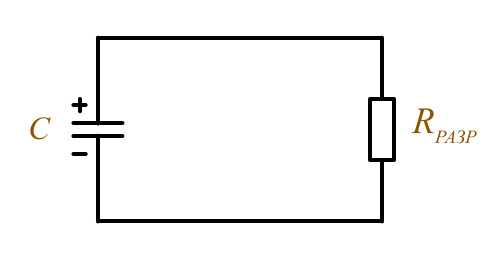
Работа конденсатора в цепи постоянного тока
Считается, что конденсатор разрядится если напряжение на нём составляет 0,37 от напряжения источника и это происходит за время Τ разряда.
Τразр = Rразр × С
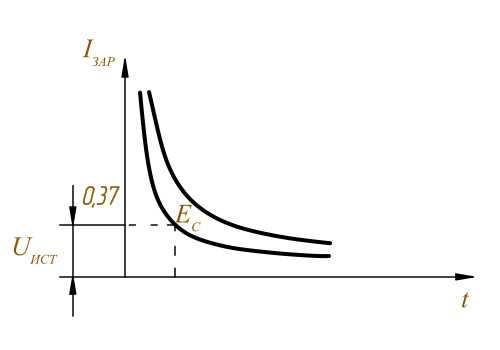
График разряда конденсатора
Конденсатор в цепи переменного и постоянного тока: что это такое, виды
Элементная база для конструирования электронных устройств усложняется. Приборы объединяются в интегральные схемы с заданным функционалом и программным управлением. Но в основе разработок – базовые приборы: конденсаторы, резисторы, диоды и транзисторы.
Что такое конденсатор?
Прибор, который накапливает электроэнергию в виде электрических зарядов, называется конденсатором.
Количество электричества или электрический заряд в физике измеряют в кулонах (Кл). Электрическую ёмкость считают в фарадах (Ф).
Уединенный проводник электроёмкостью в 1 фараду – металлический шар с радиусом, равным 13 радиусам Солнца. Поэтому конденсатор включает в себя минимум 2 проводника, которые разделяет диэлектрик. В простых конструкциях прибора – бумага.

Работа конденсатора в цепи постоянного тока осуществляется при включении и выключении питания.Только в переходные моменты меняется потенциал на обкладках.
Конденсатор в цепи переменного тока перезаряжается с частотой, равной частоте напряжения источника питания. В результате непрерывных зарядов и разрядов ток проходит через элемент. Выше частота – быстрее перезаряжается прибор.
Сопротивление цепи с конденсатором зависит от частоты тока. При нулевой частоте постоянного тока величина сопротивления стремится к бесконечности. С увеличением частоты переменного тока сопротивление уменьшается.
Где применяются конденсаторы?
Работа электронных, радиотехнических и электрических устройств невозможна без конденсаторов.
В электротехнике прибор используется для сдвига фаз при запуске асинхронных двигателей. Без сдвига фаз трехфазный асинхронный двигатель в переменной однофазной сети не функционирует.
Конденсаторы с ёмкостью в несколько фарад – ионисторы, используются в электромобилях, как источники питания двигателя.

Для понимания, зачем нужен конденсатор, нужно знать, что 10-12% измерительных устройств работают по принципу изменения электрической ёмкости при изменении параметров внешней среды. Реакция ёмкости специальных приборов используется для:
- регистрации слабых перемещений через увеличение или уменьшение расстояния между обкладками;
- определения влажности с помощью фиксирования изменений сопротивления диэлектрика;
- измерения уровня жидкости, которая меняет ёмкость элемента при заполнении.
Трудно представить, как конструируют автоматику и релейную защиту без конденсаторов. Некоторые логики защит учитывают кратность перезаряда прибора.
Ёмкостные элементы используются в схемах устройств мобильной связи, радио и телевизионной техники. Конденсаторы применяют в:
- усилителях высоких и низких частот;
- блоках питания;
- частотных фильтрах;
- усилителях звука;
- процессорах и других микросхемах.

Легко найти ответ на вопрос, для чего нужен конденсатор, если посмотреть на электрические схемы электронных устройств.
Принцип работы
В цепи постоянного тока положительные заряды собираются на одной пластине, отрицательные – на другой. За счет взаимного притяжения частицы удерживаются в приборе, а диэлектрик между ними не дает соединиться. Тоньше диэлектрик – крепче связаны заряды.
Конденсатор берет нужное для заполнения ёмкости количество электричества, и ток прекращается.
При постоянном напряжении в цепи элемент удерживает заряд до выключения питания. После чего разряжается через нагрузки в цепи.
Переменный ток через конденсатор движется иначе. Первая ¼ периода колебания – момент заряда прибора. Амплитуда зарядного тока уменьшается по экспоненте, и к концу четверти снижается до нуля. ЭДС в этот момент достигает амплитуды.
Во второй ¼ периода ЭДС падает, и элемент начинает разряжаться. Снижение ЭДС вначале небольшое и ток разряда, соответственно, тоже. Он нарастает по той же экспоненциальной зависимости. К концу периода ЭДС равна нулю, ток – амплитудному значению.
В третьей ¼ периода колебания ЭДС меняет направление, переходит через нуль и увеличивается. Знак заряда на обкладках изменяется на противоположный. Ток уменьшается по величине и сохраняет направление. В этот момент электрический ток опережает по фазе напряжение на 90°.
В катушках индуктивности происходит наоборот: напряжение опережает ток. Это свойство стоит на первом месте при выборе, какие цепи использовать в схеме: RC или RL.
В завершении цикла при последней ¼ колебания ЭДС падает до нуля, а ток достигает амплитудного значения.
«Ёмкость» разряжается и заряжается по 2 раза за период и проводит переменный ток.
Это теоретическое описание процессов. Чтобы понять, как работает элемент в цепи непосредственно в устройстве, рассчитывают индуктивное и емкостное сопротивление цепи, параметры остальных участников, и учитывают влияние внешней среды.
Характеристики и свойства

К параметрам конденсатора, которые используют для создания и ремонта электронных устройств, относят:
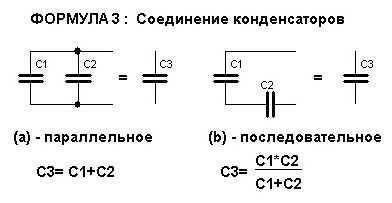
- Ёмкость – С. Определяет количество заряда, которое удерживает прибор. На корпусе указывается значение номинальной ёмкости. Для создания требуемых значений элементы включают в цепь параллельно или последовательно. Эксплуатационные величины не совпадают с расчетными.
- Резонансная частота – fр. Если частота тока больше резонансной, то проявляются индуктивные свойства элемента. Это затрудняет работу. Чтобы обеспечить расчетную мощность в цепи, конденсатор разумно использовать на частотах меньше резонансных значений.
- Номинальное напряжение – Uн. Для предупреждения пробоя элемента рабочее напряжение устанавливают меньше номинального. Параметр указывается на корпусе конденсатора.
- Полярность. При неверном подключении произойдет пробой и выход из строя.
- Электрическое сопротивление изоляции – Rd. Определяет ток утечки прибора. В устройствах детали располагаются близко друг к другу. При высоком токе утечки возможны паразитные связи в цепях. Это приводит к неисправностям. Ток утечки ухудшает емкостные свойства элемента.
- Температурный коэффициент – TKE. Значение определяет, как ёмкость прибора меняется при колебаниях температуры среды. Параметр используют, когда разрабатывают устройства для эксплуатации в тяжелых климатических условиях.
- Паразитный пьезоэффект. Некоторые типы конденсаторов при деформации создают шумы в устройствах.
Виды конденсаторов
Емкостные элементы классифицируют по типу диэлектрика, применяемого в конструкции.
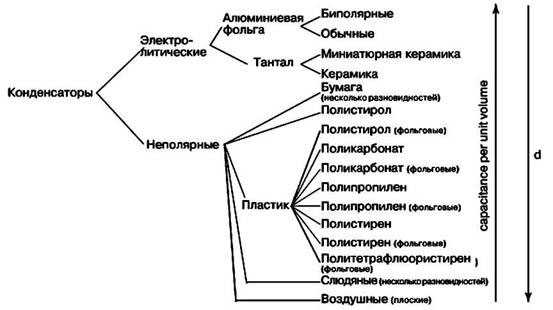
Бумажные и металлобумажные конденсаторы
Элементы используются в цепях с постоянным или слабо пульсирующим напряжением. Простота конструкции оборачивается пониженной на 10-25% стабильностью характеристик и возросшей величиной потерь.
В бумажных конденсаторах обкладки из алюминиевой фольги разделяет бумага. Сборки скручивают и помещают в корпус в форме цилиндра или прямоугольного параллелепипеда.
Приборы работают при температурах -60…+125°C, с номинальным напряжением у низковольтных приборов до 1600 В, высоковольтных – выше 1600 В и ёмкостью до десятков мкФ.
В металлобумажных приборах вместо фольги на диэлектрическую бумагу наносят тонкий слой металла. Это помогает изготовить элементы меньших размеров. При незначительных пробоях возможно самовосстановление диэлектрика. Металлобумажные элементы уступают бумажным по сопротивлению изоляции.
Электролитические конденсаторы
Конструкция изделий напоминает бумажные. Но при изготовлении электролитических элементов бумагу пропитывают оксидами металлов.
В изделиях с электролитом без бумаги оксид наносится на металлический электрод. У оксидов металлов односторонняя проводимость, что делает прибор полярным.
В некоторых моделях электролитических элементов обкладки изготавливают с канавками, которые увеличивают площадь поверхности электрода. Зазоры в пространстве между пластинами устраняют с помощью заливания электролитом. Это улучшает емкостные свойства изделия.
Большая ёмкость электролитических приборов – сотни мкФ, используется в фильтрах, чтобы сглаживать пульсации напряжения.

Алюминиевые электролитические
В приборах этого типа анодная обкладка делается из алюминиевой фольги. Поверхность покрывают оксидом металла – диэлектриком. Катодная обкладка – твердый или жидкий электролит, который подбирается так, чтобы при работе восстанавливался слой оксида на фольге. Самовосстановление диэлектрика продлевает время работы элемента.
Конденсаторы такой конструкции требуют соблюдения полярности. При обратном включении разорвет корпус.
Приборы, внутри которых располагаются встречно-последовательные полярные сборки, используют в 2 направлениях. Ёмкость алюминиевых электролитических элементов достигает нескольких тысяч мкФ.

Танталовые электролитические
Анодный электрод таких приборов изготовляют из пористой структуры, получаемой при нагреве до +2000°C порошка тантала. Материал внешне напоминает губку. Пористость увеличивает площадь поверхности.
С помощью электрохимического окисления на анод наносят слой пентаоксида тантала толщиной до 100 нанометров. Твердый диэлектрик делают из диоксида марганца. Готовую конструкцию прессуют в компаунд – специальную смолу.
Танталовые изделия используют на частотах тока свыше 100 кГц. Ёмкость создается до сотен мкФ, при рабочем напряжении до 75 В.

Полимерные
В конденсаторах используются электролит из твердых полимеров, что дает ряд преимуществ:
- увеличивается срок эксплуатации до 50 тыс. часов;
- сохраняются параметры при нагреве;
- расширяется диапазон допустимых пульсаций тока;
- сопротивление обкладок и выводов не шунтирует ёмкость.

Пленочные
Диэлектрик в этих моделях – пленка из тефлона, полиэстера, фторопласта или полипропилена.
Обкладки – фольга или напыление металлов на пленку. Конструкция используется для создания многослойных сборок с увеличенной площадью поверхности.
Пленочные конденсаторы при миниатюрных размерах обладают ёмкостью в сотни мкФ. В зависимости от размещения слоев и выводов контактов делают аксиальные или радиальные формы изделий.

В некоторых моделях номинальное напряжение 2 кВ и выше.
В чем отличие полярного и неполярного?
Неполярные допускают включение конденсаторов в цепь без учета направления тока. Элементы применяются в фильтрах переменных источников питания, усилителях высокой частоты.
Полярные изделия подсоединяют в соответствии с маркировкой. При включении в обратном направлении прибор выйдет из строя или не будет нормально работать.
Полярные и неполярные конденсаторы большой и малой ёмкости отличаются конструкцией диэлектрика. В электролитических конденсаторах, если оксид наносится на 1 электрод или 1 сторону бумаги, пленки, то элемент будет полярным.
Модели неполярных электролитических конденсаторов, в конструкциях которых оксид металла нанесли симметрично на обе поверхности диэлектрика, включают в цепи с переменным током.
У полярных на корпусе присутствует маркировка положительного или отрицательного электрода.
От чего зависит ёмкость?
Главная функция и роль конденсатора в цепи заключается в накоплении зарядов, а дополнительная – не допускать утечек.
Величина ёмкости конденсатора прямо пропорциональна диэлектрической проницаемости среды и площади пластин, и обратно пропорциональна расстоянию между электродами. Возникает 2 противоречия:
- Чтобы увеличить ёмкость, электроды нужны как можно толще, шире и длиннее. При этом размеры прибора увеличивать нельзя.
- Чтобы удерживать заряды и обеспечить нужную силу притяжения, расстояние между пластинами делают минимальным. При этом ток пробоя уменьшать нельзя.

Для разрешения противоречий разработчики применяют:
- многослойные конструкции пары диэлектрик и электрод;
- пористые структуры анодов;
- замену бумаги на оксиды и электролиты;
- параллельное включение элементов;
- заполнение свободного пространства веществами с повышенной диэлектрической проницаемостью.
Размеры конденсаторов уменьшаются, а характеристики становятся лучше с каждым новым изобретением.
odinelectric.ru
Для чего нужен конденсатор и как он работает
Конденсатор (от латинского слова «condensare» — «уплотнять», «сгущать») — это двухполюсное устройство с определённой величиной или переменным значением ёмкости и малой проводимостью, которое способно сосредотачивать, накапливать и отдавать другим элементам электрической цепи заряд электрического тока.
Конденсатор или как его еще называют сокращенно просто «кондер» — это элемент электрической цепи, состоящий в самом простом варианте из двух электродов в форме пластин (или обкладок), которые накапливают противоположные разряды и поэтому они разделены между собой диэлектриком малой толщины по сравнению с размерами самих электропроводящих обкладок.
Принцип работы конденсатора
По принципу работы он схож с батарейкой только на первый взгляд, но все же он сильно отличается от него по принципу и скорости заряда-разряда, максимальной емкости.
Заряд конденсатора. В момент подключения к источнику питания оказывается больше всего места на электродах, поэтому и ток будет зарядки максимальным, но по мере накопления заряда, ток будет уменьшаться и пропадет полностью после полного заряда. При зарядке на одной пластине будут собираться отрицательно заряженные частицы- электроны, а на другой – ионы, положительно заряженные частицы. Диэлектрик выступает препятствием для их перескакивания на противоположную сторону конденсатора.
Разрядка конденсатора. Если после окончания зарядки отключить источник питания и подключить нагрузку R, то он сам превратится в источник тока. При подключении нагрузки образовывается цепь между пластинами. Отрицательно заряженные электроны двинуться через нагрузку к положительно заряженных ионам на другой пластине по закону притяжения между разноименными зарядами.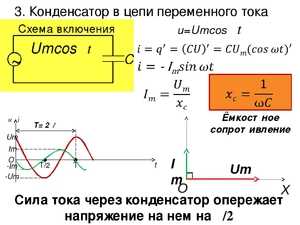
После того как пошел ток, конденсатор начинает постепенно терять заряд или разряжаться. Одновременно с этим начнет снижаться величина напряжения, соответственно по закону Ома и ток. В то же время чем выше уровень разряда обкладок, тем ниже будет скорость падения напряжения и силы тока. Процесс завершится после того, как напряжение на электродах конденсатора станет равно нулю.
Время зарядки конденсатора на прямую зависит от величины его емкости. Чем большей она величины, тем дольше будет проходить по цепи большее количество заряда.
Время разрядки зависит от величины подключенной нагрузки. Чем больше подключено сопротивление R, тем меньше будет ток разрядки.
Для чего нужен конденсатор
Конденсаторы широко используются во всех электронных и радиотехнических схемах. Они вместе с транзисторами и резисторами являются основой радиотехники.
Применение конденсаторов в электротехнических устройствах и бытовой технике:
- Важным свойством конденсатора в цепи переменного тока является его способность выступать в роли емкостного сопротивления (индуктивное у катушки). Если подключить последовательно конденсатор и лампочку к батарейке, то она не будет светиться. Но если подключить к источнику переменного тока, то она загорится. И светиться будет тем ярче, чем выше емкость конденсатора. Благодаря этому свойству они широко применяются в качестве фильтра, который способен довольно успешно подавлять ВЧ и НЧ помехи, пульсации напряжения и скачки переменного тока.
- Благодаря способности конденсаторов долгое время накапливать заряд
- Способность конденсатора накапливать и сохранять электрический заряд на продолжительное время, сделало возможным использование его в элементах для сохранения информации. А так же в качестве источника питания для маломощных устройств. Например, пробника электрика, который достаточно вставить в розетку на пару секунд пока не зарядится в нем встроенный конденсатор и затем можно целый день прозванивать цепи с его помощью. Но к сожалению, конденсатор значительно уступает в способности накапливать электроэнергию аккумуляторной батареи из-за токов утечки (саморазряда) и неспособности накопить электроэнергию большой величины.
- Конденсаторы используются при подключении электродвигателя 380 на 220 Вольт. Он подключается к третьему выводу, и благодаря тому что он сдвигает фазу на 90 градусов на третьем выводе- становится возможным использования трехфазного мотора в однофазной сети 220 Вольт.
- В промышленности конденсаторные установки применяются для компенсации реактивной энергии.
В следующей статье мы рассмотрим подробно основные характеристики и типы конденсаторов.
jelektro.ru
Конденсатор в цепи переменного тока
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной. Она определяется исключительно самим конденсатором, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость С конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением U нельзя так поступить! Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.

Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения. Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения . Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с тригонометрическим кругом, на нем все это видно очень наглядно.
Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов. Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости C конденсатора, амплитуды приложенного к нему напряжения Um и частоты ω. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).

Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t) через конденсатор емкостью C. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото )

Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует . Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.
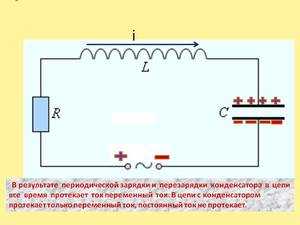
Рисунок 4 – График напряжения в розетке

Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
myelectronix.ru
Конденсатор в цепи переменного тока
Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.
Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).
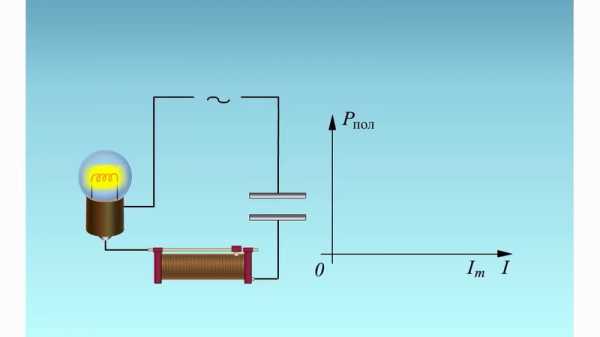
Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.
В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.
Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.
С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.
Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.
Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.
В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.
Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны
Емкостное сопротивление конденсатора
Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС
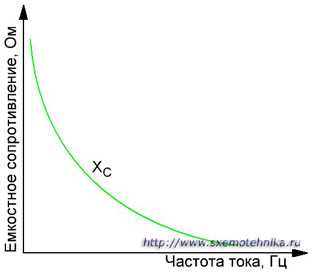
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.

Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.
Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.
Величина емкостного сопротивления определяется по следующей формуле:
где Хс — емкостное сопротивление конденсатора в ом;
f—частота переменного тока в гц;
ω — угловая частота переменного тока;
С — емкость конденсатора в ф.
При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.
Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.
Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.
Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.
Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.
Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.
Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.
Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.
Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.
В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.
В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.
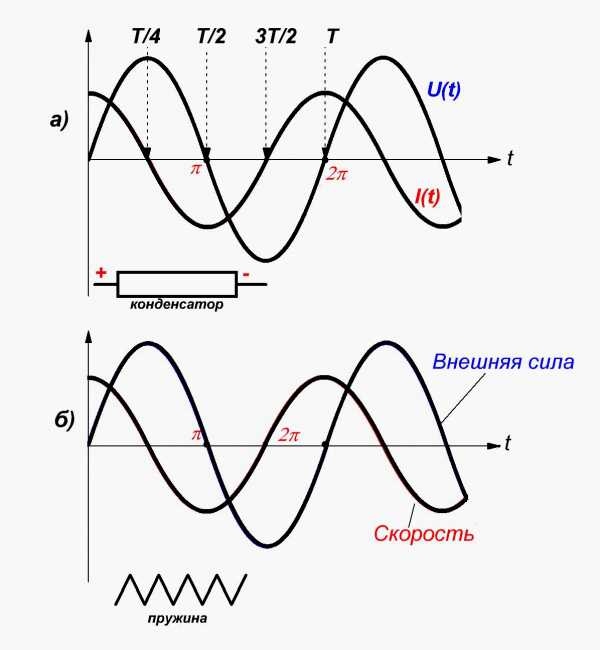
Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.

Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.
Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.
Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.
И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.
При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.
А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Конденсатор в цепи постоянного и переменного тока
Главная страница ➟ Электрика и электроника info ➞ Конденсатор ➞ Конденсатор в цепи постоянного и переменного тока
Конденсатор в цепи постоянного и переменного тока ведет себя абсолютно по разному.
Помните, что такое конденсатор? Давайте-ка я вам напомню. Конденсатор, он же в народе «кондёр», состоит из двух изолированных обкладок. При кратковременной подаче на конденсатор постоянного напряжения, он заряжается и сохраняет в себе этот заряд. Емкость конденсатора зависит от того, на сколько «мест» рассчитаны обкладки, а также смотря, какое расстояние между ними. Давайте рассмотрим простейшую схему уже заряженного кондера:
Итак, мы здесь видим на одной обкладке восемь «плюсов», а на другой столько же и «минусов». Ну а как вы знаете, противоположности притягиваются) И чем меньше расстояние между обкладками, тем сильнее «любовь. Следовательно, плюс «любит» минус, а так как любовь взаимная, значит и минус тоже «любит» плюс)). Поэтому, это притяжение не дает разрядиться уже заряженному конденсатору.
Для того, чтобы разрядить конденсатор, достаточно проложить «мостик», чтобы «плюсы» и «минусы» встретились. То есть тупо замкнуть два вывода от прокладок хорошим проводником. Конденсаторы большой емкости лучше разряжать черезсопротивление, то есть резистором.
С кондером вроде разобрались… А вот что такое «цепь» ?
Бывают велосипедные цепи, мотоциклетные, цепи для бензопилы, а бывают еще так называемые «электрические цепи». То есть это провода, лампочки, говорилки, радиодетали и тд соединенные в какой то последовательности и через которые идет или будет идти электрический ток от источника питания. Да хотя бы даже от батарейки или Блока питания.
Думаю, вы знаете, что электрический ток бывает переменным и постоянным. Давайте же узнаем, как ведет себя конденсатор, когда через него проходит постоянный и переменный ток?
Конденсатор в цепи постоянного тока
Итак, берем блок питания постоянного напряжения и выставляем на его крокодилах напряжение в 12 Вольт. Лампочку тоже берем на 12 Вольт. Теперь между одним щупом блока питания и лампочки вставляем конденсатор:
Не-а, не горит.
А вот если напрямую сделать, то горит:
Отсюда напрашивается вывод: постоянный ток через конденсатор не течет!
Ну не, если честно, то в самый начальный момент подачи напряжения ток все-таки течет на доли секунды. Все зависит от емкости конденсатора. Но это в расчет не берут.
Конденсатор в цепи переменного тока
Итак, чтобы узнать, течет ли переменный ток через конденсатор, нам нужен генератор переменного тока. Думаю, этот генератор частоты вполне сойдет:
Так как китайский генератор у меня очень слабенький, то мы вместо нагрузки-лампочки будем использовать простой Резистор на 100 Ом. Также возьмем и конденсатор емкостью в 1 микроФарад:
Спаиваем как-то вот так и подаем сигнал с генератора частоты:
Далее за дело берется Цифровой осциллограф OWON SDS6062. Что такое осциллограф и с чем его едят, читаем здесь. Будем использовать сразу два канала, ну то есть на одном экране будут высвечиваться сразу два сигнала. Здесь на экранчике уже видны наводки от сети 220 Вольт. Не обращайте внимание.
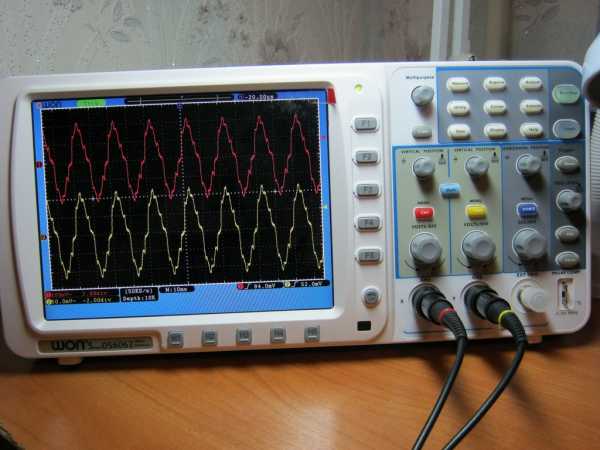
Будем подавать переменное напряжение и смотреть сигналы, как говорят профессиональные электронщики, на входе и на выходе. Одновременно.
Все это будет выглядеть примерно вот так:
Итак, если у нас частота нулевая, то это значит постоянный ток. Постоянный ток, как мы уже видели, конденсатор не пропускает. С этим вроде бы разобрались. Но что будет, если подать синусоиду с частотой в 100 Герц?
На дисплее осциллографа я вывел такие параметры, как частота сигнала и его амплитуда: F — это частота, Ma — амплитуда (эти параметры пометил белой стрелочкой). Первый канал помечен красным цветом, а второй канал — желтым, для удобства восприятия.
Красная синусоида показывает сигнал, который выдает нам китайский генератор частоты. Желтая синусоида — это то, что мы уже получаем на нагрузке. В нашем случае нагрузкой является резистор. Ну вот, собственно, и все.
Как вы видите на осциллограмме выше, с генератора я подаю синусоидальный сигнал с частотой в 100 Герц и амплитудой в 2 Вольта. На резисторе мы уже видим сигнал с такой же частотой (желтый сигнал), но его амплитуда составляет каких-то 136 миллиВольт. Да еще и сигнал получился какой-то «лохматый». Это связано с так называемыми «шумами». Шум — это по идее сигнал с маленькой амплитудой и беспорядочным изменением напряжения, ловимый из окружающей среды. Также радиоэлементы тоже могут добавлять шум. Например очень хорошо «шумит» резистор. Значит «лохматость» сигнала — это сумма синусоиды и шума.
Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается влево, то есть опережает красный сигнал, или научным языком, появляется сдвиг фаз. Опережает именно фаза, а не сам сигнал. Если бы опережал сам сигнал, то у нас бы тогда получилось, что сигнал на резисторе появлялся бы по времени раньше, чем сигнал, поданый на него через конденсатор. Получилось бы какое-те перемещение во времени :-), что конечно же, невозможно.
Сдвиг фаз — это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:
Давайте увеличим частоту на генераторе до 500 Герц
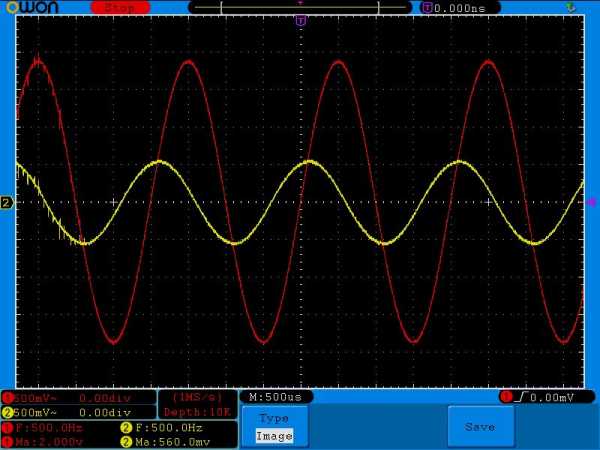
На резисторе уже получили 560 миллиВольта. Сдвиг фаз уменьшается.
Увеличиваем частоту до 1 КилоГерца
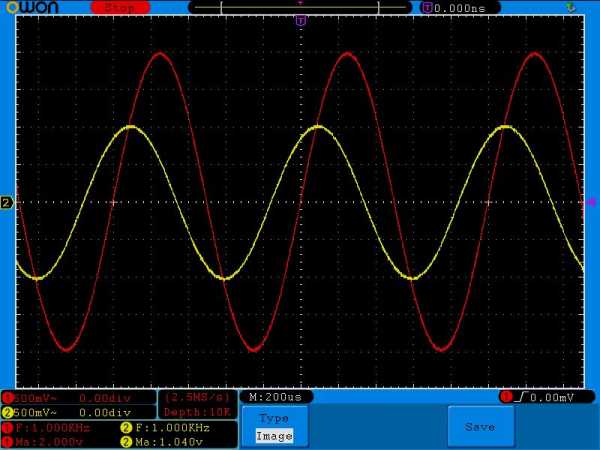
На выходе у нас уже 1 Вольт.
Ставим частоту 5 КилоГерц
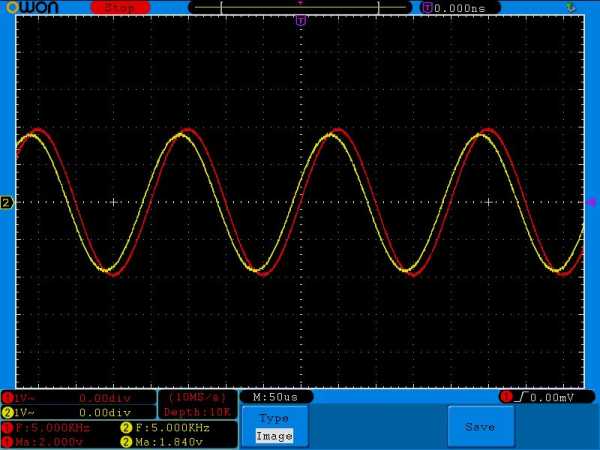
Амплитуда 1,84 Вольта и сдвиг фаз явно стает меньше
Увеличиваем до 10 КилоГерц
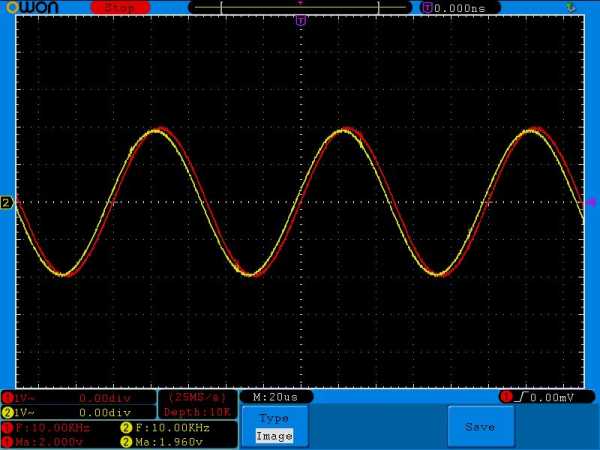
Амплитуда уже почти такая же как и на входе. Сдвиг фаз менее заметен.
Ставим 100 КилоГерц:
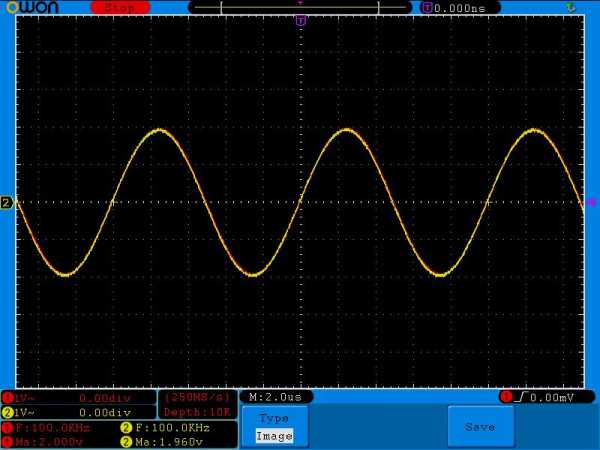
Сдвига фаз почти нет. Амплитуда почти такая же, как и на входе, то есть 2 Вольта.
Отсюда делаем глубокомысленные выводы:
Чем больше частота, тем меньшее сопротивление конденсатор оказывает переменному току. Сдвиг фаз убывает с увеличением частоты почти до нуля. На бесконечно низких частотах его величина составляет 90 градусов или π/2.
Если построить обрезок графика, то получится типа что-то этого:
По вертикали я отложил напряжение, по горизонтали — частоту.
Итак, мы с вами узнали, что сопротивление конденсатора зависит от частоты. Но только ли от частоты? Давайте возьмем конденсатор емкостью в 0,1 микроФарад, то есть номиналом в 10 раз меньше, чем предыдущий и снова прогоним по этим же частотам.
Смотрим и анализируем значения:
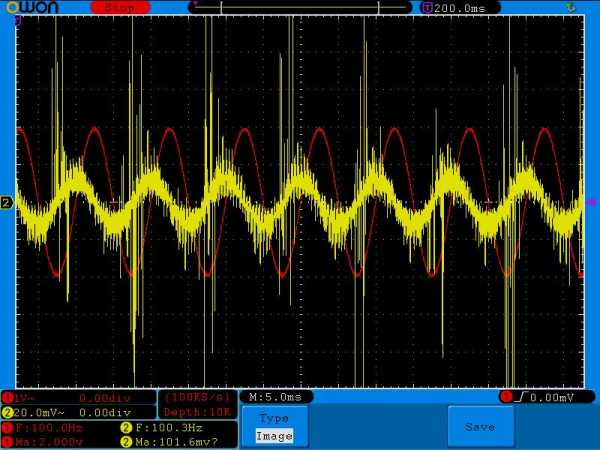
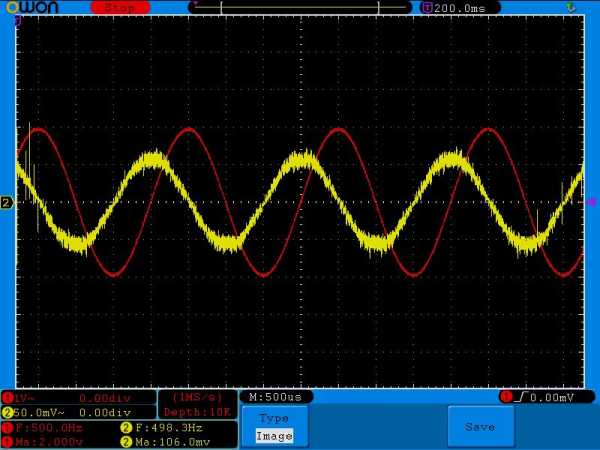
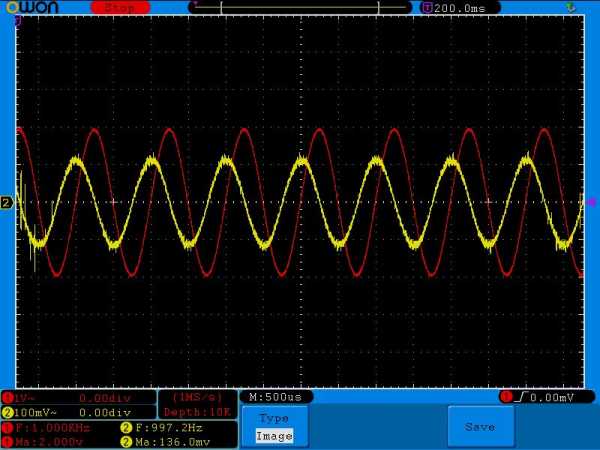
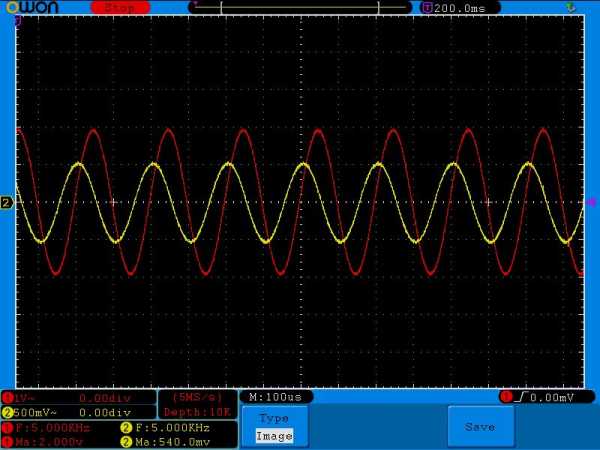
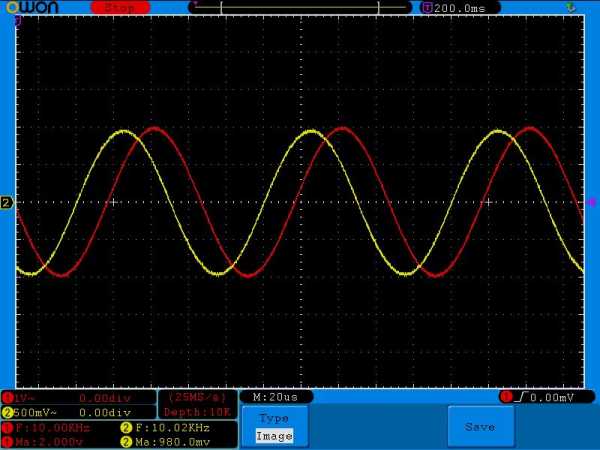
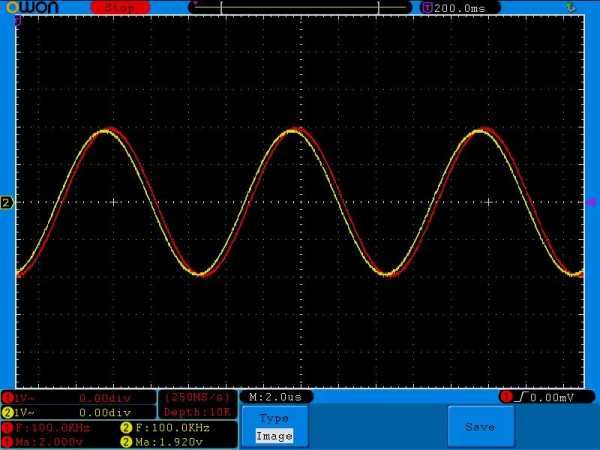
Внимательно сравните амплитудные значения желтого сигнала на одной и той же частоте, но с разными номиналми конденсатора. Например, на частоте в 100 Герц и номиналом кондера в 1 мкФ амплитуда желтого сигнала равнялась 136 миллиВольт, а на этой же самой частоте амплитуда желтого сигнала, но с кондером в 0,1 мкФ уже была 101 миллиВольт( в реальности еще меньше из за помех). На частоте 500 Герц — 560 миллиВольт и 106 миллиВольт соответственно, на частоте в 1 КилоГерц — 1 Вольт и 136 миллиВольт и так далее.
Отсюда вывод напрашивается сам собой: при уменьшении номинала конденсатора его сопротивление стает больше.
С помощью физико-математических преобразований физики и математики вывели формулу для расчета сопротивления конденсатора. Прошу любить и жаловать:
где, ХС — это сопротивление конденсатора, Ом
П — постоянная и равняется приблизительно 3,14
F — частота, измеряется в Герцах
С — емкость, измеряется в Фарадах
Так вот, поставьте в эту формулу частоту в ноль Герц. Частота в ноль Герц — это и есть постоянный ток. Что получится? 1/0=бесконечость или очень большое сопротивление. Короче говоря, обрыв цепи.
Забегая вперед, могу сказать, что в данном опыте мы получили Фильтр Высокой Частоты (ФВЧ). С помощью простого конденсатора и резистора, применив где-нибудь в звуковой аппаратуре такой фильтр на динамик, в динамике мы будет слышать только писклявые высокие тона. А вот частоту баса как раз и заглушит такой фильтр. Зависимость сопротивления конденсатора от частоты очень широко используется в радиоэлектронике, особенно в различных фильтрах, где надо погасить одну частоту и пропустить другую.
Источник информации:
https://www.ruselectronic.com/kondensator-v-tsepi-peremennogo-toka/#more-160
kudashkin.com
