Прямая / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Прямая
Если отрезок АВ продолжить в обе стороны, то получим геометрическую фигуру, которая называется прямая.
Обозначается и произносится: прямая АВ (или прямая ВА).
Про точки А и В говорят, что они лежат на прямой (принадлежат прямой).
Отрезок АВ лежит на прямой АВ.
Через любые две точки на плоскости проходит единственная прямая (одна и только одна прямая).
На рисунке также изображена прямая АВ (точки не отмечены).
Часто прямые обозначают одной строчной буквой латинского алфавита ( .., m, n,…):
.., m, n,…):
Читают: прямая m, прямая n.
Прямая не имеет начала и не имеет конца.
Пересекающиеся прямыеНа рисунке прямые a и b имеют одну общую точку О. Говорят, что прямые a и b пересекаются в точке О.
Сами прямые называются пересекающимися (a и b – пересекающиеся прямые).
Любые две пересекающиеся прямые имеют только одну общую точку.
Перпендикулярные прямыеДве прямые называются перпендикулярными
На чертежах такой угол отмечают значком прямого угла «».
Для обозначения перпендикулярных прямых используют знак перпендикулярности «⏊«.
Записывают: с⏊d;
Читают: прямая с перпендикулярна прямой d.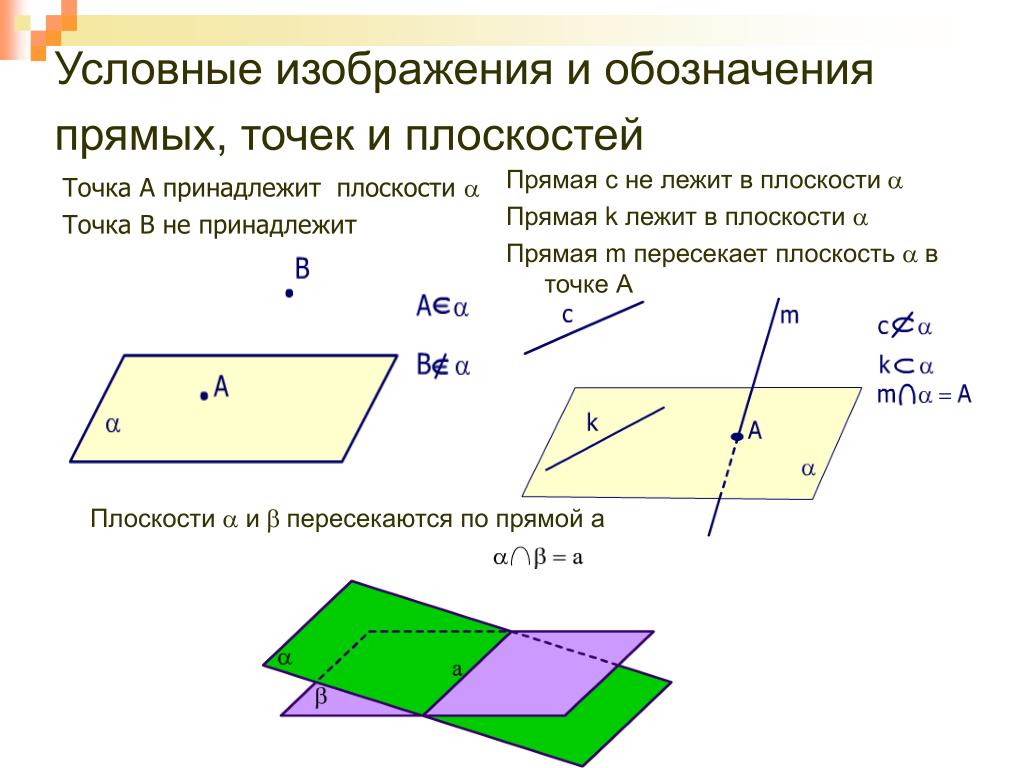
Перпендикулярные прямые называют взаимно перпендикулярными, потому, что верны выражения «прямые c и d перпендикулярны» или «прямые d и с перпендикулярны».
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 79, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1622, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1662, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 3, Мерзляк, Полонский, Якир, Учебник
Упражнение 7, Мерзляк, Полонский, Якир, Учебник
Упражнение 86, Мерзляк, Полонский, Якир, Учебник
Упражнение 90, Мерзляк, Полонский, Якир, Учебник
Упражнение 99, Мерзляк, Полонский, Якир, Учебник
Упражнение 103, Мерзляк, Полонский, Якир, Учебник
Упражнение 379, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 512, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 585, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1397, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1422, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1543, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1544, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5.
Пользовательское соглашение
Copyright
Обозначение пересекающихся прямых. Прямая в математике. Прямая на плоскости
Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.
 А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.
А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.
В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена.
Что такое точка в математике?
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
В последнем случае эти буквы указывают концы отрезка.
Страница 1 из 3
§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.
Вопрос 3. Как обозначаются точки и прямые?
Ответ. Точки обозначаются прописными латинскими буквами: A, B, C, D, … . Прямые обозначаются строчными латинскими буквами: a, b, c, d, … .
Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую a на рисунке 4 можно обозначить AC, а прямую b можно обозначить BC.
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
Ответ. Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.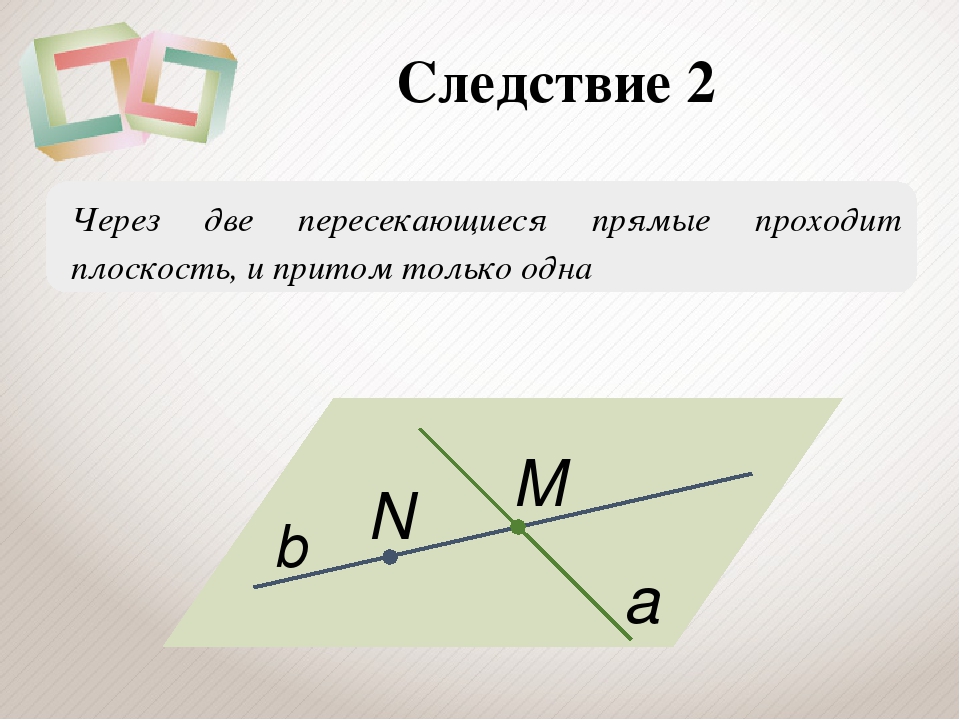
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.
Навигация по странице.
Прямая на плоскости — понятие.
Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости .
Теперь можно переходить и к понятию прямой линии на плоскости .
Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
Взаимное расположение прямой и точки.
Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.
Точки принято обозначать большими латинскими буквами, например, точки А
и F
. В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a
и d
.
В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a
и d
.
Возможны два варианта взаимного расположения прямой и точки на плоскости : либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А лежит на прямой а , то можно записать . Если точка А не принадлежит прямой а , то записывают .
Справедливо следующее утверждение: через любые две точки проходит единственная прямая.
Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А
и В
), можно обозначать двумя этими буквами (в нашем случае прямая АВ
или ВА
).
Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком . Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А и В являются концами отрезка, тогда этот отрезок можно обозначить АВ или ВА . Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и .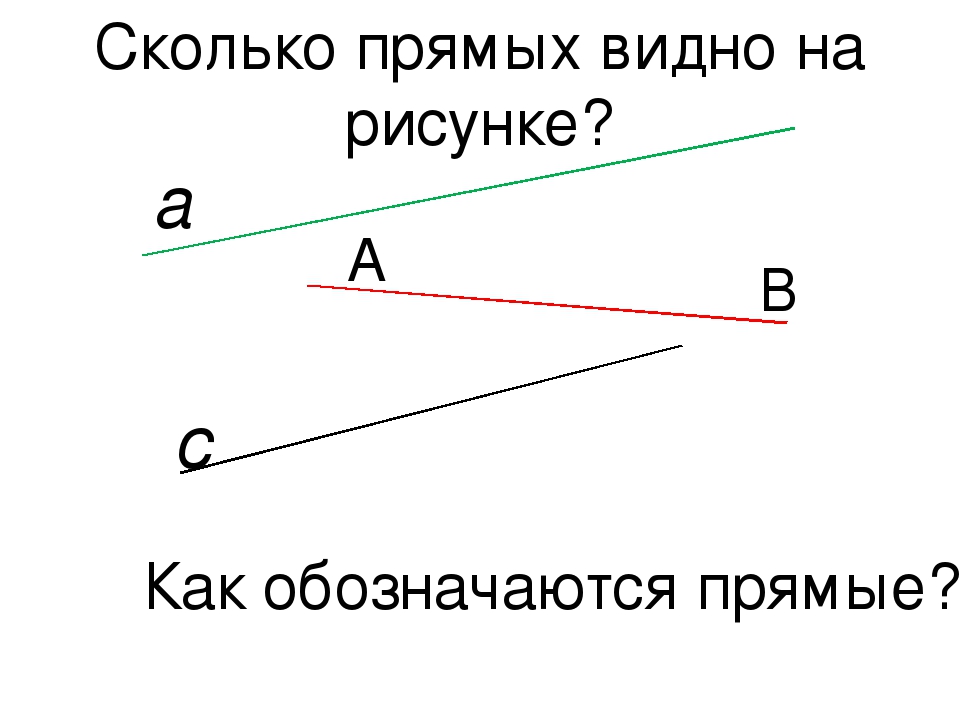 Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ
принадлежит прямой а
, можно кратко записать .
Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ
принадлежит прямой а
, можно кратко записать .
Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А , В и С лежат на одной прямой, причем точка В лежит между точками А и С . Тогда можно говорить, что точки А и С находятся по разные стороны от точки В . Также можно сказать, что точки В и С лежат по одну сторону то точки А , а точки А и В лежат по одну сторону от точки С .
Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча . Для этого случая дается аксиома: произвольная точка О
, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О
, а две любые точки разных лучей – по разные стороны от точки О
.
Взаимное расположение прямых на плоскости.
Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?
Во-первых, две прямые на плоскости могут совпадать .
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
Во-вторых, две прямые на плоскости могут пересекаться .
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «», к примеру, запись означает, что прямые а
и b
пересекаются в точке М
. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми . Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a
перпендикулярна прямой b
, то можно использовать краткую запись .
Если прямая a
перпендикулярна прямой b
, то можно использовать краткую запись .
В-третьих, две прямые на плоскости могут быть параллельными.
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой . В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой . О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости .
Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются.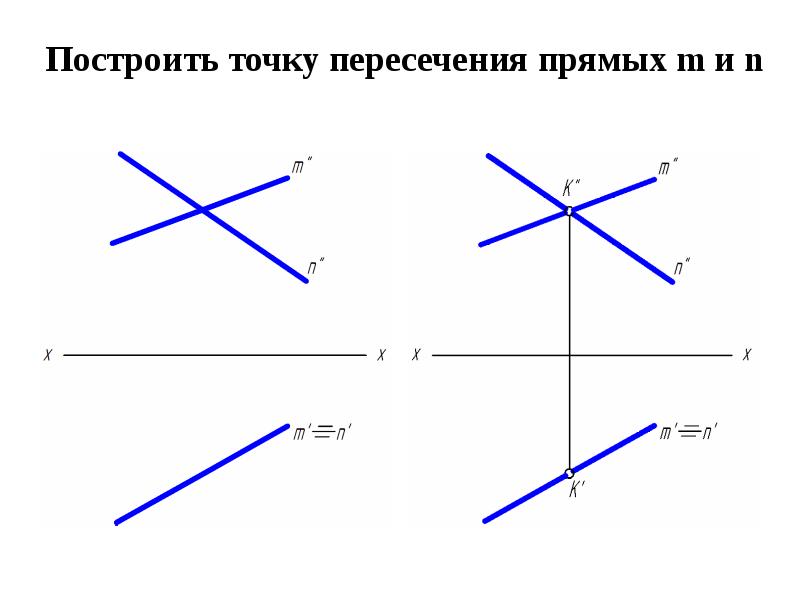 При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:
- если две прямые параллельны третьей прямой, то они параллельны между собой;
- если две прямые перпендикулярны третьей прямой, то они параллельны между собой;
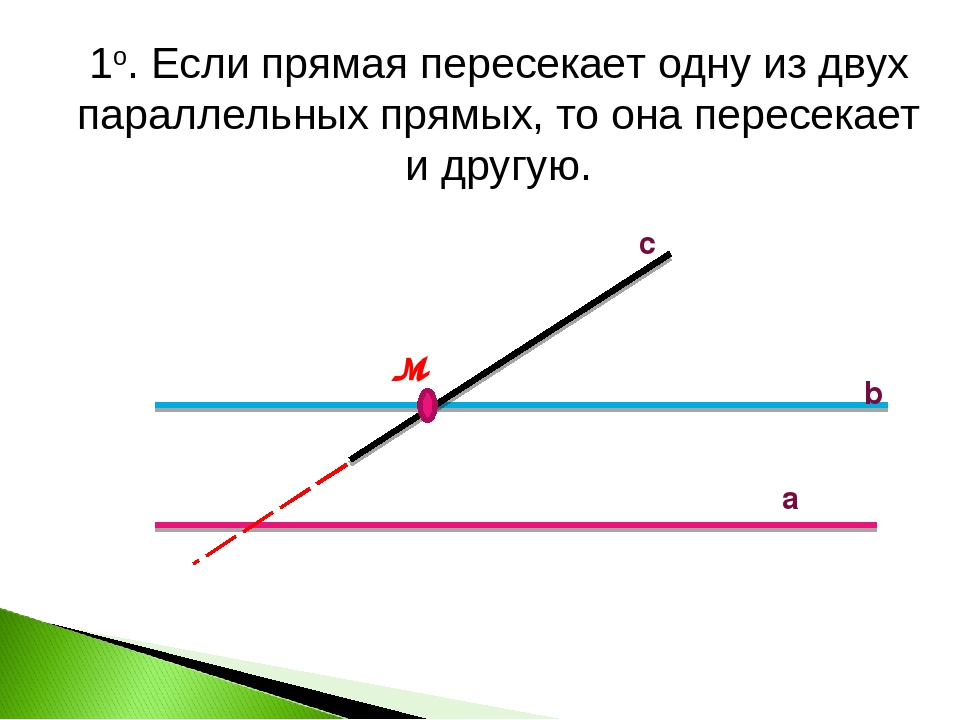
- если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.
Способы задания прямой на плоскости.
Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.
Во-первых, прямую можно задать, указав две точки на плоскости.
Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.
Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки .
Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.
Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой .
В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.
Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости .
Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.
Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.
Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой .
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.

- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину.
 Ширины и толщины она не имеет
Ширины и толщины она не имеетОбозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.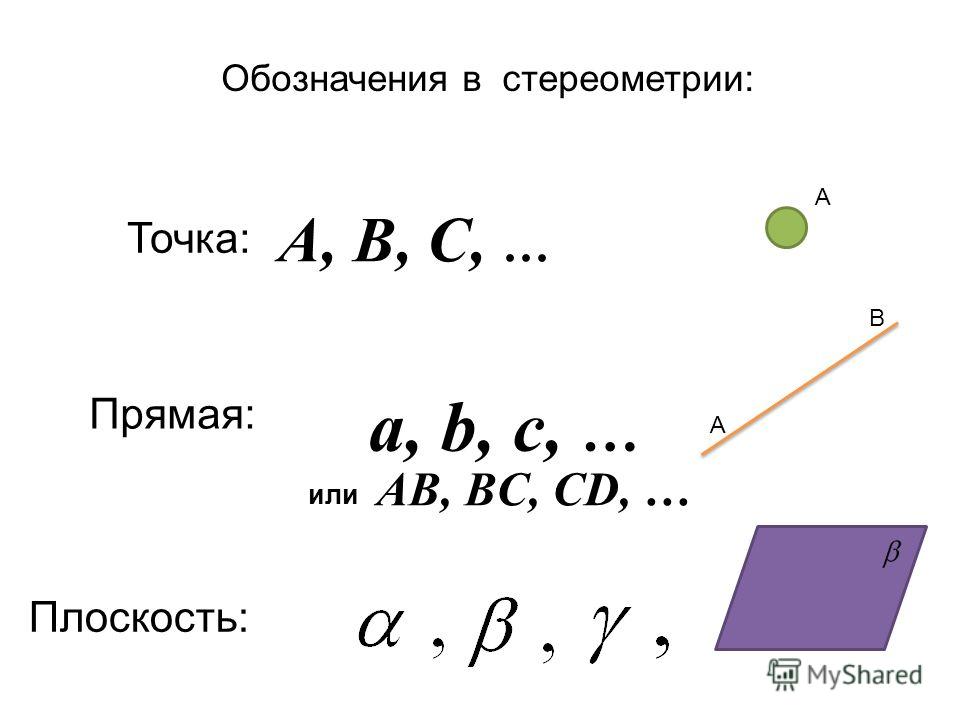
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.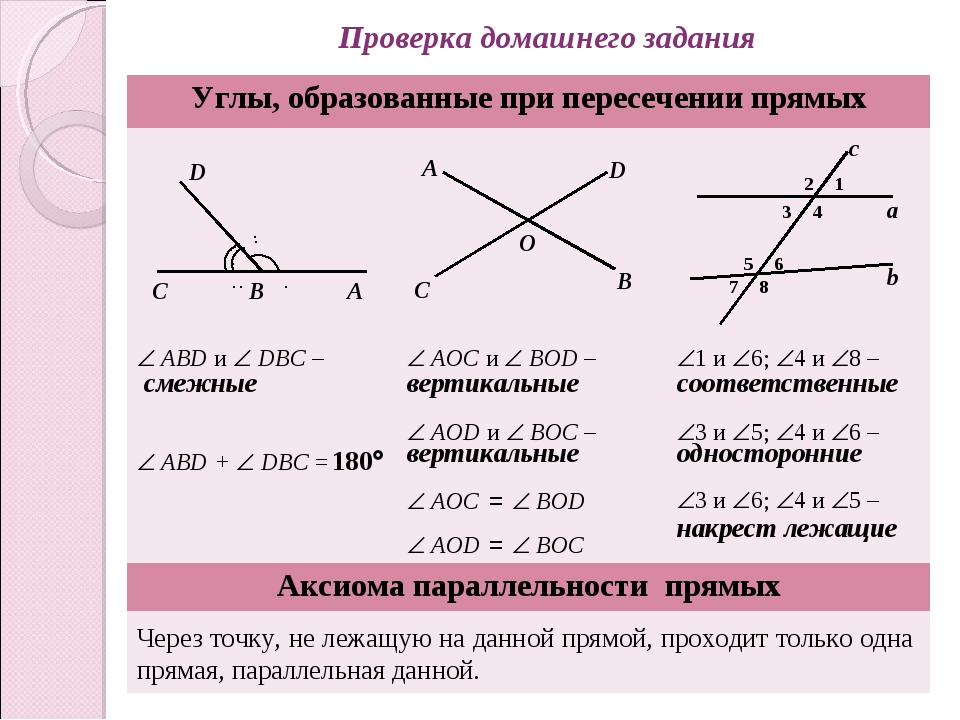 д.
д.
| Аксиомы стереометрии и их следствия Аксиома 2. Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. Аксиома 3. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. Некоторые следствия из аксиомТеорема 2. |
Признак параллельности двух плоскостей Теорема. |
Свойства параллельных плоскостей
Вели α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Параллельные, пересекающиеся, скрещивающиеся прямые в пространстве.
Параллельные прямые: если две прямые в пространстве параллельны друг другу, то на комплексном чертеже их все одноименные проекции также параллельны.
Пересекающиеся прямые: если две прямые в пространстве пересекаются, то на комплексном чертеже их одноименные проекции пересекаются, и точки пересечения этих проекций лежат на одной линии связи.
Скрещивающиеся прямые: если две прямые в пространстве не параллельны и не пересекаются, то они скрещиваются. На комплексном чертеже одноименные проекции могут пересекаться, но точки их пересечения не будут лежать на одной линии связи.
Изображение точки на прямой (ее принадлежность)
Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскостей проекций. Если точка в пространстве принадлежит прямой, то ее проекции должны лежать на одноименных проекциях этой прямой.
10. Пололожение скрещивающихся прямых положено в основу метода конкурирующих точек, который используется для определения видимости геометрических элементов (рис. 26):
1) Чтобы определить видимость в горизонтальной проекции конкурирующих точек двух скрещивающихся прямых m и n, необходимо через точку пересечения горизонтальных проекций этих прямых (11≡21) провести линию связи до фронтальных проекций этих же прямых. Найденные точки 12и 22будут являться
фронтальными проекциями конкурирующих точек. Видимой будет та точка, которая расположена
выше, т.е. больше высота (в данном случае – точка 1).
2) Чтобы определить видимость во фронтальной проекции конкурирующих точек двух скрещивающихся прямых m и n, необходимо через точку пересечения горизонтальных проекций этих прямых (32≡42) провести линию связи до горизонтальных проекций этих же прямых.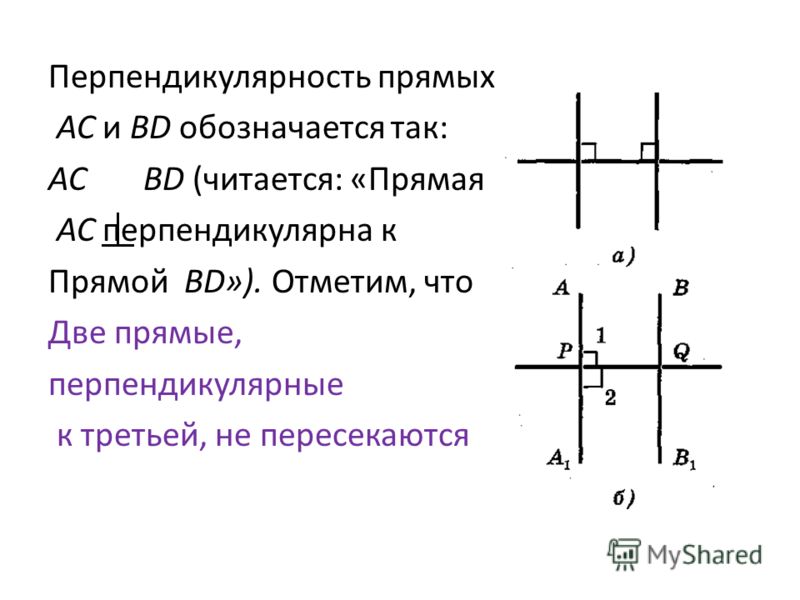 Полученные точки 31 и 41
Полученные точки 31 и 41
будут являться горизонтальными Рис. 26
проекциями конкурирующих точек. Видимой будет та точка, которая расположена дальше от плоскости П2, т.е. больше глубина (в данном случае – точка 4).
11.Плоскостью называется поверхность, образуемая движением прямой линии параллельно самой себе по неподвижной направляющей прямой.
На чертеже плоскость может быть задана следующими способами:
1) Любой плоской фигурой
2) Тремя точками, не принадлежащими одной прямой
3) Прямой и точкой вне ее
4) Двумя параллельными прямыми
5) Двумя пересекающимися прямыми
6) Следами плоскости
12. Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций, т.е. со всеми плоскостями проекций составляет произвольные углы.
13.Проецирующая плоскость –плоскость, которая перпендикулярна одной из плоскостей , выражается на ней в прямую линию ,совпадающую со следами проецирующих плоскостей . С другими плоскостями проекций образует произвольные углы.
С другими плоскостями проекций образует произвольные углы.
14.(а)Фронтально-проецирующая плоскостьперпендикулярна плоскости проекции V .Проецирующая на данную плоскость проекций в прямую линию. С плоскостями проекций Hи Wплоскость образует произвольные углы.
а б в
(б)Горизонтально-проецирующая плоскостьперпендикулярна плоскости проекцийН.Проецируется на данную плоскость проекций в прямую линию . С плоскостями проекций WиVплоскость образует произвольные углы.
(в)Профильно-проецирующая плоскость перпендикулярна плоскости проекцииW . Проецирующая на данную плоскость проекций в прямую линию. С плоскостями проекций Hи V имеет произвольные углы.
15.Плоскость уровня-плоскость ,параллельная одной из основных плоскостей проекций и перпендикулярна двум другим плоскостям .
16.Фронтальная плоскость уровня– плоскость, параллельная плоскости проекции V и перпендикулярна H и W.
Горизонтальная плоскость уровня- плоскость, параллельная плоскости проекции H и перпендикулярна V и W.
Профильная плоскость уровня- плоскость, параллельная плоскости проекции W и перпендикулярна H и V.
17. Следы плоскости- прямые, по которым плоскость пересекается с плоскостями проекций. След плоскости обозначают заглавной буквой, которая принята для обозначения самой плоскости, с буквенным индексом внизу (например , Pv, P h, Pw) . Виды следов: Pv – фронтальный след плоскости Р; Ph – горизонтальный след; Pw – профильный след.
19) 1.вид сверху (главный вид)V
2.вид сверху(под видом впереди)H
3. вид слева (справа от главного вида)W
4.вид справа(слева от главного вида)W1
5.вид снизу(над главным видом)h2
6. вид сзади(справа от вида слева или слева от вида справа)V1
вид сзади(справа от вида слева или слева от вида справа)V1
20) Если же виды сверху, слева и справа не находятся в проекционной связи с главным изображением, то они отмечаются на чертеже надписью по типу «А». Направление взгляда указывается стрелкой, обозначаемой прописной буквой русского алфавита.
21)Разрезом называется изображение предмета, мысленно рассеченного одной или несколькимисекущимиплоскостями. Hа pазpезе показывают то, что расположено в секущей плоскости и что расположено за ней.
22. Какие вы знаете разрезы?
Рассмотрим простые разрезы.
Фронтальный разрез — изображение, полученное в результате мысленного рассечения детали секущей плоскостью, параллельной фронтальной плоскости проекций, и состоящее из фигу- ры сечения и изображения части детали, расположенной за секущей плоскостью.
Деталь помещают в систему плоскостей проекций (V, H или V, H, W) и мысленно рассекают секущей плоскостью, параллельной фронтальной плоскости проекций. Фигуру сечения и то, что расположено за секущей Плоскостью, проецируют на плоскость V, получая изображение фронтального разреза (рис. 155).
Фигуру сечения и то, что расположено за секущей Плоскостью, проецируют на плоскость V, получая изображение фронтального разреза (рис. 155).
Профильным разрезом называется изображение, полученное при мысленном рассечении детали секущей плоскостью, параллельной профильной плоскости проекций, и состоящее из фигуры сечения и изображения части детали, расположенной за ней.
Деталь помешают в систему плоскостей проекций (V, H или V, H, W) и мысленно рассекают секущей плоскостью, параллельной профильной плоскости проекций. Фигуру сечения и то, что расположено за секущей плоскостью, проецируют на плоскость W, получая изображение профильного разреза (рис. 156).
Горизонтальный разрез — изображение, полученное при мысленном рассечении детали секущей плоскостью параллельной горизонтальной плоскости проекций, и состоящее из фигуры сечения и изображения части детали, расположенной за секущей плоскостью.
Рассмотрим сложные разрезы.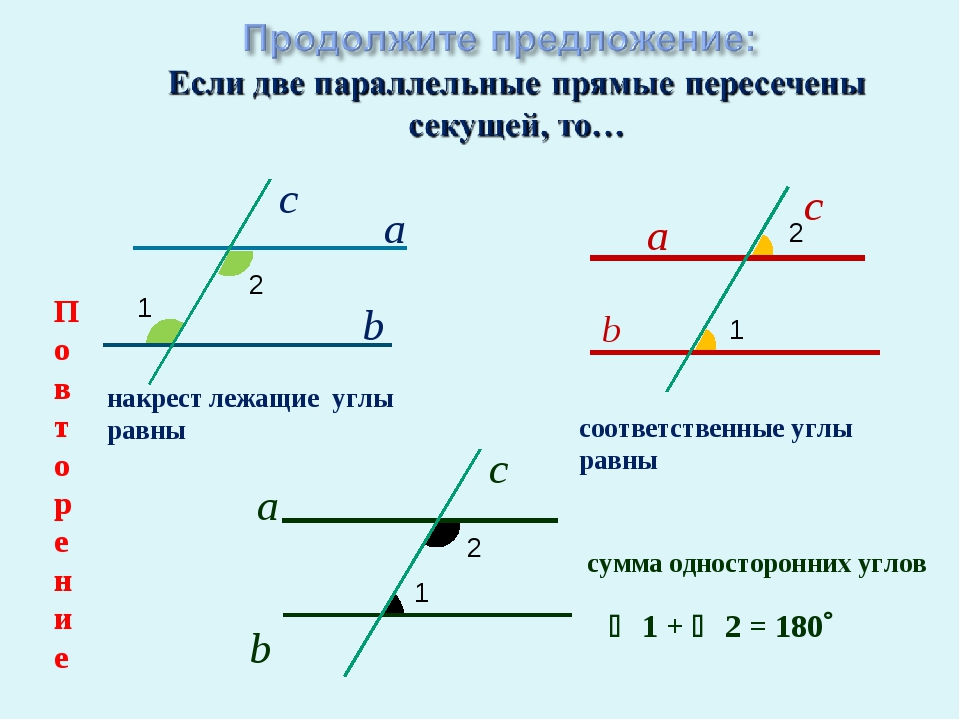
Ступенчатым называется сложный разрез, образованный двумя и более секущими параллельными плоскостями. Ступенчатые разрезы могут быть фронтальными, профильными и горизонтальными.
Ломаным разрезом называется сложный разрез, образованный двумя пересекающимися плоскостями. На разрезах тонкие стенки, ребра жесткости, спицы показывают не заштрихованными, если секущая плоскость проходит вдоль оси или длинной стороны элемента детали.
23.Как обозначаются разрезы
Разрезы на чертеже, как правило, обозначаются. Однако есть случаи, когда обозначение разреза не наносится. Рассмотрим правила обозначения разрезов:
1. Если секущая плоскость совпадает с плоскостью симметрии детали, то разрез на чертеже не обозначается
2. Если секущая плоскость не совпадает с плоскостью симметрии детали, то разрез обозначается следующим образом. Положение секущей плоскости показывают штрихами разомкнутой линии. К штрихам разомкнутой линии на расстоянии 2-3 мм от внешнего края ставят стрелки, указывающие направление взгляда (рис. 180). С внешней стороны стрелок пишут прописные буквы русского алфавита. Изображение разреза подписывается надписью типа А-А, Б-Б (рис. 180).
180). С внешней стороны стрелок пишут прописные буквы русского алфавита. Изображение разреза подписывается надписью типа А-А, Б-Б (рис. 180).
24. Какая разница между разрезом и сечением
Отличие разреза от сечения
Сразу же стоит выделить, что разрез от сечения отличается не только правилом построения, как путают многие люди, имеющие дело непосредственно с чертежами. Признаков отличия несколько, и некоторые из них весьма существенные:
· Главное отличие кроется в том, что разрез показывает то, что расположено в секущей плоскости, а также за ней, в то время сечение показывает то, что внутри секущей плоскости.
· В некоторых случаях обозначение разреза не наносится на чертеж. Например, при совпадении секущей плоскости с плоскостью симметрии детали.
· Сечение имеет несколько нюансов при построении. Например, если несколько одинаковых сечений относятся к одному и тому же предмету, то его линии необходимо обозначать одинаковыми буквами. При этом вычеркивается одно сечение. Данное правило довольно часто не соблюдается, хотя является довольно важным при построении чертежа.
Данное правило довольно часто не соблюдается, хотя является довольно важным при построении чертежа.
Несмотря на то, что разрез и сечения имеют очень много общего, TheDifference.ru определил, что разница между ними есть. Сечение и разрез отличают друг от друга по следующим признакам:
1. Правило построения.
2. Разрез показывает расположение как в секущей плоскости, так и вне нее. Сечение же только то, что внутри.
3. Сечения необходимы для показа поперечной формы деталей. Предмет мысленно рассекается одной или несколькими плоскостями. Сечение обозначается штриховкой для более ясного понимания.
4. Разрез в отдельных случаях можно не наносить на чертеж.
25. Как обозначаются сечения на чертежах?
сечение – это изображение фигуры, получающейся в одной или нескольких секущих плоскостях при мысленном рассечении предмета. Сечение – это составная часть каждого разреза. В сечении показывается только то, что получается непосредственно в самой секущей плоскости , а на разрезе ещё и то, что нах-ся за секущей плоскостью.
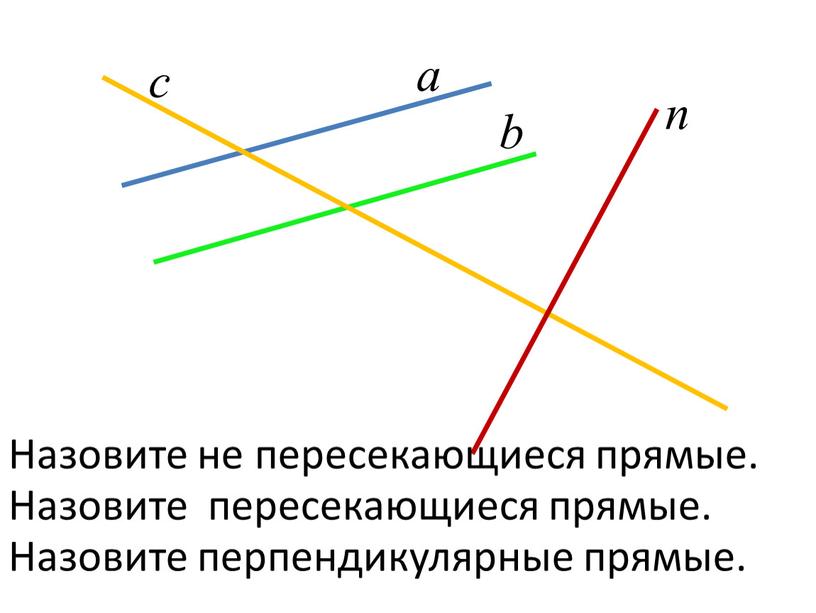
Прямые: пересекающиеся и параллельные
Если две прямые в пространстве имеют общую точку, то говорят, что эти две прямые пересекаются. На следующем рисунке, прямые a иb пересекаются в точке A. Прямые а и с не пересекаются.
рисунок
Любые, две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Параллельные прямые
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и при этом не пересекаются. Для обозначения параллельных прямых используют специальный значок — ||.
Запись a||b означает, что прямая а параллельна прямой b. На рисунке представленном выше, прямые а и с параллельны.
Теорема о параллельных прямых
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной и притом только одна.
Скрещивающиеся прямые
Две прямые, которые лежат в одной плоскости, могут либо пересекаться либо быть параллельными. Но в пространстве две прямые не обязательно должны принадлежать оной плоскости. Они могут быть расположены в двух разных плоскостях.
Но в пространстве две прямые не обязательно должны принадлежать оной плоскости. Они могут быть расположены в двух разных плоскостях.
Очевидно, что прямые расположенные в разных плоскостях не пересекаются и не являются параллельными прямыми. Две прямые, которые не лежат в одной плоскости, называются скрещивающими прямыми.
На следующем рисунке показаны две скрещивающиеся прямые a и b, которые лежат в разных плоскостях.
рисунок
Признак и теорема о скрещивающихся прямых
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Теорема о скрещивающихся прямых: через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Таким образом, мы рассмотрели все возможные случаи взаимного расположения прямых в пространстве. Их всего три.
1. Прямые пересекаются. (То есть они имеют лишь одну общую точку. )
)
2. Прямые параллельны. (То есть они не имеют общих точек и лежат в одной плоскости.)
3. Прямые скрещиваются. (То есть они расположены в разных плоскостях.)
Нужна помощь в учебе?
Предыдущая тема: Теорема синусов: доказательство и задача для примера
Следующая тема:   Теорема о трех перпендикулярах и обратная ей теорема
Начертательная геометрия. Теория.
Краткий курс начертательной геометрии
Лекции предназначены для студентов инженерно–технических специальностей
Введение
Тема 1. Проецирование точки
Тема 2. Проецирование прямой
Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой
Тема 4. Плоскость. Способы задания плоскостей
Тема 5. Положение плоскости. Следы плоскости
Тема 6. Взаимное положение прямой и плоскости
Тема 7. Взаимное положение плоскостей
Тема 8. Плоскопараллельное перемещение. Вращение.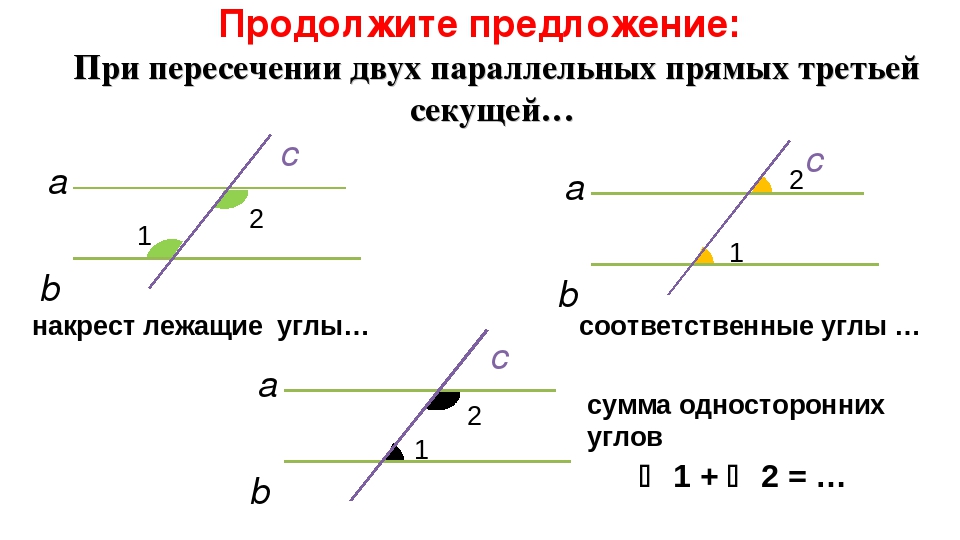 Замена плоскостей проекций
Замена плоскостей проекций
Начертательная геометрия входит в состав учебной дисциплины федерального значения, название которой в зависимости от специальности: «Начертательная геометрия и инженерная графика», «Инженерная и машинная графика» или просто «Инженерная графика». Инженерная графика – это единственная дисциплина целью, которой является непосредственно обучение студентов работе с различной по виду и содержанию графической информацией, основам графического представления информации, методам графического моделирования геометрических объектов, правилам разработки и оформления конструкторской документации, графических моделей явлений и процессов.
Тема 1. Проецирование точки
Если информацию о расстоянии точки относительно плоскости проекции дать не
с помощью числовой отметки, а с помощью второй проекции точки, построенной
на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.
Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод — метод ортогонального проецирования, причем берутся
две проекции на две взаимно перпендикулярные плоскости проекций, — обеспечивая
выразительность, точность и удобоизмеримость изображений предметов на
плоскости, был и остается основным методом составления технических чертежей
Рисунок 1.1 Точка в системе трех плоскостей проекций
Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной.
Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3.
Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0.
Три плоскости проекций делят пространство на восемь трехгранных углов — октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте.
Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают.
Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).
Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте.
Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают.
Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).
К началу страницы
Тема 2. Проецирование прямой
Для определения положения прямой в пространстве существуют следующие методы:
1.Двумя точками ( А и В ).
Рассмотрим две точки в пространстве А и В (рис.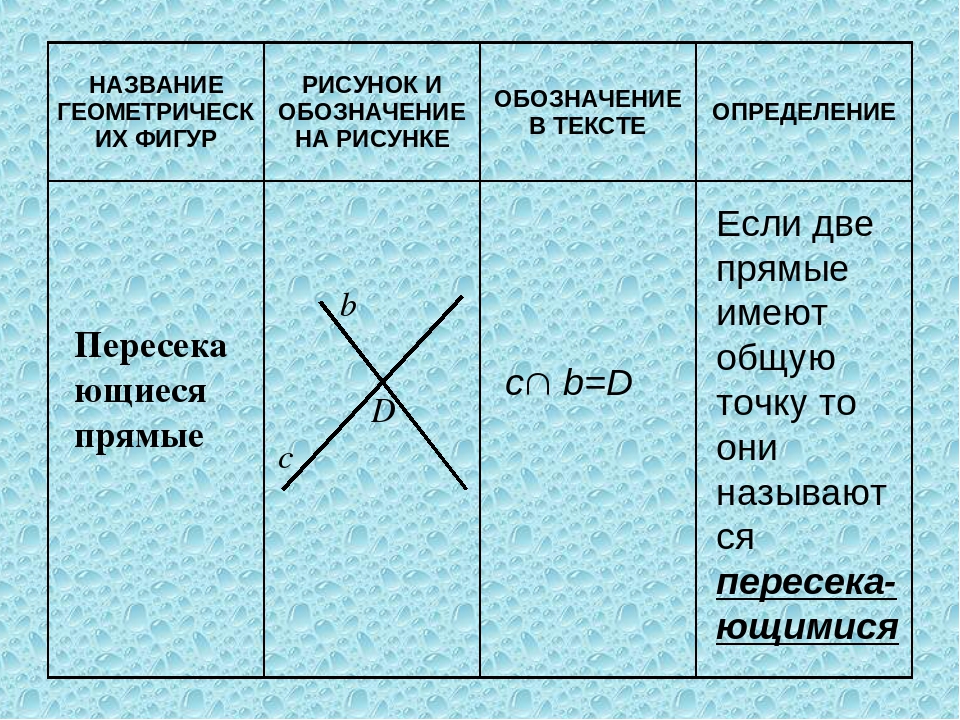 2.1). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].
2.1). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].
Рисунок 2.1 Определение положения прямой по двум точкам
2. Двумя плоскостями (a; b). Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.
К началу страницы
Тема 3. Положение прямой относительно плоскостей проекций.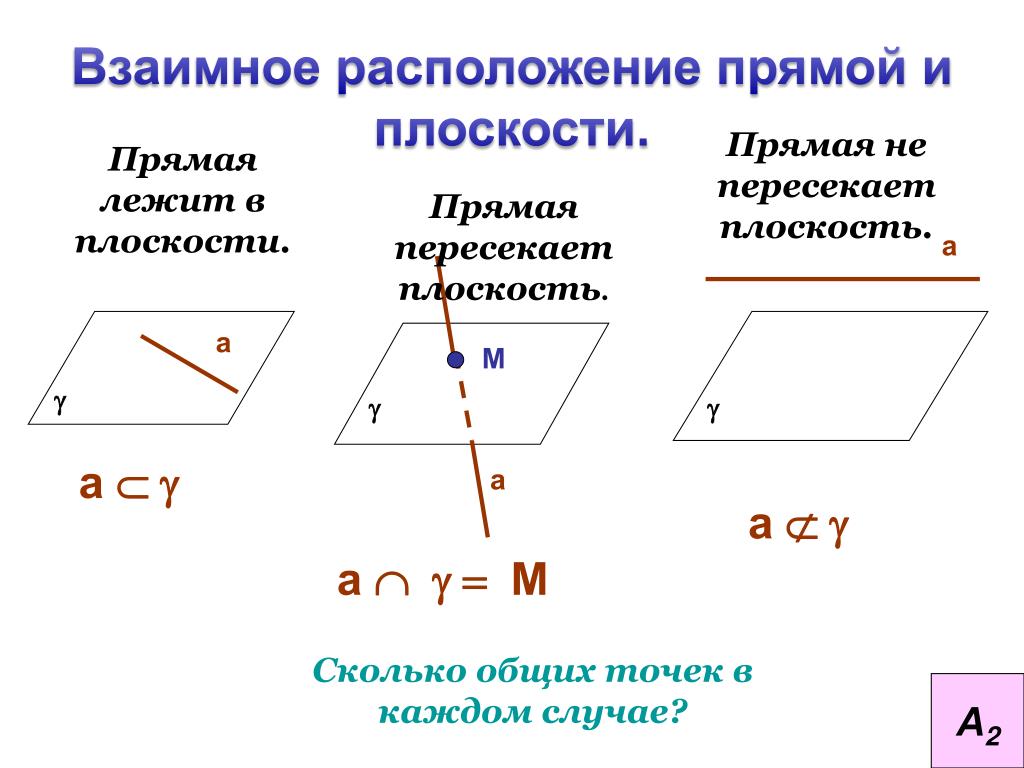 Следы прямой
Следы прямой
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).
Рисунок 3.1 Прямая общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).
Рисунок 3.2 Горизонтальная прямая
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями(рис.3.3).
Рисунок 3.3 Фронтальная прямая
2. 3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).
3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).
Рисунок 3.4 Профильная прямая
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально-проецирующая прямая — АВ (рис. 3.5).
Рисунок 3.5 Фронтально-проецирующая прямая
3.2. Профильно проецирующая прямая — АВ (рис.3.6).
Рисунок 3.6 Профильно-проецирующая прямая
3.3. Горизонтально-проецирующая прямая — АВ (рис.3.7).
Рисунок 3.7 Горизонтально-проецирующая прямая
К началу страницы
Тема 4.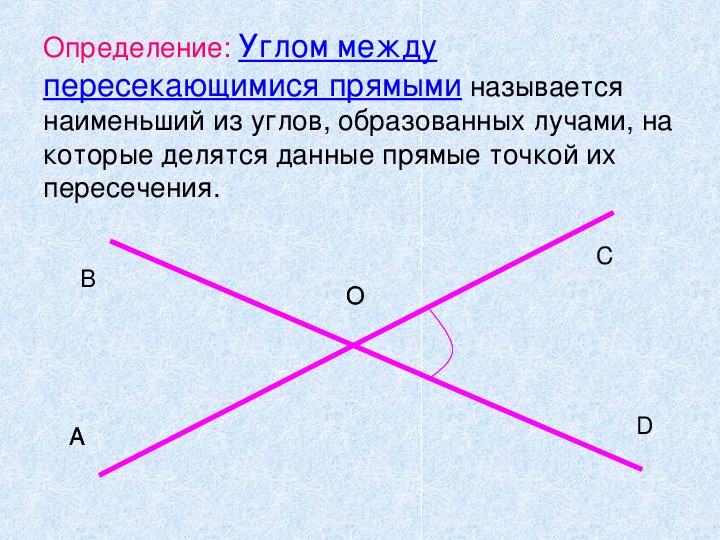 Плоскость. Способы задания плоскостей
Плоскость. Способы задания плоскостей
Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости: 1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки; 2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.
Способы графического задания плоскостей Положение плоскости в пространстве можно определить:
1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).
Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой
2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).
Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии
3. Двумя пересекающимися прямыми (рис.4.3).
Двумя пересекающимися прямыми (рис.4.3).
Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями
4. Двумя параллельными прямыми (рис.4.4).
Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями
Тема 5. Положение плоскости. Следы плоскости
К началу страницы
Различное положение плоскости относительно плоскостей проекций
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: — горизонтальный S1; — фронтальный S2; — профильный S3).
Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az.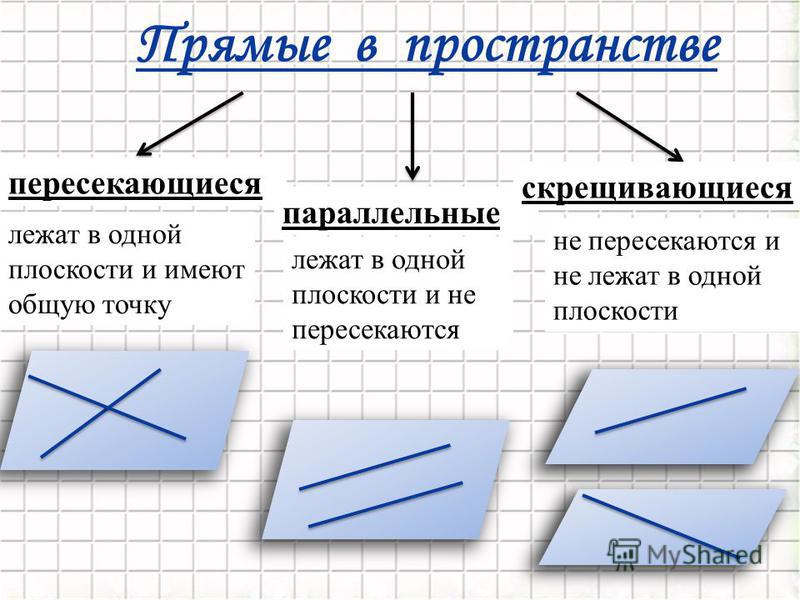 П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые — следы плоскости S1 и S2 (рис.5.7).
П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые — следы плоскости S1 и S2 (рис.5.7).
Рисунок 5.7 Профильная плоскость
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой( как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости S (АВС). Фронтальный след плоскости S2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости S. Горизонтальный следS1 – прямая, проходящая через горизонтальный след прямой АВ и Sx. Профильный следS3 – прямая соединяющая точки (Sy и Sz) пересечения горизонтального и фронтального следов с осями.
Рисунок 5.8 Построение следов плоскости
К началу страницы
Тема 6. Взаимное положение прямой и плоскости, точки и плоскости
Определение взаимного положения прямой и плоскости — позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T(рис.6.1).
Рисунок 6.1 Метод вспомогательных секущих плоскостей
Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости T, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость T. Таким образом возможны три случая относительного расположения прямой и плоскости:
Прямая принадлежит плоскости;
Прямая параллельна плоскости;
Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости.
Рассмотрим каждый случай.
Таким образом возможны три случая относительного расположения прямой и плоскости:
Прямая принадлежит плоскости;
Прямая параллельна плоскости;
Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости.
Рассмотрим каждый случай.
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).
Задача. Дана плоскость (n,k) и одна проекция прямой m2.
Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.
Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k.
Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.
Рисунок 6.2 Прямая и плоскость имеют две общие точки
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).
Задача.
Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k.
Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1.
Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.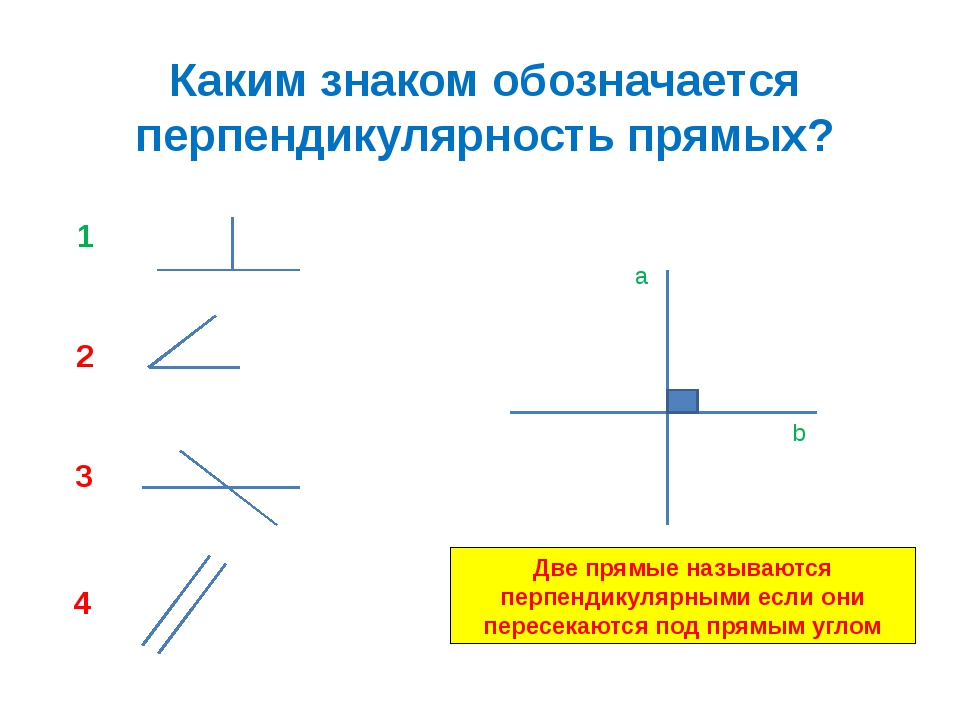
Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h — прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).
Рисунок 6.4 Горизонталь
2. Фронтали f — прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).
Рисунок 6.5 Фронталь
3. Профильные прямые р — прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6).
Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след — это горизонталь плоскости, фронтальный — фронталь и профильный — профильная линия плоскости.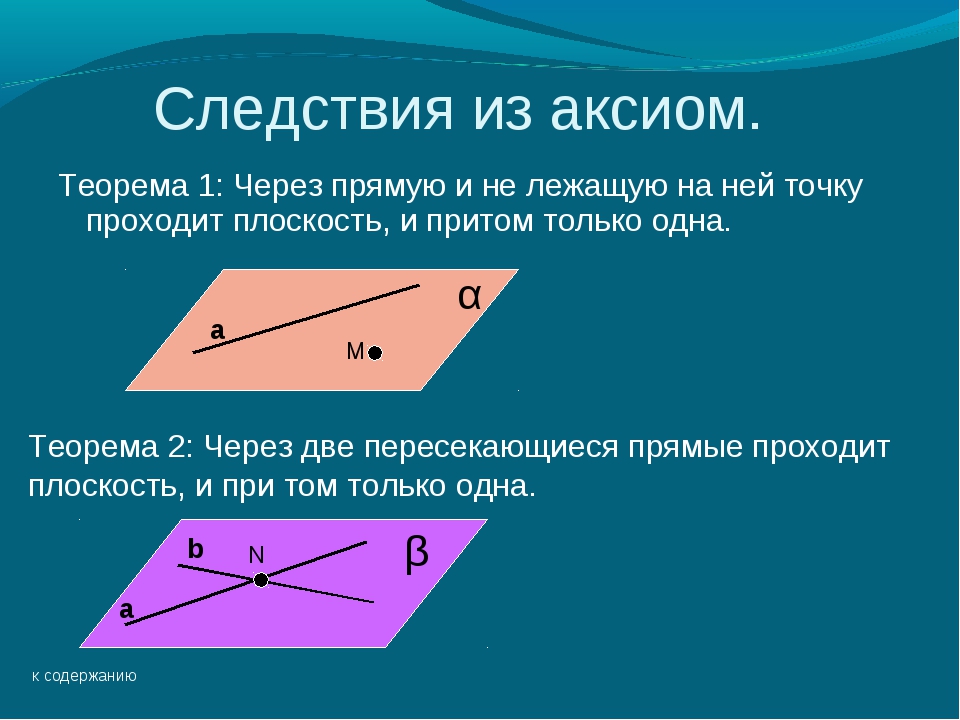
Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.
Рисунок 6.7 Линия наибольшего ската
Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет. Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рис.6.8): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).
Задача. Дано: плоскость T(а,в) и проекция точки А2. Требуется построить проекцию А1 если известно, что точка А лежит в плоскости в,а.
Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2. Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А.
Требуется построить проекцию А1 если известно, что точка А лежит в плоскости в,а.
Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2. Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А.
Рисунок 6.8. Точка, принадлежащая плоскости
К началу страницы
Тема 7. Взаимное положение плоскостей
Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
1. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис. 7.1).
Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В.
Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d.
Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой.
Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования — проекции параллельных прямых — параллельны между собой
d||a, с||b; d1||a1,с1||b1; d2||a2 ,с2||b2; d3||a3,с3||b3.
7.1).
Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В.
Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d.
Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой.
Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования — проекции параллельных прямых — параллельны между собой
d||a, с||b; d1||a1,с1||b1; d2||a2 ,с2||b2; d3||a3,с3||b3.
Рисунок 7.1. Параллельные плоскости
2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей. Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.7.2).
Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.7.2).
Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость — горизонтально проецирующая T. Требуется построить линию пересечения плоскостей. Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью T — точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как T — горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости T1, таким образом остается только построить недостающие проекции [DF] на П2 и П3.
Рисунок 7.2. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью
Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(m,n) и b (ABC) (рис.7.3).
Пусть в пространстве заданы две плоскости общего положения a(m,n) и b (ABC) (рис.7.3).
Рисунок 7.3. Пересечение плоскостей общего положения
Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b — по прямой (34). Точка К — точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b — прямая (КМ).
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.7.4).
Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.7.4).
Рисунок 7.4. Взаимно перпендикулярные плоскости
К началу страницы
Тема 8. Плоскопараллельное перемещение. Вращение. Замена плоскостей проекций
Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 8.1). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.
Рисунок 8.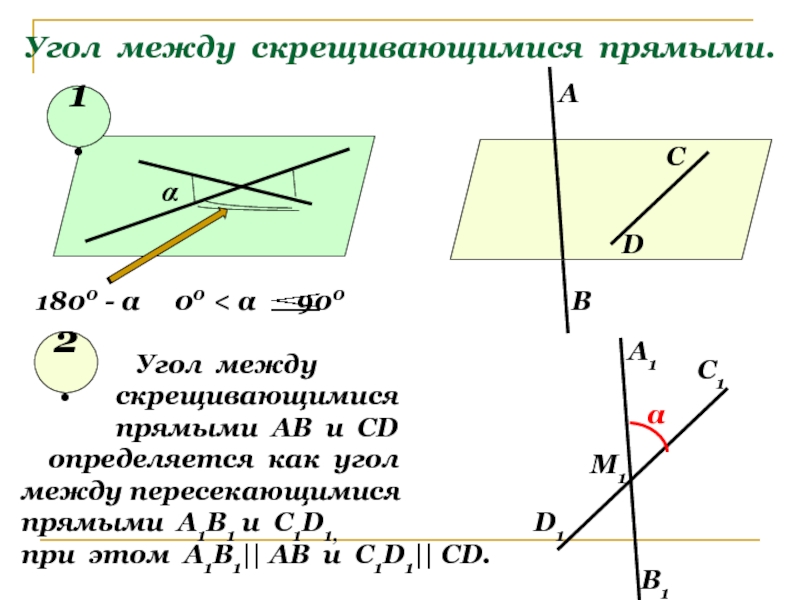 1 Определение натуральной величины отрезка методом плоскопараллельного перемещения
1 Определение натуральной величины отрезка методом плоскопараллельного перемещения
Свойства плоскопараллельного перемещения:
1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.
2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.
Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория — дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 8.2), выберем ось вращения (i) перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А’1, а точка В не изменит своего положения. Положение точки А’2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А’1. Полученная проекция В2 А’2 определяет натуральную величину самого отрезка.
Положение точки А’2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А’1. Полученная проекция В2 А’2 определяет натуральную величину самого отрезка.
Рисунок 8.2 Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций
Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.8.3). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня — горизонтали. Проведем произвольно фронтальную проекцию горизонтали h3 параллельно оси Ох, которая пересекает прямые в точках 12 и 22 . Определив проекции 11 и 11, построим горизонтальную проекцию горизонтали h2 . Траектория движения всех точек при вращении вокруг горизонтали — окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.
Определив проекции 11 и 11, построим горизонтальную проекцию горизонтали h2 . Траектория движения всех точек при вращении вокруг горизонтали — окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.
Рисунок 8.3 Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций
Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности — траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО .Продолжим прямую К1О1 так чтобы |О1К’1|=|КО| . Точка К’1 соответствует точке К , когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь — ось вращения. С учетом этого через точку К’1 и точки 11 и 21 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол фи — натуральная величина угла между прямыми а и в.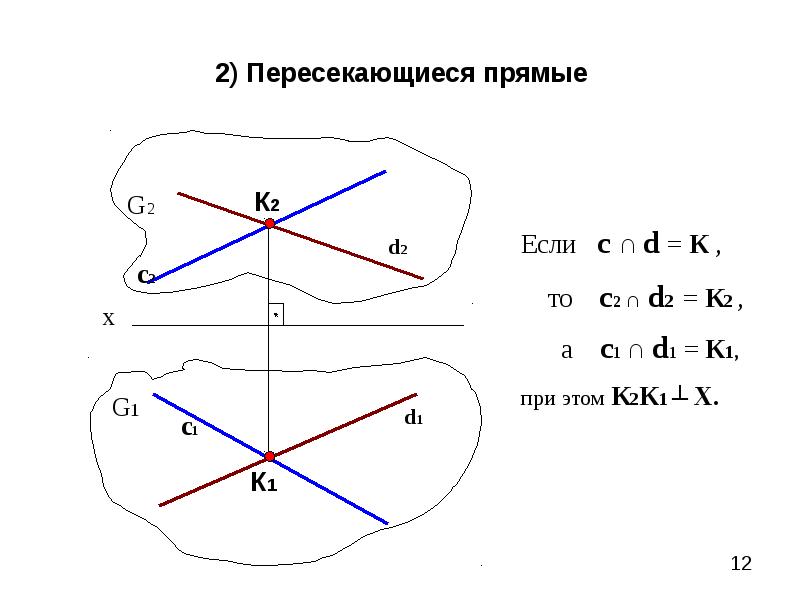
Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 8.4). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4В4 будет натуральной величиной отрезка АВ.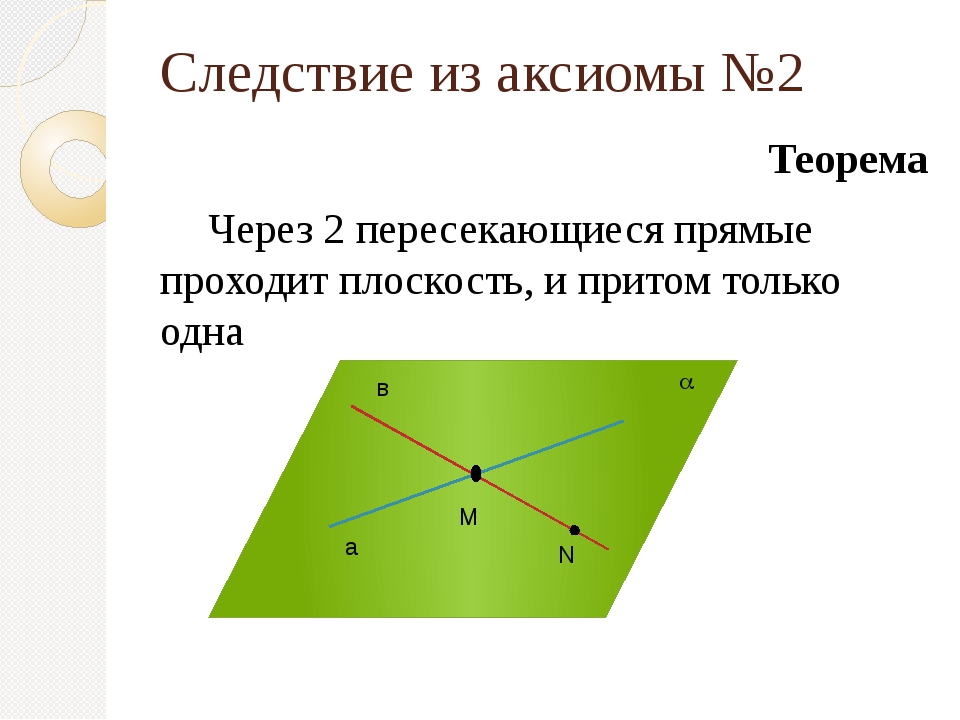
Рисунок 8.4. Определение натуральной величины отрезка прямой методом замены плоскостей проекций
Задача 2: Определить расстояние от точки C до прямой общего положения, заданной отрезком АВ (рис. 8.5).
Рисунок 8.5. Определение натуральной величины отрезка прямой методом замены плоскостей проекций
К началу страницы
Прямая и плоскость /qualihelpy
Простейшими фигурами в пространстве являются точка, прямая и плоскость.
Точки обозначают прописными буквами латинского алфавита: , , , и т. д.Плоскости обозначают строчными буквами греческого алфавита , , и т. д.На рисунках плоскости изображают в виде произвольной области, а чаще в виде параллелограмма.
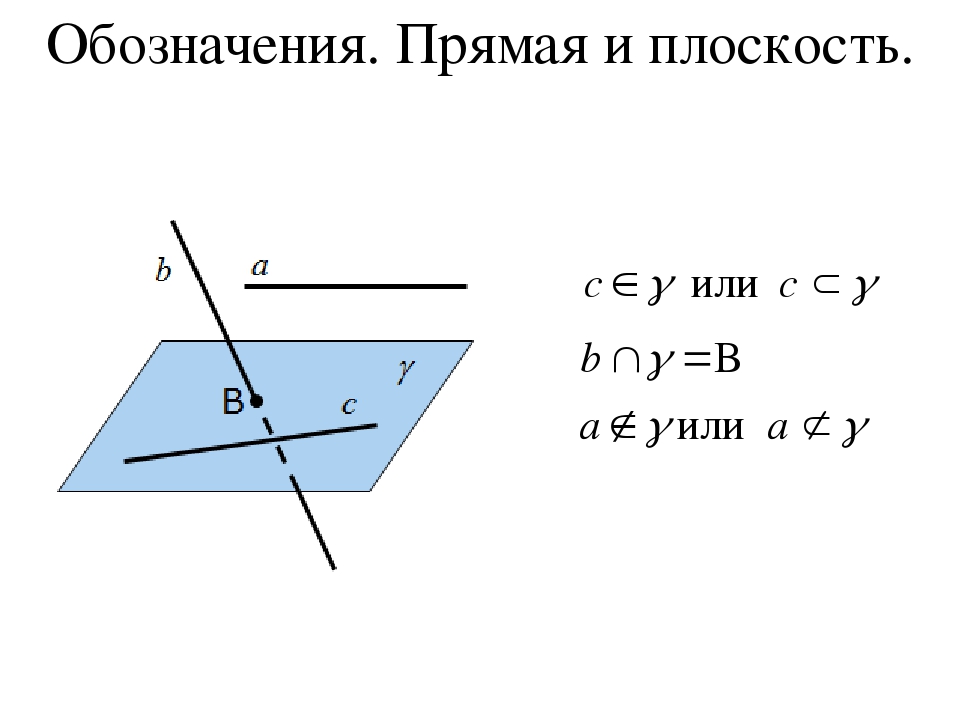
На рисунке 9.1 изображены плоскости , и .Если прямая с принадлежит плоскости , то пишут: ; если прямая не принадлежит этой плоскости, то пишут: (рис.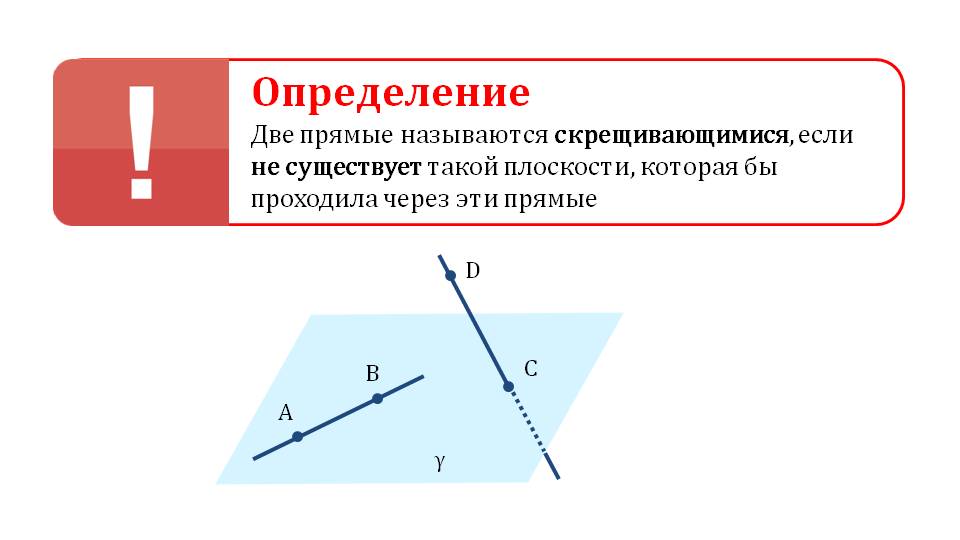 9.3).
9.3).Основные свойства взаимного расположения точек, прямых и плоскостей в пространстве выражают аксиомы стереометрии и следствия из них.
Аксиомы стереометрии
1. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
На рисунке 9.4 через точки , и проведена плоскость .2. Если две точки прямой принадлежат плоскости, то все точки этой прямой принадлежат данной плоскости.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.
Следствия из аксиом
1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. На рисунке 9.7 через прямую и точку проведена плоскость .2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну. На рисунке 9.8 через пересекающиеся прямые и проведена плоскость .Взаимное расположение прямых в пространстве
Две прямые в пространстве могут пересекаться, быть параллельными, скрещиваться или совпадать.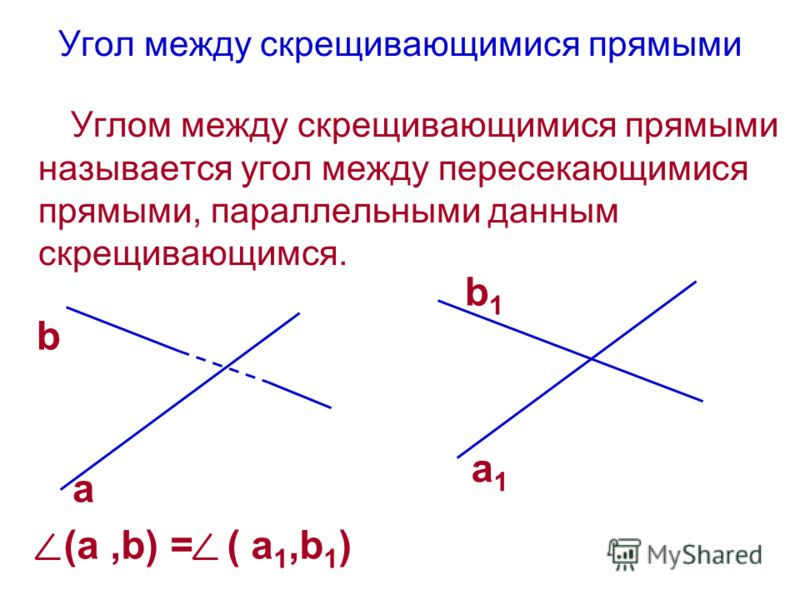
Две прямые называются перпендикулярными, если угол между ними прямой.
Две прямые в пространстве скрещиваются, если не существует плоскости, в которой они обе лежат.
Признак скрещивающихся прямых: если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.
На рисунке 9.11 изображены скрещивающиеся прямые и .Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Взаимное расположение прямых и плоскостей
В пространстве прямая может пересекать плоскость, быть ей параллельной или лежать в плоскости.
Плоскость и прямая, не принадлежащая плоскости, параллельны, если они не имеют общих точек.
Признак параллельности прямой и плоскости: если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, принадлежащей этой плоскости, то она параллельна плоскости.
Взаимное расположение плоскостей в пространстве
Две плоскости в пространстве могут совпадать, быть параллельны или пересекаться.
Две плоскости параллельны, если они не имеют общих точек.
Признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости.
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.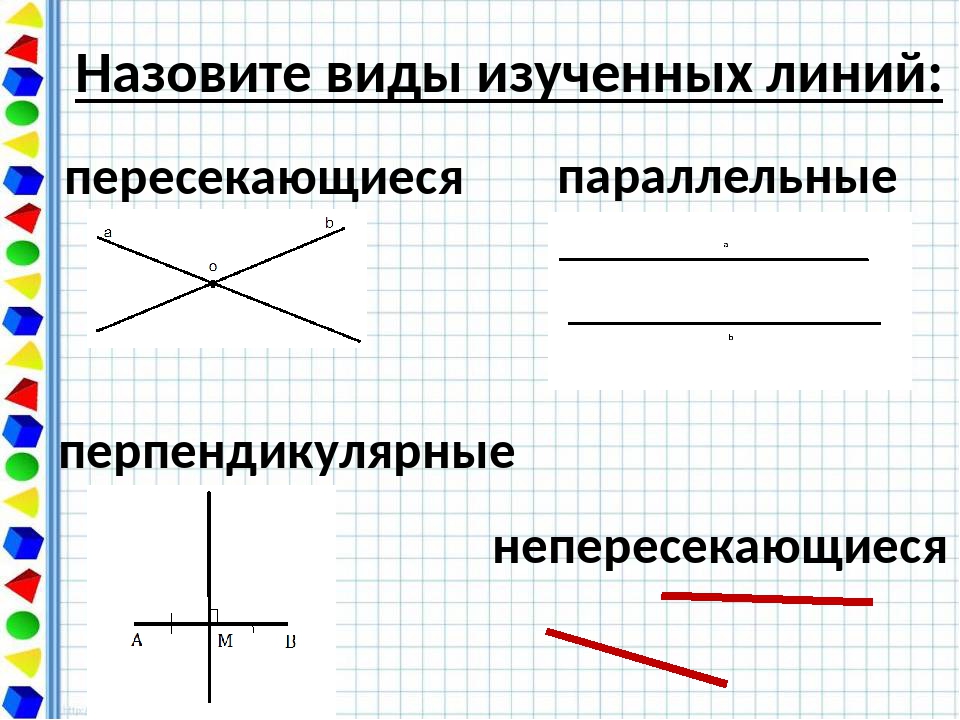
Свойства прямой, перпендикулярной плоскости
1. Два различных перпендикуляра к плоскости параллельны.
На рисунке 9.19 прямые и перпендикулярны плоскости , следовательно, .2. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к плоскости.
На рисунке 9.21 прямая – наклонная к плоскости .Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной к плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной на плоскость.
На рисунке 9.21 прямая – наклонная к плоскости, прямая – проекция этой наклонной на плоскость и . Тогда .Углом между прямой и плоскостью называют угол между прямой и ее проекцией на плоскость. На рисунке 9.22 прямая – наклонная к плоскости, прямая – проекция этой наклонной на плоскость, следовательно, угол – угол между прямой и плоскостью.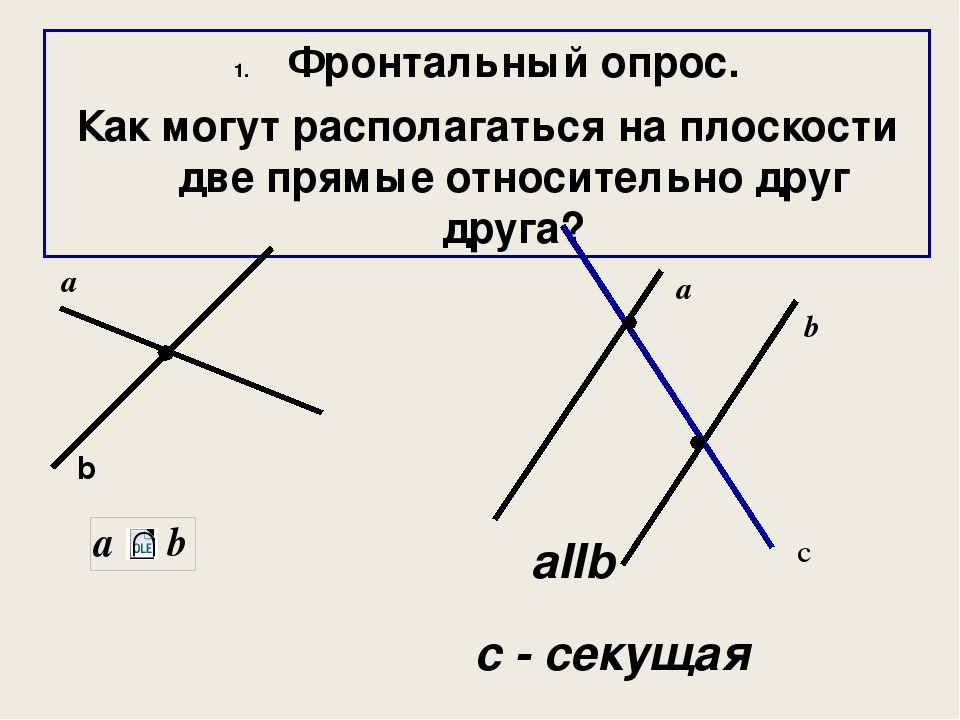
Двугранным углом называют угол, образованный двумя полуплоскостями с общей границей. Прямую, которая является общей границей этих полуплоскостей, называют ребром двугранного угла, а полуплоскости с общим ребром – гранями двугранного угла.
На рисунке 9.23 изображен двугранный угол. Полуплоскости и – грани этого угла, прямая – ребро.В результате пересечения двух плоскостей образуется четыре двугранных угла (рис. 9.24).
Двугранный угол измеряется соответствующим линейным углом. Линейным углом двугранного угла называют угол между перпендикулярами, проведенными в каждой грани к ребру.
На рисунке 9.25 угол – линейный угол двугранного угла.Двугранный угол может иметь любое значение от до . Если линейный угол двугранного угла равен , то плоскости перпендикулярны.Признак перпендикулярности плоскостей: если плоскость содержит перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.
На рисунке 9. 26 плоскости и перпендикулярны.
26 плоскости и перпендикулярны.Термины и определения начертательной геометрии
Содержание
- Термины и определения;
- Условные обозначения;
- Способы задания плоскости на чертеже.
Термины и определения
Комплексный чертеж (эпюр Монжа) – чертеж, составленный из взаимосвязанных ортогональных проекций геометрической фигуры. Чтобы преобразовать пространственный макет в эпюр, нужно совместить плоскости проекций П1 и П3 с третьей плоскостью П2, вращая П1 вокруг оси x, а П3 вокруг оси z.
Конкурирующие точки – точки, расположенные на одной проецирующей прямой, но при этом удаленные от плоскости проекций на разное расстояние.
Линии уровня – прямые, параллельные одной из плоскостей проекций.
- Горизонталь, h – прямая, параллельная горизонтальной плоскости;
- Фронталь, f – прямая, параллельная фронтальной плоскости;
- Профильная прямая, p – прямая, параллельная профильной плоскости.

Метрические задачи – это задачи, целью решения которых является нахождение натуральных величин отрезков, углов, расстояний.
Октант – часть пространства, ограниченная плоскостями проекций П1, П2, П3. В начертательной геометрии выделяют восемь октантов, нумерация и взаимное расположение которых показаны на рисунке.
Отрезок – участок прямой, ограниченный двумя точками.
Плоскости общего положения – плоскости, которые не перпендикулярны ни одной из плоскостей проекций.
Плоскости уровня – плоскости, параллельные одной из плоскостей проекций.
Позиционные задачи – это задачи, целью решения которых является определение взаимного расположения фигур, нахождение точек и линий их пересечения.
Проецирующие плоскости – плоскости, перпендикулярные одной из плоскостей проекций.
Прямые общего положения – прямые, не параллельные ни одной из плоскостей проекций.
Проецирующие прямые – прямые, перпендикулярные одной из плоскостей проекций.
Следы плоскости – прямые, по которым данная плоскость пересекается с плоскостями проекций.
Следы прямой – точки пересечения прямой с плоскостями проекций.
Угол между прямой и плоскостью – угол между прямой и её проекцией на эту плоскость.
Условные обозначения
Оси координат:
- x – ось абсцисс;
- y – ось ординат;
- z – ось аппликат.
Проекции точек:
- A’, B’, C’ … Z’ или A1, B1, C1 … Z1 – горизонтальные;
- A», B», C» … Z» или A2, B2, C2 … Z2 – фронтальные;
- A»’, B»’, C»’ … Z»’ или A3, B3, C3 … Z3 – профильные.
Проекции прямых:
- a’, b’, c’ … z’ или a1, b1, c1 … z1 – горизонтальные;
- a», b», c» … z» или a2, b2, c2 … z2 – фронтальные;
- a»’, b»’, c»’ … z»’ или a3, b3, c3 … z3 – профильные.

Плоскости проекций:
- П1 или H – горизонтальная;
- П2 или V – фронтальная;
- П3 или W – профильная.
Следы плоскости α:
- h0α – горизонтальный;
- f0α – фронтальный;
- p0α – профильный.
Следы прямой l:
- Hl – горизонтальный;
- Fl – фронтальный;
- Wl – профильный.
Способы задания плоскости на комплексном чертеже
Плоскость на комплексном чертеже может быть задана шестью различными способами:
- Тремя точками, которые не лежат на одной прямой. На рисунке это т. A, B, C.
- Прямой и точкой, не лежащей на этой прямой.
- Двумя пересекающимися прямыми.
- Двумя параллельными прямыми (пересекающимися в несобственной точке).
- Отсеком плоской фигуры Ф.
- Следами. Этот способ удобен тем, что позволяет наглядно представить расположение плоскости в пространстве.

Дополнительные материалы:
Геометрия: линии
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Слово «линии» обычно относится к «прямой линии». У него нет ширины, есть только длина. Он абсолютно прямой и может неограниченно расширяться в обоих направлениях.
У него нет ширины, есть только длина. Он абсолютно прямой и может неограниченно расширяться в обоих направлениях. Существуют разные типы линий. 1) Вертикальная 2) Горизонтальные линии
3) Пересекающиеся 4) Копланарные 5) Наклон 6) Параллельные 7) Поперечные 8) Параллельные
 Такие прямые называются пересекающимися. Точка встречи двух линий называется точкой пересечения.
Такие прямые называются пересекающимися. Точка встречи двух линий называется точкой пересечения.Здесь прямые l и m пересекаются, а O — точка пересечения.
4) Копланарность: Прямые, лежащие в одной плоскости, называются копланарными.Прямые l, m и n лежат в одной плоскости, поэтому они копланарны.
5) Наклонные линии: Две или более некомпланарных прямых, которые не пересекаются друг с другом, называются косыми линиями.Здесь прямые p и q являются наклонными, поскольку они обе лежат в двух разных плоскостях.
6) Параллельные линии: Прямые параллельны, если они всегда находятся на одинаковом расстоянии друг от друга (так называемое «равноудаленное»), и никогда не пересекаются или никогда не пересекаются.
Просто запомните:
Параллельные линии всегда находятся на одинаковом расстоянии друг от друга и никогда не касаются друг друга.Прямые «l» и «m» параллельны. Обозначается как
л || м. 7) Поперечная: Линия, разделяющая параллельные линии в двух точках, называется поперечной. Обычно обозначается буквой «т».Здесь прямые l и m — две параллельные прямые, а ‘t’ — поперечная, поскольку она пересекает две параллельные прямые в двух точках A и B.
8) Параллельные прямые: Когда две или более копланарных прямых (лежащих в одна плоскость) пересекаются друг с другом в одной точке, такие прямые называются параллельными. Точка пересечения называется точкой совпадения.
Точка пересечения называется точкой совпадения. Линии l, m и n пересекаются в точке O, поэтому точка O известна как
Базовая геометрия
• Точка
• Линии
• Углы
• Прямые-углы
• Дополнительные углы
• Дополнительные углы
• Вертикально противоположные углы
• Линейные парные углы
• Смежные углы
• Параллельные линии
• Решенные проблемы на пересекающихся линиях
• Решенные проблемы на параллельных линиях
Covid-19 повлиял на физическое взаимодействие между людьми.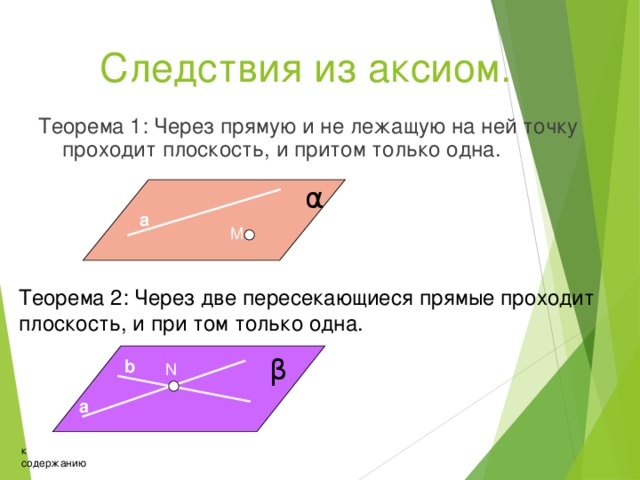
Не позволяйте этому влиять на ваше обучение.
Линии, лучи, отрезки | Параллельные линии | Перпендикулярные линии
В геометрии часто бывает ошибкой говорить, что сегмент и линия — это одно и то же.
Отрезок имеет определенное начало и определенный конец, причем каждый конец представлен точкой.
Примеры сегментов: длина стола, расстояние до прямой дороги и т. Д.
С другой стороны, линия не имеет определенного начала или конца.
Сегмент является частью линии, но линия не является частью сегмента.
Мы можем видеть так много примеров прямых линий вокруг нас, края здания, дороги, по которым мы путешествуем.
Разберемся с линиями подробнее.
Линия — это фигура, образованная, когда две точки соединены с минимальным расстоянием между ними, а оба конца продолжены до бесконечности.
Хотя линии не имеют определенного начала или конца, они представлены в нашей повседневной жизни такими примерами, как железнодорожные пути или автострады.
Луч — это часть линии, которая имеет только одну фиксированную точку, а другая точка не имеет конца.
Хотя лучи имеют фиксированное начало и не имеют определенного конца, они представлены в нашей повседневной жизни такими примерами, как солнечный свет или свет факела.
Сегмент — это часть линии, имеющая фиксированную длину, или мы можем сказать, что оба конца сегмента фиксированы. Сегменты, иногда также называемые линейными сегментами.
Хотя линейные сегменты имеют оба фиксированных конца, в нашей повседневной жизни они представлены такими примерами, как край стола, провод или столб.
Аналитический центр
- Предположим, вы привязали веревку к одной точке на Земле и начали идти, держа другой конец веревки в руке. Вы идете по прямой, спустя столько месяцев вам каким-то образом удалось вернуться в ту же точку, с которой вы начали.
 Один из ваших друзей отмечает, что когда вы двигались по веревке, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Один из ваших друзей отмечает, что когда вы двигались по веревке, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.{\ circ} \), то они перпендикулярны друг другу.
Изучите типы линий в приведенном ниже моделировании.
Горизонтальные и вертикальные линии
Линии классифицируются на основе их расположения.
Горизонтальные линииЛинии, нарисованные горизонтально, называются горизонтальными линиями.
Вертикальные линииЛинии, нарисованные вертикально, называются вертикальными линиями.
Косая или наклонная линия
Линии, которые нарисованы под наклоном или образуют угол, отличный от 0, 90, 180, 270, 360 градусов с горизонтальными или вертикальными линиями, называются наклонными или наклонными линиями.
Важные примечания
- Линия не имеет конечных точек.
- Луч имеет только одну фиксированную точку.
- Сегмент линии — это часть линии фиксированной длины.
- Перпендикулярные линии имеют угол между ними 90 градусов.
- Параллельные линии не пересекаются.
Сэм хочет узнать фигуры, состоящие только из отрезков прямых. Помогите ему выбрать правильные цифры из следующего.
Решение
Давайте обсудим каждый вариант по порядку:
Вариант А состоит из 5 линейных сегментов.
Вариант B состоит из 3 отрезков и изогнутой части.
Вариант C представляет собой круг, потому что он состоит только из изогнутых частей.
Вариант D состоит из 4 линейных сегментов.
\ (\ следовательно \) Варианты A и D верны. |
Найдите правильные типы линий на рисунке ниже.
Решение
Вариант А — пара параллельных линий
Вариант B — это пара непараллельных линий или линий пересечения.
Вариант C — это пример перпендикулярных линий.
Том выбирает точки пересечения линий, показанных на рисунке ниже, он заметил, что есть 5 точек пересечения. Он прав?
Решение
Точки пересечения любой из этих линий: \ (\ text {A, B, C, D, E, F} \)
Следовательно, всего 6 точек пересечения.
| \ (\ следовательно \) Том не прав |
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.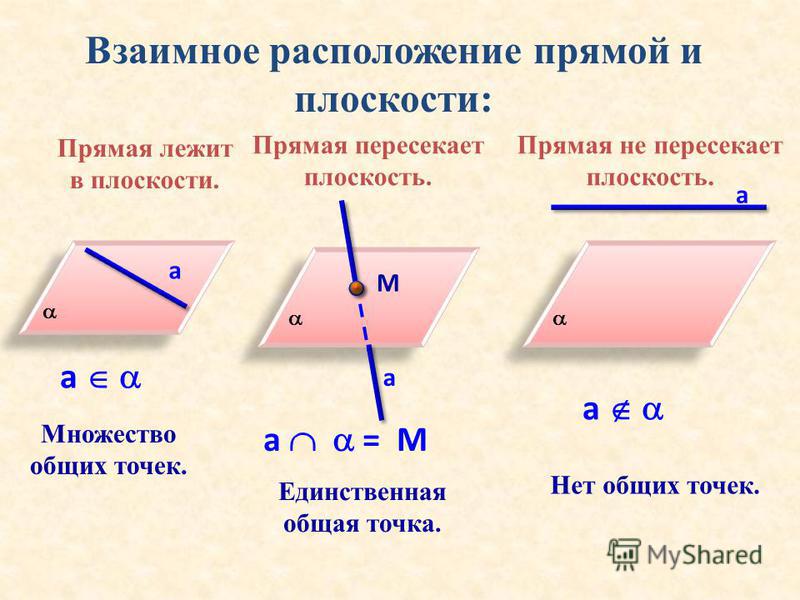
Подведем итоги
Надеемся, вам понравилось узнать о линиях с помощью интерактивных вопросов. Теперь вы сможете легко решать проблемы в режиме онлайн.
О компании CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы по линиям
1. Что такое уравнение прямой?
Общее уравнение прямой может быть записано как \ (ax + by + c = 0 \).
Где \ (a, b, c \) — константы, а \ (x, y \) — переменные.
2. Какой угол между двумя перпендикулярными линиями?
Угол между двумя перпендикулярными линиями составляет 90 градусов.
3. Что такое секущая?
Секущая линия — это линия, пересекающаяся в двух точках с окружностью.
Прямая AB — секущая к окружности.
4. Что такое касательная?
Касательная линия — это линия, которая касается окружности в одной точке.
Прямая \ (L \) касается окружности в точке \ (P \).
5. Какие параллельные прямые?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
Геометрия— для четырех непараллельных, непересекающихся линий в трехмерном пространстве две другие линии пересекаются со всеми четырьмя линиями одновременно. Как их находят?
Вот объяснение, почему в общем случае должно быть два решения.
Сначала рассмотрим задачу только для трех строк.
Если вы возьмете три линии, направления которых не копланарны, которые еще не пересекаются друг с другом и не имеют параллельных пар, то вы можете переместить и изменить масштаб оси $ x, y, z $ так, чтобы уравнения линий задаются выражениями $ L_1: (x = 0, y = 1), L_2: (y = 0, z = 1), L_3: (x = 1, z = 0) $.
Три точки $ (x_i, y_i, z_i) $ коллинеарны тогда и только тогда, когда пространство, натянутое на три $ 4 $ -вектора $ (x_i, y_i, z_i, 1) $, имеет ранг $ \ le 2 $.
Итак, в нашем случае точка $ (0,1, z) \ in L_1 $ образует линию с точками $ (x, 0,1) \ in L_2 $ и $ (1, y, 0) \ in L_3 $ при
$ ранг \ begin {pmatrix} x & 0 & 1 & 1 \\ 1 & y & 0 & 1 \\ 0 & 1 & z & 1 \ end {pmatrix} \ le 2 $
Если посмотреть на последние три столбца, определитель должен исчезнуть, так что
$ 0 = \ det \ begin {pmatrix} 0 & 1 & 1 \\ y & 0 & 1 \\ 1 & z & 1 \ end {pmatrix} = 1 + yz-y $
Итак, $ y = 1 / (1-z) $.И по причинам симметрии у нас также есть $ z-zx-1 = 0 $, так что $ x = 1-1 / z $.
Следовательно, для одной точки $ (0,1, z) $ на $ L_1 $, если $ z \ neq 0,1 $, то через нее проходит единственная прямая, которая также пересекает $ L_2 $ и $ L_3 $ ( И вы можете снять это ограничение, если будете работать в проективном пространстве и проективных линиях).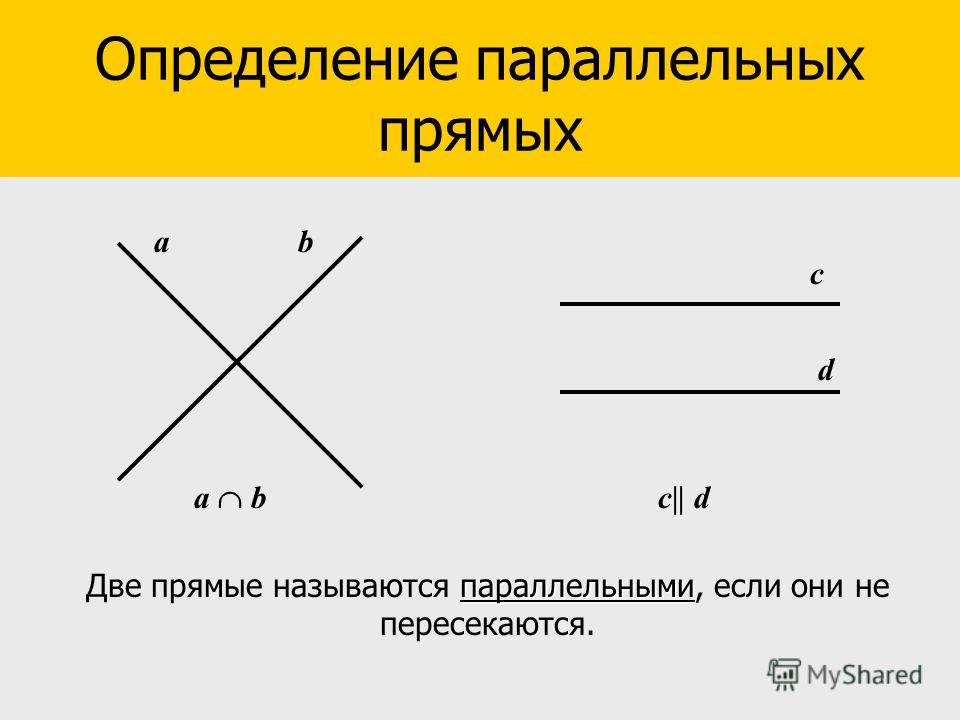 И $ y $ (и $ x $) получаются из $ z $ путем применения рациональной дроби степени $ 1 $.
И $ y $ (и $ x $) получаются из $ z $ путем применения рациональной дроби степени $ 1 $.
Если вы точка, сидящая на $ L_1 $, и вы смотрите вокруг, поворачивая голову во все стороны, вы «видите», что $ L_2 $ и $ L_3 $ «пересекаются» с вашей точки зрения только в одной точке.
Взаимодействие этого одномерного семейства прямых дает поверхность (линейчатую квадратичную поверхность), и если у вас есть четвертая линия $ L_4 $, определение двух пересекающихся линий — то же самое, что определение пересечения $ L_4 $ с поверхностью.
Для этого вам нужно уравнение поверхности. Учитывая точку $ (0,1, t) $ на $ L_1 $, вы получаете линию, проходящую через $ (0,1, t), (1- \ frac 1t, 0,1) $ и $ (1, \ гидроразрыв 1 {1-t}, 0) $. Выбор параметризации этих линий дает вам параметризацию поверхности, например
$$ s (1, \ frac 1 {1-t}, 0) + (1-s) (0,1, t) = (s , 1-s + \ frac s {1-t}, (1-s) t) $$
Затем вам нужно немного поработать, чтобы получить уравнение:
если $ (x, y, z) = (s, 1-s + \ frac s {1-t}, (1-s) t) $, то
$ s = x $
$ t = \ frac z {1-s} = \ frac z {1-x} $
, чтобы:
$ y =
1-x + \ frac x {1- \ frac z {1-x}} = 1-x + \ frac {x (1-x)} {1-xz} = \ frac {1-x-z + xz} { 1-xz} $.
Отсюда вы получаете уравнение:
$ y (1-x-z) = 1-x-z + xz $
или $ x + y + z = 1 + xy + yz + xz $.
Как и было обещано, это уравнение степени $ 2 $, поэтому оно пересекает большинство прямых в двух точках.
В качестве альтернативы, забудьте о том, как мы выбрали совершенно особую систему отсчета. При любой аффинной параметризации $ L_1 $ и $ L_2 $ (ваш $ I = I_0 + \ alpha I_1 $ для точек на $ L_1 $ и $ J = J_0 + \ beta J_1 $ для точек на $ L_2 $) будет рациональная дробь степени $ 1 $ $ f $ такая, что $ (IJ) $ пересекает $ L_3 $ тогда и только тогда, когда $ \ beta = f (\ alpha) $.Поскольку рациональная дробь полностью определяется изображением $ 3 $ точек, вы можете найти ее, посмотрев на определенные $ 3 $ прямые, пересекающие $ L_1, L_2, L_3 $, например прямую, пересекающую $ L_2 $ и $ L_3 $, которая параллельна в $ L_1 $ (который включает $ \ alpha = \ infty $), тот, который пересекает $ L_1 $ и $ L_3 $, который параллелен $ L_2 $ (который включает $ \ beta = \ infty $), и тот, который пересекает $ L_1 $ и $ L_2 $ и параллельно $ L_3 $
И если у вас есть четвертая линия $ L_4 $, тогда будет другая рациональная дробь $ 1 $ степени $ g $ такая, что $ (IJ) $ пересекает $ L_4 $ тогда и только тогда, когда $ \ beta = g (\ alpha) $.
Итак, если есть линия, которая проходит через $ I $ и пересекает $ L_2, L_3, L_4 $, тогда она должна проходить через $ J = J_0 + \ beta J_1 $ с $ \ beta = f (\ alpha) = g (\ alpha) $, и это дает уравнение на $ \ alpha $.
Если $ f (\ alpha) = (a \ alpha + b) / (c \ alpha + d) $ и $ g (\ alpha) = (a ‘\ alpha + b’) / (c ‘\ alpha + d ‘) $, установка $ f (\ alpha) = g (\ alpha) $ даст вам уравнение $ 2 $ степени $ (a \ alpha + b) (c’ \ alpha + d ‘) = (a’ \ alpha + б ‘) (с \ альфа + г) $.
Геометрия— Геометрия, образованная точкой на линии, пересекающей 3 другие линии в 3D
Общая постановка этого вопроса интересна, позвольте мне сначала разработать общую формулу для локуса.3 $ можно описать парой векторов $ (\ vec {p}, \ vec {t}) $, где $ \ vec {p} $ — точка на $ \ ell $, а $ \ vec {t} \ ne \ vec {0} $ точек по касательной:
$$ \ ell = \ {\; \ vec {p} + \ lambda \ vec {t}: t \ in \ mathbb {R} \; \} $$
Чтобы злоупотребить обозначением, для любой строки $ \ ell _? $, Помеченной индексом ‘?’, Мы будем использовать
обозначения $ \ vec {p} _? $ и $ \ vec {t} _? $ для обозначения произвольно выбранной пары векторов, описывающих эту линию. После выбора $ \ vec {p} _? $ И $ \ vec {t} _? $,
мы будем использовать $ u _? (\ vec {p}) $ как сокращение для выражения $ (\ vec {p} — \ vec {p} _?) \ times \ vec {t} _? $.
После выбора $ \ vec {p} _? $ И $ \ vec {t} _? $,
мы будем использовать $ u _? (\ vec {p}) $ как сокращение для выражения $ (\ vec {p} — \ vec {p} _?) \ times \ vec {t} _? $.
Даны любые две прямые $ \ ell_1, \ ell_2 $, не параллельные друг другу.
$ \ vec {t} _1 \ times \ vec {t} _2 $ будет отличным от нуля и перпендикулярно как $ \ vec {t} _1 $, так и $ \ vec {t} _2 $. Если мы посмотрим на две линии с направления, перпендикулярного этому вектору, изображение двух линий станет параллельным.
Их разделение будет пропорционально $ (\ vec {p} _1 — \ vec {p} _2) \ cdot \ vec {t} _1 \ times \ vec {t} _2 $.
Следствие этого:
Две непараллельные прямые $ \ ell_1 $ и $ \ ell_2 $ пересекаются тогда и только тогда, когда $$ (\ vec {p} _1 — \ vec {p} _2) \ cdot \ vec {t} _1 \ times \ vec {t} _2 = 0 \ quad \ iff \ quad u_1 (\ vec {p} _2) \ cdot \ vec {t} _2 = 0 \ quad \ iff \ quad u_2 (\ vec {p} _1) \ cdot \ vec {t} _1 = 0.
$
Даны любые три непараллельные прямые $ \ ell_1, \ ell_2, \ ell_3 $ и точка $ \ vec {p} $ за пределами трех прямых. Если $ \ vec {p} $ лежит на локусе, то можно
найти ненулевой вектор $ \ vec {t} $ такой, что
$$ u_1 (\ vec {p}) \ cdot \ vec {t} =
u_2 (\ vec {p}) \ cdot \ vec {t} =
u_3 (\ vec {p}) \ cdot \ vec {t} = 0
\ tag {* 1}
Если $ \ vec {p} $ лежит на локусе, то можно
найти ненулевой вектор $ \ vec {t} $ такой, что
$$ u_1 (\ vec {p}) \ cdot \ vec {t} =
u_2 (\ vec {p}) \ cdot \ vec {t} =
u_3 (\ vec {p}) \ cdot \ vec {t} = 0
\ tag {* 1}
Поскольку $ \ vec {p} $ не лежит на этих трех строках, три вектора $ u_i (\ vec {p}) $ равны ненулевой. Мы можем найти ненулевое значение $ \ vec {t} $, чтобы удовлетворить $ (* 1) $ тогда и только тогда, когда эти 3 вектора линейно зависят друг от друга, что эквивалентно исчезновение их тройного произведения.Подводя итог,
Условие того, что точка $ \ vec {p} $ лежит в геометрическом месте для трех непараллельных $ \ ell_1, \ ell_2, \ ell_3 $ — это $$ u_1 (\ vec {p}) \ cdot (u_2 (\ vec {p}) \ times u_3 (\ vec {p})) = 0 $$
Вернемся к нашей исходной проблеме. Пусть $ (x, y, z) $ — координаты общей точки $ \ vec {p} $. Легко видеть, что мы можем представить эти три строки как
.$$ \ begin {case} (\ vec {p} _1, \ vec {t} _1) & = ((0,2, -3), (1, 0, 0)) \\ (\ vec {p} _2, \ vec {t} _2) & = ((-1,0,3), (0, 1, 0)) \\ (\ vec {p} _3, \ vec {t} _3) & = ((1, -2,0), (0, 0, 1)) \ end {case} \ подразумевает \ begin {case} u_1 (\ vec {p}) = (0, z + 3, 2-y) \\ u_2 (\ vec {p}) = (3-z, 0, x + 1) \\ u_3 (\ vec {p}) = (y + 2,1-x, 0) \ end {case} $$ Уравнение геометрического места становится
$$ u_1 (\ vec {p})
\ cdot (u_2 (\ vec {p})
\ раз u_3 (\ vec {p})) =
\ left | \ begin {matrix}
0 & z + 3 & 2-y \\
3-z & 0 & x + 1 \\
у + 2 и 1-х и 0
\ end {matrix} \ right |
= 6xy + 2yz + 4xz + 12 = 0
$$
Итак, ответ — $ (b) $.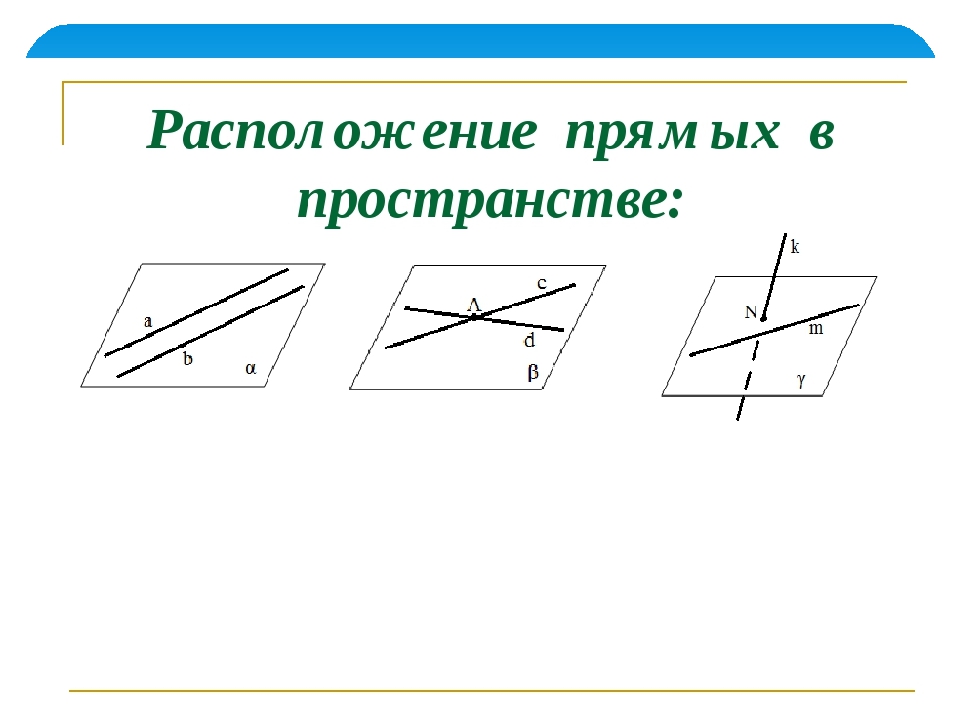
пересекающихся линий и углов — PSAT Math
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Основные геометрические термины | Ресурсы Wyzant
Ниже приведены некоторые из ключевых понятий и терминов, которые вам нужно знать, чтобы начать
ваше изучение геометрии.
Очки
В геометрии мы используем точки, чтобы указать точное местоположение. Их обычно обозначают цифрой или буквой. Поскольку точки указывают одно точное местоположение, они нульмерный. Другими словами, точки не имеют длины, ширины или высоты. Это может полезно думать о точке как о крошечной «точке» на листе бумаги.
Точки A, B и C
Строки
Линии в геометрии можно рассматривать как «прямую» линию, которую можно нарисовать на бумаге.
карандашом и линейкой.Однако вместо того, чтобы ограничить эту линию размерами
бумаги линия тянется бесконечно в обоих направлениях. Линия одномерная,
имеющий длину, но не ширину или высоту. Линии однозначно определяются двумя точками.
Таким образом, обозначим название прямой, проходящей через точки A и B как
, где двунаправленная стрелка означает, что
линия проходит через эти уникальные точки и бесконечно продолжается в обоих направлениях.
Отрезки линии
Рассмотрим задачу нарисовать «прямую» линию на листе бумаги (как мы это сделали когда думаешь о линиях). На самом деле вы создали линейный сегмент. Поскольку наш листок бумаги имеет определенные размеры, и мы не можем провести линию бесконечно в любом направлении мы построили отрезок, который где-то начинается и где-то заканчивается.Пишем имя отрезка с концами A и B в качестве . Обратите внимание, что обозначения для линий и сегменты линии отличаются, потому что сегмент линии имеет определенную длину, тогда как линия не.
Лучи
Луч — это «прямая» линия, которая начинается в определенной точке и продолжается бесконечно.
в одном направлении. У луча есть одна конечная точка, которая отмечает позицию, откуда он
начинается. Луч, начинающийся в точке A , который проходит через точку B обозначается как
. Это обозначение показывает, что луч начинается в
точка A и бесконечно продолжается в направлении точки B .
У луча есть одна конечная точка, которая отмечает позицию, откуда он
начинается. Луч, начинающийся в точке A , который проходит через точку B обозначается как
. Это обозначение показывает, что луч начинается в
точка A и бесконечно продолжается в направлении точки B .
Конечные точки
Конечные точки отмечают начало или конец отрезка линии или луча.Сегменты линии имеют две конечные точки, давая им определенную длину, тогда как лучи имеют только одну конечную точку, поэтому длину луча невозможно измерить.
Мидпойнт
Середина отрезка линии отмечает точку, в которой отрезок делится на
два равных отрезка. Другими словами, длины сегментов от любой конечной точки
до середины равны. Например, если M — средняя точка
сегмент
, тогда
.Обратите внимание, что ни линии, ни лучи
могут иметь средние точки, потому что они бесконечно простираются по крайней мере в одном направлении. Это
было бы невозможно найти середину линии или луча, который никогда не заканчивается!
Например, если M — средняя точка
сегмент
, тогда
.Обратите внимание, что ни линии, ни лучи
могут иметь средние точки, потому что они бесконечно простираются по крайней мере в одном направлении. Это
было бы невозможно найти середину линии или луча, который никогда не заканчивается!
Перекресток
Когда у нас есть линии, сегменты или лучи, которые встречаются или пересекаются в определенной точке, мы называем это точка пересечения. Другими словами, эти цифры где-то пересекаются.
Параллельный
Две прямые, которые никогда не пересекаются, называются параллельными. В случае линии
отрезки и лучи, мы должны учитывать линии, в которых они лежат. Другими словами,
мы должны рассмотреть случай, когда отрезки или лучи на самом деле были линиями,
бесконечно расширяются в обоих направлениях. Если линии, на которых они лежат, никогда не пересекаются,
их называют параллельными.Например, заявление »
параллельно
, «математически выражается как
.
Если линии, на которых они лежат, никогда не пересекаются,
их называют параллельными.Например, заявление »
параллельно
, «математически выражается как
.
Если расширять бесконечно, строки выше никогда не встретятся.
Поперечный
Трансверсаль — это линия, пересекающая как минимум две другие линии. В линии, которые пересекает поперечный крест, могут быть или не быть параллельными.
На обоих рисунках красная линия является поперечной.
Самолеты
Плоскость можно представить как двумерную плоскую поверхность, имеющую длину и ширину,
но без высоты. Плоскость неограниченно простирается во все стороны и состоит из бесконечного
количество точек и линий.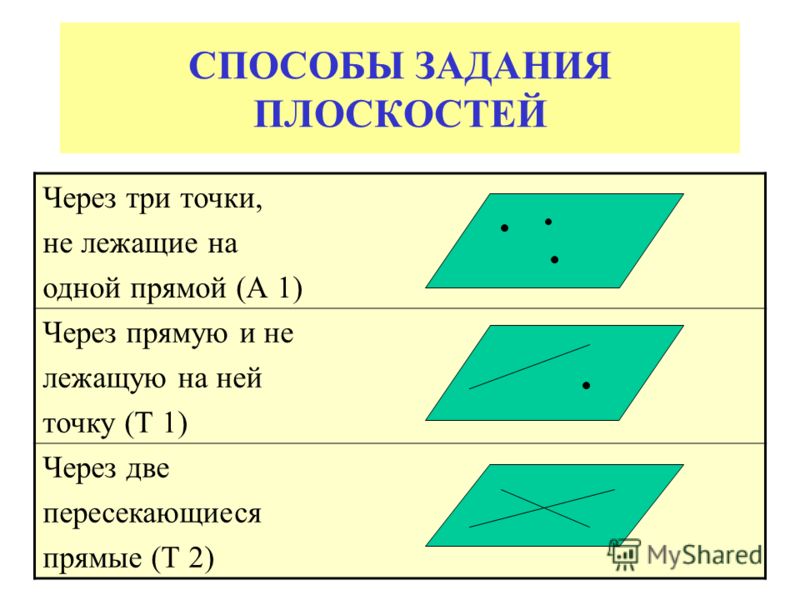 Один из способов думать о самолете — это как о листе бумаги.
с бесконечной длиной и шириной.
Один из способов думать о самолете — это как о листе бумаги.
с бесконечной длиной и шириной.
Космос
Пространство — это совокупность всех возможных точек на бесконечном количестве плоскостей. Таким образом, пространство охватывает все три измерения — длину, ширину и высоту.
Разница между параллелью и перпендикуляром
Достаточно мгновенья, чтобы понять, что повсюду линии. Когда мы ходим, разговариваем и жестикулируем, мы генерируем линии, куда бы мы ни пошли. Это увлекательно, потому что везде, куда ни глянь, есть линии.Но часто мы так заняты, настолько погружены в себя, что не замечаем их присутствия. Фактически, они уже были там. Дело не только в том, что построение линий так же повсеместно, как использование рук и ног для жестов и хождения соответственно, но, скорее, это явление, которое объединяет все аспекты нашей повседневной деятельности в единую область исследования. Линии бесконечны и, как правило, прямые.
С математической точки зрения линия определяется как бесконечный прямой путь.Это набор точек, который бесконечно простирается в двух направлениях. Они бесконечно прямые; они продолжаются и продолжаются. Линии можно использовать по-разному. Мы можем делать прямые, изогнутые и волнистые линии. Некоторые линии короткие, некоторые длинные, некоторые тонкие, а некоторые толстые. Линия показывает очертание фигуры. Один тип линии называется параллельным, значит похожим. В геометрии две прямые называются параллельными, если они равноудалены и никогда не пересекаются.Если две прямые пересекаются под прямым углом, они называются перпендикулярными.
Что такое параллель?
Когда-нибудь смотрели на железнодорожные пути? Хотя это может выглядеть так, но два стальных стержня никогда не пересекутся, потому что они параллельны. Есть много примеров параллельных линий, которые вы видите каждый день, таких как стол, стул, лестница, ящик, дверь и дорога — лишь некоторые из них. Вокруг нас есть миллионы примеров параллельных линий, которые мы видим каждый день, но не осознаем.Параллельные линии — это линии, которые никогда не пересекаются на плоскости, и они всегда находятся на одинаковом расстоянии друг от друга. Представьте себе, что было бы, если бы ступеньки лестницы не были параллельны друг другу, или, если уж на то пошло, ножки стула? Любой, кто воспользуется ступеньками или стулом, скорее всего, упадет. Две параллельные линии имеют одинаковый наклон и никогда не будут касаться друг друга. Однако, чтобы две прямые были параллельны, они должны находиться в одной плоскости.
Вокруг нас есть миллионы примеров параллельных линий, которые мы видим каждый день, но не осознаем.Параллельные линии — это линии, которые никогда не пересекаются на плоскости, и они всегда находятся на одинаковом расстоянии друг от друга. Представьте себе, что было бы, если бы ступеньки лестницы не были параллельны друг другу, или, если уж на то пошло, ножки стула? Любой, кто воспользуется ступеньками или стулом, скорее всего, упадет. Две параллельные линии имеют одинаковый наклон и никогда не будут касаться друг друга. Однако, чтобы две прямые были параллельны, они должны находиться в одной плоскости.
Что такое перпендикуляр?
Линии не всегда могут быть параллельны.Фактически, линии могут пересекаться, и когда это происходит, в точке их пересечения образуются углы. Когда две линии пересекаются под прямым углом, то есть с точностью до 90 °, линии, образующие эти углы, называются перпендикулярными. В геометрии перпендикуляр означает под прямым углом. Когда линия пересекает другую под прямым углом или 90 °, образуется перпендикулярность, означающая, что обе линии перпендикулярны друг другу.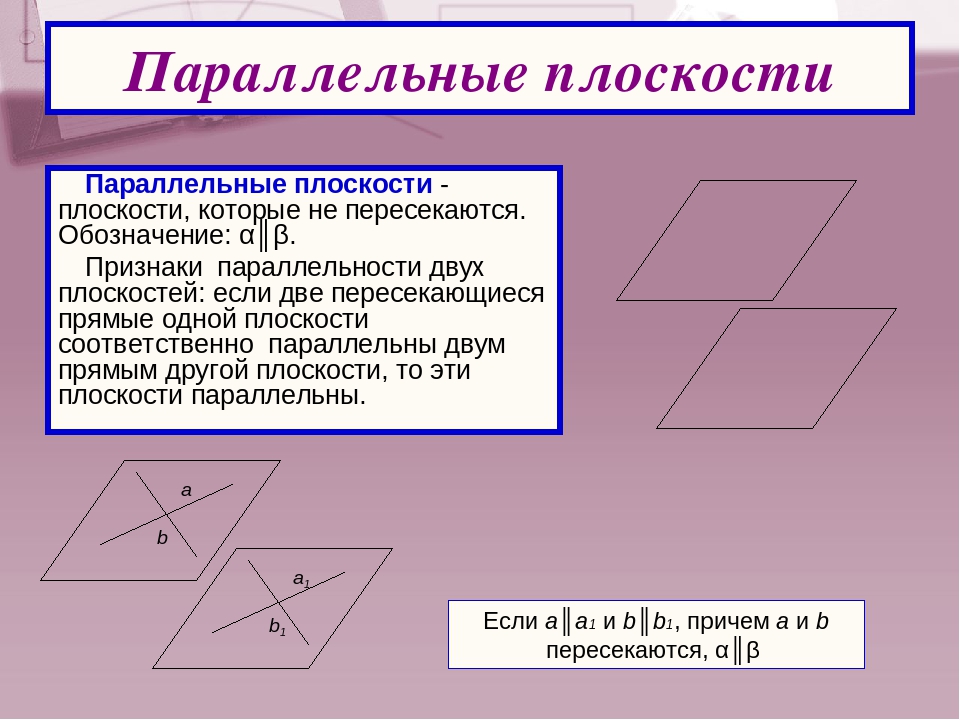 Проще говоря, линия, которая образует прямой угол с другой, называется перпендикулярной линией.Например, стены перпендикулярны полу или, когда мы стоим вертикально, мы стоим перпендикулярно плоскости. Две перпендикулярные линии образуют в точках пересечения четыре угла, все из которых равны и расположены под прямым углом.
Проще говоря, линия, которая образует прямой угол с другой, называется перпендикулярной линией.Например, стены перпендикулярны полу или, когда мы стоим вертикально, мы стоим перпендикулярно плоскости. Две перпендикулярные линии образуют в точках пересечения четыре угла, все из которых равны и расположены под прямым углом.
Разница между параллелью и перпендикуляром
Определение параллельности и перпендикуляра
Две невертикальные линии называются параллельными, если они равноудалены до конца бесконечной длины и имеют одинаковый наклон.В геометрии линии, которые одинаково удалены друг от друга во всех своих частях и никогда не пересекаются, называются параллельными линиями. Линии не всегда могут быть параллельны. Когда две пересекающиеся прямые образуют четыре угла в своих точках пересечения, все из которых равны и расположены под прямым углом, тогда говорят, что линии перпендикулярны друг другу. Две линии перпендикулярны, когда встречаются под прямым углом.
Наклон
Две линии считаются параллельными, если они равноудалены друг от друга и никогда не пересекаются и не соприкасаются.Поскольку линии одинаково удалены друг от друга, они имеют одинаковый наклон, что означает, что расстояние между линиями одинаково в разных частях. Говоря простым языком, наклон двух параллельных прямых равен. Наклон перпендикулярных линий, с другой стороны, является отрицательным, обратным друг другу, что означает, что линии пересекают друг друга под прямым углом.
Изображение параллели и перпендикуляра
Здесь две линии являются параллельными линиями и обозначены буквой «∥».
Здесь линии перпендикулярны друг другу и обозначены буквой «⊥».
Примеры параллельности и перпендикуляра
Есть множество примеров как параллельных, так и перпендикулярных линий вокруг нас, которые мы видим каждый день. Две стороны страницы, рельсы железнодорожных путей, перила лестниц, ступеньки лестницы, ножки стула, края стен и потолка, соседние телефонные столбы, каркасы зданий — все это примеры параллельных линий в реальной жизни. Некоторые реальные примеры перпендикулярных линий включают электрический столб, угол двух стен, стоящего человека, символ остановки, Стоунхендж, мосты, дерево или любую стоящую структуру, которая стоит под углом 90 градусов по отношению к поверхности или плоскости.
Некоторые реальные примеры перпендикулярных линий включают электрический столб, угол двух стен, стоящего человека, символ остановки, Стоунхендж, мосты, дерево или любую стоящую структуру, которая стоит под углом 90 градусов по отношению к поверхности или плоскости.
Параллель и перпендикуляр: сравнительная таблица
Сводка параллельных Vs. Перпендикуляр
В двух словах, слово «параллель» относится к двум равноудаленным линиям, которые никогда не пересекаются или не касаются друг друга в любой точке. Поскольку линии расположены на одинаковом расстоянии, у них одинаковый наклон, а угол между ними равен нулю. С другой стороны, когда две прямые пересекаются под прямым углом, они называются перпендикулярными. Две пересекающиеся линии образуют четыре угла в точках пересечения, все из которых равны, что означает, что углы составляют 90 градусов.Наклоны двух перпендикулярных линий противоположны друг другу.
Сагар Хиллар — плодовитый автор контента / статей / блогов, работающий старшим разработчиком / писателем контента в известной фирме по обслуживанию клиентов, базирующейся в Индии. У него есть желание исследовать самые разные темы и разрабатывать высококачественный контент, чтобы его можно было лучше всего читать. Благодаря его страсти к писательству, он имеет более 7 лет профессионального опыта в написании и редактировании услуг на самых разных печатных и электронных платформах.
У него есть желание исследовать самые разные темы и разрабатывать высококачественный контент, чтобы его можно было лучше всего читать. Благодаря его страсти к писательству, он имеет более 7 лет профессионального опыта в написании и редактировании услуг на самых разных печатных и электронных платформах.Вне своей профессиональной жизни Сагар любит общаться с людьми разных культур и происхождения. Можно сказать, что он любопытен по натуре. Он считает, что каждый — это опыт обучения, и это приносит определенное волнение, своего рода любопытство, чтобы продолжать работать. Поначалу это может показаться глупым, но через некоторое время это расслабляет и облегчает начало разговора с совершенно незнакомыми людьми — вот что он сказал ».
Последние сообщения Сагара Хиллара (посмотреть все): Если вам понравилась эта статья или наш сайт.Пожалуйста, расскажите об этом. Поделитесь им с друзьями / семьей.
Укажите
Сагар Хиллар. «Разница между параллелью и перпендикуляром».


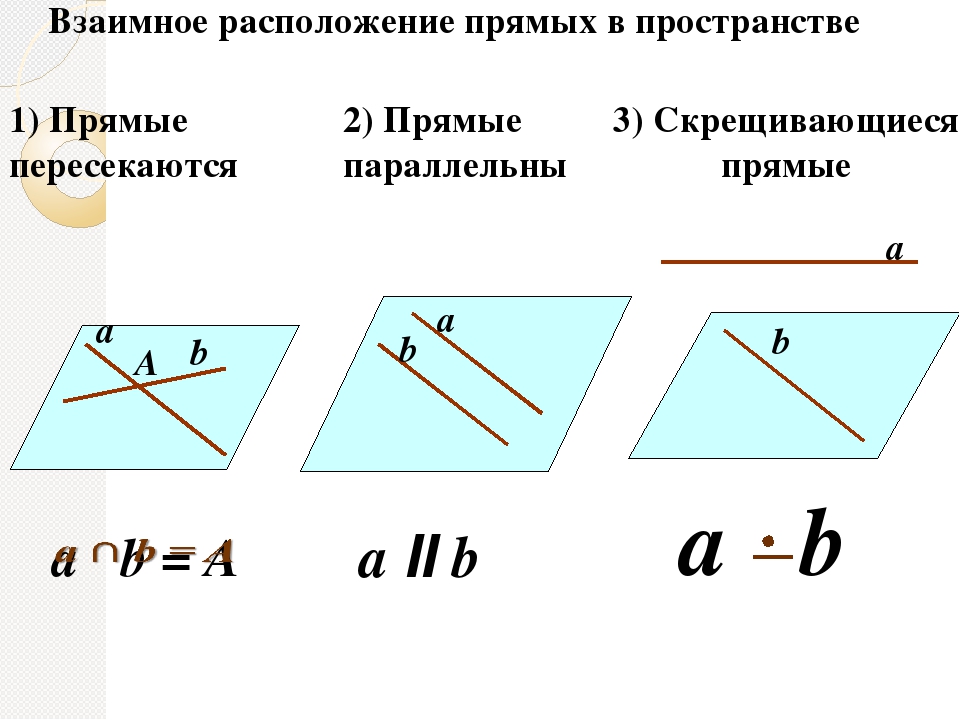 Поверхности обозначаются строчными буквами греческого алфавита:
Поверхности обозначаются строчными буквами греческого алфавита:
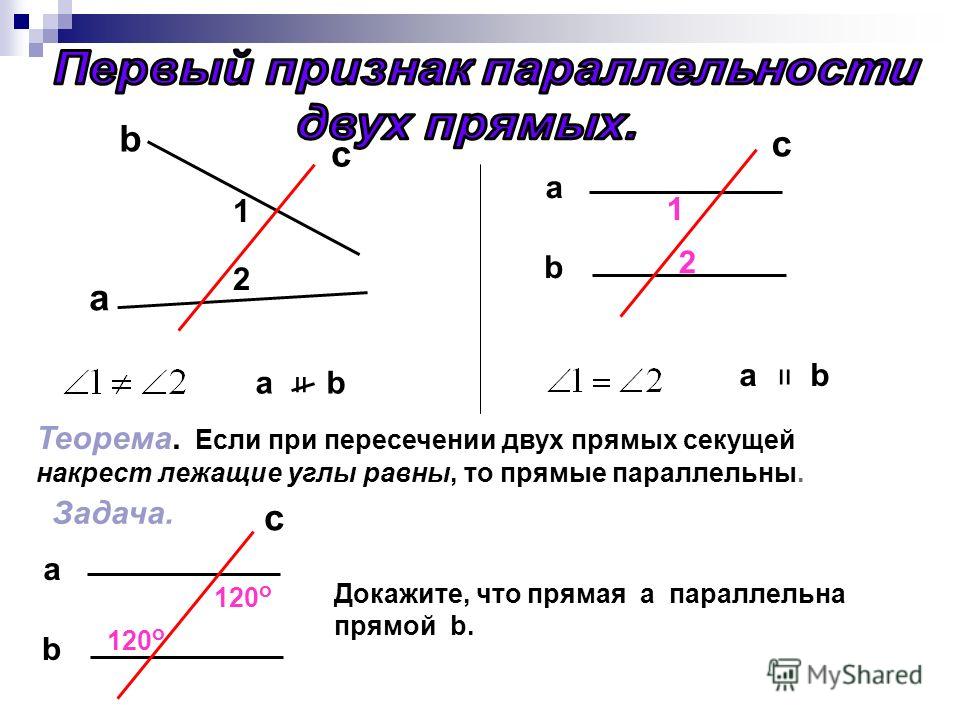
 (Прямая лежит на плоскости или плоскость проходит через прямую).
(Прямая лежит на плоскости или плоскость проходит через прямую).
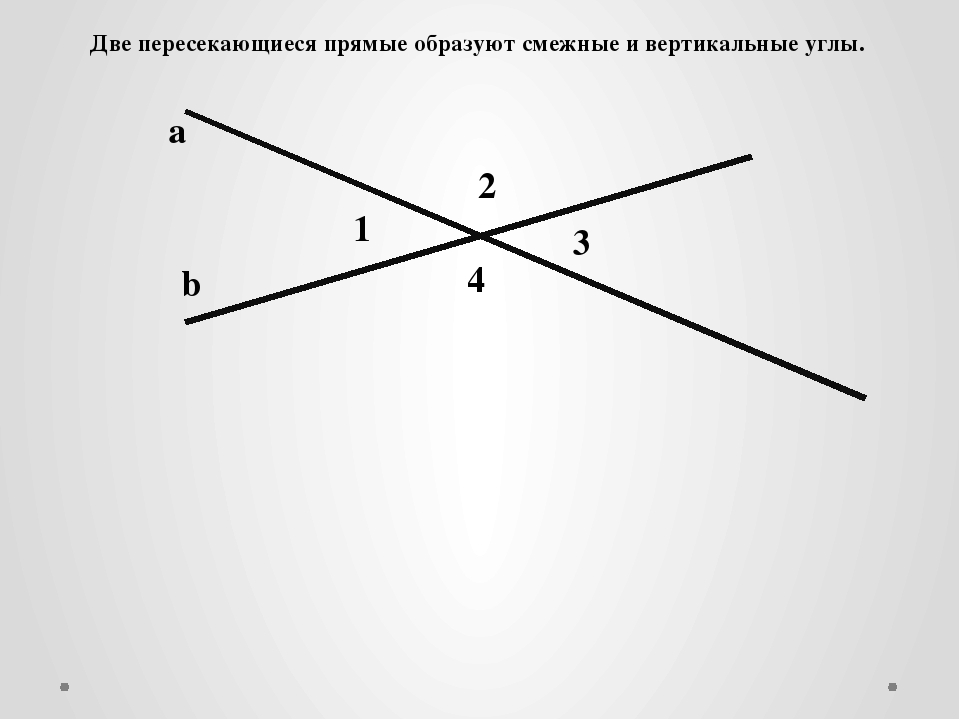


 Один из ваших друзей отмечает, что когда вы двигались по веревке, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Один из ваших друзей отмечает, что когда вы двигались по веревке, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?