Как найти сопротивление в физике: 1. Электрическое сопротивление. Закон Ома для участка электрической цепи

Содержание

Зависимость сопротивления проводника от температуры

Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.

Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр. Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.

Изменение сопротивления в зависимости от температуры

Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:

(R-R0)/R=a*t.

В данной формуле а – коэффициент пропорциональности, который называют еще температурным коэффициентом. Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.

Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.

Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.

Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.

Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.

Зависимость удельного сопротивления проводника от температуры

Попытаемся найти зависимость удельного сопротивления проводника от температуры.

Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.

Получим следующую формулу:

p=p0(1+a*t).

Температурный коэффициент можно считать постоянным, следовательно, удельное сопротивление проводника будет прямо пропорционально температуре проводника.

Данная зависимость представлена на следующем рисунке.

Попробуем разобраться, почему увеличивается сопротивление

Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.

Зависимость сопротивления проводника от температуры, широко используется в технике и физике. Например, в изготовлении термометров сопротивления.

Как найти внутреннее сопротивление формула в физике. Электродвижущая сила.

Внутреннее сопротивление источника тока

Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.

Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.

Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.

К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредственно к выходным гнездам источника подключают еще и вольтметр.

ЭДС измеряют по показанию вольтметра при разомкнутом ключе. Этот прием определения ЭДС основан на следствии из закона Ома для полной цепи, согласно которому при бесконечно большом сопротивлении внешней цепи напряжение на зажимах источника равно его ЭДС. (См. параграф «Закон Ома для полной цепи» учебника «Физика 10»).

Для определения внутреннего сопротивления источника замыкают ключ К.

При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока). Поскольку ЭДС источника равна сумме падения напряжений на внутреннем и внешнем участках цепи:

ε = U r +U R , то U r = ε -U R (1)

По закону Ома для участка цепи U r = I· r (2). Подставив равенство (2) в (1) получают:

I · r = ε — U r ,

откуда r = (ε — U R )/ J

Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо предварительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внешнем сопротивлении, а также силу тока в нем.

Ход работы

1. Подготовьте таблицу для записи результатов измерений и вычислений:

ε ,в	U r , B	i,a	r , Ом

Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.

После проверки схемы соберите электрическую цепь. Ключ разомкните.

Измерьте величину ЭДС источника.

Замкните ключ и определите показания амперметра и вольтметра.

Вычислите внутреннее сопротивление источника.

Определение эдс и внутреннего сопротивления источника тока графическим методом

Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замыкания источника тока, основанный на анализе графика зависимости напряжения на выходе источника от силы тока в цепи.

Оборудование: гальванический элемент, амперметр, вольтметр, резистор R 1 , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.

Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:

так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).

Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I К.З. — силу тока короткого замыкания (ток, который потечет в цепи источника, когда внешнее сопротивление R станет равным нулю).

ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика соответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.

Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.

Внутреннее сопротивление источника находят по тангенсу угла наклона графика относительно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомните смысл коэффициента при X).

Ход работы

Для записи результатов измерений подготовьте таблицу:

После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источнику тока, будет максимальным.

Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.

Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.

Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по вертикальной оси, а силу тока — по горизонтальной. Проведите по точкам прямую линию.

Продолжите график до пересечения с осями координат и определите величины Е и, I К.З.

Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней цепи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.

Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла наклона построенного графика к оси токов.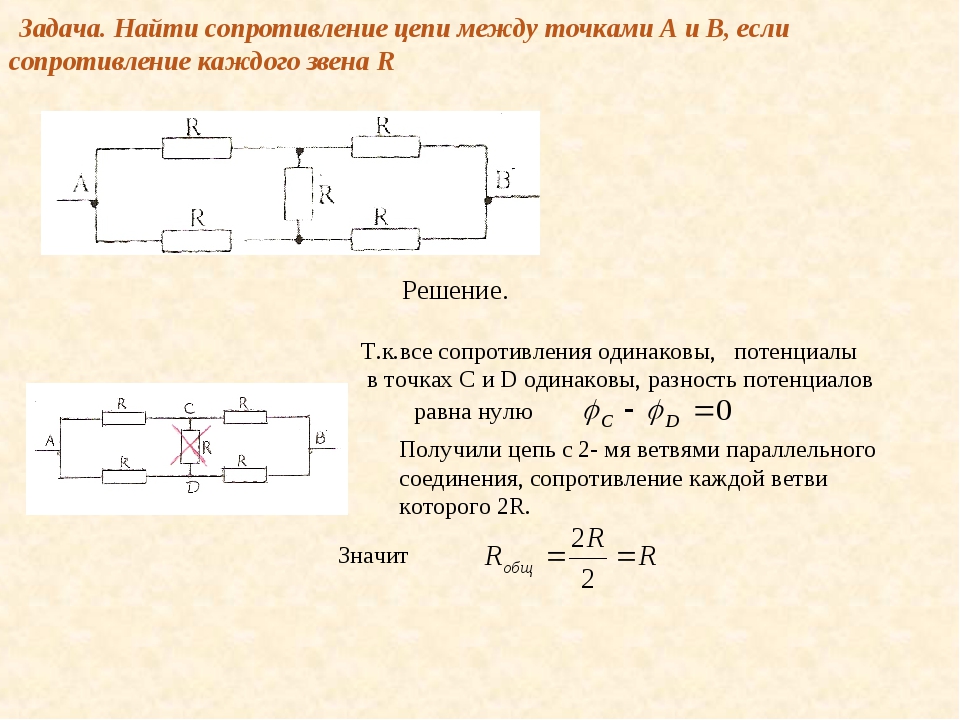

На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .

Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).

Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.

При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).

В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:

— электростатическая

— в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;

— термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;

— фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;

— химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.

Электродвижущая сила (ЭДС) — характеристика источников тока.

Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:

ɛ = A ст /q ,

где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.

Электродвижущую силу выражают в вольтах.

Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.

Внутреннее сопротивление источника тока.

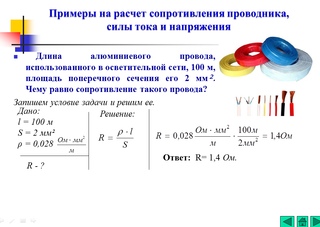
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .

В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.

Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.

ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление
Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:U — напряжение источника непосредственно на его клеммах.
Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э. д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.
Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке.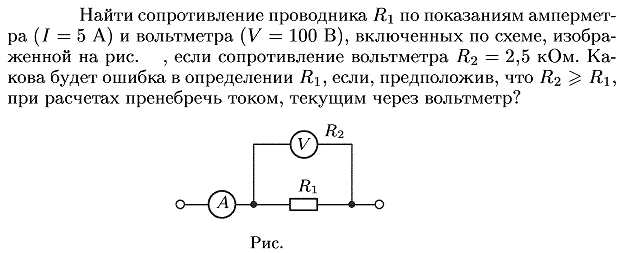 График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Попробуем решить эту задачу на конкретном примере. Электродвижущая сила источника питания составляет 4,5 В. К нему подключили нагрузку, и через неё потёк ток, равный 0,26 А. Напряжение при этом стало равным 3,7 В. Первым делом, представим себе, что внутри источника спрятана последовательная цепь из идеального источника напряжения в 4,5 В, внутреннее сопротивление которого равно нулю, а также резистора, номинал которого и требуется найти. Понятно, что на самом деле это не так, но для расчётов аналогия вполне сойдёт.

2 шаг

Запомните, что буквой U обозначают только напряжение под нагрузкой. Для обозначения же электродвижущей силы зарезервирована другая буква – E. Абсолютно точно её измерить невозможно, потому что потребуется вольтметр с бесконечным входным сопротивлением. Даже у электростатического вольтметра (электрометра) оно огромно, но не бесконечно. Но одно дело – абсолютно точно, а другое – с точностью, приемлемой на практике. Второе вполне осуществимо: нужно лишь, чтобы внутреннее сопротивление источника было пренебрежимо мало по сравнению с внутренним сопротивлением вольтметра. А пока суть да дело, посчитаем разницу между ЭДС источника и его напряжением под нагрузкой, потребляющей ток в 260 мА. E-U = 4,5-3,7 = 0,8. Это и будет падение напряжения на том “виртуальном резисторе”.

3 шаг

Ну а дальше всё просто, ибо в дело вступает классический закон Ома. Помним, что ток через нагрузку и “виртуальный резистор” одинаков, ведь они соединены последовательно. Падение напряжения на последнем (0,8 В) делим на силу тока (0,26 А) и получаем 3,08 Ома. Вот и готов ответ! Можно ещё посчитать, какая мощность рассеивается на нагрузке, а какая – бесполезно на источнике. На нагрузке рассеивается: 3,7*0,26=0,962 Вт. На источнике: 0,8*0,26=0,208 Вт. Процентное соотношение между ними вычислите самостоятельно. Но эта не единственный вид задач на нахождение внутреннего сопротивления источника. Есть и такие, в которых вместо силы тока указано сопротивление нагрузки, а остальные исходные данные такие же. Тогда надо вначале проделать ещё одно вычисление. Приведённое в условии напряжение под нагрузкой (не ЭДС!) поделить на сопротивление нагрузки. И получится сила тока в цепи. После чего, как говорят физики, “задача сведена к предыдущей”! Попробуйте составить такую задачу и решить её.

как найти длину и диаметр если дана масса и сопротивление? помогите пожалуйста)

физика и техника в 21 веке(пожалуйста жт срочно нужен что-то по типу рассказа или краткой биографии, ) пожалуйста не пиши просто так если не знаете пр … олистните

На электроплитке мощностью 1107 Вт растопили 531 г льда с начальной температурой −20 °С. Полученную воду довели до кипения, причем 40 г её обратилось … в пар. Процесс нагревания длился 44 мин. Определи КПД плитки. (Удельная теплота плавления льда λ =330000 Дж/кг, удельная теплота парообразования воды L =2260000 Дж/кг, удельная теплоёмкость льда с1 =2100 Дж/кг·°С и воды с2 =4200 Дж/кг·°С). Ответ (округли до сотых): %.

Помогите решить пожалуйста

Помогите решить задачу по физике, знаю только дано)

физика и наука в 21 веке (можете что-нибудь на эту тему написать «физика и наука в 21 веке» эт оч важно

ПОМОГИТЕ ПЖ, СРОЧНО! Визначити число атомів в V=0,12см³ золота, молярна маса якого 197 г/моль, а густина 19,3·103кг/м³

Пловець 1, що має швидкість «v», пропливає дистанцію, довжиною «L» , спочатку, в нерухомій воді озера, в обидва боки.Потім, такий самий пловець 2 / аб … о й той самий, відпочивши/, з тією ж швидкістю «v», пливе таку саму дистанцію , довжиною «L» у річці, яка тече зі швидкістю «U».Спочатку проти, а потім, за течією води. Встановіть, на яку величину відрізнятиметься час (результат) 1 пловця у річці від результату такого ж 2 пловця у нерухомій воді озера, якщо «U»< «v». Записати співвідношення * Зображення без підпису

дві мухи одночасно повзуть по стіні, висотою «L» . спочатку від підлоги до стелі , а потім, відразу ж, не зупиняючись, — до підлоги.Перша муха (муха 1 … ) повзе з постійною швидкістю «v» в обидва боки. Друга муха (муха 2) повзе вверх зі швидкістю у два рази вищою за «v», а униз — зі швидкістю у два рази меншою за «v». На яку величину відрізнятиметься результат? На скільки обжене одна муха іншу? (Який номер прийде першим?) *

Тіло рухається рівномірно по колу, радіус якого 0.5 м, маючи кінетичну енергію 10 Дж. Яка сила діє на тіло? Як вона направлена?Чому дорівнює робота ці … єї сили? *

определите кинетическую энергию 10^4 атомов гелия

Расчет сопротивления — AP Physics C Electricity

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Сопротивление и удельное сопротивление — College Physics

Зависимость сопротивления от материала и формы

Сопротивление объекта зависит от его формы и материала, из которого он сделан.Цилиндрический резистор на (рисунок) легко анализировать, и, таким образом, мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра прямо пропорционально его длине, подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше зарядов соударяется с его атомами. Чем больше диаметр цилиндра, тем больше тока он может пропускать (аналогично потоку жидкости по трубе). Фактически, обратно пропорционально площади поперечного сечения цилиндра.

Единый цилиндр длины и площади поперечного сечения. Его сопротивление потоку тока аналогично сопротивлению, которое труба оказывает потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше площадь его поперечного сечения, тем меньше сопротивление.

Для данной формы сопротивление зависит от материала, из которого изготовлен объект. Различные материалы обладают разным сопротивлением потоку заряда. Мы определяем удельное сопротивление вещества так, чтобы сопротивление объекта было прямо пропорционально.Удельное сопротивление является внутренним свойством материала, независимо от его формы или размера. Сопротивление однородного цилиндра длины и площади поперечного сечения, изготовленного из материала с удельным сопротивлением, составляет

(рисунок) дает репрезентативные значения. Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельных сопротивлений. У проводников наименьшее удельное сопротивление, а у изоляторов наибольшее; полупроводники имеют промежуточное удельное сопротивление.Проводники имеют различную, но большую плотность свободных зарядов, тогда как большинство зарядов в изоляторах связаны с атомами и не могут двигаться. Полупроводники являются промежуточными, имеют гораздо меньше свободных зарядов, чем проводники, но обладают свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников находят применение в современной электронике, о чем мы поговорим в следующих главах.

Температурное изменение сопротивления

Удельное сопротивление всех материалов зависит от температуры.Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. (Рисунок).) И наоборот, удельное сопротивление проводников увеличивается с увеличением температуры. Поскольку атомы колеблются быстрее и на больших расстояниях при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, эффективно увеличивая удельное сопротивление. При относительно небольших изменениях температуры (около или меньше) удельное сопротивление изменяется с изменением температуры, как выражается в следующем уравнении

где — исходное удельное сопротивление, а — температурный коэффициент удельного сопротивления.(См. Значения на (Рисунок) ниже.) Для более значительных изменений температуры может потребоваться нелинейное уравнение. Обратите внимание, что это положительно для металлов, то есть их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Например, у манганина (который состоит из меди, марганца и никеля) значение близко к нулю (до трех цифр на шкале (рисунок)), поэтому его удельное сопротивление незначительно меняется с температурой.Это полезно, например, для создания не зависящего от температуры эталона сопротивления.

Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает внезапный скачок, а затем увеличивается почти линейно с температурой.

Обратите внимание, что для полупроводников, перечисленных на (Рисунок), это отрицательное значение, что означает, что их удельное сопротивление уменьшается с увеличением температуры.Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшаться с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление объекта также зависит от температуры, поскольку оно прямо пропорционально. Для цилиндра, который мы знаем, и поэтому, если и не сильно изменяются с температурой, будет иметь ту же температурную зависимость, что и.(Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, и поэтому влияние температуры на и примерно на два порядка меньше, чем на.) Таким образом,

— это температурная зависимость сопротивления объекта, где — исходное сопротивление, а — сопротивление после изменения температуры. Многие термометры основаны на влиянии температуры на сопротивление. (См. (Рисунок).) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры. Устройство небольшое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Эти знакомые термометры основаны на автоматическом измерении сопротивления термистора в зависимости от температуры. (Источник: Biol, Wikimedia Commons)

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе.Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

Mr Toogood Physics — Резисторы и сопротивление

Сопротивление

В большинстве цепей ток течет из-за движения свободных электронов по проводнику. SOme-проводники имеют больше свободных электронов, чем другие, и, следовательно, являются лучшими проводниками, чем проводники с меньшим количеством свободных электронов.Материалы без свободных электронов называются изоляторами и не пропускают через них ток. Есть также материалы, которые лежат где-то посередине и будут только высвобождать электроны или пропускать ток в ответ на внешний стимул, такой как свет, тепло или электрическое поле. Эти материалы называются полупроводниками и являются строительными блоками современной цифровой технологии.

В любом металле атомы выделяют электроны, образуя кристаллическую решетку, и эти свободные электроны беспорядочно перемещаются между ионными остовами атомов металла.Обычно, поскольку движение электронов является случайным, их чистая скорость равна нулю. Однако, когда ЭДС помещается поперек проводника, электроны будут двигаться от отрицательного вывода к положительному выводу.

Рисунок 1: Если бы мы могли видеть внутри провода …

Когда электроны начинают двигаться, их случайное движение нарушается, но поскольку существует огромное количество ионных ядер, препятствующих пути между выводами, между ними происходит много столкновений. и электроны.Это приводит к тому, что траектория электронов не прямая, а общая скорость остается довольно низкой, однако теперь чистая скорость дрейфа меняется от отрицательной к положительной. Эта серия столкновений уменьшает количество энергии, которую имеют электроны, происходит передача электрической потенциальной энергии тепловой энергии. В более плохих проводниках больше столкновений и передается большее количество электрического потенциала. Это называется сопротивлением. Чем больше столкновений, тем большее количество энергии передается теплу, тем больше разность потенциалов и больше сопротивление компонента.

Резисторы — это компоненты, которые имеют фиксированное значение сопротивления в диапазоне разностей потенциалов. Ток через них прямо пропорционален разности потенциалов на них. Говорят, что они следуют закону Ома, который описан в:

$$ R = \ frac {V} {I} $$

Закон

Ома гласит, что ток через проводник прямо пропорционален разности потенциалов на нем для проводника при постоянной температуре. Проводники, такие как резисторы, ведут себя омически при фиксированных температурах, и график зависимости тока от разности потенциалов даст прямую линию, проходящую через начало координат.Сопротивление компонента обратно градиенту. Резистор с высоким сопротивлением будет иметь относительно неглубокую линию, тогда как компонент с низким сопротивлением будет иметь крутую линию. Глядя на графики ниже, мы видим, что при одинаковом увеличении p.d. синяя линия имеет меньшее увеличение тока, протекающего через нее, чем красная линия. Другие компоненты имеют отличительные формы для графиков IV , о которых вам необходимо знать.

Рисунок 2: I.V. Характеристики различных компонентов.

Лампа накаливания или старомодная лампочка работает, пропуская большой ток через тонкий кусок проволоки, который становится очень горячим и начинает раскаливаться докрасна. Это возбуждает инертный аргон внутри колбы, чтобы произвести свет. При низких значениях p.d. лампочка с проводом ведет себя омически и линия прямая, но когда п.о. увеличивается сопротивление лампы увеличивается, и линия сглаживается.

Диод является полупроводником и пропускает ток только при определенных условиях.В случае поляризованных диодов ток может течь только в одном направлении, поэтому при изменении разности потенциалов ток не может течь, что объясняет горизонтальную линию в отрицательном квадранте графика. Когда они расположены в прямом направлении, они позволяют току легко течь, но только после достижения порогового напряжения, после этого их сопротивление падает почти до нуля, и линия поднимается почти вертикально.

Наверх

Сопротивление и температура

Когда проводник нагревается, энергия передается частицам внутри проводника, и они начинают двигаться быстрее.В твердом теле, поскольку частицы находятся в фиксированном положении, это означает, что они начинают вибрировать быстрее. Это приводит к увеличению количества столкновений между частицами твердого проводника и электронами. Фактически, длина свободного пробега электронов уменьшается, и количество заряда, протекающего в секунду, также уменьшается, что приводит к увеличению сопротивления.

Нагрев может вызвать увеличение числа столкновений между электронами и частицами, и обратное также верно.Увеличение тока через проводник увеличит количество столкновений между частицами и электронами. Это вызывает передачу энергии от электронов к частицам внутри проводника и генерирует тепло. Это, в свою очередь, увеличивает сопротивление проводника. Этот эффект можно отчетливо увидеть, когда лампа накаливания включена и ток, протекающий через нее, анализируется в течение первых нескольких секунд. График ниже был получен с использованием регистратора данных в классе.

Рисунок 3: Как изменяется ток через лампочку накаливания в первые 3 секунды после ее включения.
При включении лампочки внезапно увеличивается ток, протекающий через лампочку. Поскольку колба остыла перед включением, частицы в нити накала не очень быстро вибрируют, и колба имеет низкое сопротивление. Это значит, что через него может протекать большой ток. По мере протекания тока электроны сталкиваются с ионами в нити накала и заставляют ее нагреваться, увеличивая сопротивление колбы. Это более высокое сопротивление означает, что может протекать меньший ток, и мы видим, что ток снижается до более низкого постоянного значения, известного как рабочий ток.Это хороший пример отрицательной обратной связи , где выходной сигнал системы в момент времени a приводит к тому, что выходной сигнал в момент времени b становится ниже. Это объясняет форму ВАХ лампы накаливания и то, почему сопротивление увеличивается с увеличением силы тока.
По мере увеличения тока через колбу накаливания увеличивается и температура нити накала, и, следовательно, увеличивается сопротивление. Это дает отчетливую S-образную кривую.
Связь между сопротивлением и температурой может быть использована для создания точных термометров, которые можно использовать в широком диапазоне температур.Вы проведете в классе эксперимент по созданию простейшего термометра с проводом сопротивления.
Наверх
Резисторы по цепи
Когда в цепи несколько резисторов, может потребоваться объединить их значения, чтобы вычислить общее сопротивление или ток, протекающий в цепи. Когда все резисторы включены последовательно, это довольно просто, поскольку значения резисторов можно просто сложить.В приведенном ниже примере есть три резистора, каждый с разным сопротивлением.
Рисунок 4: Добавление резисторов в последовательную цепь.
Суммарное сопротивление для этой цепи:
$$ \ large R_ {Total} = R_ {1} + R_ {2} + R_ {3} + \ cdots $$ $$ \ amount {10} {Ω} + \ amount {5} {Ω} + \ amount {12} {Ω} = \ amount {27} {Ω}; $$
Несмотря на простую взаимосвязь, выражение для полного сопротивления в последовательной цепи может быть получено, если вспомнить, что сумма разностей потенциалов на каждом резисторе равна ЭДС, подаваемой в цепь (2-й закон Кирхгофа).
\ begin {align} ε & = V_ {1} + V_ {2} + V_ {3} + \ cdots \\ \\ IR_ {T} & = IR_ {1} + IR_ {2} + IR_ {3} + \ cdots \\ \\ IR_ {T} & = I \ left (R_ {1} + R_ {2} + R_ {3} + \ cdots \ right) \\ \\ R_ {T} & = R_ {1} + R_ {2} + R_ {3} + \ cdots \ end {align}
Наверх
Резисторы параллельно
С резисторами, включенными параллельно, ситуация несколько сложнее, и стоит подумать об этом простыми словами. Разница между последовательными и параллельными цепями заключается в том, что ток разделяется на соединениях в параллельной цепи.Каждая единица заряда получает от клетки определенное количество энергии. Он будет использовать эту энергию только при прохождении через сопротивление. На диаграмме ниже каждая оранжевая точка представляет $ \ amount {1} {C} $ заряда, несущего $ \ amount {1} {J} $ электрического потенциала. На перекрестке заряды либо повернут направо, либо продолжат движение прямо. Поскольку сопротивление каждой ветви одинаково, через каждую проходит одинаковое количество тока. Каждый заряд выполняет $ \ amount {1} {J} $ работы, когда проходит через сопротивление, а это означает, что разность потенциалов на каждой ветви равна $ \ amount {1} {V} $.
Рисунок 5: Разделение тока на стыке.
Мы также можем видеть, что ток на каждой ветви меньше, чем ток до соединения, но количество энергии, которое имеет каждый кулон заряда, одинаково до и после соединения. Мы также можем применить к этой схеме два закона Кирхгофа:
Ток в каждой ветви меньше, чем ток перед соединением, но их сумма равна току перед соединением. Это удовлетворяет первому закону.
Рассматривая каждую ветвь как отдельную петлю, мы можем видеть, что разность потенциалов на каждой ветке такая же, как энергия, удерживаемая каждым кулоновским зарядом (ЭДС) перед соединением, что, согласно второму закону, должно быть равным кейс.
Мы можем применить 1-й закон Кирхгофа, чтобы вывести уравнение для полного сопротивления в параллельной цепи. Сумма токов на каждой ветви будет равна общему току на выходе из ячейки:
\ begin {align} I_ {T} & = I_ {1} + I_ {2} + I_ {3} + \ cdots \\ \\ \ frac {V} {R_ {T}} & = \ frac {V} {R_ {1}} + \ frac {V} {R_ {2}} + \ frac {V} {R_ {3}} + \ cdots \\ \\ \ frac {1} {R_ {T}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ компакт-диски \ end {align}
Это уравнение заслуживает некоторого обсуждения, поскольку оно приводит к несколько нелогичному выводу, что если мы добавим больше параллельных резисторов, общее сопротивление цепи фактически уменьшится
Если мы посмотрим на схему ниже, то увидим, что с одним резистором $ \ amount {2} {Ω} $ разность потенциалов будет $ \ amount {6} {V} $, а ток будет $ \ amount {3} {A} $.
Рис. 6: Ток, потребляемый одним резистором
Если второй резистор большего номинала добавляется параллельно первому, открывается другой путь или путь, через который протекает ток. Даже из-за того, что сопротивление на этом пути выше, через него протекает меньше тока, теперь через цепь протекает больше тока в целом. Мы можем рассчитать ток в каждой ветви, используя закон Ома, помня, что каждая ветвь будет иметь одинаковую разность потенциалов.
Рисунок 7: Ток, потребляемый двумя параллельными резисторами.
Для резистора R ₁:
\ begin {align} I & = \ frac {V} {R} \\ \\ I & = \ frac {\ amount {6.0} {V}} {\ amount {2.0} {Ω}} \\ \\ I & = \ amount {3.0} {A} \ end {align}
Для резистора R ₂:
\ begin {align} I & = \ frac {V} {R} \\ \\ I & = \ frac {\ amount {6.0} {V}} {\ amount {20} {Ω}} \\ \\ I & = \ amount {0.30} {A} \ end {align}
Суммарный ток складывается из токов на ответвлениях:
$$ I_ {Итого} = \ количество {3.0} {A} + \ amount {0.30} {A} = \ amount {3.3} {A} $$
Когда добавляется третий резистор с еще более высоким значением, чем любой из первых двух, открывается еще один путь для прохождения тока, и ток, выходящий из ячейки, снова увеличивается.
Рисунок 8: Ток, потребляемый тремя параллельными резисторами.
Поскольку каждый раз из ячейки выходит больше тока и ячейка имеет фиксированную ЭДС, следует сделать вывод, что поскольку $ R = \ frac {V} {I} $, поскольку I увеличивается каждый раз, когда добавляется резистор, то общее сопротивление цепи должно уменьшиться.
Мы можем рассчитать сопротивление конечной цепи, используя уравнение, которое мы вывели выше:
\ begin {align} \ frac {1} {R_ {T}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ \\ \ frac {1} {R_ {T}} & = \ frac {1} {\ amount {2.0} {Ω}} + \ frac {1} {\ amount {20} {Ω}} + \ frac {1} {\ amount {200} {Ω}} \\ \\ \ frac {1} {R_ {T}} & = 0,555 \ end {align}
Мы должны быть очень осторожны, так как это значение, которое мы только что вычислили, это $ \ frac {1} {R} $, а не $ R $, поэтому мы должны найти обратное этому значению, чтобы найти сопротивление.
$$ R = \ frac {1} {0.555} = \ amount {1.8} {Ω} $$
Обратите внимание, что полное сопротивление цепи на самом деле ниже, чем у наименьшего резистора в цепи. Вы можете использовать это как хороший способ проверить свои расчеты, поскольку сопротивление параллельной сети всегда будет ниже, чем сопротивление любого из резисторов в этой сети.
Комбинированные резисторы последовательно и параллельно
Когда мы сталкиваемся с более сложными схемами, которые имеют комбинации последовательно включенных резисторов и , мы должны следовать следующим правилам, чтобы найти полное сопротивление схемы и, таким образом, произвести дальнейшие вычисления:
Работайте от самой дальней от ячейки ветви и выполняйте вычисления по направлению к ячейке.
Добавьте все последовательные резисторы, которые находятся на параллельных ветвях.
Рассчитайте сопротивление параллельных сетей.
Добавьте это сопротивление к любым другим резисторам серии.
В приведенном ниже примере ветвь, содержащая R ₄ и R ₅, должна обрабатываться первой, поскольку она наиболее удалена от ячейки.
Рисунок 9: Объединение резисторов последовательно и параллельно.
$$ R_ {4} + R_ {5} = \ amount {8.0} {Ω} + \ amount {6.0} {Ω} = \ amount {14} {Ω} $$
Таким образом, эта ветвь имеет сопротивление $ \ amount {14} {Ω} $, которое можно объединить с R ₃ со значением $ \ amount {12} {Ω} $, чтобы найти полное сопротивление параллельной сети. . Мы знаем, что полное сопротивление этой части схемы будет меньше $ \ amount {12} {Ω} $, так что это позволит нам проверить наш ответ на ошибки.
\ begin {align} \ frac {1} {R_ {T}} & = \ frac {1} {R_ {3}} + \ frac {1} {R_ {4 + 5}} \\ \\ \ frac {1} {R_ {T}} & = \ frac {1} {\ amount {12} {Ω}} + \ frac {1} {\ amount {14} {Ω}} \\ \\ \ frac {1} {R_ {T}} & = 0.1547619 \\ \\ R_ {T} & = \ amount {6.5} {Ω} \ end {align}
Наконец, теперь мы можем добавить это сопротивление к двум последовательным резисторам, R ₁ и R ₂, чтобы найти общее сопротивление цепи,
.
$$ \ amount {5.0} {Ω} + \ amount {2.0} {Ω} + \ amount {6.5} {Ω} = \ amount {13.5} {Ω} $$
Теперь мы знаем полное сопротивление цепи, учитывая, что ЭДС батареи равна $ \ amount {3} {V} $, мы можем вычислить ток как $ \ amount {0.22} {A}
долл. США
Наверх
Рабочий пример
В этом примере вопрос начинается с некоторых расчетов сопротивления, прежде чем вас попросят сравнить потенциалы между отмеченными точками.
На схеме ниже показана батарея $ \ amount {12} {V} $ с незначительным внутренним сопротивлением, подключенная к комбинации из трех резисторов и термистора.
Рисунок 10: Рабочий пример 1.
Когда сопротивление термистора равно $ \ amount {5.0} {kΩ} 90 154 долл. США
рассчитать полное сопротивление цепи,
Поскольку на обеих ветвях есть по два резистора, нам нужно сложить их вместе, чтобы найти общее сопротивление на каждой ветви, прежде чем мы найдем сопротивление параллельной сети.
Сопротивление между A-E
$$ \ amount {20} {kΩ} + \ amount {20} {kΩ} = \ amount {40} {kΩ} $$
Сопротивление между B-F
$$ \ amount {10} {kΩ} + \ amount {5.0} {kΩ} = \ amount {15} {kΩ} $$
Теперь, когда мы знаем полное сопротивление каждой ветви, мы можем использовать уравнение для параллельных резисторов, чтобы найти полное сопротивление цепи.
\ begin {align} \ frac {1} {R_ {T}} & = \ frac {1} {\ amount {40} {kΩ}} + \ frac {1} {\ amount {15} {kΩ}} \\ \ frac {1} {R_ {T}} & = 0,1
6 \\ \\ R_ {T} & = \ amount {10.9} {kΩ} = \ amount {11} {kΩ} \ end {align}
При выполнении подобного вычисления с промежуточным вычислением, в данном случае для $ \ frac {1} {R_ {T}} $, вы должны либо записать полный ответ, как показано на вашем калькуляторе, либо использовать память калькулятора. настройки, чтобы сохранить их для последнего шага.Для окончательного ответа я округлил результат до того же количества значащих цифр, что и данные в вопросе.

рассчитать ток в батарее (в $ \ units {mA} $).
С сопротивлением цепи, рассчитанным в части i. и ЭДС ячейки, указанной в вопросе, мы можем использовать закон Ома, чтобы найти полный ток, протекающий в цепи:
\ begin {align} I & = \ frac {V} {R} \\ \\ I & = \ frac {\ quantity {12} {V}} {\ amount {10.9} {кОм}} \\ \\ I & = \ amount {1.10} {mA} \ end {align}
Поскольку все сопротивления выражены в $ \ units {kΩ} $, а вопрос задает ток в $ \ units {mA} $, нет необходимости преобразовывать сопротивления в $ \ units {Ω} $.

Вольтметр с высоким сопротивлением используется для измерения разности потенциалов (pd) между точками A-C, D-F и C-D по очереди.
Заполните следующую таблицу, указав показания вольтметра в каждой из трех позиций.

вольтметр положение шт. / V
A-C
D-F
C-D
Разницу потенциалов между A-C и D-F легко вычислить без дополнительных вычислений. Мы знаем, что п.д. на каждой ветви находится $ \ amount {12} {V} $, а на первой ветви два резистора имеют одинаковое значение, поэтому p.d. на каждом из них равны, в данном случае $ \ amount {6} {V} $.
Сопротивление между резистором на ответвлении в два раза больше сопротивления термистора между D-F, поэтому p.d. на резисторе будет вдвое больше p.d. поперек термистора, поэтому p.d. на термисторе находится $ \ amount {4} {V} $.
Наконец, между двумя ветвями подключается вольтметр, как показано на схеме ниже:
Рисунок 11: Рабочий пример 2.
Первоначально кажется, что решить эту проблему очень сложно, но, применив 2-й закон Кирхгофа к каждой ветви и сравнив величину электрического потенциала, удерживаемого током после прохождения через первый резистор, мы можем можно сравнить разницу потенциалов в двух ветвях.
В верхней ветви ток удерживает $ \ amount {12} {V} — \ amount {6} {V} = \ amount {6} {V} $, а в нижней ветви мы уже сделали вывод, что ток удерживается $ \ amount {4} {V} $. Разница в двух потенциалах будет показанием вольтметра и составит $ \ amount {6} {V} — \ amount {4} {V} = \ amount {2} {V} $
.
Термистор нагревается, поэтому его сопротивление уменьшается. Укажите и объясните, как это влияет на показания вольтметра в следующих положениях.

А-С
В этом вопросе мы должны дать объяснение наблюдаемого изменения на вольтметре. В этом случае показания вольтметра не изменяются. Причина в том, что сопротивление ветви цепи не изменяется, поэтому p.d. через эту ветку все то же самое.
D-F
В заключительной части вопроса отметим, что сопротивление термистора уменьшается, поэтому показания вольтметра также уменьшаются.Это потому, что p.d. прямо пропорциональна сопротивлению, поэтому большая часть п.о. через эту ветвь будет над резистором $ \ amount {10} {kΩ} $.
Наверх
Знать связь между мощностью и сопротивлением
Чтобы представить себе соотношение мощности и сопротивления, подумайте об источнике постоянного напряжения или батарее. Когда в цепи большое сопротивление, может протекать очень небольшой ток, поэтому батарея выдает очень мало энергии, и резистор не будет слишком горячим из-за меньшей мощности.{2} R \]
Где I — электрический ток, измеренный в Амперах или А.
Что такое мощность?
Мы определяем мощность как способность тела выполнять работу за единицу времени. Например, человек A выполняет 30 Дж работы за 2 часа, а другой человек B выполняет такой же объем работы за 3 часа, поэтому здесь, если мы воспользуемся следующей формулой:
Мощность = Работа / время
Случай 1: 30 / 2 = 15 Вт
Случай 2: 30/2 = 10 Вт
Мы видим, что мощность человека A больше, чем мощность человека B.Таким образом, мощность A больше, чем мощность B.
Однако с точки зрения электричества мощность определяется как произведение тока и напряжения.
P = VI
Где
В — разность потенциалов, измеряемая в вольтах.
I измеряется в амперах.
Что такое сопротивление?
При движении на высокой скорости мы должны замедлить нашу машину на некотором расстоянии до ограничителей скорости, иначе наша машина будет прыгать с большим рывком.Итак, здесь наш высокоскоростной автомобиль — это максимальный ток, протекающий по цепи (дороге), а выключатель скорости — это сопротивление, позволяющее избежать аварий или коротких замыканий в наших домах.
Итак, сопротивление — это препятствие, подключенное к цепи, чтобы избежать перелива заряда через цепь. Он измеряется в Ом, где мы обозначаем его омегой или Ом.
Формула мощности и сопротивления
Мы заметили, что приведенные выше формулы описывают соотношение между мощностью и сопротивлением.{2} R \]
Здесь мы можем видеть, что электрическая мощность прямо пропорциональна сопротивлению при поддержании постоянного I.
Отсюда мы делаем следующие выводы:
При увеличении мощности сопротивление также увеличивается, при этом ток I остается постоянным. {2}} {R} \]
Отсюда мы видим, что мощность P обратно пропорциональна сопротивлению R .
Отсюда мы можем сделать следующие выводы:
Для любой постоянной разницы потенциалов
Когда мощность в цепи высокая, сопротивление будет меньше.
Однако, если мощность низкая, сопротивление будет высоким.
Формула сопротивления мощности
Получение формулы мощности и сопротивления поможет нам понять концепцию связи мощности и сопротивления.
В физике мощность и сопротивление можно связать с помощью двух формул, которые мы подробно обсудим в этой статье.
Мы знаем, что электрическая мощность или P — это мера электрического тока I с q кулонами заряда, проходящими через разность потенциалов V (в вольтах) за время t секунд. Математически мы можем выразить это утверждение как:
P = Vq / t = VI… . {2}} {R} \]
Из приведенных выше выводов мы получили следующий вывод:
Мощность и сопротивление в электронике
В электронике мы определяем мощность как скорость выполнения работы.Итак, какие работы ведутся в области электроники? Это обычная повседневная работа или что-то еще? Опишем это простым утверждением:
Мы определяем сопротивление как сопротивление потоку электронов в цепи. Это означает, что чем больше препятствие, тем больше работы выполняется в единицу времени, чтобы заставить их течь, то есть тем больше энергии требуется, чтобы сделать их легким течением.
Из приведенного выше утверждения мы не можем отрицать тот факт, что соотношение между мощностью и сопротивлением пропорционально.
Q = It E = Расчет QV Закон Ома V = IR исследующие факторы, влияющие на сопротивление Графические характеристики ВАХ диод омический проводник лампа накаливания igcse / gcse 9-1 Physics revision notes
Электричество 3: закон Ома, экспериментальные исследования сопротивления
а также I-V графики и расчеты с использованием I = V / R, Q = It и E = QV
Редакция Доктора Брауна по физике Банкноты
Подходит для курсов GCSE / IGCSE Physics / Science или их эквивалент
Что такое закон Ома? Как вы делаете расчеты по закону Ома / с?
Какие факторы влияют на стойкость схема?
Как построить и использовать схему для исследовать закон Ома?
Как рассчитать количество электричества? заряд движется по цепи?
Субиндекс этой страницы
1.Закон Ома, простая схема исследования и расчеты V = IR
2. Движение и единица заряда, кулон, расчеты с использованием Q = It
3. Возможная разница и передача электроэнергии, E = QV расчеты
4а. Электрическое сопротивление — задействованных факторов
4б. Изучение сопротивление провода при постоянной температуре, различной длины и ширины
4с.Изучение вольт-амперные характеристики провода — пояснение графика
4д. Расследование ВАХ металлической лампы накаливания — график
4e. Изучение вольт-амперные характеристики диода — объяснение графика
См. Также ПРИЛОЖЕНИЕ 1 для обзора всей электроэнергии уравнения вам могут понадобиться
1а.Ома Закон (и упоминание других единиц, рассматриваемых в других разделах)
Закон Ома гласит, что ток через провод между двумя точками прямо пропорционален напряжению на две точки в цепи.
Он включает в себя самое фундаментальное уравнение что нужно знать для расчета электричества.
Математически это можно выразить как: я = V / R
перестановок: В = ИК а также R = V / I
I = ток в амперах, амперах, А ; мера скорости потока электрического заряда.
В = разность потенциалов, п.о., вольт, В ; мера потенциальной энергии, передаваемой электрическому заряду течет.
Разность потенциалов в цепи это энергия, передаваемая на кулон электрического заряда , что течет между двумя точками в электрической цепи.
Кулон ( C ) — это единица электрического заряда (см. Q = это уравнение примечания).
Передаваемая энергия рассчитывается от п.о. и количество электрического заряда ( Q ) перемещен p.d. в В (см. E = QV примечания к уравнениям).
R = сопротивление провода, Ом, Ом ; мера сопротивления проводника препятствовать поток заряда.
Чем больше сопротивление резистор, тем больше он сопротивляется и замедляет ток электричества.
Закон Ома означает, что R в этом уравнении является константой, не зависящей от величины протекающего электрического тока.
Закон правильно применяется к так называемому омическому сопротивлению . проводники , где протекающий ток прямо пропорционален приложенная разность потенциалов, но некоторые резисторы не подчиняются этому закону, например нагретая нить лампочка.
1b.Просто эксперимент по измерению сопротивления отдельного компонента
Если вы настроили контур 31 (правая диаграмма), вы можете измерить сопротивление постоянного резистора [R].
Изменяя напряжение источника питания с помощью переменной резистора, вы легко можете получить множество пар показаний p.d. (V) и текущий (А).
Затем используйте уравнение закона Ома (R = V / I), чтобы вычислить значение фиксированное сопротивление.
Затем вы можете усреднить значения R, рассчитанные для более надежный результат.
Более подробная информация приведена ниже, чтобы получить полную ВАХ графики, а также как получить сопротивление графическим методом.
Это основная установка для исследования вольт-амперные характеристики любого компонента Р.
1c. Примеры расчеты с использованием Ома Закон V = IR
Q1 Когда стр.d. от 4,5 В приложен к сопротивлению, течет ток 0,5 А.
Какое значение имеет резистор?
R = V / I = 4,5 / 0,5 = 9,0 Ом
Q2 Сопротивление имеет значение 50 Ом.
Какой п.о. должен быть применен к нему чтобы через него протекал ток 5,0 А?
В = ИК = 5 x 50 = 250 V
3 квартал А п.d. 240 В подается на резистор нагревательного элемента сопротивлением 30 Ом.
Сколько тока проходит через обогреватель?
I = V / R = 240/30 = 8.0 A
4 квартал Три батареи на 1,5 В были подключены последовательно к трем лампочкам.
Если амперметр измерил ток 0,50 А, какое сопротивление у каждой лампочки?
I = V / R, поэтому R = V / I = (3 x 1.5) / 0,50 = 9,0 Ом
Так как общее сопротивление = сумма сопротивления, сопротивление каждой лампочки = 9,0 / 3 = 3.0 Ом
Q5
ВЕРХ СТРАНИЦЫ и субиндекс
2. Движение заряда
2а. Расчет заряда, проходящего через точку в цепи Q = It
Ток (I в амперах) — это скорость протекания электрического заряжать вокруг цепи.
Чем больше поток заряда в данный момент времени, тем больше электрический ток.
Скорость протекания электрического заряда равна измеряется в кулонах в секунду.
Вы можете рассчитать заряд, проходящий через точку в цепи в заданное время по формуле
Q = Это
, где Q = электрический заряд в кулонах ( C ) — блок электрического заряда
I = ток в амперах ( A ) и t = время ( с )
перегруппировок из Q = It, I = Q / т и t = Q / I
Ток в 1 А равен скорость потока заряда 1 Кл / с.
2b. Примеры расчетных вопросов с участием уравнение Q = It
Q1 Если ток 3,0 А проходит через прибор в течение 1 часа 30 минут, сколько электрического заряда передается в процессе?
Q = Оно, Q = 3,0 x 1,5 x 60 x 60 = 16 200 C = 1,62 х 10 ⁴ С
Q2 Если Заряд 9000 C проходит через точку в электрической цепи в 12.0 минут, какой текущий поток?
I = Q / t = 9000 / (12 x 60) = 9000/720 = 12,5 A
Q3 Сколько времени займет электрическая цепь в минутах и секундах ток 20.0 А передать 5000 С заряда?
t = Q / I = 5000/20 = 250 секунд = 4 минут и 10 секунд
Q4 Портативный компьютер зарядное устройство пропускает ток 1.20 А на 30 минут с выходом p.d. 15.0 В.
(a) Рассчитайте, сколько заряда перенесла на компьютер аккумулятор.
Q = It = 1,2 х 30 х 60 = 2160 С
(b) Какое сопротивление зарядное устройство?
В = ИК, R = V / I = 15 / 1,2 знак равно 12,5 Ом
(c) Когда аккумулятор ноутбука полностью заряжено в нем хранит 3000 с.
Сколько времени потребуется, чтобы полностью заряжать разряженный аккумулятор?
Q = It, t = Q / I = 3000 / 1,2 = 2500 с (41 мин 40 с)
Q5
ВЕРХ СТРАНИЦЫ и субиндекс
3. Возможная разница и передача энергии
3а.Введение в электрическую энергию перевод
Передача энергии на единицу заряда = разность потенциалов (п.о.) и расчеты на основе E = QV
В предыдущем разделе мы рассмотрели, как рассчитать количество заряда, движущегося в цепи, но ничего не сказал об энергии переведен.
Напоминания :
Электрические цепи, используемые термины, условные обозначения цепей, параллельные объяснение цепей и последовательных цепей
Разница потенциалов (стр.d. в вольт, В ) — энергия, передаваемая на единицу заряда в виде электрического заряд перемещается из одной точки в другую в электрической цепи.
Измеряется вольтметром, который всегда подключается параллельно компоненту схемы.
Передача электрического тока энергия
Подумайте обо всех электрических бытовые приборы, которыми вы пользуетесь — все они нуждаются в подаче энергии для работы!
Блок питания работает на заряжается и передает ему энергию.
Работа должна производиться на зарядке для увеличения его потенциальной энергии.
Электрический заряд измеряется в кулоны (C)
Заряд и его движение уже было рассмотрено в раздел 2 (Q = It).
Заряды передают энергию компонентов по мере их прохождения, выполняя работу против сопротивления компонент.
Если работа сделана, то энергия переведен.
Если электрический заряд испытывает разность потенциалов, этот заряд будет течь, передавая энергию.
Энергия подается из энергоаккумулятора источник питания — аккумулятор, электросеть и т. Д.
При прохождении заряда по любой п.d. Падение высвобождает энергию (с более высокого уровня потенциальной энергии на более низкий).
например в тонкой проволоке сопротивление , выделяется тепло.
Разница потенциалов между двумя баллов равняется проделанной работе на единицу заряда.
разность потенциалов (В) = проделанная работа ( энергия передается в Дж) заряд (C)
т.е. 1 вольт соответствует 1 джоуля за кулон или V = J / C
Чем больше падение в p.д., тем больше энергия передается, потому что заряд начинается с большим потенциалом энергия.
Следовательно, блок питания с большим источником p.d. (В) может подавать на больше энергии в схему на единицу электрического заряда ( кулон, В).
Чем больше p.d., тем больше энергии при том же количестве электрический заряд может нести.
3b.Еще одно уравнение для расчета электрического передача энергии
В количество переносимой энергии можно рассчитать по формуле:
переданная энергия = заряд x потенциал разница.
E = QV (поэтому Q = E / V и V = E / Q )
E = передаваемая энергия в джоулях ( Дж )
Q = количество электрический заряд в кулонах ( C )
В = разность потенциалов ( В )
Отметив, что: V = E / Q = энергия, передаваемая на единицу заряда (J / C)
Попутно и несколько напоминаний:
Чем больше энергии передается в данном время, тем больше мощность устройства или электрического прибора.
П. V говорит вам, сколько энергия, передаваемая на каждую единицу электрического заряда,
так, V = E / Q , (ед. J / C), см. Расчеты E = QV ниже).
Текущий I говорит вам, сколько заряд проходит заданную точку в цепи за единицу времени (кулонов в секунду, С / с ).
Это означает, что оба p.d. В и текущий I влияет на скорость передачи энергии прибору из накопителя электроэнергии в другие накопители энергии.
И несколько математических связей на основе раздела 2. Q = It, а здесь в разделе 3 E = QV
Из Q = It и E = QV, подставляя дает E = ItV,
так (i) E = IVt (I в A, t в с, В в вольтах)
Перестановка E = IVt дает IV = Е / т
Это соединяется с уравнения для мощности
(ii) Мощность = энергия переведено / время получено = E / t (Дж / с), и
( iii ) Мощность = ток x напряжение = P (Вт) = I (A) x V (В), P = IV
Из (ii) и (iii) E / t = IV, поэтому E = IVt , что является уравнением (i) !!!
3c.Расчет q Использование на основе E = QV (иногда с участием других уравнений электричества)
Q1 Электродвигатель Модель автомобиля питается от аккумулятора 1,5 В.
Если через цепь двигателя в движущемся вагоне,
(а) сколько энергии передается?
E = QV = 120 x 1,5 = 180 Дж
(b) Опишите вероятный накопитель энергии меняется, когда машина работает.
Химическая потенциальная энергия запас батареи уменьшается и превращается в электрическую энергию.
Накопитель кинетической энергии автомобиль увеличивается из-за потери тепла от трения и звуковой энергии переданы в накопитель тепловой энергии окрестностей.
Q2 Какое количество заряд необходим для передачи 500 Дж энергии, если п.о.цепи 24,0 В?
E = QV, Q = E / V = 500/24 = 20,8 С (3 SF)
Q3 Какой потенциал разность требуется в цепи для передачи 2000 Дж энергии с заряд 50 кулонов?
E = QV, V = E / Q = 2000/50 = 40 В
4 квартал А 12.Батарея 0 В пропускает через лампу ток 2,0 А в течение 5 минут.
(a) Рассчитайте, сколько заряда прошло через лампу.
Q = It = 2 x 5 x 60 = 600 С
(b) Рассчитайте, сколько электроэнергии был перенесен лампой.
Два пути:
(i) E = QV = 600 x 12 = 7200 Дж, самый простой, но вы можете рассчитать его, не зная Q:
(ii) E = IVt = 2 x 12 x 5 x 60 = 7200 Дж
5 квартал Устройство имеет мощность 1.5 кВт и работает от сети 230 В.
Если прибор используется в течение 15 минут, сколько заряда прошло по цепи?
1,5 кВт ≡ 1500 Вт ≡ 1500 Дж / с
Общая переданная энергия = мощность x время = 1500 x 15 x 60 = 1 350 000 Дж
E = QV, поэтому Q = E / V = 1350 000/230 = 5870 С (3 SF)
Ответ можно рассчитать по другой маршрут
P = IV, I = P / V = 1500/230 = 6.522 А
Q = It = 6,522 x 15 x 60 = 5870 С (3 SF)
Q6
3d. Еще немного о разности потенциалов — действие двух последовательно соединенных резисторов
Схема 41 показывает два подключенных резистора. последовательно.
Справа показано, что происходит с p.d. по часовой стрелке по цепи (направление условного тока).
Повышается потенциальный запас аккумулятора разность зарядных потенциалов заряда до 12 В.
По мере прохождения заряда через 1-й резистор R ₁, он теряет энергию и п.д. падает на 8 В до п.п. из 4 В.
По мере прохождения заряда через 2-ю резистор R ₁, он снова теряет энергию и п.о. падает на 4 В до p.d. из 0 В.
Пока есть полная цепь, процесс повторяется.
Поскольку E = QV, выделяется вдвое больше энергии резистором R ₁ (p.d. 8 В), чем R ₂ (p.d. 4 В) для тот же ток.
ВЕРХ СТРАНИЦЫ и субиндекс
4. Электрическое сопротивление — эксперименты по исследовать ВАХ различных сопротивлений и достоверность, или в противном случае — Закона Ома
4а. Что влияет на сопротивление провода? Сопротивление постоянный?
и s — графики вольт-амперных характеристик (ВАХ) объяснил
Сопротивление цепи зависит от несколько факторов:
(i) толщина сопротивления провод — для однокомпонентного резистора
(ii) длина сопротивления провод — для однокомпонентного резистора
(iii) если более одного сопротивления, они подключены последовательно или параллельно?
(iv) температура компонента действует как сопротивление
Раздел 4.описывает и объясняет несколько примеров графиков ВАХ — которые можно исследовать с помощью схемы 31 (справа)
На принципиальной схеме 31 справа показано как можно исследовать изменение тока через сопротивление (или любой компонент) при изменении разности потенциалов.
Графики разности потенциалов тока используются, чтобы показать, как ток через компонент изменяется в зависимости от разности потенциалов на нем.
Сопротивление некоторых резисторов / компонентов действительно меняется. как действующий и п.д. изменения например диодная или лампа накаливания.
Узнайте, как и почему в разделах 4d. и 4e.
ВЕРХ СТРАНИЦЫ и субиндекс
4b. Исследование электрического сопротивления провода — изменение длины или ширины
Схема 30 показывает, как исследовать сопротивление провода
Относительно тонкая проволока закреплена на каждый конец на линейке с разметкой в миллиметрах с помощью зажимов типа «крокодил».
Вам понадобится амперметр для измерения ток в амперах и вольтметр для измерения p.d. через провод в вольт.
Провод подключается в серии с аккумуляторным блоком питания, переключателем и амперметром для измерения силы тока течет по проводу в амперах.
Вольтметр , для измерения p.d, подключен параллельно через резистивный провод.
Обратите внимание, что амперметр всегда подключается к последовательно с компонентом , но вольтметр всегда подключается параллельно по любому исследуемому компоненту.
Один конец провода, подключенный через вольтметр фиксированный (слева), но на другом конце есть зажим типа крокодил, который действует как подвижный точку контакта для размещения на различном расстоянии вдоль провода сопротивления от слева направо.
Замкните выключатель, чтобы замкнуть цепь и начинаем снимать показания.
Лучше всего открыть переключатель между показания, чтобы свести к минимуму риск нагрева провода.
Вы изменяете расстояние d (мм) от слева (0 мм) в точку дальше вправо и возьмите серию пар из п.d и текущие показания, например каждые 50 мм (можно работать в см, получается нет разницы!).
Используя закон Ома, вы вычисляете сопротивление в омах из уравнения R = V / I
Ты затем можно построить график зависимости сопротивления (Ом) от длины провода d (мм) — показано справа.
Вы должны обнаружить, что график является линейным с его начало координат x, y в точке 0,0.
Это означает, что сопротивление пропорционально длине провода .
Если не закрепить провод точно на 0 мм, график по-прежнему должен быть линейным, но начало линии не будет быть 0,0.
Если повторить эксперимент с провода разного диаметра, вы должны обнаружить, что градиент становится ниже, толще проволока.
Для провода той же длины сопротивление меньше толще проволока — хорошая аналогия — легкость, с которой вода течет через труба тонкого или большего диаметра.
ВЕРХ СТРАНИЦЫ и субиндекс
4c. Изучение ток — напряжение характеристики провода
Это эксперимент по закону Ома
Схема 31 показывает, как исследовать зависимость I от V для сопротивления
.
Главное в расследовании — найти из …
… как ток течет через резистор меняются в зависимости от разности потенциалов на нем?
Постоянный резистор представляет собой ‘компонент’ в цепи и должен иметь постоянную температуру на протяжении всего эксперимента (см. ниже температура эффекты).
В этом случае простой проволочный резистор соединены последовательно с блоком питания и амперметром.
П. измеряется по фиксированному сопротивление с вольтметром,
Тем не мение, также подключенный последовательно, добавлен переменный резистор, так что вы можете удобно изменить разность потенциалов и тем самым изменить ток протекает через компонент.
Это позволяет собрать целую серию пар показаний I и V, с помощью которых можно построить подходящие графики — в этом случай V против I, но часто делается как I против V.
Используя переменный резистор, вы постепенно увеличивайте разность потенциалов на компоненте, принимая соответствие текущему чтению, например увеличиваясь на 0,5 В. за раз. Повторите каждый читать дважды и использовать среднее значение.
После этого можно поменять местами клеммы аккумулятора. и повторить все показания.
Если вы построите p.d. по сравнению с текущим, график линейный , если он подчиняется закону Ома — тогда он называется ‘ омический проводник ‘.
Это я изобразил графиком вверху справа, а градиент равен сопротивлению в Ом .
Это соответствует закону Ома уравнение V = IR , поэтому градиент равен R.
Если график остается линейным, сопротивление остается постоянным.
Этот график не представляет показания сняты после перестановки полюсов АКБ.
Однако показывает, как получить значение сопротивления графическим методом.
Это линейный график и фраза линейный компонент может использоваться.
Для таких компонентов, как провод, который не нагревается, вы должны получить линейный график p.d. (V) против I (A) с градиент R (Ω). (правый график).
Вы должны убедиться, что провод не сильно нагревается — сразу начинает нагреваться отключите резистор («выключите») и дайте ему остыть.
Если вы построите график зависимости I от V, градиент будет 1 / R (обратная величина сопротивление), линейный график .
Этот график показывает, что вы получаете построение всех данных, включая показания I-V, снятые после реверсирования клеммы аккумулятора.
График (1) является построенный на поперечной оси. Верхняя правая половина — это ваш первый набор результатов, затем вы переверните клеммы на источнике питания и повторите эксперимент дает нижнюю левую часть графика.
Обратите внимание, что вы получите только линейный график, если температура проволоки остается постоянной .
Когда ток (А) пропорционален к p.d (V) он описывается как омический провод (подчиняется закону Ома!).
С помощью схемы 31 вы можете проверить любой резистор или любой другой тип компонента схемы, и результаты обсуждается ниже, начиная с резюме факторов, влияющих на сопротивление.
Так, сопротивление омического проводника, например цепь компонент не меняется независимо от того, проходит ли ток — постоянный градиент 1 / R для графика 1.
Это ожидаемые линейные графики для фиксированный резистор с использованием схемы 31 выше.
Думая против часовой стрелки на диаграмме, разные линии графика могут отображать убывающее сопротивление е.грамм. (i) резистивный провод становится короче при том же диаметре, или (ii) увеличение диаметра при фиксированной длине провода.
При постоянной температуре ток, протекающий через омический проводник прямо пропорционален разности потенциалов на это — уравнение: В = IR или I = V / R .
Однако это только правда, так как линейный график, если температура не изменение.
Комментарии к переменным в этом частный эксперимент с законом Ома
Ток всегда определяется сочетание п.о. (В) и сопротивление R (Ом).
Независимая переменная что мы изменяем или контролируем в эксперименте — в этом случае вы можете Считайте это р.д. управляется переменным резистором.
Одно из соглашений — построить график независимая переменная на оси x, а зависимая переменная на оси ось y.
Этот означает, что сопротивление R, является обратной величиной градиента — немного больше неудобно рассчитывать сопротивление, чем на графике зависимости V от I, где градиент — это сопротивление. Закон Ома: I = В / р.
Зависимая переменная — это то, что мы тестируем или измеряем в эксперименте, это ток I (A), который зависит от настройки переменного резистора, который, в свою очередь, контролирует разность потенциалов на резисторе.
Управляющие переменные — это то, что мы сохраняем то же самое во время эксперимента, чтобы убедиться, что это честный тест например в этом случае сохраняется температура провода и постоянная, НЕ должна изменяться — не меняйте провод и не допускайте нагреть.
ВЕРХ СТРАНИЦЫ и субиндекс
4г. Исследование вольт-амперных характеристик металла. лампа накаливания

Когда электрический заряд проходит через высокое сопротивление, подобно тонкой металлической нити накала лампы, он передает часть электроэнергия к накопителю тепловой энергии нити накала. Электрический заряд делает работают против сопротивления .
Схема 45 показывает, как можно исследовать характеристики разности токов и потенциалов нить лампочка.
Вольтметр подключен параллельно термистор, п.о. В измеряется в вольтах ( В ).
Переменный резистор позволяет варьировать п.д. и текущий поток.
Амперметр, подключенный последовательно, дает текущее значение I в амперах ( A ).
В прохождение тока нагревает нить накала и подъем в температура вызывает повышение сопротивления . Итак, нить Лампа — это неомический провод .
Этот «эффект нагрева» влияет на все резисторы.
По мере увеличения тока выделяется больше тепловой энергии, и нить накаливания становится все горячее и горячее, поэтому дальнейшее повышение температуры еще больше увеличивает сопротивление.
Это уменьшает скорость увеличения тока с Увеличение разности потенциалов .
Следовательно, градиент I-V кривая графика уменьшается, и все больше с увеличением температура — график 2. Это нелинейный график .
Если градиент меняется, тогда сопротивление меняется.
График (2) является построенный на поперечной оси.Верхняя правая половина — это ваш первый набор результатов, затем вы переверните клеммы на источнике питания и повторите эксперимент дает нижнюю левую часть графика.
Фраза нелинейная компонент может быть использован.
Когда ток (А) НЕ пропорциональная p.d (V) лампа накаливания описывается как безомический провод (не подчиняется закону Ома!).
У вас такой же график в форме треугольника. для термистор.
Теория — со ссылкой на схему металлической конструкции
Металлическая кристаллическая решетка состоит из неподвижных ионов и свободно движущихся электроны между ними. С повышением температуры ионы металла колеблются сильнее. сильно, в котором электроны сталкиваются, и это препятствует прохождению электронов, уменьшая поток плата. По мере увеличения тока вибрации увеличиваются, вызывая больше электрической энергии, которая будет преобразована в тепло — увеличивая температура И сопротивление металлической нити, тем самым еще больше понижая ток.
Итак, увеличение i n по температуре увеличивает сопротивление лампы накаливания (или большинства других резисторы) и снижает ток, протекающий для заданного p.d.
Если резистор становится слишком горячим, ток почти не будет течь.
Есть одно важное исключение к этому «правилу» см. примечания к термистор, где сопротивление фактически падает с повышение температуры.
Лампа накаливания — лишь одна из многих примеры были энергия передается с пользой , НО есть всегда теряется тепловая энергия в накопитель тепловой энергии устройства и Окрестности .
Нить накала часто изготавливается из металлический вольфрам, плавящийся при> 3400 ^o C и ярко светящийся при 2500 ^o C, но он все равно испаряется очень медленно. Инертный газ например, добавляется аргон или азот, чтобы уменьшить это испарение — любое испаренные атомы вольфрама попадают в инертный (и, следовательно, неокисляющий) Ar или N ₂ молекул и, надо надеяться, снова конденсируются на нити.
См. Сохранение энергии, передача-преобразование энергии, эффективность — расчеты
ВЕРХ СТРАНИЦЫ и субиндекс
4e. Исследование вольт-амперных характеристик диода

Модель ток через диод течет только в одном направлении — см. график 3.
Сопротивление в обратном направлении очень высока — следовательно, это фактически «односторонняя» система.
Схема 43 показывает, как можно исследовать вольт-амперная характеристика диода.
Вольтметр подключен параллельно термистор, п.о. В измеряется в вольтах ( В ).
Переменный резистор позволяет варьировать п.д. и текущий поток.
Амперметр, подключенный последовательно, дает текущее значение I в амперах ( A ).
Диод имеет очень высокое сопротивление в обратное направление .
Также есть порог р.о. (например, 1,4 В) до того, как ток вообще потечет — внимательно посмотрите на график — есть короткий горизонтальный участок, прежде чем ток поднимется с нуля и со временем становится линейным.
Таким образом, вы получаете верхнюю правую часть графика 3 по сравнению с графиками 1 и 2 выше.
Это потому, что когда вы делаете экспериментируйте, используя схему, описанную выше, по изменению подключений, вы не обнаружите никаких текущих потоков при изменении p.d.
Его нелинейный График .
Если градиент меняется, то сопротивление меняется.
Когда ток (А) НЕ пропорциональный p.d (V), диод описывается как безомический провод (не подчиняется закону Ома!).
Фраза Нелинейный компонент может быть использовано.
График (3) является построенный на поперечной оси. Верхняя правая половина — это ваш первый набор результатов, затем вы переверните клеммы на источнике питания и повторите эксперимент дает нижнюю левую часть графика.
Поскольку ток течет только в одну сторону через диод, его можно использовать для преобразования переменного тока в постоянный Текущий.
ВЕРХ СТРАНИЦЫ и субиндекс
Практическая работа по помощь в развитии ваших навыков и понимания, возможно, включала следующее:
с использованием ламп накаливания и резисторов для исследования разности потенциалов — Текущий характеристики,
ПРИЛОЖЕНИЕ 1: Важные определения, описания, формулы и ед.
Примечание: Вы можете / можете нет (но не волнуйтесь!), столкнулись со всеми этими терминами, это зависит от как далеко продвинулась ваша учеба.В вашем курсе вам может не понадобиться каждая формула — решать вам.
V разность потенциалов ( p.d ., обычно называемая « напряжение ») — это движущий потенциал, который перемещает электрический заряд вокруг цепь — обычно электронов .
Возможная разница — это работа, выполненная в перемещение единицы заряда.
Показывает, сколько энергии передается за единицу заряда, когда заряд перемещается между двумя точками в цепи е.грамм. между выводами аккумуляторной батареи.
П. в любой части цепи измеряется в вольтах, В .
Я ток — это скорость протекания электрического заряда в кулонов в секунду ( C / s ), измеряется в амперах (амперах, A ).
Количество переданного электрического заряда a give time = текущий расход в амперах x прошедшее время в секундах
Формула соединения: Q = Это , I = Q / t, t = Q / I, Q = перемещаемый электрический заряд кулонов ( C ), время т ( с )
R сопротивление в цепи, измеренное в Ом ( Ом ).
Сопротивление замедляет прохождение электрического заряда — он противостоит потоку электрического заряда .
Формула соединения: В = ИК , I = V / R, R = V / I (Это формула для Закон Ома)
P является мощность , передаваемая цепью = показатель энергии передача ( Дж / с ) и измеряется в Вт ( Вт ).
Формула соединения: P = IV , I = P / V, V = P / I также P = I ² R (см. также P = E / t ниже)
E = QV , энергия, передаваемая количеством электрического заряда потенциалом разность вольт.
переданной энергии (джоулей) = количество электрического заряда (кулоны) x разность потенциалов (вольт)
Q = E / V, V = E / Q, E = передача энергии в джоулях ( Дж ), Q = перемещенный электрический заряд ( C ), V = p.d. ( В )
E = Pt , P = E / t, t = E / P, где P = мощность ( Вт, ), E = переданная энергия ( Дж) , t = затраченное время ( с )
Передаваемая энергия в джоулях = мощность в ваттах. x время в секундах
Формула связи: Поскольку E = Pt и P = IV, передаваемая энергия E = IVt
ВЕРХ СТРАНИЦЫ и субиндекс
Что дальше?
Электричество и ревизия магнетизма индекс нот
1.Полезность электроэнергии, безопасность, передача энергии, расчеты стоимости и мощности, P = IV = I ² R, E = Pt, E = IVt
2. Электрические схемы и как их рисовать, условные обозначения схем, параллельность схемы, объяснение последовательных схем
3. Закон Ома, экспериментальные исследования сопротивление, I-V графики, расчеты V = IR, Q = It, E = QV
4. Схема устройств и как они используются? (е.грамм. термистор и LDR), соответствующие графики gcse Physical Revision
5. Подробнее о последовательных и параллельных цепях. электрические схемы, измерения и расчеты gcse физика
6. Электроснабжение «Национальной сети», экология вопросы, использование трансформаторов gcse примечания к редакции физики
7. Сравнение способов получения электроэнергии gcse Заметки о пересмотре физики (энергия 6)
8.Статическое электричество и электрические поля, использование и опасность статического электричества gcse примечания к редакции физики
9. Магнетизм — магнитные материалы — временные (индуцированные) и постоянные магниты — использует gcse физика
10. Электромагнетизм, соленоидные катушки, применение электромагнитов gcse примечания к редакции физики
11. Моторное воздействие электрического тока, электродвигатель, громкоговоритель, правило левой руки Флеминга, F = BIL
12.Эффект генератора, приложения напр. генераторы производство электричества и микрофон gcse физика
ВСЕ мои GCSE Примечания к редакции физики
ИЛИ воспользуйтесь [GOGGLE ПОИСК]
Версия IGCSE отмечает Закон Ома исследования сопротивления V = IR Q = It вычисления KS4 физика Научные заметки на Исследование сопротивления по закону Ома V = IR Q = It расчеты GCSE руководство по физике примечания к закону Ома исследования сопротивления V = IR Q = It расчеты для школ колледжей академий естествознания преподавателей изображений рисунки-диаграммы для исследования сопротивления по закону Ома V = IR Q = Он вычисляет научные исправления примечания на Исследование сопротивления по закону Ома V = IR Q = It расчеты для пересмотра модулей физики примечания по темам физики, чтобы помочь в понимании Исследование сопротивления по закону Ома V = IR Q = It расчеты университетские курсы физики карьера в науке, физике вакансии в машиностроении технический лаборант стажировка инженер стажировка по физике США 8 класс 9 класс 10 AQA Заметки о пересмотре GCSE 9-1 по физике по закону Ома исследования сопротивления V = IR Q = It вычисления GCSE примечания к закону Ома исследования сопротивления V = IR Q = It расчеты Edexcel GCSE 9-1 физика наука примечания к редакции Исследование сопротивления по закону Ома V = IR Q = It расчеты для OCR GCSE 9-1 21 век научные заметки по физике об исследованиях сопротивления по закону Ома V = IR Q = Расчет OCR GCSE 9-1 Шлюз физики примечания к пересмотру исследований сопротивления по закону Ома V = IR Q = It вычисления WJEC gcse science CCEA / CEA gcse science
ВЕРХ СТРАНИЦЫ и субиндекс

Прогнозы относительно свойств резистора: Physics Lab
Материалы
Для выполнения этой физической лаборатории вам потребуются следующие материалы:
Источник питания
Резисторы 100 Ом
1 Резистор 250 Ом
4 соединительных провода
8-проводные соединители
Цифровой мультиметр (DMM)
Бумага и карандаш
Ступени
Совет по безопасности! Убедитесь, что ваш источник питания отключен и выключен, прежде чем использовать его для построения вашей схемы.
1. Постройте эту схему:
Этот тип конфигурации резисторов называется конфигурацией серии , в которой резисторы соединены друг с другом. Как видите, электрический ток должен проходить через каждый резистор, чтобы вернуться к источнику питания.
2. Рассчитайте общее сопротивление по этой формуле для резисторов, соединенных последовательно:
Rtotal = R1 + 2 +… + n
Запишите свой расчет в тетрадь.Это то, что вы ожидаете от измеренного значения.
Совет по безопасности! Перед включением источника питания убедитесь, что вы не касаетесь каких-либо проводов в вашей цепи, и убедитесь, что ни один из ваших инструментов не касается цепи.
3. Включите источник питания. Возьмите цифровой мультиметр и измерьте расстояние от верха первого резистора R1 до низа второго резистора R2. Запишите это измерение в свой блокнот. Это полное сопротивление вашей цепи.
4. Рассчитайте общее сопротивление по этой формуле для резисторов, включенных последовательно.
Rtotal = R1 + 2 +… + n
Запишите свой расчет в тетрадь.
5. Переставьте резисторы, чтобы получилась эта цепь:
Резисторы в этой цепи имеют параллельную конфигурацию . В этом типе конфигурации ваш ток может протекать через первый или второй резистор.
6. Рассчитайте общее сопротивление, используя следующую формулу для расчета общего сопротивления резисторов, включенных параллельно:
Запишите свои расчеты в свой блокнот. Это ваше ожидаемое значение.
7. Включите источник питания. С помощью цифрового мультиметра измерьте общее сопротивление от одной общей стороны всех резисторов до другой общей стороны всех резисторов. Итак, для группы параллельных резисторов просто выберите один резистор и измерьте общее сопротивление на этом резисторе.Запишите это измерение в свой блокнот.
Поиск и устранение неисправностей
Поскольку вы работаете с цепью под напряжением, через которую проходит электричество, будьте очень осторожны, чтобы не прикасаться к ней во время эксперимента. При использовании цифрового мультиметра для измерения будьте очень осторожны, не позволяйте щупам касаться вашей цепи там, где вам не нужно проводить измерения. Это может вызвать короткое замыкание, искру или даже взрыв.
При вычислении общего сопротивления резисторов, включенных параллельно, по формуле, убедитесь, что вы взяли обратное значение после сложения дробей.
Вопросы для обсуждения
1. Что вы заметили об общем сопротивлении в последовательной конфигурации?
2. Что вы заметили об общем сопротивлении в параллельной конфигурации?
3. Соответствует ли ваше измеренное общее сопротивление расчетному общему сопротивлению?
Как это работает
Теоретически ваше измеренное общее сопротивление должно совпадать с вашим рассчитанным общим сопротивлением. Однако вы можете увидеть разницу. Это различие связано с внутренним сопротивлением ваших соединительных проводов.Обычно эта разница незначительна или очень мала. Но если ваши соединительные провода не очень хорошо проводят электричество, вы можете увидеть большую разницу. Вы можете попробовать эту лабораторную работу с разными материалами для ваших соединительных проводов, чтобы увидеть, какое влияние это может оказать на вас.
Причина, по которой последовательно соединенные резисторы складываются, заключается в том, что ваш ток должен проходить через все ваши резисторы, поэтому общее сопротивление, которое он должен пройти, складывается. Параллельно подключенные резисторы не складываются, потому что ваш электрический ток не должен проходить через все резисторы.Фактически, ваш ток может разделиться и частично пройти через каждый резистор. Поэтому общее сопротивление обычно меньше, чем у самих резисторов.
Эффективное сопротивление резисторов — Mini Physics
Во многих случаях несколько электрических устройств подключаются к одному источнику питания. Существует два основных метода соединения резисторов или других устройств между собой. Их называют последовательными и параллельными соединениями.
Вывод формулы эффективного сопротивления для последовательных и параллельных резисторов можно найти в конце этого поста.
Эффективное сопротивление резисторов
Резисторы серии
Если отдельные резисторы соединены от конца к концу, то говорят, что резисторы соединены последовательно. Эффективное сопротивление R трех резисторов сопротивлений R ₁, R ₂; и R ₃, соединенных последовательно (показано на рисунке), определяется по формуле:
$ R = R_ {1} + R_ {2} + R_ {3}
$
Как правило, если последовательно подключено n резисторов, эффективное сопротивление R определяется по формуле:
$ R = R_ {1} + R_ {2} +….+ R_ {n}
долл. США
Примечание: При последовательном соединении эффективное сопротивление R всегда больше, чем наибольшее из отдельных сопротивлений.
Сопротивление параллельно
Если каждый конец отдельных резисторов соединен друг с другом как один, то говорят, что резисторы соединены параллельно.
Эффективное сопротивление R трех резисторов сопротивлений R ₁, R ₂ и R ₃, соединенных параллельно, определяется выражением:
$ \ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}}
долл. США
Как правило, если параллельно подключено n резисторов, эффективное сопротивление R определяется по формуле:
$ \ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} +….+ \ frac {1} {R_ {n}}
долл. США
Примечание: При параллельном подключении эффективное сопротивление R всегда меньше наименьшего из отдельных сопротивлений.
Расчет эффективного сопротивления для последовательных и параллельных резисторов
Резисторы серии
Когда резисторы включены последовательно, ток через каждый резистор равен и . Обозначим ток I. Каждый резистор будет иметь свое напряжение.Если сопротивление резисторов разное ($ R_ {1} \ neq R_ {2} \ neq R_ {3} \ neq \ dots $), падение напряжения на каждом резисторе будет разным ($ V_ {1} \ neq V_ {2} \ neq V_ {3} \ neq \ dots $).
Мы знаем, что сопротивление дает $ R = \ frac {V} {I} $.
Следовательно, эффективное сопротивление всего участка резистора равно:
$$ R_ {eff} = \ frac {V_ {total}} {I} $$
Однако мы знаем, что
$$ V_ {total} = V_ {1} + V_ {2} + V_ {3} + \ dots $$
Подставляем это в уравнение эффективного сопротивления, получаем:
$$ \ begin {eqnarray} R_ {eff} & = & \ frac {V_ {total}} {I} \\ & = & \ frac {V_ {1} + V_ {2} + V_ {3} + \ точки} {I} \\ & = & \ frac {V_ {1}} {I} + \ frac {V_ {2}} {I} + \ frac {V_ {3}} {I} + \ dots \\ & = & R_ {1} + R_ {2} + R_ {3} + \ dots \ end {eqnarray} $$
Резисторы параллельные
Когда резисторы включены параллельно, падение напряжения на каждом резисторе одинаково.Обозначим напряжение как V. Каждый резистор будет иметь свое напряжение. Если сопротивление резисторов разное ($ R_ {1} \ neq R_ {2} \ neq R_ {3} \ neq \ dots $), ток через каждый резистор будет разным ($ I_ {1} \ neq I_ {2} \ neq I_ {3} \ neq \ dots $).
Мы знаем, что сопротивление дает $ R = \ frac {V} {I} $.
Следовательно, эффективное сопротивление всего участка резистора равно:
$$ R_ {eff} = \ frac {V} {I_ {total}} $$
Однако мы знаем, что
$$ I_ {total} = I_ {1} + I_ {2} + I_ {3} + \ dots $$
Подставляем это в уравнение эффективного сопротивления, получаем:
$$ \ begin {eqnarray} R_ {eff} & = & \ frac {V} {I_ {total}} \\ R_ {eff} & = & \ frac {V} {I_ {1} + I_ {2} + I_ {3} + \ dots} \\ \ frac {1} {R_ {eff}} & = & \ frac {I_ {1} + I_ {2} + I_ {3} + \ dots} {V} \ \ \ frac {1} {R_ {eff}} & = & \ frac {I_ {1}} {V} + \ frac {I_ {2}} {V} + \ frac {I_ {3}} {V} + \ dots \\ \ frac {1} {R_ {eff}} & = & \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ dots \ end {eqnarray} $$
.
No related posts.

вольтметр положение	шт. / V
A-C
D-F
C-D

Разное