Билет 12
Магнитный поток и способы его изменения. Явление электромагнитной индукции. Закон электромагнитной индукции. Величина ЭДС индукции движущегося проводника.
Магнитный поток Ф через поверхность S – скалярная физическая величина, равная произведению модуля магнитной индукции на площадь поверхности и на косинус угла между нормалью к поверхности и вектором магнитной индукции.
Ф=ВScos
Единица измерения – 1 Вб.
1 Вб – это такой магнитный поток который создаётся магнитным полем с индукцией 1 Тл через плоскую поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.
Магнитный поток характеризует число линий магнитной индукции, пронизывающих поверхность S.
Магнитный поток может изменяться при изменении: 1) магнитной индукции; 2) площади контура; 3) угла , т.е. ориентации контура в магнитном поле.
При изменении магнитного потока через замкнутый контур в этом контуре возникает индукционный ток. Протекание тока возможно в том случае, если на свободные заряды действуют сторонние силы. Следовательно, при изменении магнитного потока через поверхность, ограниченную замкнутым контуром, в этом контуре возникают сторонние силы, характеризуемые ЭДС, называемой ЭДС индукции.
Величина индукционного тока не зависит от причины изменения магнитного потока, а зависит от скорости изменения магнитного потока.
Закон Фарадея для электромагнитной индукции.
Э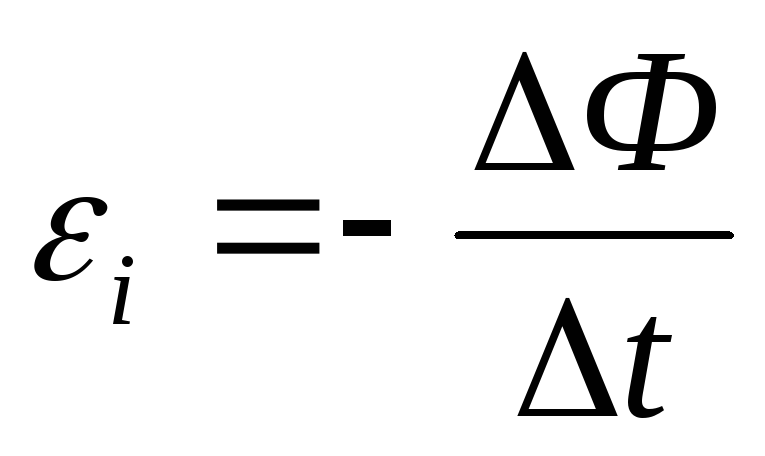 ДС
индукции в замкнутом контуре равна
скорости изменения потока магнитной
индукции через поверхность, ограниченную
контуром, взятой со знаком «-».
ДС
индукции в замкнутом контуре равна
скорости изменения потока магнитной
индукции через поверхность, ограниченную
контуром, взятой со знаком «-».
Знак минус объясняется правилом Ленца, которое определяет направление индукционного тока.
Правило Ленца.
ЭДС индукции создаёт в замкнутом контуре такой индукционный ток, который своим магнитным полем стремится компенсировать изменение потока внешнего магнитного поля.
Причина возникновения ЭДС индукции в замкнутом контуре зависит от того, каким образом изменился поток.
Возникновение ЭДС в движущемся проводнике объясняется действием на свободные заряды силы Лоренца. Величина ЭДС индукции движущегося проводника равна
i= B l v sin
где В – индукция магнитного поля, l – длина проводника, v – скорость проводника, — угол между векторами скорости и магнитной индукции.
Направление индукционного тока в контуре с перемещающимся проводником можно определить с помощью правила правой руки.
Если правую руку расположить вдоль проводника так, чтобы линии магнитной индукции входили в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике.
Возникновение ЭДС в неподвижном замкнутом проводнике, находящимся в изменяющемся магнитном поле, объясняется возникновением вихревого электрического поля.
Вихревое электрическое поле появляется при изменении магнитного поля и существует независимо от того, имеется ли в данной точке пространства замкнутый проводник или нет. Силовые линии этого поля замкнуты.
Билет 13
Потокосцепление и индуктивность. Явление самоиндукции. Величина ЭДС самоиндукции. Энергия магнитного поля.
Электрический ток, проходящий по замкнутому контуру, создаёт в окружающем пространстве магнитное поле, часть линий которого пересекает поверхность, ограниченную этим же контуром. Таким образом, получается, что контур пронизывается своим собственным потоком. Величина потока пропорциональна величине магнитной индукции, которая в свою очередь пропорциональна силе тока, протекающего по контуру. Следовательно, величина потока прямопропорциональна силе тока.
Ф Ф=LI
где коэффициент пропорциональности L – называется индуктивностью контура.
Индуктивность – скалярная физическая величина, равная собственному магнитному потоку, пронизывающему контур, при силе тока в контуре 1 А.
Е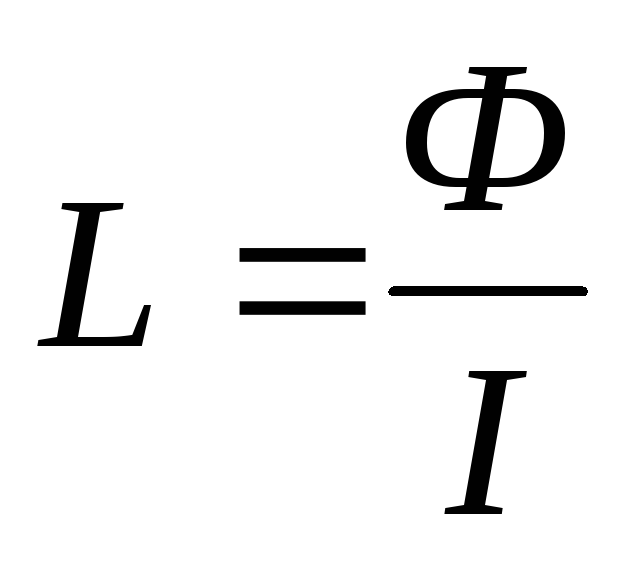 диница
измерения индуктивности1
генри.
диница
измерения индуктивности1
генри.
1 Гн – это индуктивность такого контура, в котором при силе тока 1 А возникает магнитный поток через контур, равный 1 Вб.
Магнитный поток через один виток соленоида Ф=ВS, а через N витков полный магнитный поток, который называется
=ВSN
Т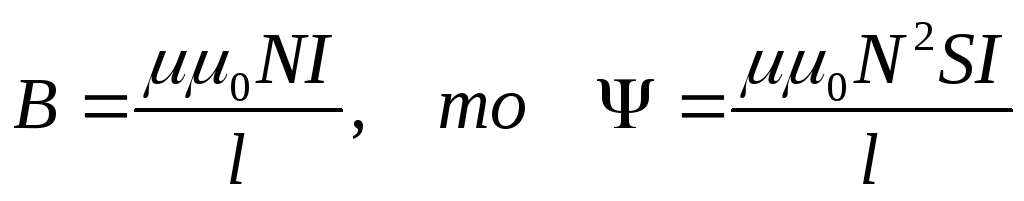 ак
как модуль магнитной индукции магнитного
поля внутри соленоида
ак
как модуль магнитной индукции магнитного
поля внутри соленоида
С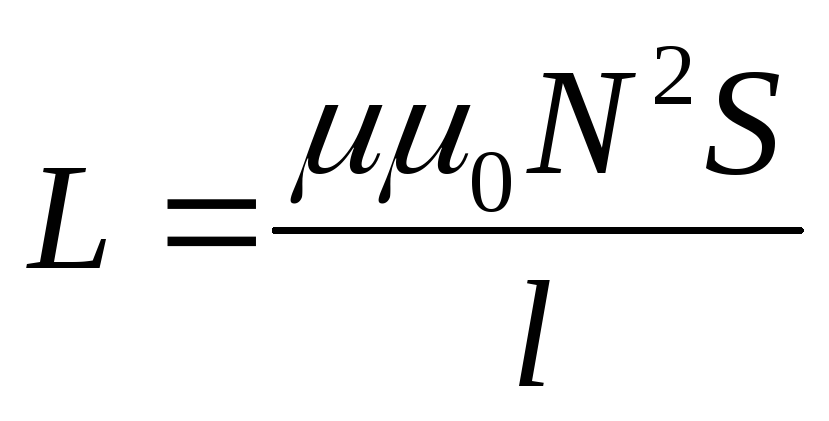 равнивая
полученное выражение для потокосцеления
иLI,
получим формулу для расчёта индуктивности
соленоида.
равнивая
полученное выражение для потокосцеления
иLI,
получим формулу для расчёта индуктивности
соленоида.
где N – количество витков соленоида, S – площадь витка, l – длина соленоида.
Если ток, протекающий в контуре, начинает изменяться, то изменяется и создаваемое им магнитное поле, а следовательно, и магнитный поток, пронизывающий контур. Согласно закону Фарадея, в контуре возникает ЭДС индукции, которая называется
З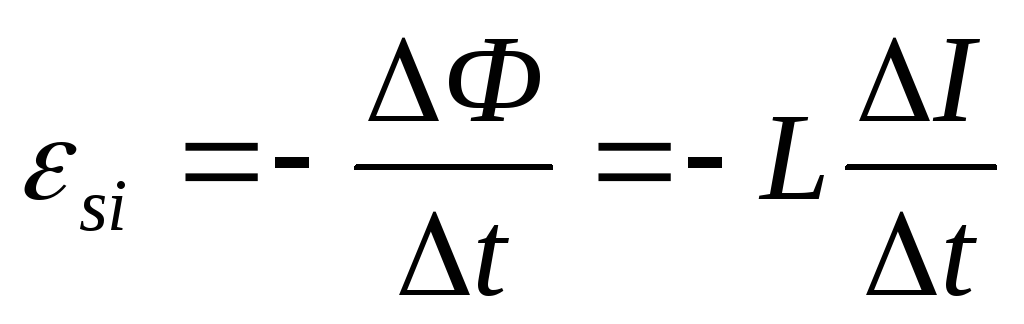 нак
«-» соответствует правилу Ленца.
нак
«-» соответствует правилу Ленца.
Отсюда следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Подключим контур к источнику тока. В контуре за счёт разности потенциалов на зажимах источника начинается перемещение зарядов. Ток в контуре возрастает. Следовательно, в контуре возникает ЭДС самоиндукции, препятствующая нарастанию тока. Работа источника тока по преодолению ЭДС самоиндукции и установлению тока идёт на создание магнитного поля.
Магнитное поле, также как электрическое, является носителем энергии. Энергия магнитного поля равна работе сторонних сил источника против ЭДС самоиндукции.
П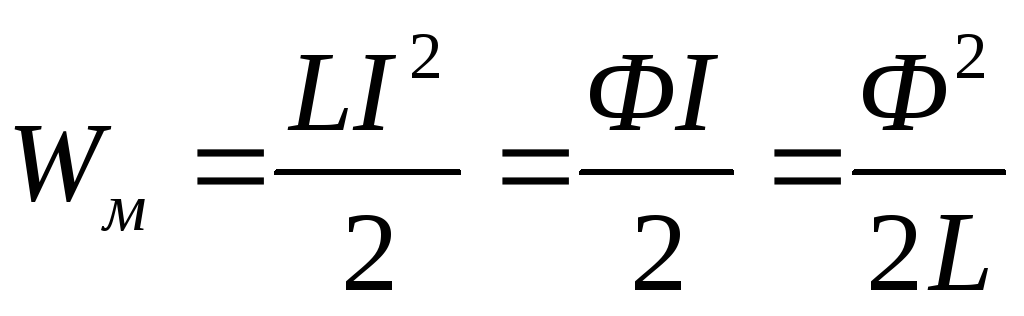 ри
отключении контура от источника тока
возникает ЭДС самоиндукции и по контуру
протекает индукционный ток. В результате
выделения теплоты Джоуля-Ленца, контур
нагревается. Следовательно, энергия
магнитного поля переходит во внутреннюю
энергию проводника.
ри
отключении контура от источника тока
возникает ЭДС самоиндукции и по контуру
протекает индукционный ток. В результате
выделения теплоты Джоуля-Ленца, контур
нагревается. Следовательно, энергия
магнитного поля переходит во внутреннюю
энергию проводника.
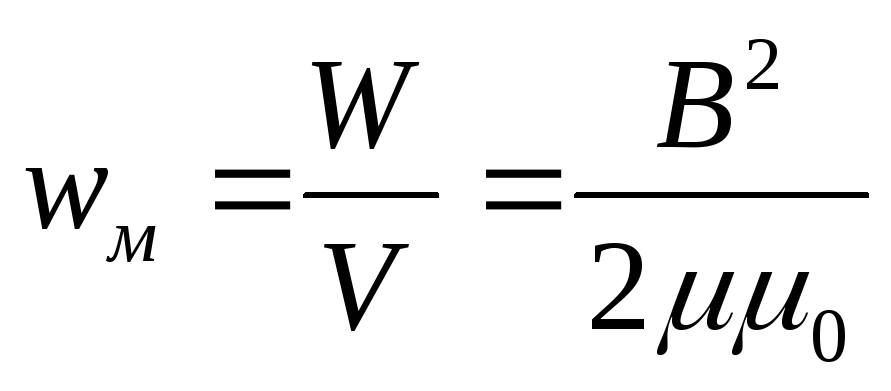 бъёмной
плотностью энергии называется энергия, заключённая в
единице объёма
бъёмной
плотностью энергии называется энергия, заключённая в
единице объёмаstudfile.net
Правило Ленца. Закон электромагнитной индукции . Видеоурок. Физика 11 Класс
На данном уроке, тема которого: «Правило Ленца. Закон электромагнитной индукции», мы узнаем общее правило, позволяющее определить направление индукционного тока в контуре, установленное в 1833 г. Э.X. Ленцем. Также рассмотрим опыт с алюминиевыми кольцами, наглядно демонстрирующий это правило, и сформулируем закон электромагнитной индукции
На прошлом уроке мы изучили явление электромагнитной индукции. Оно заключается в том, что при изменении магнитного потока, пронизывающего поверхность, которая ограничивается замкнутым токопроводящим контуром, в этом контуре возникает электрический ток. Также мы установили, что физический смысл скорости изменения магнитного потока – это электродвижущая сила индукции. При этом для расчета ЭДС электромагнитной индукции мы пользовались формулой:

В этой формуле стоит модуль, так как неизвестно направление индукционного тока. Именно вопросу нахождения направления индукционного тока посвящен этот урок.
Направление индукционного тока в контуре определяется правилом Ленца. Это правило устанавливается при помощи следующего опыта. Имеется два алюминиевых кольца, соединенных алюминиевой перекладиной. Одно из этих колец имеет разрез (не замкнутое), второе кольцо сплошное. Перекладина установлена на острие иглы, которая закреплена на подставке. Приближаем магнит к кольцу, имеющему разрез, – видно, что с системой ничего не происходит. При приближении магнита к замкнутому концу, система начинает поворачиваться (кольцо отталкивается от полюса магнита) (см. Рис. 1). Если же надеть кольцо на магнит и затем вытягивать магнит из него, то кольцо тянется за магнитом.

Рис. 1. Опыт Ленца (Источник)
Приближением или удалением магнита от сплошного кольца мы меняем магнитный поток, который пронизывает площадь кольца. Согласно теории явления электромагнитной индукции, в кольце должен возникнуть индукционный электрический ток. Из опытов Ампера известно, что там, где проходит ток, возникает магнитное поле. Следовательно, замкнутое кольцо начинает вести себя как магнит. То есть происходит взаимодействие двух магнитов (постоянный магнит, который мы двигаем, и замкнутый контур с током).
Так как система не реагировала на приближение магнита к кольцу с разрезом, то можно сделать вывод, что индукционный ток в незамкнутом контуре не возникает.
Причины отталкивания или притягивания кольца к магниту
1. При приближении магнита
При приближении полюса магнита кольцо отталкивается от него. То есть оно ведет себя как магнит, у которого с нашей стороны такой же полюс, как у приближающегося магнита. Если мы приближаем северный полюс магнита, то вектор магнитной индукции кольца с индукционным током направлен в противоположную сторону относительно вектора магнитной индукции северного полюса магнита (см. Рис. 2).
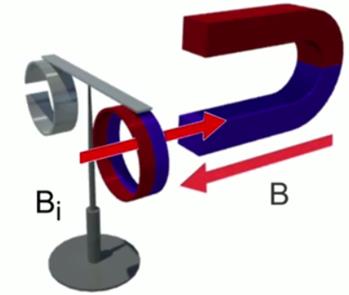
Рис. 2. Приближение магнита к кольцу
2. При удалении магнита от кольца
При удалении магнита кольцо тянется за ним. Следовательно, со стороны удаляющегося магнита у кольца образовывается противоположный полюс. Вектор магнитной индукции кольца с током направлен в ту же сторону, что и вектор магнитной индукции удаляющегося магнита (см. Рис. 3).
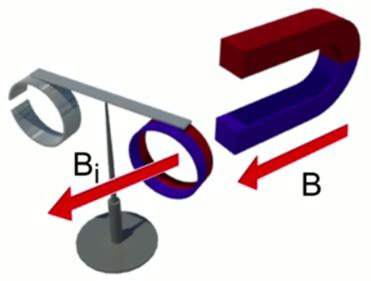
Рис. 3. Удаление магнита от кольца
Из данного опыта можно сделать вывод, что при движении магнита кольцо ведет себя также подобно магниту, полярность которого зависит от того, увеличивается или уменьшается магнитный поток, пронизывающий площадь кольца. Если поток возрастает, то векторы магнитной индукции кольца и магнита противоположны по направлению. Если магнитный поток сквозь кольцо уменьшается со временем, то вектор индукции магнитного поля кольца совпадает по направлению с вектором индукции магнита.
Направление индукционного тока в кольце можно определить по правилу правой руки. Если направить большой палец правой руки по направлению вектора магнитной индукции, то четыре согнутых пальца укажут направление тока в кольце (см. Рис. 4).
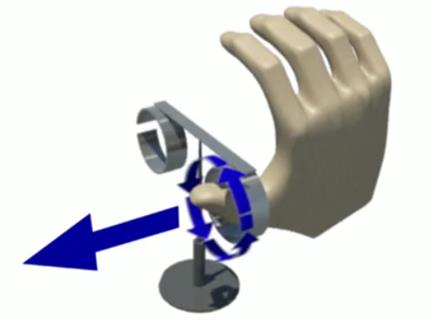
Рис. 4. Правило правой руки
При изменении магнитного потока, пронизывающего контур, в контуре возникает индукционный ток такого направления, чтобы своим магнитным потоком компенсировать изменение внешнего магнитного потока.
Закон электромагнитной индукции
Если внешний магнитный поток возрастает, то индукционный ток своим магнитным полем стремится замедлить это возрастание. Если магнитный поток убывает, то индукционный ток своим магнитным полем стремится замедлить это убывание.
Эта особенность электромагнитной индукции выражается знаком «минус» в формуле ЭДС индукции.
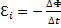
Закон электромагнитной индукции
При изменении внешнего магнитного потока, пронизывающего контур, в контуре возникает индукционный ток. При этом значение электродвижущей силы численно равно скорости изменения магнитного потока, взятой со знаком «-».
Правило Ленца является следствием закона сохранения энергии в электромагнитных явлениях.
Список литературы
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.
Домашнее задание
- Вопросы в конце параграфа 10 (стр. 33) – Мякишев Г.Я. Физика 11 (см. список рекомендованной литературы)
- Как формулируется закон электромагнитной индукции?
- Почему в формуле для закона электромагнитной индукции стоит знак «-»?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Festival.1september.ru (Источник).
- Интернет-портал Physics.kgsu.ru (Источник).
- Интернет-портал Youtube.com (Источник).
interneturok.ru
| Электромагнитная индукция | |
1831 г. — М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, — появление, возникновение). |
|
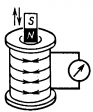
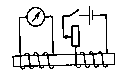
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи |
|
Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или: явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. |
|
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром. |
|
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы. |
|
Возникновение индукционного тока — следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: |
|
Источником магнитного поля является ток. Поэтому: Возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им поток магнитной индукции через площадь, ограниченную контуром, стремится компенсировать то изменение потока магнитной индукции, которое вызывает данный ток (правило Ленца). |
|
Ток в контуре имеет отрицательное направление ( Поэтому с учетом правила Ленца (знака) выражение для закона электромагнитной индукции записывается: Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой. |
|
Если контур (например, катушка) состоит из нескольких витков, то где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную: |
|
www.eduspb.com
Магнитный поток и ЭДС индукции
Продолжаем решать задачи на магнитный поток и ЭДС индукции. Здесь уже будет потяжелее: придется и производную, и первообразную находить. Но задачи интересные, и даже геометрические знания пригодились, а именно, формула площади треугольника.
Задача 1. Плоский замкнутый металлический контур площадью  см
см , находится в однородном магнитном поле, индукция которого
, находится в однородном магнитном поле, индукция которого  Тл. Площадь контура за время
Тл. Площадь контура за время  c равномерно уменьшается до
c равномерно уменьшается до  см
см (плоскость контура при этом остается перпендикулярной магнитному полю). Определите силу тока (в мкА), протекающего по контуру в течение времени
(плоскость контура при этом остается перпендикулярной магнитному полю). Определите силу тока (в мкА), протекающего по контуру в течение времени  , если сопротивление контура
, если сопротивление контура  Ом.
Ом.
![Rendered by QuickLaTeX.com \[E=-\frac{\Delta \Phi}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f54a0b8c1e483b4fa911275c90fb00f2_l3.png)
Поток уменьшился с  до
до  , его изменение
, его изменение  . Следовательно,
. Следовательно,
![Rendered by QuickLaTeX.com \[E =-\frac{ B(S_2-S_1)}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-88f22344a30da563ef0bb94d7abb48dd_l3.png)
Ток равен
![Rendered by QuickLaTeX.com \[I=\frac{E}{R}=\frac{ B(S_1-S_2)}{R\Delta t } =\frac{ 10^{-2} (10-2)\cdot10^{-4}}{1\cdot0,5}=16\cdot10^{-6}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dac238668f64a1f0faaa3f6b69f88bc1_l3.png)
Ответ: 16 мкА
Задача 2. Медное кольцо радиусом  см из проволоки диаметром
см из проволоки диаметром  мм расположено в однородном магнитном поле, изменяющемся со скоростью
мм расположено в однородном магнитном поле, изменяющемся со скоростью  Тл/с. Плоскость кольца перпендикулярна силовым линиям магнитного поля. Определите силу индукционного тока, возникающего в кольце. Удельное сопротивление меди равно
Тл/с. Плоскость кольца перпендикулярна силовым линиям магнитного поля. Определите силу индукционного тока, возникающего в кольце. Удельное сопротивление меди равно  Ом
Ом м.
м.
Сопротивление кольца равно
![Rendered by QuickLaTeX.com \[R=\frac{\rho l}{S}=\frac{\rho \cdot2 \pi R}{\frac{\pi d^2}{4}}=\frac{8\rho R}{d^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-daf76cbfc1cb2eaebca06b57f6aceef7_l3.png)
Ток в кольце будет равен
![Rendered by QuickLaTeX.com \[I=\frac{E}{R}=\frac{ \Delta \Phi}{R\Delta t } =\frac{\Delta B}{\Delta t}\cdot\frac{S}{R}=\frac{\Delta B}{\Delta t}\cdot \frac{\pi R^2 d^2}{8\rho}=0,2\cdot\frac{ \pi \cdot(0,15)^2\cdot(10^{-3})^2}{8\cdot1,7\cdot 10^{-8}}=0,693\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ab24d08ea36cc0583328f7d1675307a_l3.png)
Ответ: 0,693 А
Задача 3. При изменении силы тока в замкнутом контуре индуктивностью  Гн ЭДС самоиндукции изменялась согласно графику (см. рис.). Чему равна величина изменения тока в интервале времени 1-4 с?
Гн ЭДС самоиндукции изменялась согласно графику (см. рис.). Чему равна величина изменения тока в интервале времени 1-4 с?

К задаче 3
Так как
![Rendered by QuickLaTeX.com \[E=-L\frac{dI}{dt}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-75ff9d3d49a5001c7a8adbefc95bc7f4_l3.png)
То, чтобы найти ток, нужно найти интеграл. То есть – определить площадь под графиком с первой по 4 секунду. Площадь будет равна сумме площадей трапеции и прямоугольника: 3+8.
![Rendered by QuickLaTeX.com \[I=\int\limits_{1}^{4} \frac{E}{L}\, dt=\frac{11\cdot10^{-3}}{0,1}=0,11\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-08abc089a051c118c304ecdc0eed57d0_l3.png)
Ответ: 0,11 А
Задача 4. В однородном магнитном поле с индукцией В = 0,2 Тл начинает двигаться металлический стержень длиной  см перпендикулярно вектору магнитной индукции. Координата стержня изменяется по закону
см перпендикулярно вектору магнитной индукции. Координата стержня изменяется по закону  . Какая разность потенциалов возникает между концами стержня через 5 с?
. Какая разность потенциалов возникает между концами стержня через 5 с?
Скорость стержня к указанному моменту времени будет равна:
![Rendered by QuickLaTeX.com \[\upsilon=\frac{dx}{dt}=-3+4t=17\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-91517c625439a97b5c65d4cb64790471_l3.png)
Следовательно, ЭДС:
![Rendered by QuickLaTeX.com \[E=Bl\upsilon=0,2\cdot0,2\cdot17=0,68\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2435df5c221e2cfd5160b6c595f47366_l3.png)
Ответ: 0,68 В.
Задача 5. Проводящий квадратный контур со стороной  см, помещенный в однородное магнитное поле с индукцией В = 0,5 Тл, вектор которой перпендикулярен плоскости контура, складывают пополам (см. рис.). Какой заряд протечет по контуру, если сопротивление единицы длины контура равно
см, помещенный в однородное магнитное поле с индукцией В = 0,5 Тл, вектор которой перпендикулярен плоскости контура, складывают пополам (см. рис.). Какой заряд протечет по контуру, если сопротивление единицы длины контура равно  Ом/м?
Ом/м?

К задаче 5
Площадь контура, складывая его, уменьшают до нуля. Поэтому изменение потока равно  . Следовательно,
. Следовательно,
![Rendered by QuickLaTeX.com \[\frac{dq}{dt}\cdot R=\frac{d \Phi}{dt}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-554b057de677b5c01217106c7b6f6367_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[dq=\frac{ d \Phi }{R}=\frac{\Delta \Phi }{R}=\frac{BS}{R}=\frac{Bl^2}{4lr}=\frac{0,5\cdot0,1}{4\cdot0,1}=0,125\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-020bdfab184fd77ab9852cc92e199a39_l3.png)
Ответ: 0,125 Кл.
Задача 6. Напряжение на зажимах рамки, начинающей вращаться в однородном магнитном поле, изменяется с течением времени согласно графику на рисунке. Чему приблизительно равна величина магнитного потока, пересекающего рамку в момент времени  с?
с?

К задаче 7
Напряжение на зажимах, или ЭДС, есть производная потока, поэтому поток – первообразная ЭДС. ЭДС, судя по графику, можно записать так:
![Rendered by QuickLaTeX.com \[E=U=-U_m \cos(\omega t)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3f636afc7bc128c037f1e4f7383a9285_l3.png)
Период равен 4 с, тогда  . Амплитуда ЭДС равна 40 мВ, следовательно,
. Амплитуда ЭДС равна 40 мВ, следовательно,
![Rendered by QuickLaTeX.com \[E=-0,04 \cos(\frac{\pi t}{2})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f9c30d895fbac13ca7b01544ec48d95a_l3.png)
Определяем первообразную, то есть берем интеграл:
![Rendered by QuickLaTeX.com \[\Phi=\int\limits_{~}^{~} (-0,04 \cos(\frac{\pi t}{2}))\, dx=-0,04\frac{2}{\pi}\sin (\frac{\pi t}{2})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a6a2178adab11739ed5a2655b95b8c76_l3.png)
Подставим нужное время:
![Rendered by QuickLaTeX.com \[\Phi=-0,04\frac{2}{\pi}\sin (\frac{\pi \cdot2,5}{2}))=-0,04\frac{2}{\pi}\cdot \left(-\frac{\sqrt{2}}{2}\right)=17,8\cdot10^{-3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a06df7d5c65fc9a900589d58301f6f52_l3.png)
Ответ: 18 мВб.
Задача 7. Плоская проволочная рамка находится в магнитном поле, его плоскость перпендикулярна линиям индукции. При равномерном уменьшении магнитного поля до нуля за время  с в рамке возник постоянный ток
с в рамке возник постоянный ток  А. Какой ток
А. Какой ток  потечет по рамке при ее повороте в этом поле с постоянной угловой скоростью на угол
потечет по рамке при ее повороте в этом поле с постоянной угловой скоростью на угол  за время
за время  с вокруг оси, перпендикулярной вектору В и лежащей в плоскости рамки?
с вокруг оси, перпендикулярной вектору В и лежащей в плоскости рамки?
И в том, и в другом случае меняется поток через рамку. Но индукция поля остается неизменной, ее–то и надо найти:
![Rendered by QuickLaTeX.com \[I_1=\frac{\Delta \Phi_1}{Rt_1}=\frac{\Delta B S}{Rt_1}=\frac{B S}{Rt_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2ae8094cd6622c15ae6e2a5837f4b206_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[B=\frac{ I_1Rt_1 }{S}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8aa3a2a508667bca47efe1bfce06497c_l3.png)
Если рамку повернуть, то изменится площадь, пронизываемая потоком:
![Rendered by QuickLaTeX.com \[S_2=S\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ebf1413314e66e4af12d86c08b8653ef_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[I_2=\frac{\Delta \Phi_2}{Rt_2}=\frac{\Delta S B }{Rt_2}=\frac{B S\cos{\alpha}}{Rt_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cdb182a56f8ca6761d0829258dcb435f_l3.png)
Подставим индукцию, найденную ранее:
![Rendered by QuickLaTeX.com \[I_2=\frac{ S\cos{\alpha}}{Rt_2}\cdot \frac{ I_1Rt_1 }{S}=\frac{I_1t_1\cos{\alpha}}{t_2}=\frac{0,024\cdot2\cdot0,5}{4}=0,006\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b0537e12550adac28ec0e200ce92f6e2_l3.png)
Ответ: 6 мА.
Задача 8. Квадратная рамка со стороной  см помещена в однородное магнитное поле с индукцией
см помещена в однородное магнитное поле с индукцией  мТл так, что линии индукции перпендикулярны плоскости рамки (см. рис.). Сопротивление рамки 1 Ом. Какое количество тепла выделится в рамке за 10 с, если ее выдвигать из области, в которой создано поле со скоростью 1 см/с, перпендикулярной линиям индукции? Поле сосредоточено в некоторой четко ограниченной области.
мТл так, что линии индукции перпендикулярны плоскости рамки (см. рис.). Сопротивление рамки 1 Ом. Какое количество тепла выделится в рамке за 10 с, если ее выдвигать из области, в которой создано поле со скоростью 1 см/с, перпендикулярной линиям индукции? Поле сосредоточено в некоторой четко ограниченной области.

К задаче 8
Площадь рамки, помещенная в поле, будет изменяться. Поэтому поток меняется и в рамке наводится ЭДС.
![Rendered by QuickLaTeX.com \[E=Bl\upsilon\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5b64c9507b07a80fcad547d3f78067ff_l3.png)
Ток будет равен:
![Rendered by QuickLaTeX.com \[I=\frac{E}{R}=\frac{ Bl\upsilon }{R}=\frac{0,1\cdot0,02\cdot 0,01}{1}=2\cdot10^{-5}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab01e6f626c74af4d6d7abd68464a158_l3.png)
При протекании такого тока выделится количество теплоты
![Rendered by QuickLaTeX.com \[Q=I^2Rt=(2\cdot10^{-5})^2\cdot 1\cdot 10=8\cdot10^{-10}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-71c0819c65e812564bd710f1516af3f4_l3.png)
Ответ: 0,8 нДж
Задача 9. Квадратная рамка помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с направлением магнитного поля угол  . Сторона рамки
. Сторона рамки  см. Известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение времени
см. Известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении поля в течение времени  с, равно 50 мВ. С какой силой подействовало бы это магнитное поле на протон, влетевший в него со скоростью
с, равно 50 мВ. С какой силой подействовало бы это магнитное поле на протон, влетевший в него со скоростью  м/с перпендикулярно вектору
м/с перпендикулярно вектору  ?
?
 . Следовательно,
. Следовательно,
![Rendered by QuickLaTeX.com \[E=\frac{\Delta\Phi}{\Delta t}=\frac{BS_r}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8b0f846e0a81f9a59ed558f9f638c3b9_l3.png)
Пронизываемая потоком площадь рамки равна
![Rendered by QuickLaTeX.com \[S_r=S\cos{\alpha}=L^2\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8bbca4d2f2e744f3b99235db2a2bcd24_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[E=\frac{BL^2\cos{\alpha}}{\Delta t }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1b4459348dd0efeb29ee05f8606e3a76_l3.png)
Найдем из этого выражения индукцию поля:
![Rendered by QuickLaTeX.com \[B=\frac{E\Delta t }{ L^2\cos{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a92eae5023a908373ce80270eb40b7c2_l3.png)
Сила Лоренца равна
![Rendered by QuickLaTeX.com \[F=B q \upsilon=\frac{E\Delta t q \upsilon }{ L^2\cos{\alpha}}=\frac{50\cdot10^{-3}\cdot0,01\cdot1,6\cdot10^{-19}\cdot10^4}{ (0,1)^2\cdot0,5}=1,6\cdot10^{-16}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-df4cc0e10f14aa4a4abb4f3fa1da690f_l3.png)
Ответ:  Н.
Н.
Задача 10. Рамка сопротивлением 15 Ом, имеющая форму равностороннего треугольника, помещена в однородное магнитное поле с индукцией  Тл. Плоскость рамки составляет с направлением вектора
Тл. Плоскость рамки составляет с направлением вектора  угол
угол  . Определите длину стороны рамки
. Определите длину стороны рамки  , если при равномерном уменьшении индукции В до нуля в течение
, если при равномерном уменьшении индукции В до нуля в течение  с в проводнике рамки выделяется количество тепла 0,5 мДж.
с в проводнике рамки выделяется количество тепла 0,5 мДж.
По закону Джоуля-Ленца
![Rendered by QuickLaTeX.com \[Q=I^2Rt\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-edea0d3a0e8be89363e774d449ad944d_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[I=\sqrt{\frac{Q}{Rt}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-563efd2de4a6f5727d782c2666ac7fe3_l3.png)
По закону Ома  ,
,
![Rendered by QuickLaTeX.com \[E=\sqrt{\frac{QR}{t}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e3407b6c3bafac6ca6517939de27846d_l3.png)
Площадь рамки равна  , площадь, пронизываема потоком, равна
, площадь, пронизываема потоком, равна
![Rendered by QuickLaTeX.com \[S_B=\frac{1}{2}a^2 \sin^2{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-85be45b81a4d3b39878916cce3a8adf5_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[E=\frac{BS}{t}=\frac{B}{2t}a^2 \sin^2{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4a8507d872fcbb56c080ba22df7c7aab_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[a^2=\frac{2Et}{B\sin^2{\alpha}}=\frac{2\sqrt{QRt}}{B\sin^2{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2f5f800fc77ac271b7a9c046a990023f_l3.png)
![Rendered by QuickLaTeX.com \[a=\frac{1}{\sin{\alpha}}\sqrt{\frac{2\sqrt{QRt}}{B}}=\frac{1}{\sin{\alpha}}\sqrt[4]{\frac{4QRt}{B^2}}=\frac{2}{\sqrt{3}}\sqrt[4]{\frac{4\cdot0,5\cdot10^{-3}\cdot15\cdot0,03}{0,04^2}}=0,76\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7033aae39a9a1d996124ab29d420fd31_l3.png)
Ответ : м.
м.
easy-physic.ru
Явление э/м индукции. Магн. поток. Закон э/м индукции
- Явление электромагнитной индукции
Электрические и магнитные поля порождаются одними и теми же источниками – электрическими зарядами, поэтому можно предположить, что между этими полями существует определенная связь. Это предположение нашло экспериментальное подтверждение в 1831 г. в опытах выдающегося английского физика М.Фарадея. Он открыл явление электромагнитной индукции.
Явление электромагнитной индукции лежит в основе работы индукционных генераторов электрического тока, на которые приходится вся вырабатываемая в мире электроэнергия.
- Магнитный поток
Количественной характеристикой процесса изменения магнитного поля через замкнутый контур является физическая величина называемая магнитным потоком. Магнитным потоком (Ф) через замкнутый контур площадью (S) называют физическую величину, равную произведению модуля вектора магнитной индукции (В) на площадь контура (S) и на косинус угла между вектором В и нормалью к поверхности: Φ = BS cos α. Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 Тл · 1 м2.
Если вектор магнитной индукции перпендикулярен площади контура, то магнитный поток максимальный.
Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.
- Закон электромагнитной индукции
Опытным путем был установлен закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром: Эта формула носит название закона Фарадея.
Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея. В нем, чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.
- Правило Ленца
Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский физик Э.Х.Ленц. Согласно правилу Ленца, возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Более кратко это правило можно сформулировать следующим образом: индукционный ток направлен так, чтобы препятствовать причине, его вызывающей. Правило Ленца отражает тот экспериментальный факт, что всегда имеют противоположные знаки (знак «минус» в формуле Фарадея).
Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине. Они могли вращаться вокруг оси, как коромысло. При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца оно стремилось «догнать» магнит. При движении же магнита внутри разрезанного кольца никакого движения не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
kaplio.ru
Электромагнитная индукция
Закон электромагнитной индукции.Правило Ленца. В 1831 году Фарадей
сделал одно из самых фундаментальных
открытий в электродинамике и физике в
целом – явление электромагнитной
индукции: в замкнутом проводящем контуре
при изменении магнитного потока (т.е.
потока вектора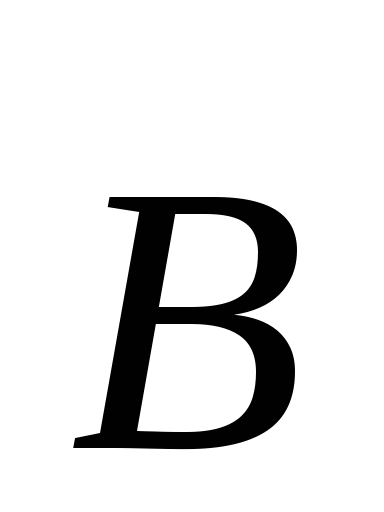 ),
охватываемого этим контуром, возникает
электрический ток, называемый индукционным.
),
охватываемого этим контуром, возникает
электрический ток, называемый индукционным.
Появление индукционного тока означает, что при изменении магнитного потока в контуре возникает эдсиндукцииƐi . Направление индукционного тока в контуре подчиняется следующемуправилу Ленца:индукционный ток направлен так, чтобы противодействовать своим магнитным полем вызывающей его причине.
Математическая формулировка закона электромагнитной индукции Фарадея-Ленца:
Ɛi= 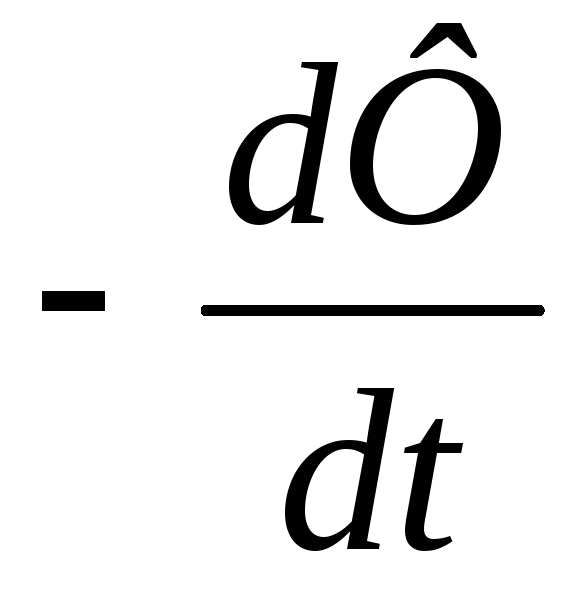 . (97)
. (97)
П ри
изменении потока магнитной индукции
через замкнутый контур в последнем
возникаетэдсиндукции,
пропорциональная скорости изменения
магнитного потока через поверхность,
ограниченную этим контуром. Знак
минус в (97) связан с правилом Ленца: если
поток растет, то магнитное поле
индукционного тока направлено так,
чтобы суммарный поток уменьшался, а
если поток уменьшается, то — чтобы
увеличивался.
ри
изменении потока магнитной индукции
через замкнутый контур в последнем
возникаетэдсиндукции,
пропорциональная скорости изменения
магнитного потока через поверхность,
ограниченную этим контуром. Знак
минус в (97) связан с правилом Ленца: если
поток растет, то магнитное поле
индукционного тока направлено так,
чтобы суммарный поток уменьшался, а
если поток уменьшается, то — чтобы
увеличивался.
Закон электромагнитной индукции
является одним из постулатов
электродинамики. Однако можно понять
природу этого явления из следующего
примера, который ни в коем случае нельзя
рассматривать как вывод самого закона.
Пусть тонкий проводящий контур с
подвижной перемычкой abдлиныlпомещен в
магнитное поле, направленное перпендикулярно
рис. 34, от нас. Начнем двигать перемычку
(вместе со всеми находящимися в ней
свободными электронами) вправо со
скоростью  .
В результате на каждый электрон начнет
действовать магнитная сила Лоренца
.
В результате на каждый электрон начнет
действовать магнитная сила Лоренца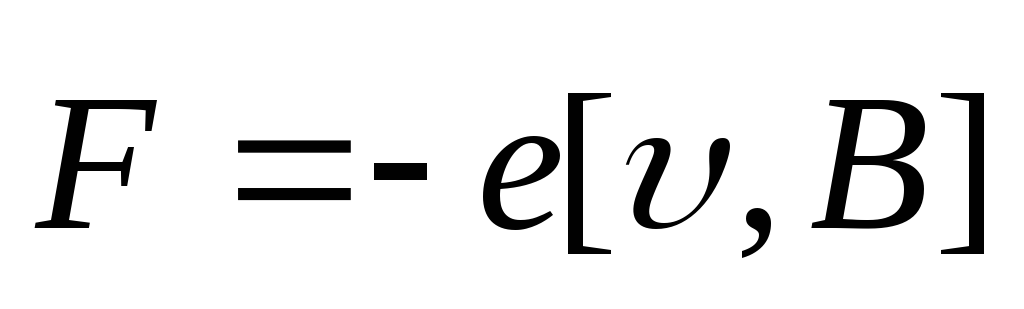 ,
направленная вниз вдоль перемычки –
потечет ток формально направленный
вверх (за направление плотности тока
принимается скорость направленного
движенияположительныхзарядов,
что эквивалентно движениюэлектроновв противоположном направлении). В данном
случае сила Лоренца играет роль сторонней
силы электрического поля с напряженностью
,
направленная вниз вдоль перемычки –
потечет ток формально направленный
вверх (за направление плотности тока
принимается скорость направленного
движенияположительныхзарядов,
что эквивалентно движениюэлектроновв противоположном направлении). В данном
случае сила Лоренца играет роль сторонней
силы электрического поля с напряженностью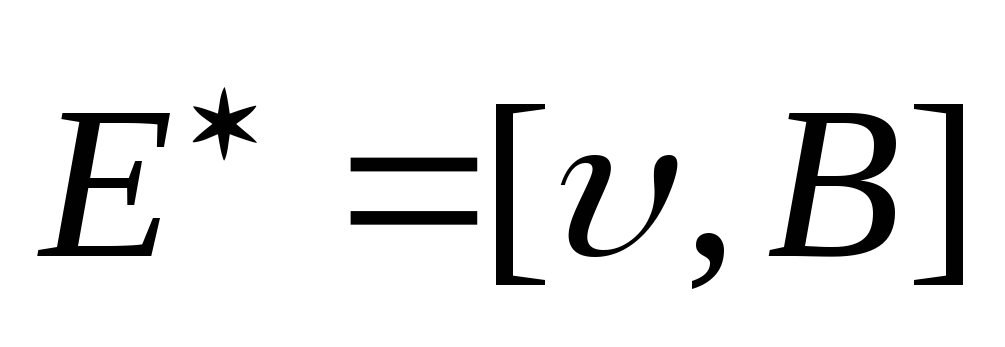 .
По определению (37) циркуляция поля
.
По определению (37) циркуляция поля дает величинуэдсиндукцииƐi,
в данном случае
дает величинуэдсиндукцииƐi,
в данном случае
Ɛi=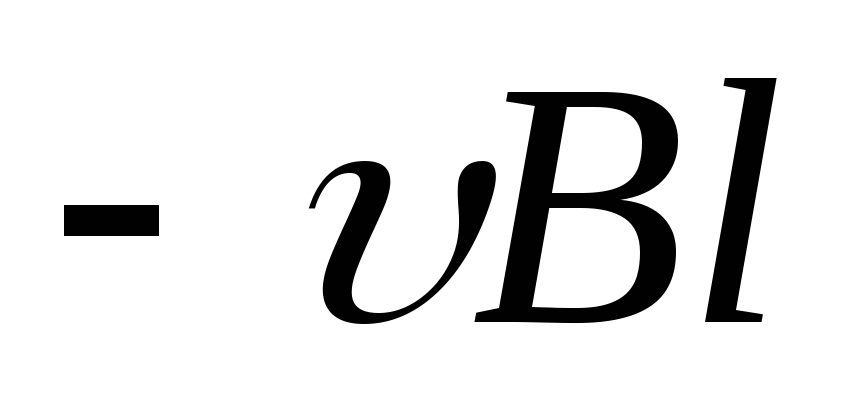 . (98)
. (98)
Минус – из-за того, что при данном
направлении вектора 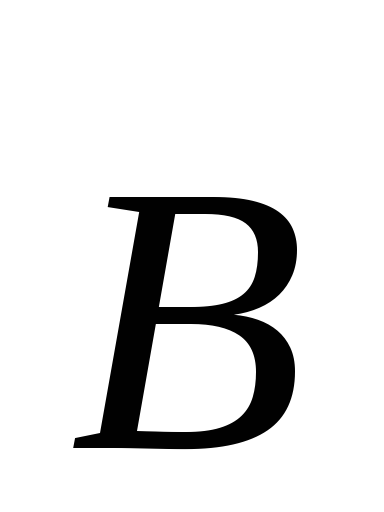 положительное направление обхода
контура по часовой стрелке. Произведение
положительное направление обхода
контура по часовой стрелке. Произведение есть приращение площади контура в
единицу времени (
есть приращение площади контура в
единицу времени ( ),
поэтому
),
поэтому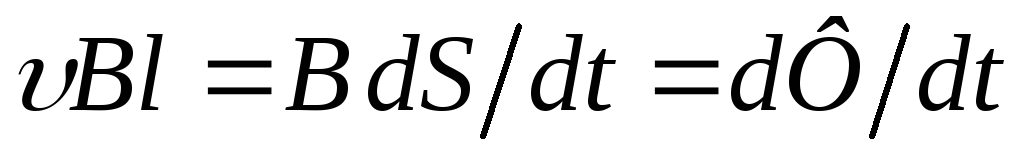 ,
где
,
где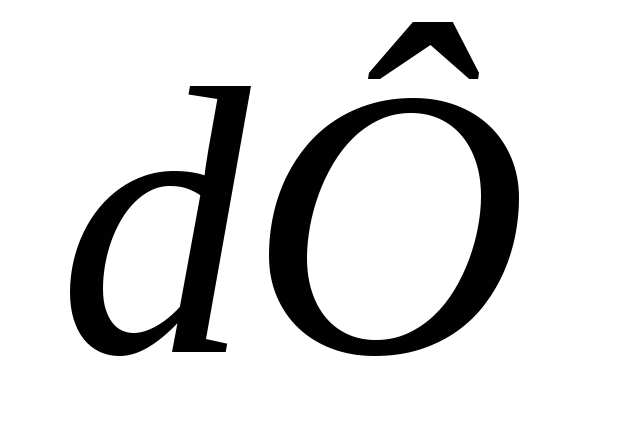 >
0 – приращение магнитного потока сквозь
площадь контура. Таким образом,Ɛi =
>
0 – приращение магнитного потока сквозь
площадь контура. Таким образом,Ɛi =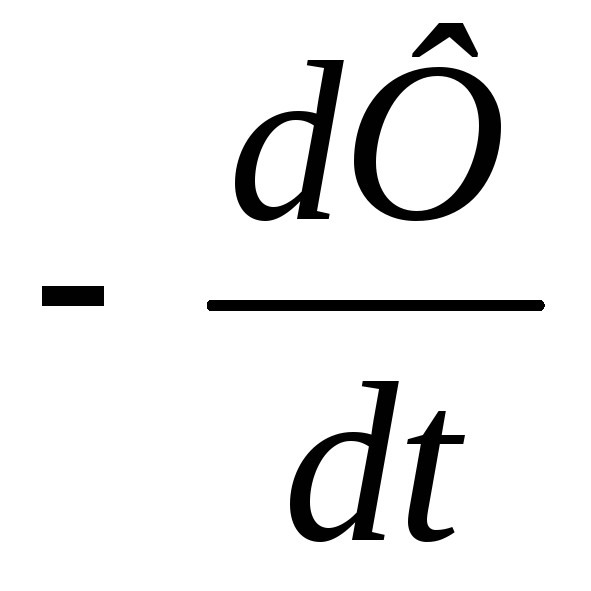 .
.
Явление самоиндукции.Индуктивность. Явление
электромагнитной индукции возникает
в замкнутом проводящем контуре независимо
от того, чем вызвано изменение магнитного
потока. В частности, изменение магнитного
потока может быть вызвано изменением
тока в этом же контуре. В этом случае
явление называютсамоиндукцией,
а соответствующую величинуƐs– эдс самоиндукции. Если в пространстве,
где находится контур с током ,
нет ферромагнетиков, то в соответствии
с законом Био-Саварра поле вектора
,
нет ферромагнетиков, то в соответствии
с законом Био-Саварра поле вектора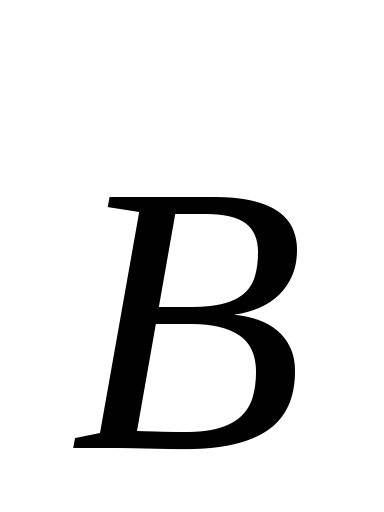 ,
а следовательно, и полный магнитный
потокФбудут пропорциональны силе
тока
,
а следовательно, и полный магнитный
потокФбудут пропорциональны силе
тока
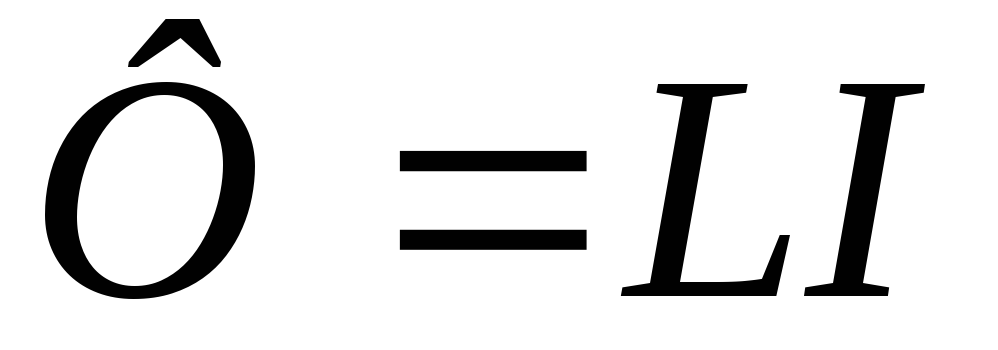 , (99)
, (99)
где L– коэффициент, называемыйиндуктивностьюконтура. ИндуктивностьLзависит от формы и размеров контура, а также от магнитных свойств окружающей среды. Если контур жесткий и вблизи нет ферромагнетиков, индуктивность является величиной постоянной.
 Если
в проводящем контуре изменяется ток,
то по закону электромагнитной индукции
в нем возникаетэдссамоиндукцииƐs=
Если
в проводящем контуре изменяется ток,
то по закону электромагнитной индукции
в нем возникаетэдссамоиндукцииƐs=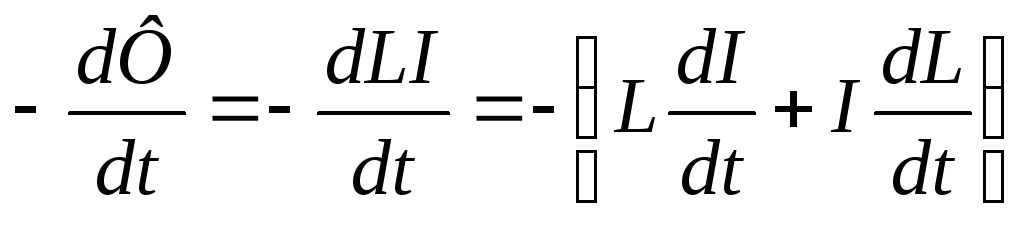 .
Если индуктивностьLпостоянна для данного контура, второе
слагаемое в скобках равно нулю, и тогда
.
Если индуктивностьLпостоянна для данного контура, второе
слагаемое в скобках равно нулю, и тогда
Ɛs=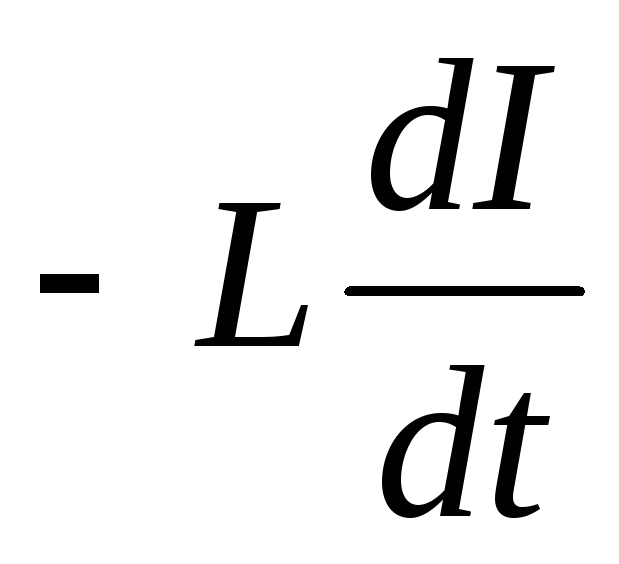 , (100)
, (100)
где минус обусловлен правилом Ленца:
если основной ток  в контуре возрастает, то индукционный
направлен в противоположную сторону
(рис.35 a). Если
основной ток
в контуре возрастает, то индукционный
направлен в противоположную сторону
(рис.35 a). Если
основной ток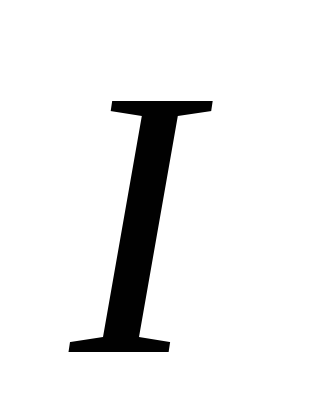 в контуре убывает, то индукционный
направлен в ту же сторону (рис.35 b).
в контуре убывает, то индукционный
направлен в ту же сторону (рис.35 b).
Индуктивность соленоида. При
прохождении тока по
длинному соленоиду, внутри которого
находится магнетик с магнитной
проницаемостью,
в последнем возникает магнитное поле
(60), равное
по
длинному соленоиду, внутри которого
находится магнетик с магнитной
проницаемостью,
в последнем возникает магнитное поле
(60), равное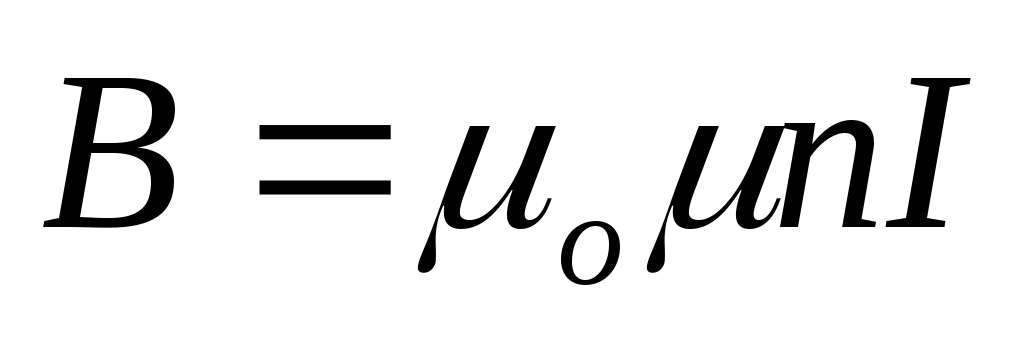 .
Пусть соленоид имеет площадь поперечного
сеченияSи полное
число витковN. Тогда
поток сквозь каждый витокФ=ВS,
а полный поток, сцепленный с соленоидом,
.
Пусть соленоид имеет площадь поперечного
сеченияSи полное
число витковN. Тогда
поток сквозь каждый витокФ=ВS,
а полный поток, сцепленный с соленоидом,
NФ=NВS=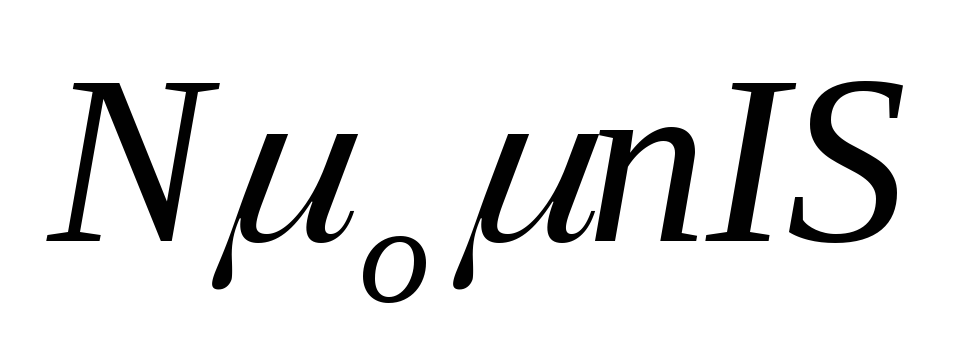 .
Так как
.
Так как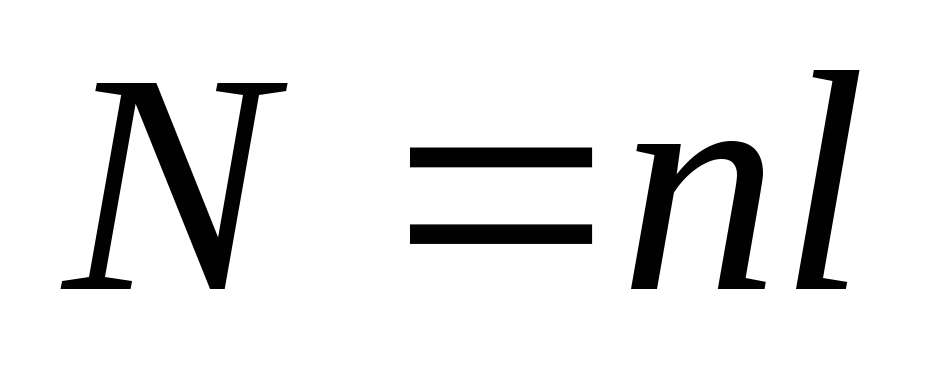 ,
где
,
где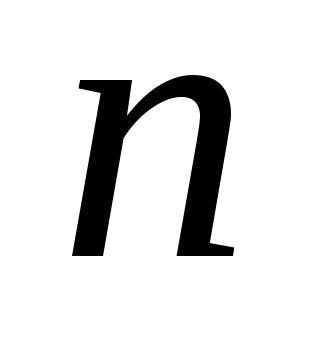 — число витков на единицу длины,
— число витков на единицу длины, —
длина соленоида, тоNФ=
—
длина соленоида, тоNФ=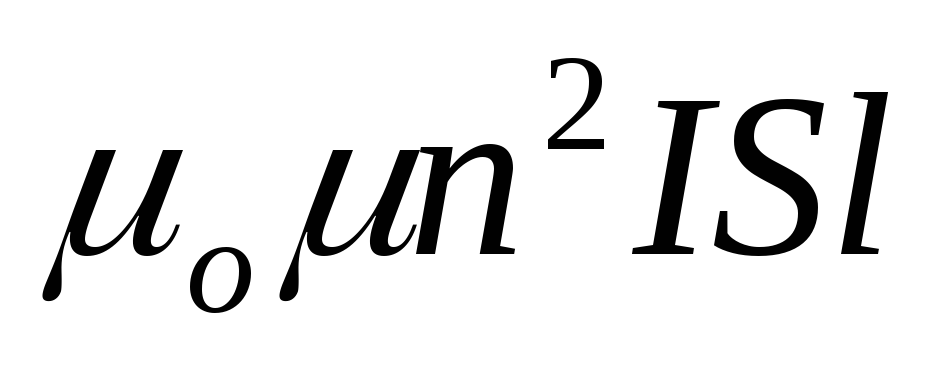 =
=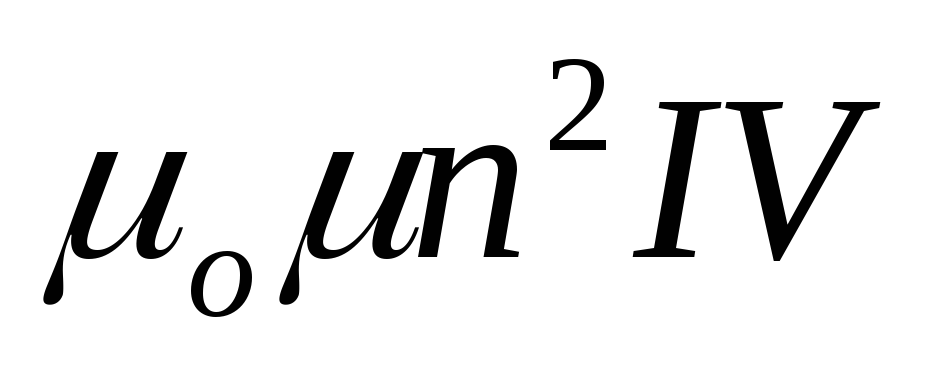 (
(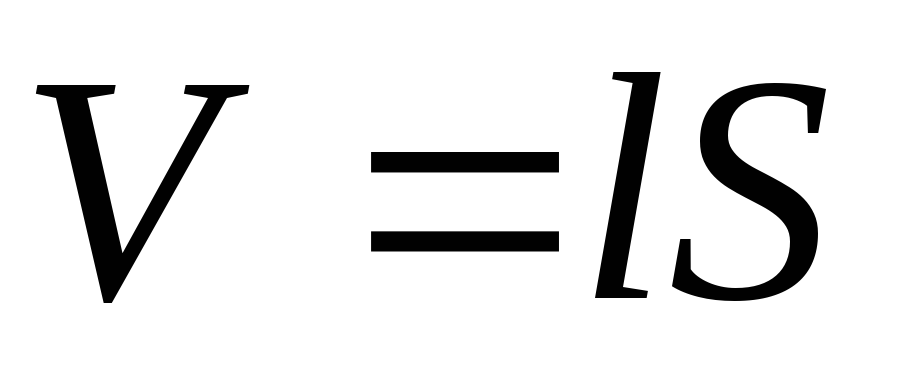 —
объем соленоида). Следовательно,
индуктивность соленоида, согласно ее
определению (99) равна
—
объем соленоида). Следовательно,
индуктивность соленоида, согласно ее
определению (99) равна 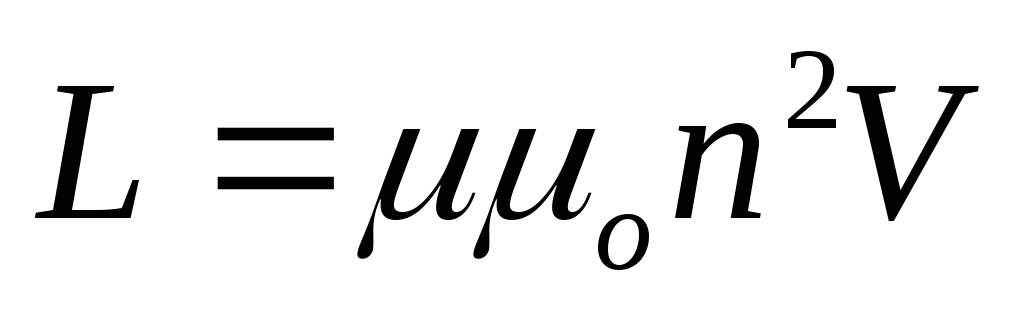 .
.
Взаимная индукция. Пусть два
неподвижных контура расположены близко
друг к другу. Если в контуре 1 течет ток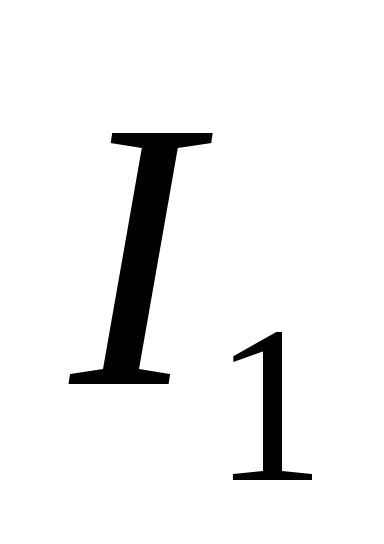 ,
он создает через контур 2 полный магнитный
потокФ2, пропорциональный
току
,
он создает через контур 2 полный магнитный
потокФ2, пропорциональный
току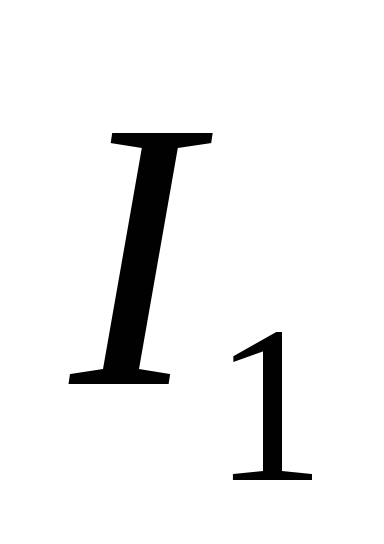
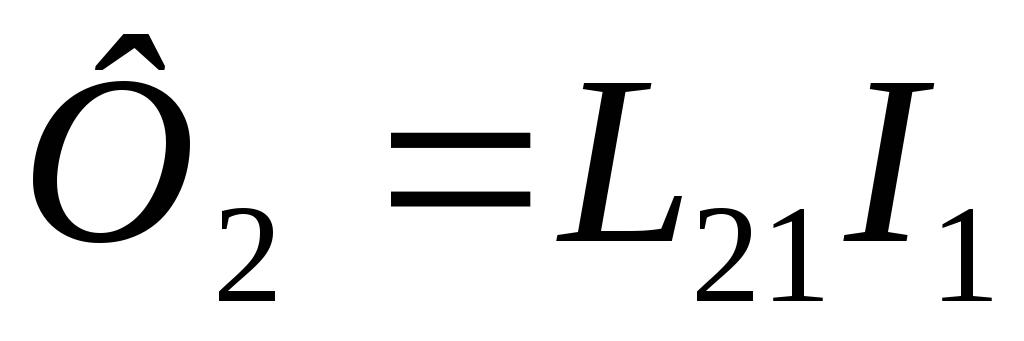 . (101)
. (101)
Так же, если в контуре 2 течет ток 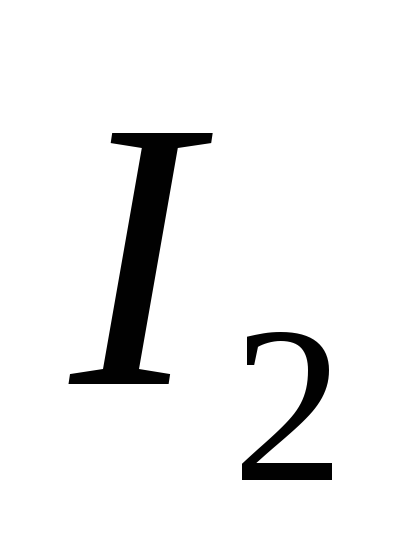 ,
он создает через контур 1 полный магнитный
потокФ1
,
он создает через контур 1 полный магнитный
потокФ1
 . (102)
. (102)
Коэффициенты 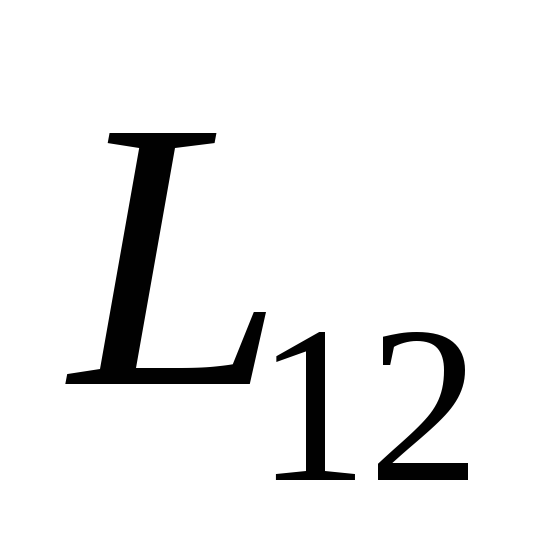 и
и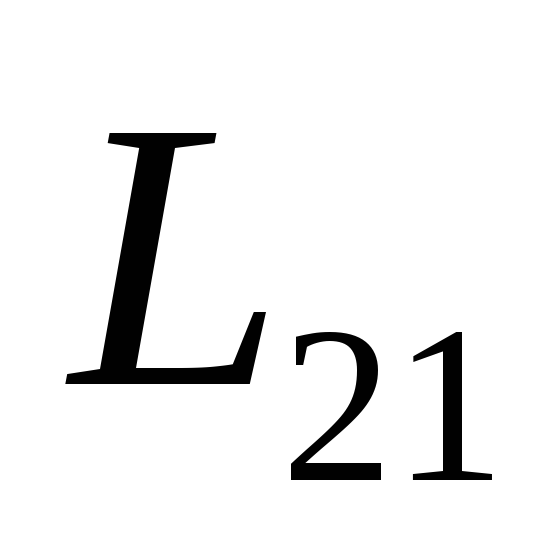 называютвзаимной индуктивностьюконтуров. Расчет и опыт показывают, чтокоэффициенты взаимной индуктивности
одинаковы при отсутствии ферромагнетиков
называютвзаимной индуктивностьюконтуров. Расчет и опыт показывают, чтокоэффициенты взаимной индуктивности
одинаковы при отсутствии ферромагнетиков
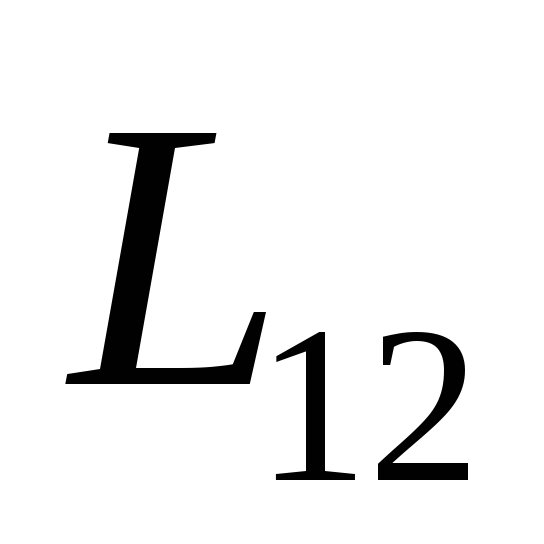 =
=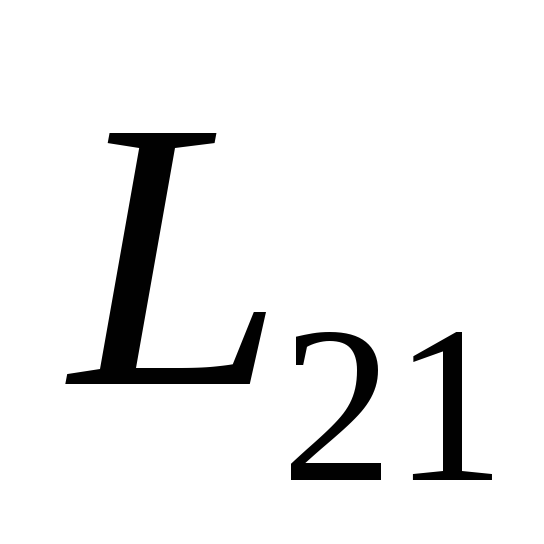 . (103)
. (103)
Это равенство принято называть теоремой взаимности. Наличие магнитной связи между контурами проявляется в том, что при всяком изменении тока в одном из них в другом возникаетэдсиндукции. Это явление называютвзаимной индукцией. Согласно закону электромагнитной индукцииэдс, возникающие в контурах 1 и 2, можно выразить так
Ɛ1=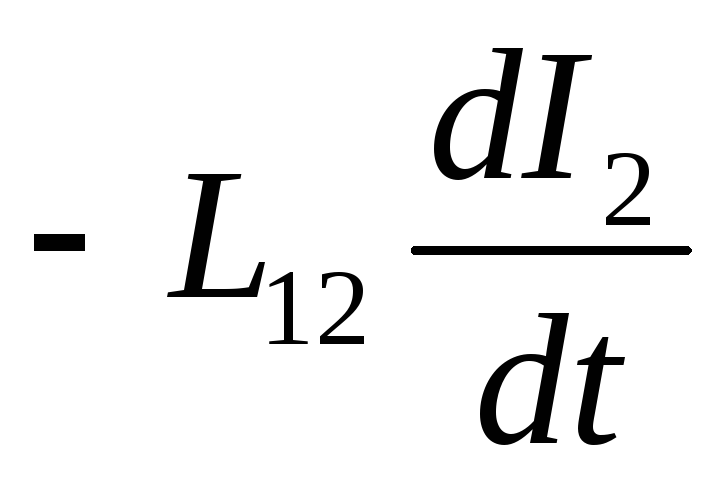 ; Ɛ2=
; Ɛ2= . (104)
. (104)
Трансформатор. Пусть две катушки
с числами витков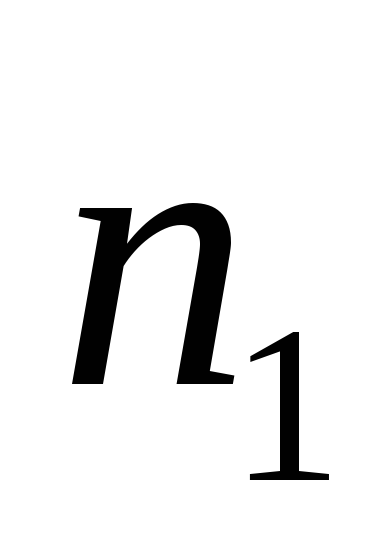 и
и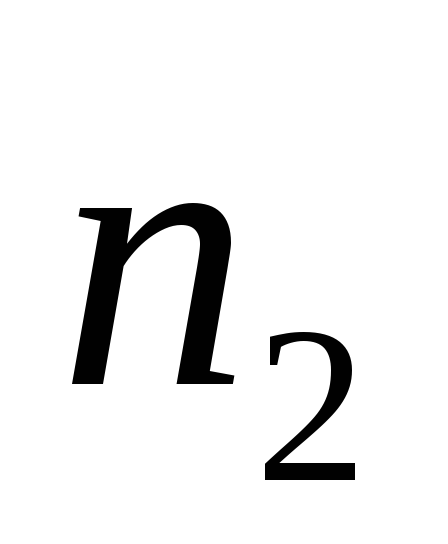 намотаны на общий сердечник. Собственно
это и есть трансформатор. Он служит для
повышения или понижения напряжения.
Поскольку магнитное поле в этом случае
сосредоточено главным образом в
сердечнике, то число линий вектора
намотаны на общий сердечник. Собственно
это и есть трансформатор. Он служит для
повышения или понижения напряжения.
Поскольку магнитное поле в этом случае
сосредоточено главным образом в
сердечнике, то число линий вектора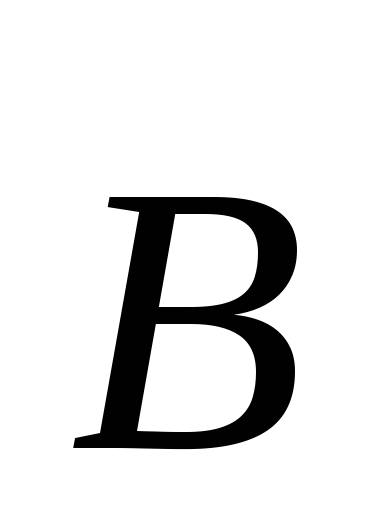 ,
а также и величина
,
а также и величина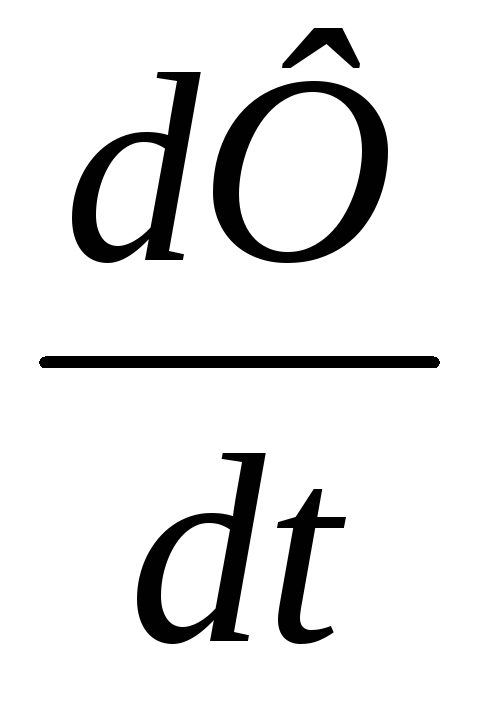 для обеих катушек будет одинаковым.
Считая, что поток пронизывает
для обеих катушек будет одинаковым.
Считая, что поток пронизывает витков первой катушки и
витков первой катушки и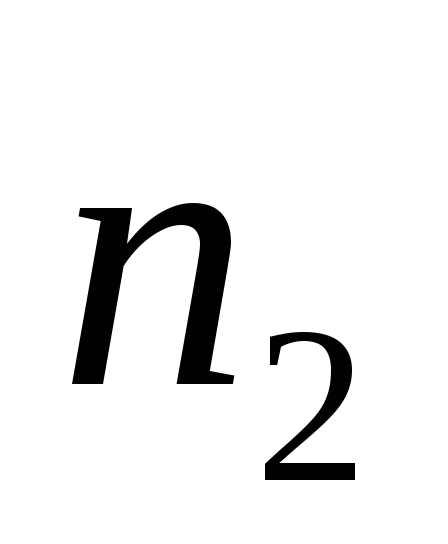 — второй, запишем соответствующиеэдс
— второй, запишем соответствующиеэдс
Ɛ1=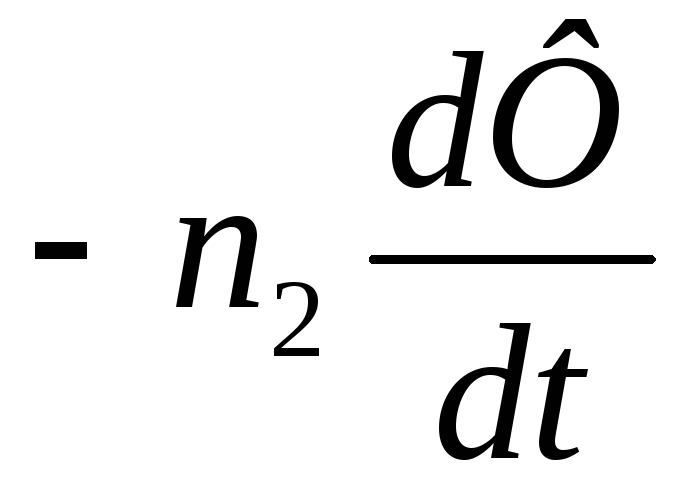 ; Ɛ2=
; Ɛ2= . (105)
. (105)
О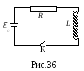 тношениеэдсравно
тношениеэдсравно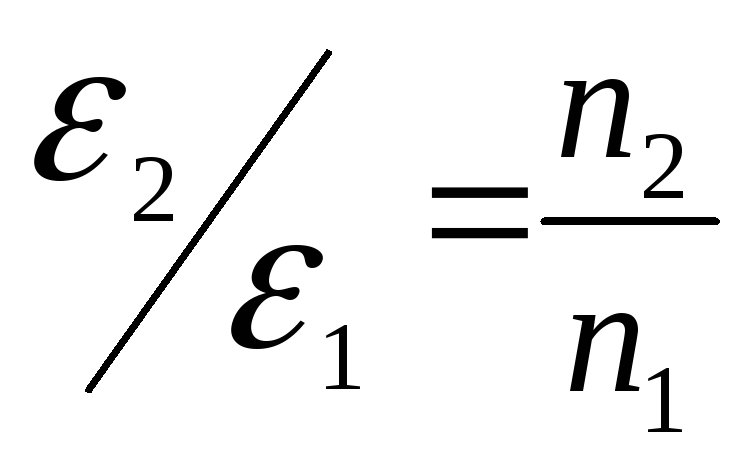 .
Если считать, что к первой обмотке
приложенаƐ1~
.
Если считать, что к первой обмотке
приложенаƐ1~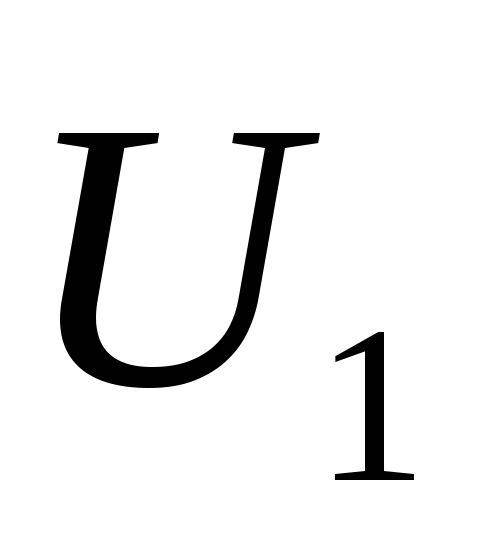 ,
то изменяя число витков
,
то изменяя число витков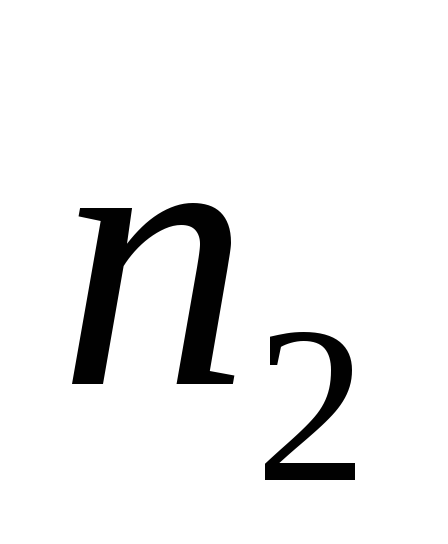 во второй катушке, во второй обмотке
можно получить повышенное или пониженное
напряжение
во второй катушке, во второй обмотке
можно получить повышенное или пониженное
напряжение  .
.
Энергия магнитного поля. Замкнем
цепь, содержащую индуктивностьL и сопротивлениеR на источник сэдсℇо.
В контуре начнет возрастать ток,
что приведет к появлениюэдссамоиндукцииƐs.
По закону Ома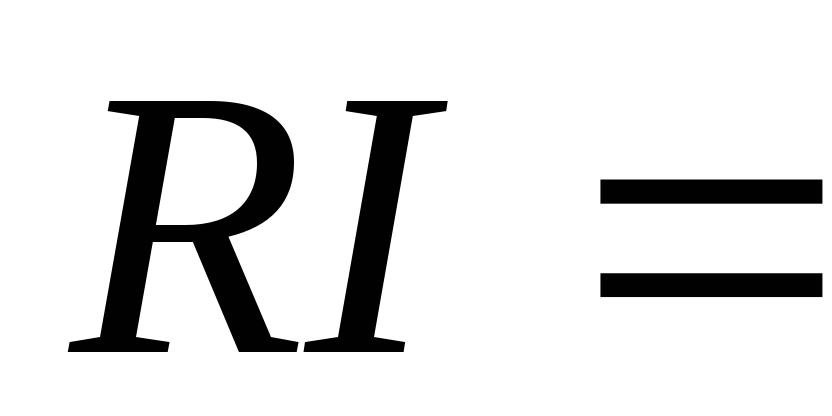 ℇо + Ɛs,ℇо =
ℇо + Ɛs,ℇо =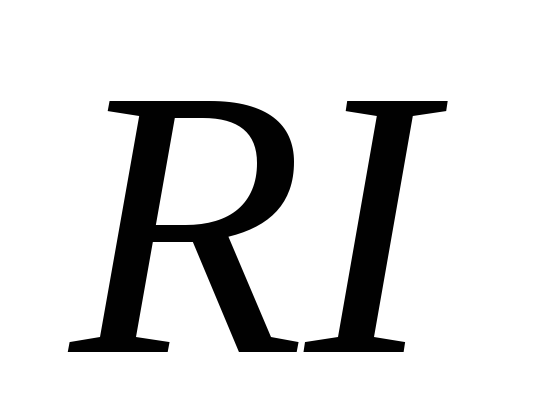 — Ɛs.
Источник сэдсℇо за времяdtсовершит
работуℇоIdt.
Умножим выражение в рамке наIdt
— Ɛs.
Источник сэдсℇо за времяdtсовершит
работуℇоIdt.
Умножим выражение в рамке наIdt
ℇоIdt=RI2dt—ƐsIdt.
Выражение RI2dt=δQ это джоулева теплота, а последнее
слагаемое (-ƐsIdt=IdФ), так как по
закону электромагнитной индукцииƐs=-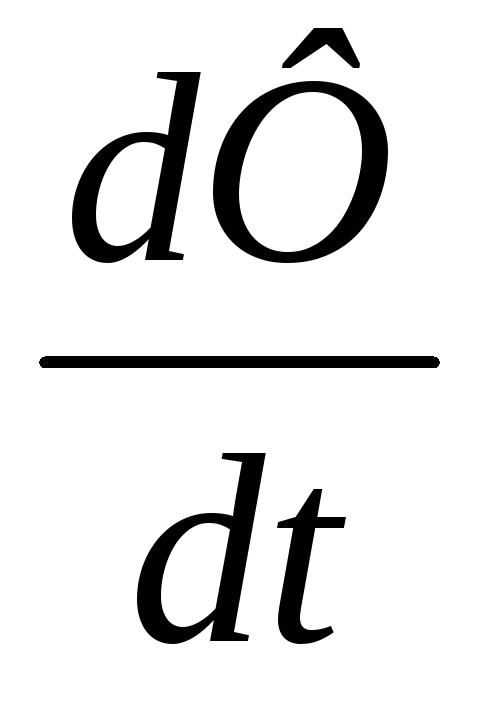 . Из этого следует, что работа, которую
совершает источник, больше, чем
выделяющаяся теплота. Часть этой работы
(IdФ) совершается
противэдссамоиндукции и идет на
увеличение энергии магнитного поля
катушки индуктивности (соленоида). Так
как
. Из этого следует, что работа, которую
совершает источник, больше, чем
выделяющаяся теплота. Часть этой работы
(IdФ) совершается
противэдссамоиндукции и идет на
увеличение энергии магнитного поля
катушки индуктивности (соленоида). Так
как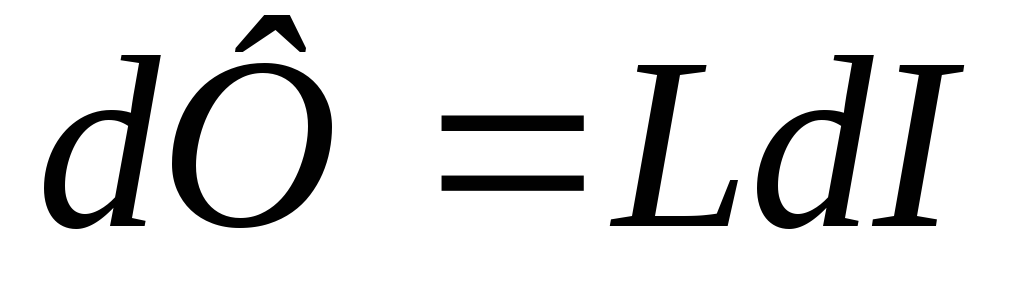 ,
,
 . (106)
. (106)
Поскольку индуктивность соленоида 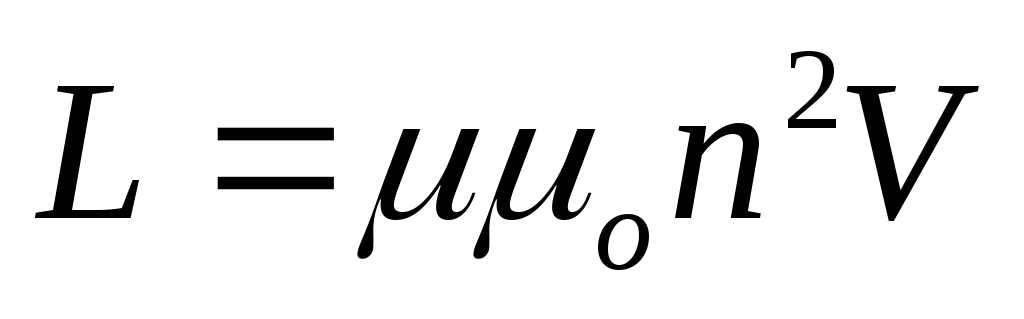 ,
а индукция его магнитного поля
,
а индукция его магнитного поля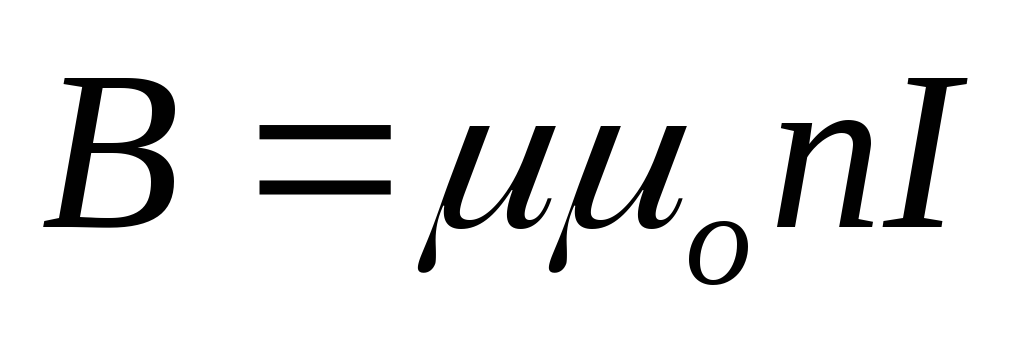 ,
то энергию магнитного поля можно выразить
как
,
то энергию магнитного поля можно выразить
как
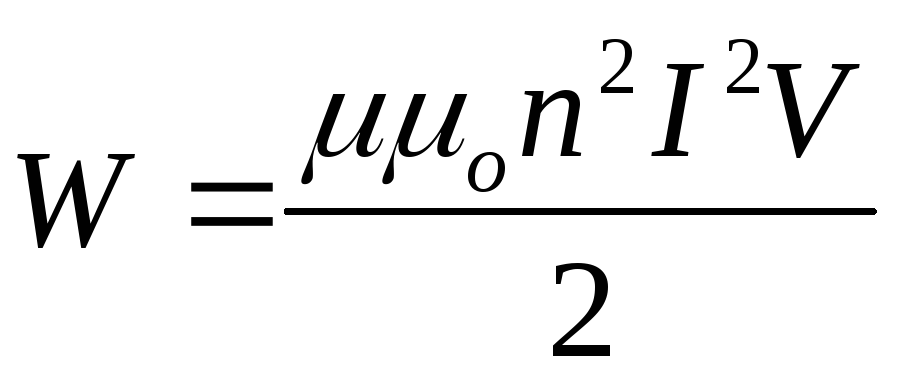 =
= =
= . (107)
. (107)
Мы учли, что 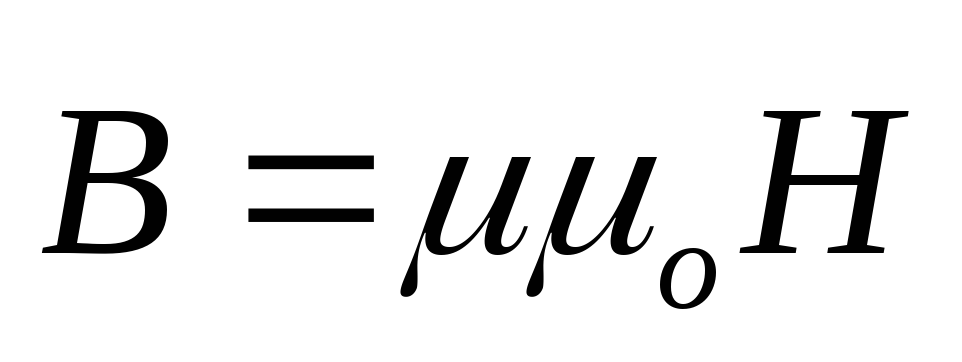 (92), или, в данном случае однородного
поля соленоида
(92), или, в данном случае однородного
поля соленоида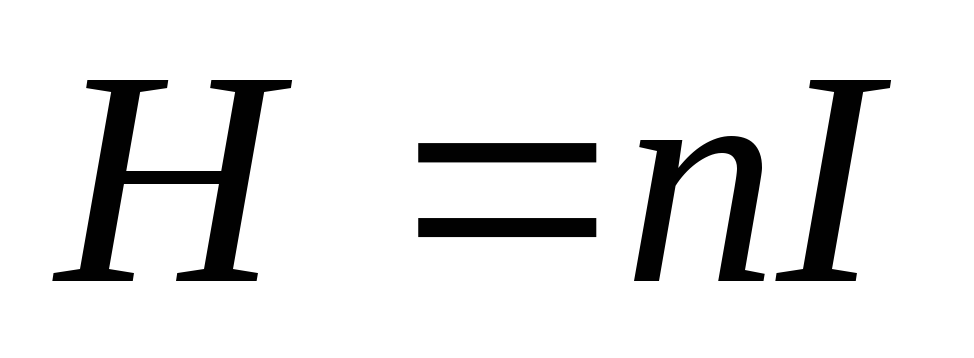 .
Энергия единицы объема (т.е.плотность
энергии магнитного поля,
.
Энергия единицы объема (т.е.плотность
энергии магнитного поля,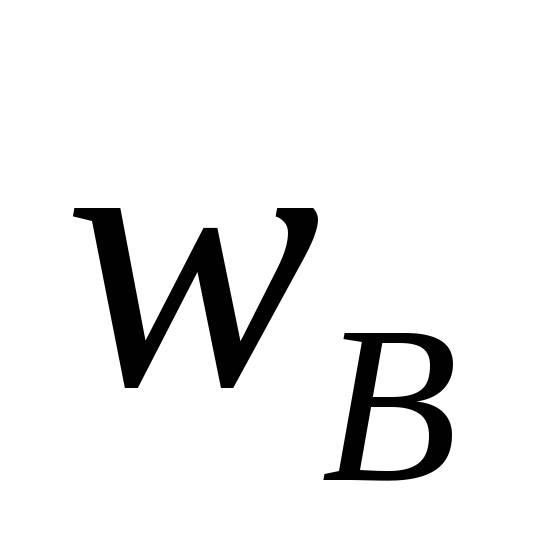 )
равна
)
равна
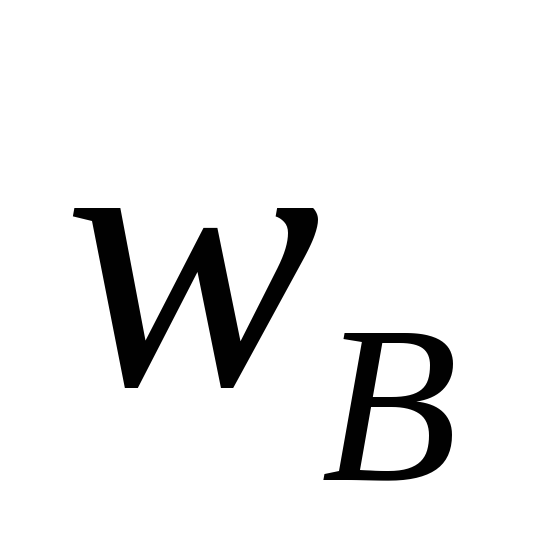 =
=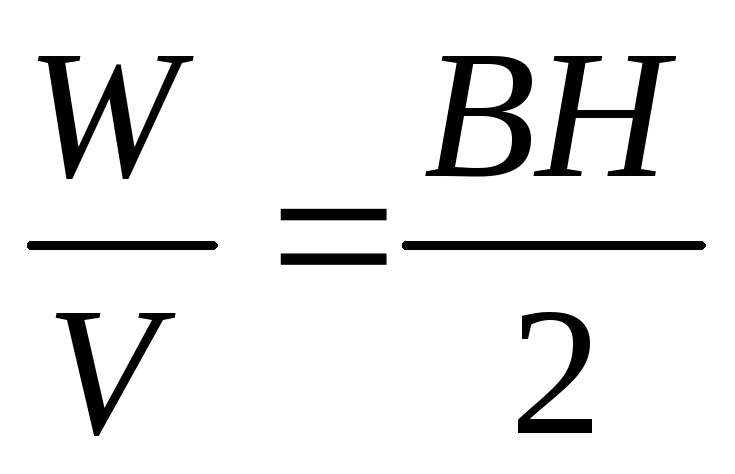 . (108)
. (108)
Для неоднородного магнитного поля
плотность энергии  ,
кроме того, расчет показывает, что
выражение (108) верно и в векторном виде:
,
кроме того, расчет показывает, что
выражение (108) верно и в векторном виде:
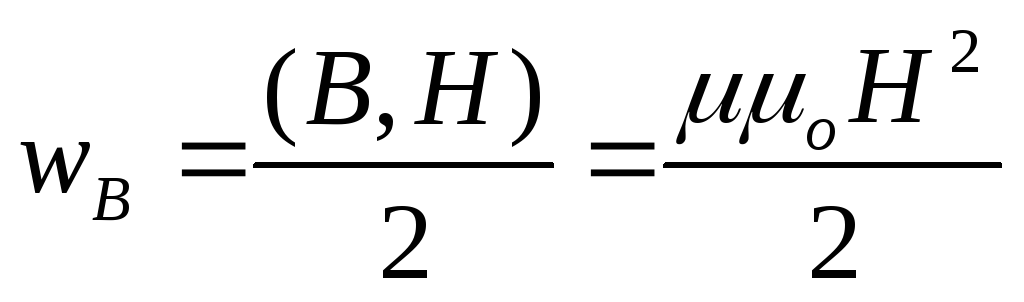 . (109)
. (109)
studfile.net
Электромагнитная индукция — урок. Физика, 9 класс.
Индукционный ток
Великому английскому физику Майклу Фарадею потребовалось почти \(10\) лет, чтобы ответить в \(1831\) году на вопрос, как «превратить магнетизм в электричество».
Что же служит причиной появления тока в катушке, в цепи которой нет источника тока? Ток в катушке всегда возникает при изменении магнитного поля, в котором она находится.
Электрический ток в замкнутом контуре, возникающий при изменении магнитного поля, называется индукционным.
Индукционный ток, так же как и ток от гальванического элемента или аккумулятора, представляет собой упорядоченное движение электронов.
Причины электромагнитной индукции
Явление возникновения индукционного тока в контуре называют электромагнитной индукцией.
Многочисленные опыты М. Фарадея привели к выводу, что индукционный ток в контуре, замкнутом на гальванометр, возникает при изменении:
- магнитного поля;

- площади контура;

- ориентации контура в магнитном поле.

Во всех случаях изменяется число линий магнитной индукции, то есть меняется магнитный поток.
Индукционный ток возникает при всяких изменениях магнитного потока Ф, пронизывающего контур замкнутого проводника.
Если же магнитный поток через поверхность, ограниченную контуром, не меняется, то индукционный ток в контуре не возникает.
Пример:
если вращать полосовой магнит внутри катушки, замкнутой на гальванометр, вокруг его вертикальной оси, то индукционный ток не возникает, так как магнитный поток не меняется.

Развитие электротехники
Открытие электромагнитной индукции вызвало появление и бурное развитие электротехники. На основе этого явления были созданы генераторы электрической энергии. В их разработке принимали участие учёные и техники разных стран, в том числе и наши соотечественники: Э. Х. Ленц, Б. С. Якоби, М. И. Доливо-Добровольский и др.
Применение электромагнитной индукции
Явление электромагнитной индукции лежит в основе действия индукционной плиты. Индукционные токи при изменении магнитного поля возникают не только в проволочных контурах, но и в массивных образцах металла. Эти токи называют вихревыми токами, или токами Фуко. В массивных проводниках вследствие малости электрического сопротивления токи могут быть очень большими и вызывать значительное нагревание. Принцип работы индукционной плиты показан на рисунке. Под стеклокерамической поверхностью плиты находится катушка индуктивности, по которой протекает переменный электрический ток, создающий переменное магнитное поле. Частота тока составляет \(20\)–\(60\) кГц. В дне посуды наводятся токи индукции, которые нагревают его, а заодно и помещённые в посуду продукты. Нет никакой теплопередачи снизу вверх, от конфорки через стекло к посуде, а значит, нет и тепловых потерь. С точки зрения эффективности использования потребляемой электроэнергии индукционная плита выгодно отличается от всех других типов кухонных плит.

1 — посуда из ферромагнитного материала;
2 — стеклокерамическая поверхность;
3 — слой изоляции;
4 — катушка индуктивности.
www.yaklass.ru


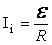 . e не зависит от свойств контура:
. e не зависит от свойств контура: 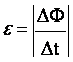 .
.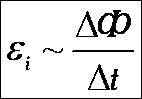
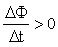 ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю:
; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: 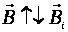 , где
, где 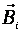 — т.н. индукционное магнитное поле.
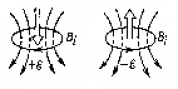
— т.н. индукционное магнитное поле.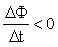 . Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем:
. Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем: 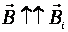 .
.
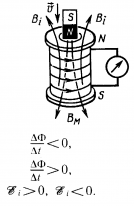
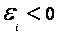 ),если
),если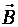 (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (
(т.е. ΔΦ>0). Ток в контуре имеет положительное направление (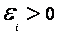 ), если
), если 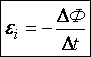 .
.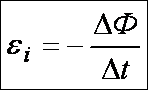
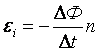 ,
,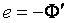 , где e – мгновенное значение ЭДС индукции.
, где e – мгновенное значение ЭДС индукции.