Индуктивность катушки при увеличении частоты переменного тока

Как изменится индуктивное сопротивление катушки при уменьшении частоты переменного тока в 4 раза?

2) увеличится в 4 раза

3) уменьшится в 2 раза

4) уменьшится в 4 раза

Индуктивное сопротивление катушки пропорционально циклической частоты текущего через нее переменного тока: Следовательно, уменьшение частоты переменного тока в 4 раза приведет к уменьшению индуктивного сопротивления также в 4 раза.

Катушка индуктивности (inductor. -eng)– устройство, основным компонентом которого является проводник скрученный в кольца или обвивающий сердечник. При прохождении тока, вокруг скрученного проводника (катушки), образуется магнитное поле (она может концентрировать переменное магнитное поле), что и используется в радио- и электро- технике.

К точной и компьютерной технике технике больше близок дроссель (Drossel, регулятор, ограничитель), так как он чаще всего применяется в цепях питания процессоров, видеокарт, материнских плат, блоков питания & etc.

В последнее время, применяются индукторы закрытые в корпуса из металлического сплава для уменьшения наводок, излучения, шумов и высокочастотного свиста при работе катушки.

Дроссель служит для уменьшения пульсаций напряжения, сглаживания или фильтрации частотной составляющей тока и устранения переменной составляющей тока. Сопротивление дросселя увеличивается с увеличением частоты, а для постоянного тока сопротивление очень мало. Характеристики дросселя получаются от толщины проводника, количества витков, сопротивления проводника, наличия или отсутствия сердечника и материала, из которого сердечник сделан. Особенно эффективными считаются дроссели с ферритовыми сердечниками (а также из альсифера, карбонильного железа, магнетита) с большой магнитной проницаемостью.

Используется в выпрямителях, сетевых фильтрах, радиотехнике, питающих фазах высокоточной аппаратуры и другой технике требующей стабильного и «правильного» питания. Многослойная катушка может выступать и в качестве простейшего конденсатора, так как имеет собственную ёмкость. Правда, от данного эффекта пытаются больше избавиться, чем его усиливать и он считается паразитным.

Как работает дроссель.

В цепях переменного тока, для ограничения тока нагрузки, очень часто применяют дроссели — индуктивные сопротивления. Перед обычными резисторами здесь у дросселей имеется серьезные преимущества — значительная экономия электроэнергии и отсутствие сильного нагрева.

Каково устройство дросселя, на чем основан принцип его работы?

Устроен дроссель очень просто — это катушка из электрического провода, намотанная на сердечнике из ферромагнитного материала. Приставка ферро, говорит о присутствии железа в его составе (феррум — латинское название железа), в том или ином количестве.

Принцип работы дросселя основан на свойстве, присущем не только катушкам но и вообще, любым проводникам — индуктивности. Это явление легче всего понять, поставив несложный опыт.

Для этого требуется собрать простейшую электрическую цепь, состоящую из низковольтного источника постоянного тока (батарейки), маленькой лампочки накаливания, на соответствующее напряжение и достаточно мощного дросселя (можно взять дроссель от лампы ДРЛ-400 ватт).

Без дросселя, схема будет работать как обычно — цепь замыкается, лампа загорается. Но если добавить дроссель, подключив его последовательно нагрузке(лампочке), картина несколько изменится.

Присмотревшись, можно заметить, что во первых, лампа загорается не сразу, а с некоторой задержкой, во вторых — при размыкании цепи возникает хорошо заметная искра, прежде не наблюдавшаяся. Так происходит потому что, в момент включения ток в цепи возрастает не сразу — этому препятствует дроссель, некоторое время поглощая электроэнергию и запасая ее в виде электромагнитного поля. Эту способность и называют — индуктивностью.

Чем больше величина индуктивности, тем большее количество энергии может запасти дроссель. Еденица величины индуктивности — 1 Генри В момент разрыва цепи запасеная энергия освобождается, причем напряжение при этом может превысить Э.Д.С. используемого источника в десятки раз, а ток направлен в противоположную сторону. Отсюда заметное искрение в месте разрыва.

Это явление называется — Э.Д.С. самоиндукции.

Если установить источник переменного тока вместо постоянного, использовав например, понижающий трансформатор, можно обнаружить что та же лампочка, подключенная через дроссель — не горит вовсе. Дроссель оказывает переменному току гораздо большое сопротивление, нежели постояному. Это происходит из за того, что ток в полупериоде, отстает от напряжения.

Получается, что действующее напряжение на нагрузке падает во много раз(и ток соответственно), но энергия при этом не теряется — возвращается за счет самоиндукции обратно в цепь. Сопротивление оказываемое индуктивностью переменному току называется — реактивным. Его значение зависит от величины индуктивности и частоты переменного тока. Величина индуктивности в свою очередь, находится в зависимости от количества витков катушки и свойства материала сердечника, называемого — магнитной проницаемостью, а так же его формы.

Магнитная проницаемость — число, показывающее во сколько раз индуктивность катушки больше с сердечником из данного материала, нежели без него(в идеале — в вакууме. )

Т. е — магнитная проницаемость вакуума принята за еденицу.

В радиочастотных катушках малой индуктивности, для точной подстройки применяются сердечники стержеобразной формы. Материалами для них могут являться ферриты с относительно небольшой магнитной проницаемостью, иногда немагнитные материалы с проницаемостью меньше 1.

В электромагнитах реле — сердечники подковоообразной и цилиндрической формы из специальных сталей.

Для намотки дросселей и трансформаторов используют замкнутые сердечники — магнитопроводы Ш — образной и тороидальной формы. Материалом на частотах до 1000 гц служит специальная сталь, выше 1000 гц — различные ферросплавы. Магнитопроводы набираются из отдельных пластин, покрытых лаком.

У катушки, намотанной на сердечник, кроме реактивного(Xl) имеется и активное сопротивление(R). Таким образом, полное сопротивление катушки индуктивности равно сумме активной и реактивной составляющих.

Как работает трансформатор.

Рассмотрим работу дросселя собранного на замкнутом магнитопроводе и подключенного в виде нагрузки, к источнику переменного тока. Число витков и магнитная проницаемость сердечника подобраны таким образом, что его реактивное сопротивление велико, ток протекающий в цепи соответственно — нет.

Ток, переодически изменяя свое направление, будет возбуждать в обмотке катушки (назовем ее катушка номер 1) электромагнитное поле, направление которого будет также переодически меняться — перемагничивая сердечник. Если на этот же сердечник поместить дополнительную катушку(назовем ее — номер 2), то под действием переменного электромагнитного поля сердечника, в ней возникнет наведенная переменная Э.Д.С.

Если количество витков обеих катушек совпадает, то значение наведенной Э.Д.С. очень близко к значению напряжения источника питания, поданного на катушку номер 1. Если уменьшить количество витков катушки номер 2 вдвое, то значение наведенной Э.Д.С. уменьшится вдвое, если количество витков наоборот, увеличить — наведенная Э.Д.С. также, возрастет. Получается, что на каждый виток, приходится какая-то определенная часть напряжения.

Обмотку катушки на которую подается напряжение питания (номер 1) называют первичной. а обмотка, с которой трансформированое напряжение снимается — вторичной .

Отношение числа витков вторичной(Np ) и первичной (Ns ) обмоток равно отношению соответствующих им напряжений — Up (напряжение первичной обмотки) и Us (напряжение вторичной обмотки).

Таким образом, устройство состоящее из замкнутого магнитопровода и двух обмоток в цепи переменного тока можно использовать для изменения питающего напряжения — трансформации. Соответственно, оно так и называется — трансформатор .

Если подключить к вторичной обмотке какую-либо нагрузку, в ней возникнет ток(Is ). Это вызовет пропорциональное увеличение тока(Ip ) и в первичной обмотке. Будет верным соотношение:

Трансформаторы могут применяться как для преобразовния питающего напряжения, так и для развязки и согласования усилительных каскадов. При работе с трансформаторами необходимо обратить внимание на ряд важных параметров, таких как:

1. Допустимые токи и напряжения для первичной и вторичной обмоток.

2. Максимальную мощность трансформатора — мощность которая может длительное время передаваться через него, не вызывая перегрева обмоток.

3. Диапазон рабочих частот трансформатора.

Параллельный колебательный контур.

Если соединить катушку индуктивности и конденсатор — получится очень интересный элемент радиотехники — колебательный контур. Если зарядить конденсатор или навести в катушке Э.Д.С. используя электромагнитное поле — в контуре начнут происходить следующие процессы: Конденсатор разряжаясь, возбуждает электромагнитное поле в катушке индуктивности. Когда заряд истощается, катушка индуктивности возвращает запасенную энергию обратно в конденсатор, но уже с противоположным знаком, за счет Э.Д.С. самоиндукции. Это будет повторяться снова и снова — в контуре возникнут электромагнитные колебания синусоидальной формы. Частота этих колебаний называется резонансной частотой контура, и зависит от величин емкости конденсатора(С), и индуктивности катушки (L).

Параллельный колебательный контур обладает очень большим сопротивлением на своей резонансной частоте. Это позволяет использовать его для частотной селекции(выделения) в входных цепях радиоаппаратуры и усилителях промежуточной частоты, а так же — в различных схемах задающих генераторов.

Цветовая и кодовая маркировка индуктивностей.

Обычно для индуктивностей кодируется номинальное значение индуктивности и допуск, т.е. допускаемое отклонение от указанного номинала. Номинальное значение кодируется цифрами, а допуск — буквами. Применяется два вида кодирования.

Первые две цифры указывают значение в микрогенри (мкГн), последняя — количество нулей. Следующая за цифрами буква указывает на допуск. Например, код 101J обозначает 100 мкГн ±5%. Если последняя буква не указывается —допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.

D=±0,3 нГн; J=±5%; К=±10%; M=±20%

Индуктивности маркируются непосредственно в микрогенри (мкГн). В таких случаях маркировка 680К будет означать не 68 мкГн ±10%, как в случае А, а 680 мкГн ±10%.

Как измерить индуктивность катушки, дросселя.

ЗЫ: Взял где взял, обобщил и добавил немного.

Простите за качество некоторых картинок (чем богаты).

Берегите себя и своих близких!

Дубликаты не найдены

Как измерить индуктивность катушки мультиметром? Взять мультиметр с функцией измерения индуктивности. Лодку мне.

Рассмотрим цепь, содержащую в себе катушку индуктивности , и предположим, что активное сопротивление цепи, включая провод катушки, настолько мало, что им можно пренебречь. В этом случае подключение катушки к источнику постоянного тока вызвало бы его короткое замыкание, при котором, как известно, сила тока в цепи оказалась бы очень большой.

Иначе обстоит дело, когда катушка присоединена к источнику переменного тока. Короткого замыкания в этом случае не происходит. Это говорит о том. что катушка индуктивности оказывает сопротивление проходящему по ней переменному току .

Каков характер этого сопротивления и чем оно обусловливается?

Чтобы ответить ил этот вопрос, вспомним явление самоиндукции. Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости изменения тока в ней. Но так как переменный ток непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току.

Для уяснения процессов, происходящих в цепи переменного тока с катушкой индуктивности, обратимся к графику. На рисунке 1 построены кривые линии, характеризующие соответственно тик в цепи, напряжение на катушке и возникающую в ней ЭДС самоиндукции. Убедимся в правильности произведенных па рисунке построений.

Цепь переменного тока с катушкой индуктивности

С момента t = 0, т. е. с начального момента наблюдения за током, он начал быстро возрастать, но по мере приближения к своему максимальному значению скорость нарастания тока уменьшалась.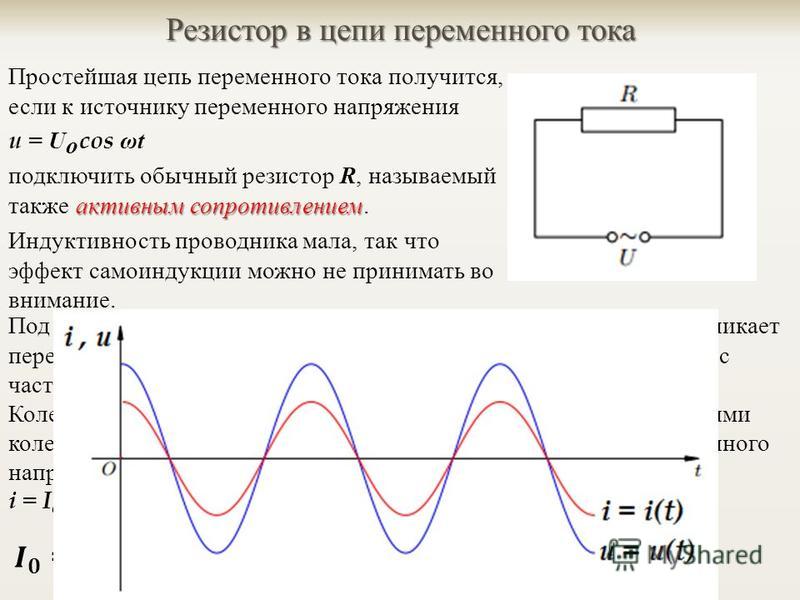 В момент, когда ток достиг максимальной величины, скорость его изменения на мгновение стала равной нулю, т. е. прекратилось изменение тока. Затем ток начал сначала медленно, а потом быстро убывать и по истечении второй четверти периода уменьшился до нуля. Скорость же изменения тока за эту четверть периода, возрастая от пуля, достигла наибольшей величины тогда, когда ток станет равным нулю.

Рисунок 2. Характер изменений тока во времени в зависимости от величины тока

Из построений на рисунке 2 видно, что при переходе кривой тока через ось времени увеличение тока за небольшой отрезок времени t больше, чем за этот же отрезок времени, когда кривая тока достигает своей вершины.

Следовательно, скорость изменения тока уменьшается по мере увеличения тока и увеличивается по мере его уменьшения, независимо от направления тока в цепи.

Очевидно, и ЭДС самоиндукции в катушке должна быть наибольшей тогда, когда скорость изменения тока наибольшая, и уменьшаться до нуля, когда прекращается его изменение. Действительно, на графике кривая ЭДС самоиндукции e _L за первую четверть периода, начиная от максимального значения, упала до нуля (см. рис. 1).

На протяжении следующей четверти периода ток от максимального значения уменьшался до нуля, однако скорость его изменения постепенно возрастала и была наибольшей в момент, когда ток стал равным нулю. Соответственно и ЭДС самоиндукции за время этой четверти периода, появившись вновь в катушке, постепенно возрастала и оказалась максимальной к моменту, когда ток стал равным нулю.

Однако направление свое ЭДС самоиндукции изменила на обратное, так как возрастание тока в первой четверти периода сменилось во второй четверти его убыванием.

Цепь с индуктивностью

Продолжив дальше построение кривой ЭДС самоиндукции, мы убеждаемся в том, что за период изменения тока в катушке и ЭДС самоиндукции совершит в ней полный период своего изменения. Направление ее определяется законом Ленца: при возрастании тока ЭДС самоиндукции будет направлена против тока (первая и третья четверти периода), а при убывании тока, наоборот, совпадать с ним по направлению (вторая и четвертая четверти периода).

Таким образом, ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и , наоборот, поддерживает его при убывании .

Обратимся теперь к графику напряжения на катушке (см. рис. 1). На этом графике синусоида напряжения на зажимах катушки изображена равной и противоположной синусоиде ЭДС самоиндукции. Следовательно, напряжение на зажимах катушки в любой момент времени равно и противоположно ЭДС самоиндукции, возникающей в ней. Напряжение это создается генератором переменного тока и идет на то, чтобы погасить действие в цепи ЭДС самоиндукции.

Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки , то и называется оно индуктивным сопротивлением.

Индуктивное сопротивление обозначается через X _L и измеряется, как и активное сопротивление, в омах.

Индуктивное сопротивление цепи тем больше, чем больше частота источника тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле X L = ω L , где ω — круговая частота, определяемая произведением 2π f . — индуктивность цепи в гн.

Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна индуктивному сопротивлению це п и , т. е. I = U / X _L , где I и U — действующие значения тока и напряжения, а X _L — индуктивное сопротивление цепи.

Рассматривая графики изменения тока в катушке. ЭДС самоиндукции и напряжения на ее зажимах, мы обратили внимание на то, что изменение этих в еличин не совпадает по времени. Иначе говоря, синусоиды тока, напряжения и ЭДС самоиндукции оказались для рассматриваемой нами цепи сдвинутыми по времени одна относительно другой. В технике переменных токов такое явление принято называть сдвигом фаз .

Если же две переменные величины изменяются по одному и тому же закону (в нашем случае по синусоидальному) с одинаковыми периодами, одновременно достигают своего максимального значения как в прямом, так и в обратном направлении, а также одновременно уменьшаются до нуля, то такие переменные величины имеют одинаковые фазы или, как говорят, совпадают по фазе.

В качестве примера на рисунке 3 приведены совпадающие по фазе кривые изменения тока и напряжения. Такое совпадение фаз мы всегда наблюдаем в цепи переменного тока, состоящей только из активного сопротивления.

В том случае, когда цепь содержит индуктивное сопротивление, фазы тока и напряжения, как это видно из рис. 1 не совпадают, т. е. имеется сдвиг фаз между этими переменными величинами. Кривая тока в этом случае как бы отстает от кривой напряжения на четверть периода.

Следовательно, при включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между током и напряжением, причем ток отстает по фазе от напряжения на четверть периода . Это значит, что максимум тока наступает через четверть периода после того, как наступил максимум напряжения.

ЭДС же самоиндукции находится в противофазе с напряжением на катушке, отставая, в свою очередь, от тока на четверть периода. При этом период изменения тока, напряжения, а также и ЭДС самоиндукции не меняется и остается равным периоду изменения напряжения генератора, питающего цепь. Сохраняется также и синусоидальный характер изменения этих величин.

Рисунок 3. Совпадение по фазе тока и напряжения в цепи с активным сопротивлением

Выясним теперь, каково отличие нагрузки генератора переменного тока активным сопротивлением от нагрузки его индуктивным сопротивлением.

Когда цепь переменного тока содержит в себе лишь одно активное сопротивление, то энергия источника тока поглощается в активном сопротивлении, нагревая проводник.

Когда же цепь не содержит активного сопротивления (мы условно считаем его равным нулю), а состоит лишь из индуктивного сопротивления катушки, энергия источника тока расходуется не на нагрев проводов, а только на создание ЭДС самоиндукции, т. е. она превращается в энергию магнитного поля. Однако переменный ток непрерывно изменяется как по величине, так и по направлению, а следовательно, и магнитное поле катушки непрерывно изменяется в такт с изменением тока. В первую четверть периода, когда ток возрастает, цепь получает энергию от источника тока и запасает ее в магнитном поле катушки. Но как только ток, достигнув своего максимума, начинает убывать, он поддерживается за счет энергии, запасенной в магнитном поле катушки посредством ЭДС самоиндукции.

Таким образом, источник тока, отдав в течение первой четверти периода часть своей энергии в цепь, в течение второй четверти получает ее обратно от катушки, выполняющей при этом роль своеобразного источника тока. Иначе говоря, цепь переменного тока, содержащая только индуктивное сопротивление, не потребляет энергии : в данном случае происходит колебание энергии между источником и цепью. Активное же сопротивление, наоборот, поглощает в себе всю энергию, сообщенную ему источником тока.

Говорят, что катушка индуктивности, в противоположность омическому сопротивлению, не активна по отношению к источнику переменного тока, т. е. реактивна . Поэтому индуктивное сопротивление катушки называют также реактивным сопротивлением .

Катушка индуктивности

 

3.5. Катушки индуктивности

 

1. Общие сведения. Характеристики

Вам известно, что проводник, намотанный на сердечник в виде катушки, в цепях переменного тока обладает индуктивным сопротивлением, которое зависит от частоты тока и геометрических характеристик проводника. Индуктивность выражает свойство проводника препятствовать изменению тока в нем, она характеризует количество энергии, запасенное проводником при протекании по нему электрического тока. Индуктивность зависит от формы, размеров, числа витков катушки и материала ее сердечника.

По конструкции выделяют цилиндрические, плоские (спиральные) и тороидальные катушки. Они могут быть одно- и многослойными, с сердечниками и без них, экранированными и нет.

Реальная катушка, кроме индуктивного сопротивления, всегда обладает активным сопротивлением, которое иногда называется сопротивлением потерь. Поэтому используют схему замещения катушки, чаще всего последовательную (рис. 3.19). Качество катушек характеризуют добротностью — отношением ее реактивного сопротивления к активному сопротивлению потерь.

Температурный коэффициент индуктивности равен относительному изменению индуктивности при изменении температуры окружающей среды на 1⁰ С.

Паразитным параметром, обуславливающим увеличение потерь энергии в катушке, является ее собственная емкость.

2. Измерение индуктивности

Одним из методов измерения индуктивности является метод вольтметра-амперметра. При его использовании необходимо выполнение условия: активное сопротивление катушки R_L должно быть

 значительно меньше ее индуктивного сопротивления X_L­. Тогда из закона Ома     , откуда

Как и в случае измерения активных сопротивлений, в зависимости от значения индуктивного сопротивления катушки можно пользоваться схемой, изображенной на рисунке 3.20а (при малых индуктивных сопротивлениях, то есть малых индуктивностях), или схемой, изображенной на рисунке 3.20б (при больших индуктивных сопротивлениях, то есть больших индуктивностях).

Для уменьшения погрешности измерения необходимо также учитывать активное сопротивление катушки, так как ее полное сопротивление , отсюда

С увеличением частоты подаваемого напряжения точность измерений уменьшается из-за влияния собственной емкости катушки и входной емкости вольтметра, которые суммируются. Емкость и измеряемая индуктивность образуют параллельный контур, сопротивление которого при резонансе возрастает, что эквивалентно увеличению индуктивности. Поэтому значение индуктивности, полученное в результате измерения, будет больше действительного значения, причем погрешность увеличивается при увеличении частоты напряжения питания.

Достаточно часто применяется мостовой метод измерения индуктивности. В качестве плеча сравнения может использоваться образцовая катушка индуктивности или образцовый конденсатор — C₂ (рис. 3.21). Конденсатор применяется чаще в связи с трудностями изготовления катушек с малыми потерями. Условие равновесия моста

Z_x Z₂ = Z Z₁, где Z_i = R_i + j X_i, запишется в виде:          

Разделив вещественную и мнимую части, получим выражения для индуктивности катушки и ее активного сопротивления: L_х=C₂RR₁, R_x=RR₁/R₂.

Добротность катушки определяется выражением  Q_x=wL_x/R_x=wR₂C₂.

Уравновешивание моста достигается плавной регулировкой параметров R₂ и C₂. Изменяя произведение RR₁, можно расширить пределы измерения моста.

 

 

Катушка индуктивности в цепи постоянного и переменного тока

Как ведет себя катушка индуктивности в цепи постоянного и переменного тока?

Катушка индуктивности в цепи постоянного тока

Итак, для этого опыта нам понадобится блок питания, который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.

Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:

Намотать на него лакированного медного провода и зачистить выводы:

Замеряем индуктивность нашей катушки с помощью LC метра:

132 микрогенри.

Теперь собираем все это вот по такой схеме:

где

L – катушка индуктивности

La – лампочка накаливания на напряжение 12 Вольт

Bat – блок питания, с выставленным напряжением 12 Вольт

Лампочка засветилась!

Как вы помните из прошлой статьи, конденсатор у нас не пропускал  постоянный электрический ток:

Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам  провод, из которого намотана катушка.

[quads id=1]

Катушка индуктивности в цепи переменного тока

Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом.  Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него

Собираем все это дело по такой схеме:

Получилось как то так:

Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал – желтым. Следовательно, красная синусоида – это частота, которую нам выдает генератор частоты, а желтая синусоида – это сигнал, который снимается с резистора.

Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.

Опыт N1

Для начала подаем сигнал  с частотой  в 1 Килогерц.

Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф

Красный кружок с цифрой “1” – это замеры “красного”канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой “2”. F=1 Килогерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.

Увеличиваем частоту до 10 Килогерц

Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.

Увеличиваем до 100 Килогерц

Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.

Сдвиг фаз – это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Увеличиваем частоту до 200 Килогерц

На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.

Увеличиваем частоту до 300 Килогерц.

Амплитуда  желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.

Увеличиваем частоту до 500 Килогерц

Амплитуда уменьшилась до 480 милливольт.

Добавляем еще частоту до 1 Мегагерц

Амплитуда желтого канала  стала 280 милливольт.

Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца

Амплитуда “желтого” сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.

И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.

[quads id=1]

Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:

Так какой вывод можно сделать?

С увеличением частоты сопротивление катушки растет,  а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.

Опыт N2

Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.

Итак, прогоняем все по тем же значениям частоты

При  частоте в 1 Килогерц у  нас значение почти не изменилось.

10 Килогерц

Здесь тоже  ничего не изменилось.

100 Килогерц

Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.

200 Килогерц

Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.

300 Килогерц

Сдвиг фаз стал больше и амплитуда просела еще больше

500 Килогерц

Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.

1 Мегагерц

Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉

2 Мегагерца, предел моего генератор частоты

Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.

Обратите внимание на амплитуду в Вольтах  на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.

Отсюда вывод напрашивается сам собой:

При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.

Реактивное сопротивление катушки индуктивности

С помощью нехитрых умозаключений, физиками была выведена формула:

где

Х_L –  реактивное сопротивление катушки, Ом

П – постоянная и равна  приблизительно 3,14

F – частота, Гц

L – индуктивность, Гн

В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда  и мощность  на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.

Видео про катушку индуктивности:

Заключение

Постоянный ток протекает через катушку индуктивности без каких-либо проблем. Сопротивлением обладает только сам провод, из которого намотана катушка.

Сопротивление катушки зависит от частоты протекающего через нее тока и выражается формулой:

Катушка индуктивности в цепи переменного тока

Принцип работы

Чтобы понять принцип действия катушки индукции, следует знать:

• вокруг движущихся электрически заряженных частиц (электрический ток) возникает электромагнитное поле. Если проводник с протекающим током смотан в катушку, поле многократно усиливается. Еще большим оно становится при использовании металлического сердечника, что объясняется высокой магнитопроницаемостью металлов по сравнению с воздухом;
• переменное магнитное поле наводит в проводнике ЭДС (закон электромагнитной индукции, открытый М. Фарадеем).

Способность катушки превращать электрическую энергию в магнитное поле, называется индуктивностью. Она измеряется в генри (Гн), в формулах обозначается литерой L. Катушка индуктивностью в 1 Гн при изменении силы тока со скоростью dI = 1 А/с (ампер в секунду) создает ЭДС в 1 В. Индуктивность катушки зависит от ее длины, потому шаг витков стремятся делать как можно меньшим.

Сердечник в катушке может быть регулируемым, тогда элемент имеет переменную индуктивность. Также применяют катушки вовсе без сердечника. Если катушка включена в цепь постоянного тока, то весь эффект от нее состоит в создании электромагнитного поля. Так устроены, например, электрические магниты для захвата металлолома, устанавливаемые на погрузочных кранах.

При проведении эксперимента надо ограничить ток в цепи, посредством включенной последовательно с катушкой нагрузки, иначе возникнет короткое замыкание.

Мощность в индукторе

Мы знаем, что индуктор в цепи противостоит потоку тока I через него, потому что поток этого тока индуцирует ЭДС, которая противостоит ему, закон Ленца. Затем необходимо выполнить работу от внешнего источника батареи, чтобы ток протекал против этой индуцированной ЭДС. Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V _L), определяется как:

Мощность в цепи задается как P = V * I, поэтому:

Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и поэтому мощность в катушке не рассеивается, поэтому можно сказать, что идеальный индуктор имеет нулевую потерю мощности.

Обзор пассивных компонентов

Современная радиоэлектронная аппаратура (РЭА) содержит огромное количество электрорадиокомпонентов, т.е. самостоятельных  изделий, выполняющих определенные функции. Электрорадиоэлементы подразделяют на активные и пассивные. К активным относятся транзисторы,  микросхемы ,электронные лампы и т.д., т. е. элементы, способные усиливать или преобразовывать электрические сигналы. К пассивным относятся резисторы, катушки индуктивности, конденсаторы, трансформаторы, коммутационные элементы, т. е. такие элементы, которые предназначены для перераспределения электрической энергии.

Сетевая инфраструктура современного офиса состоит из множества составляющих, правильный выбор которых имеет существенное значение для успешной работы всей инфраструктуры в целом. Пассивные компоненты  играют при этом также немаловажную  роль, обеспечивают среде передачу данных, а также внешний вид, эстетику. Пассивным элементом схемы называется элемент, не имеющий внутренних источников энергии, и выполняющий либо накопление энергии (конденсатор, индуктивность), либо ее рассеяние (резистор).

Пассивные компоненты по сути соответствует пассивному элементу схемы. Пассивные компоненты характеризуются малыми размерами, малым числом выводов (как правило, два-три), низкой стоимостью и, как правило, достаточно высокой стойкостью к воздействиям при сборке узлов. Пассивные элементы могут выступать как дискретные компоненты и как элементы интегральных микросхем. В РЭА интегральные микросхемы  имеют очень большой удельный вес, но пассивные компоненты являются все же самыми распространенными изделиями электронной промышленности. Это можно объяснить  тем, что некоторые элементы трудно выполнить в микросхемном исполнении. Практически невозможно в ИМС изготовить конденсаторы большой емкости, резисторы с большим сопротивлением, сложности в разработке интегральных катушек индуктивности и трансформаторов. Кроме того технические характеристики дискретных элементов лучше, чем интегральных.

Катушки индуктивности разных размеров

Предыдущая
РадиодеталиЧто такое подстроечный резистор: описание устройства и область его применения
Следующая
РадиодеталиДроссели в электрике: что это и где используются?

Назначение и принцип действия

Специалисты задаются вопросом, зачем нужна токовая катушка индуктивности в цепи, и для этого необходимо разобраться в показателях. Коэффициент ЭДС (электродвижущая сила) показывает разницу между энергией и магнитным потоком. Устройства самоиндукции способны влиять на изменения в цепи. Чаще всего дроссели применяются в силовых установках. Они способны контролировать уровень напряжения, не допускают разрыва цепи.

Устройства самоиндукции

Также компоненты устанавливаются на пару с конденсаторами либо резисторами. Благодаря работе катушки фильтры находятся в безопасности. Теперь вызывает интерес, как включается индукционная катушка. Принцип работы построен на изоляции проводников. В конструкции используется электрический каркас с различным сечением. За счёт намоток обеспечивается распределение ёмкости на дросселе.

Интересно! Витки наматываются с определенным шагом, многое зависит от типа катушки.

Свойства катушки индуктивности

Свойства катушки индуктивности:

• Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
• Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
• Катушка индуктивности при протекании тока запасает энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.

Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое (активное) сопротивление, но и реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

Катушка индуктивности обладает реактивным сопротивлением, модуль которого XL=ωL{\displaystyle X_{L}=\omega L}, где L{\displaystyle L} — индуктивность катушки, ω{\displaystyle \omega } — циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.

Катушка с током запасает энергию в магнитном поле, равную работе, которую необходимо совершить для установления текущего тока I{\displaystyle I}.{2}{\mbox{.}}}

При изменении тока в катушке возникает ЭДС самоиндукции, значение которой:

ε=−LdIdt.{\displaystyle \varepsilon =-L{dI \over dt}{\mbox{.}}}

Для идеальной катушки индуктивности (не имеющей паразитных параметров) ЭДС самоиндукции равна по модулю и противоположна по знаку напряжению на концах катушки:

|ε|=−ε=U.{\displaystyle |\varepsilon |=-\varepsilon =U{\mbox{.}}}

При замыкании катушки с током на резистор происходит переходной процесс, при котором ток в цепи экспоненциально уменьшается в соответствии с формулой:

I=Iexp(−tT),{\displaystyle I=I_{0}exp(-t/T){\mbox{,}}}

где : I{\displaystyle I} — ток в катушке,

I{\displaystyle I_{0}} — начальный ток катушки,

t{\displaystyle t} — текущее время,

T{\displaystyle T} — постоянная времени.

Постоянная времени выражается формулой:

T=L(R+Ri),{\displaystyle T=L/(R+R_{i}){\mbox{,}}}

где R{\displaystyle R} — сопротивление резистора,

Ri{\displaystyle R_{i}} — омическое сопротивление катушки.

При закорачивании катушки с током процесс характеризуется собственной постоянной времени Ti{\displaystyle T_{i}} катушки:

Ti=LRi.{\displaystyle T_{i}=L/R_{i}{\mbox{.}}}

При стремлении Ri{\displaystyle R_{i}} к нулю, постоянная времени стремится к бесконечности, именно поэтому в сверхпроводящих контурах ток течёт «вечно».

В цепи синусоидального тока, ток в катушке по фазе отстаёт от фазы напряжения на ней на π/2.

Явление самоиндукции аналогично проявлению инертности тел в механике, если аналогом индуктивности принять массу, тока — скорость, напряжения — силу, то многие формулы механики и поведения индуктивности в цепи принимают похожий вид:

F =mdvdt{\displaystyle F\ =m{dv \over dt}} |ε|=LdIdt{\displaystyle |\varepsilon |=L{dI \over dt}},

где

F {\displaystyle F\ } |ε|{\displaystyle |\varepsilon |} U {\displaystyle U\ } ; m {\displaystyle m\ } L {\displaystyle L\ } ; dv {\displaystyle dv\ } dI {\displaystyle dI\ }

Ecoxp=12LI2{\displaystyle E_{\mathrm {coxp} }={1 \over 2}LI^{2}} Ekinet=12mv2{\displaystyle E_{\mathrm {kinet} }={1 \over 2}mv^{2}}

Ток и напряжение в индукторе

Сколько индуктивного напряжения будет генерироваться индуктором, зависит от скорости изменения тока. В нашем уроке об электромагнитной индукции закон Ленца гласил: «Направление индуцированной ЭДС таково, что оно всегда будет противостоять изменению, которое его вызывает». Другими словами, индуцированная ЭДС всегда будет противопоставлять движение или изменение, которые изначально вызвали индуцированную ЭДС.

Таким образом, при уменьшении тока полярность напряжения будет действовать как источник, а при увеличении тока полярность напряжения будет действовать как нагрузка. Таким образом, при одинаковой скорости изменения тока через катушку, увеличение или уменьшение величины индуцированной ЭДС будет одинаковым.

Конструкция

Конструктивно выполняется в виде винтовых или винтоспиральных (диаметр намотки изменяется по длине катушки) катушек однослойных или многослойных намоток изолированного одножильного или многожильного (литцендрат) проводника на диэлектрическом каркасе круглого, прямоугольного или квадратного сечения, часто на тороидальном каркасе или, при использовании толстого провода и малом числе витков — без каркаса. Иногда, для снижения распределённой паразитной ёмкости, при использовании в качестве высокочастотного дросселя однослойные катушки индуктивности наматываются с «прогрессивным» шагом — шаг намотки плавно изменяется по длине катушки.
Намотка может быть как однослойной (рядовая и с шагом), так и многослойной (рядовая, внавал, типа «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость. Часто, опять же, для снижения паразитной ёмкости, намотку выполняют секционированной, группы витков отделяются пространственно (обычно по длине) друг от друга.

Для увеличения индуктивности катушки часто снабжают замкнутым или разомкнутым ферромагнитным сердечником. Дроссели подавления высокочастотных помех имеют ферродиэлектрические сердечники: ферритовые, флюкстроловые, из карбонильного железа. Дроссели, предназначенные для сглаживания пульсаций промышленной и звуковой частот, имеют сердечники из электротехнических сталей или магнитомягких сплавов (пермаллоев). Также сердечники (в основном ферромагнитные, реже диамагнитные) используют для изменения индуктивности катушек в небольших пределах путём изменения положения сердечника относительно обмотки. На сверхвысоких частотах, когда ферродиэлектрики теряют свою магнитную проницаемость и резко увеличивают потери, применяются металлические (латунные) сердечники.

На печатных платах электронных устройств также иногда делают плоские «катушки» индуктивности: геометрия печатного проводника выполняется в виде круглой или прямоугольной спирали, волнистой линии или в виде меандра. Такие «катушки индуктивности» часто используются в сверхбыстродействующих цифровых устройствах для выравнивания времени распространения группы сигналов по разным печатным проводникам от источника до приемника, например, в шинах данных и адреса.

Терминология

Стандартизированные термины:

Индуктивная катушка — элемент электрической цепи, предназначенный для использования его индуктивности (ГОСТ 19880-74, см. термин 106).

Катушка индуктивности — индуктивная катушка, являющаяся элементом колебательного контура и предназначенная для использования её добротности (ГОСТ 20718-75, см. термин 1).

Электрический реактор — индуктивная катушка, предназначенная для использования её в силовой электрической цепи (ГОСТ 18624-73, см. термин 1). Одним из видов реактора является токоограничивающий реактор, например, для ограничения тока короткого замыкания ЛЭП.

При использовании для подавления помех, сглаживания пульсаций электрического тока, изоляции (развязки) по высокой частоте разных частей схемы и накопления энергии в магнитном поле сердечника часто называют дросселем, а иногда реактором. Стоит отметить, что такое толкование нестандартизированного термина «дроссель» (являющегося калькой с нем. Drossel) пересекается со стандартизированными терминами. В случае если работа данного элемента цепи основана на добротности катушки, то такой элемент следует называть «катушкой индуктивности», в противном случае «индуктивной катушкой».

Цилиндрическую катушку индуктивности, длина которой намного превышает диаметр, называют соленоидом, магнитное поле внутри длинного соленоида однородно. Кроме того, зачастую соленоидом называют устройство, выполняющее механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника, или электромагнитом. В электромагнитных реле называют обмоткой реле, реже — электромагнитом.

Нагревательный индуктор — специальная катушка индуктивности, рабочий орган установок индукционного нагрева.

При использовании для накопления энергии (например, в схеме импульсного стабилизатора напряжения) называют индукционным накопителем или накопительным дросселем.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Маркировка

При рассмотрении катушек индуктивности оценивается цветовая и кодовая маркировка. Если смотреть на первые цифры, отображается показатель индуктивности. Далее учитывается параметр отклонения:

• Серебряный 0,01 мкГн, 10%.
• Золотой 0,1 мкГн, 5%.
• Черный 0,1мкГн, 20%.
• Коричневый 1,1 мкГн.
• Красный 2, 2 мкГн.
• Оранжевый 1 мкГн.
• Желтый 4 мкГн.
• Зеленый 5 мкГн.
• Голубой 6 мкГн.
• Фиолетовый 7мкГн.
• Серый 8 мкГн.
• Белый 9 мкГн.

Маркировка

В нестабильной цепи переменного электрического тока не обойтись без катушки индуктивности. Выше описаны основные типы изолированных проводников, продемонстрированы их параметры. Учитывается уровень частоты, а также свойства.

Приветствую всех на нашем сайте!

Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:

Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:

Собственно, график нам и демонстрирует эту зависимость Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.

Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу

Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: 0″ title=»Rendered by QuickLaTeX.com» />, участок 3-4: 0″ title=»Rendered by QuickLaTeX.com» />,

Где – круговая частота: . – это частота переменного тока.

Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный ( = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.

Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение ? Здесь все на самом деле просто По 2-му закону Кирхгофа:

А следовательно:

Построим на одном графике зависимости тока и напряжения в цепи от времени:

Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:

При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.

Вот и с включением катушки в цепь переменного тока мы разобрались

На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому дальнейший разговор о катушках индуктивности мы будем вести в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!

В данной статье мы подробно рассмотрим индуктор. Отдельно разберем индуктор на схеме, обратную ЭДС генерируемую индуктором, постоянную времени индуктора, ток и напряжение в индукторе, а так же мощность и энергию в индукторе.

2.2 Индуктивное сопротивление катушки

Включить звук

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.

Чисто индуктивное сопротивление отличается от  обычного  (омического)  сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопротивлением, то им можно пренебречь.

При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

Рисунок 2 —  Зависимость индуктивного сопротивления катушки от частоты переменного тока. 

Реактивное сопротивление катушки возрастает с увеличением частоты тока.

Индуктивное сопротивление обозначается буквой X_L и измеряется в Омах.

Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле

X_L = 2π f L,

где X_L — индуктивное сопротивление в Ом;

f—частота переменного тока в Гц;

L — индуктивность катушки в Гн

Как известно, величину 2πf называют угловой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так

X_L = ωL.

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

2.3 Электрические модели реальных катушек индуктивности

Характеристики идеальной катушки индуктивности будут соответствовать индуктивному элементу схемы замещения.

Реальные катушки индуктивности намотаны из провода, имеющего ненулевое удельное сопротивление, таким образом, чем больше витков содержит катушка, тем будет выше её активное сопротивление, которое, обычно, необходимо учитывать во всём диапазоне частот Следует отметить, что на постоянном токе индуктивная составляющая катушки будет равна нулю, и в качестве схемы замещения можно использовать один резистивный элемент (рисунок 3а). С ростом частоты возрастёт индуктивное сопротивление катушки, поэтому в схеме замещения появляется индуктивность (рисунок 3б). Еще на более высоких частотах начинает проявляться влияние межвитковой ёмкости (витки выполнены из изолированного провода, таким образом два соседних можно рассматривать как конденсатор) (рисунок 3в).

На сверхвысоких частотах резко возрастает роль индуктивности и ёмкости выводов катушки индуктивности.

а –– на постоянном токе; б –– на низких частотах; в –– на высоких частотах;

R_к –– активное сопротивление катушки; C_п –– паразитная межвитковая ёмкость

Рисунок 3 —  Схема замещения катушки индуктивности

2.4 Параметры элементов схемы замещения на низких частотах

2.4.1 Индуктивность катушки

Согласно ГОСТ Р 52002-2003 и ГОСТ 20715-75 предусмотрены следующие термины и определения индуктивности.

Собственная индуктивность — это скалярная величина, равная отношению потокосцепления самоиндукции элемента электрической цепи к электрическому току в нем

.

Это понятие относится к одной катушке индуктивности или одному ее элементу, которые является одновременно источником магнитного поля и ее приемником.

 Взаимная индуктивность — скалярная величина, равная отношению потокосцепления взаимной индукции одного элемента электрической цепи к току в другом элементе, обусловливающему это потокосцепление

.

Это понятие относится как минимум к двум катушкам индуктивности или к двум элементам одной катушки, одни из которых являются одновременно источником магнитного поля, а другой — ее приемником и наоборот.

Начальная индуктивность катушки — значение индуктивности, определенное при условии отсутствия влияния собственной емкости, изменения начальной проницаемости сердечника и собственной индуктивности. Начальная индуктивность – это собственная индуктивность идеальной катушки. Индуктивность, максимально приближенная к начальной индуктивности опре­деляется на низкой частоте, где практически отсутствует влияние собствен­ной емкости.

Эффективная индуктивность катушки — значение индуктивности, определенное с учетом влияния собственной емкости, собственной индуктивности и изменения начальной проницаемости сердечника.

В настоящее время частично катушки индуктивности также как резисторы и конденсаторы можно отнести к изделиям общего применения. Они производятся на специализированных предприятиях и предназначены для продажи. Однако много катушек проектируют и производят те предприятия, в изделиях которых предполагается их эксплуатация. То есть такие катушки являются изделиями частного применения.

Для катушек обоих типов существует понятие номинальной индуктивности. Номинальная индуктивность — значение индуктивности, являющееся исходной для отсчета отклонений.

Номинальные индуктивности для катушек общего применения регламентируется обычно рядами Е6 и Е12 с допусками 1 %, 2 %, 5 %, 10 %, 20 % и 30 %.

Номинальные индуктивности и допуски для катушек частного применения определяются результатами электрического расчета, представленным в техническом задании на разработку катушки и регламентируются стандартами предприятий или техническими условиями на конкретную аппаратуру.

На практике под индуктивностью катушки обычно имеют ввиду собственную индуктивность. В РЭА применяются катушки с индуктивностью от долей микрогенри (контурные высокочастотные) до десятков генри (дроссели фильтров выпрямителей). Контурные катушки по величине индуктивности изготовляются с точностью от 0,2 до 0,5%, а для других катушек индуктивности допустима точность до 30 %.

Индуктивность катушки пропорциональна линейным размерам обмотки катушки, магнитной проницаемости сердечника, квадрату числа витков намотки и соотношению размеров экрана и обмотки.

В зависимости от вида и типа обмотки существуют различные аналитические или графические алгоритмы расчета ее параметров.

Из теоретической электротех­ники известно следующее выражение для индуктивности длинного соленоида круглого сечения (предполагается = 1)

,

где — магнитная постоянная;

— относительная магнитная проницаемость материала;

— число витков

— длина магнитной силовой линии. Это выражение дает достаточно точный (до 2%) резуль­тат лишь для соленоидов, длина которых от 20 до 30 раз больше диаметра, со сплошной намоткой проводом, имею­щим бесконечно тонкую изоляцию. В реальных соленои­дах (катушках) длина обычно соизмерима с диаметром. Благодаря этому магнитное поле у концов катушки искрив­ляется, крайние витки сцепляются с меньшим числом магнитных силовых линий и фактическая индуктивность оказывается меньше расчетной.

Точный учет этого явления приводит к громоздким, неудобным для практики выражениям. Поэтому для про­стоты в расчетные формулы вводят поправочные коэффи­циенты, величина которых зависит от отношения . Наиболее удобной является следующая формула

,

где — индуктивность, мкГн; —диаметр катушки, см. Значения поправочных коэффициентов для одно­слойных катушек определяются из графиков = f( ).

Практическое руководство по катушкам индуктивности

Большинство проводящих материалов (металлов) является парамагнитными или ферромагнитными, в то время как большинство непроводящих материалов (неметаллов) является диамагнитными. Любой проводник обладает некоторой индуктивностью в ответ на изменение величины или направления протекания тока. Даже обычный прямой провод имеет индуктивность, хотя она достаточно мала, чтобы пренебрегать ею. Если провод свернуть в петлю — его индуктивность увеличится. Чем больше сделать таких одинаковых витков, тем большая индуктивность будет присуща проводу. Индуктивность одиночной петли или катушки из провода может быть многократно увеличена с помощью подходящего ферромагнитного сердечника.

Простейшими катушками индуктивности являются катушки с воздушным сердечником (рисунок 1). Они сделаны путем намотки провода вокруг пластмассового, деревянного или любого не ферромагнитного сердечника. Индуктивность катушки зависит от числа витков, радиуса и общей формы, также она пропорциональна числу витков и диаметру катушки. Индуктивность обратно пропорциональна длине провода для заданного диаметра катушки и числу витков. Итак, чем ближе будут витки, тем больше будет индуктивность. Электропроводность катушек индуктивности зависит от материала и толщины провода. Потери (в виде тепла) в значительной степени зависят от материала, используемого в качестве сердечника.

 

Рис. 1. Пример катушки индуктивности с воздушным сердечником 

Катушки с воздушным сердечником имеют небольшую индуктивность, которая может составлять максимум 1 мГн. Катушки с воздушным сердечником могут быть рассчитаны так, что будут пропускать через себя ток практически неограниченной величины при условии использования проводника большой длины, смотанного в катушку большого радиуса. Такие катушки индуктивности практически не вносят потерь, так как воздух не рассеивает много энергии в виде тепла. Чем выше частота переменного тока, тем меньше индуктивность, необходимая для получения значительных эффектов. Таким образом, катушки индуктивности с воздушным сердечником вполне подходят для применения в высокочастотных цепях переменного тока благодаря отсутствию потерь, способности пропускать через себя большие токи и достаточным значениям индуктивности.

При использовании железных или ферритовых сердечников индуктивность может быть значительно увеличена. Однако порошкообразный, железный или ферритовый сердечник вносит значительные потери электрической энергии в виде тепла. Использование ферромагнитных сердечников также ограничивает максимальную величину рабочего тока катушек индуктивности. В ферромагнитных сердечниках насыщение происходит при протекании максимального рабочего тока. При увеличении тока сверх этого критического значения индуктивность может начать уменьшаться. При больших токах ферромагнитные сердечники могут достаточно сильно нагреваться, что может привести к их разрушению и необратимому существенному изменению номинальной индуктивности катушки.

Соленоид против катушек индуктивности

 

Соленоиды часто путают с катушками индуктивности. Соленоиды — это катушки проводов, которые предназначены для использования в качестве электромагнитов. Многие индукторы также являются катушками проводов, но они предназначены для обеспечения индуктивности в электрической цепи. Катушки индуктивности цилиндрической формы также называют соленоидными катушками, но только из-за их конструкции, схожей с конструкцией соленоида. Тем не менее, они не предназначены для использования в качестве электромагнита. Соленоиды специально используются в качестве электромагнитов и обычно имеют подвижный или статический сердечник. Обычно соленоиды используются в качестве электромагнитов в электрических звонках, электродвигателях, работающих на постоянном токе, и в реле.

Соленоидные катушки как индуктивности

 

Простейшими и наиболее распространенными индуктивностями являются соленоидные катушки. Эти индуктивности представляют собой цилиндрические катушки, намотанные вокруг диамагнитного или ферромагнитного сердечника. Они являются самыми простыми с точки зрения проектирования и изготовления.

Соленоидная, или цилиндрическая катушка может быть легко использована для подстройки величины индуктивности, если в конструкцию интегрировать механизм перемещения ферромагнитного сердечника катушки внутрь и наружу. Путем перемещения сердечника внутрь катушки и обратно можно изменять ее эффективную магнитную проницаемость и, следовательно, величину индуктивности. Это называется настройкой магнитной проницаемости и используется для подстройки частот в радиочастотных схемах.

Сердечник можно сделать подвижным, прикрепив его к винтовому валу и закрепив гайкой на другом конце катушки. Когда вал винта вращается по часовой стрелке — сердечник перемещается внутрь катушки, увеличивая эффективную магнитную проницаемость и, следовательно, величину индуктивности. Когда вал винта вращается против часовой стрелки — сердечник выдвигается, уменьшая эффективную магнитную проницаемость и, следовательно, величину индуктивности.

Тороиды как катушки индуктивности

Сегодня еще одной наиболее распространенной формой катушек индуктивности является тороид. Тороиды имеют кольцевой ферромагнитный сердечник, на который намотан провод. Тороиды нуждаются в меньшем числе витков и физически меньше при той же величине индуктивности и рабочей величине тока, по сравнению с соленоидными катушками (рисунок 2). Другим важным преимуществом тороидов является то, что магнитный поток находится внутри сердечника, что позволяет избежать нежелательной взаимной индуктивности.

Рис. 2. Сильноточные тороидальные катушки индуктивности 

Однако намотать провод на тороид сложно. Регулировать магнитную проницаемость тороида еще сложнее. Проектирование катушек с тороидальным сердечником и переменной величиной индуктивности требует реализации громоздкой и сложной конструкции. В цепях, где требуется взаимная индуктивность, катушки должны быть намотаны на один и тот же сердечник в случае, если тороид используется в качестве катушки индуктивности.

Индуктивности на основе чашеобразных Р-сердечников*

 

В типичных катушках индуктивности — соленоидных и тороидных — провод намотан вокруг ферромагнитного сердечника. Катушки индуктивности на основе чашеобразных сердечников – это другой тип индуктивностей, в котором обмотка катушки находится внутри ферромагнитного сердечника. Чашеобразный ферромагнитный сердечник имеет форму двух половин в виде чаш со специальным цилиндрическим выступом (керном) на дне одной из половин, на котором размещается обмотка. Обе половины имеют отверстия, из которых извлекается провод катушки. Вся сборка скрепляется болтом и гайкой.

Катушки данного типа, как и тороиды, обладают большой индуктивностью и электропроводностью при небольших габаритах и меньшем числе витков. Магнитный поток, как и в случае с тороидами, остается внутри. Таким образом, нет нежелательной взаимной индуктивности с сердечниками. Опять же, как и в случае с тороидами, очень трудно варьировать величину индуктивности катушек данного типа. Изменять величину индуктивности в катушках индуктивности на основе Р-сердечников возможно только путем изменения числа витков и при использовании отводов в разных точках катушки.

*- В литературе также встречается термин “Р-сердечник закрытого типа”. В ГОСТ 19197-73 данному типу сердечников присвоено название – “броневой”.

Линия передачи как индуктивность

В цепях постоянного тока катушки индуктивности ведут себя почти так же, как и обычный провод, обладая незначительным сопротивлением, но не более того. Таким образом, они находят применение преимущественно в электрических цепях переменного тока. В аудиосхемах в качестве индуктивностей обычно используются тороиды, катушки на основе круглых чашеобразных сердечников или аудиотрансформаторы. Номинал индуктивности, применяемый в таких электрических цепях, варьируется от нескольких мГн до 1 Гн. Катушки индуктивности вместе с конденсаторами используются в аудиосхемах для подстройки. В настоящее время микросхемы практически полностью вытеснили катушки индуктивности и конденсаторы в аудиосистемах и других подобных областях применения.

При увеличении частоты должны использоваться индуктивности с сердечниками меньшей проницаемости. На нижнем конце радиочастотного спектра используются те же катушки индуктивности, что и в аудиоприложениях. На частотах до нескольких МГц весьма распространены катушки индуктивности с тороидальным сердечником. Для частот 30…100 МГц предпочтительны катушки с воздушным сердечником. Для частот более 100 МГц в линии передачи используются высокочастотные индуктивности и специальные трансформаторы. Линии передачи малой длины (четверть длины волны сигнала или меньше) сами могут быть использованы в качестве индуктивности для подстройки частоты радиосигналов. Линия передачи, используемая в качестве подобной индуктивности, обычно представляет собой коаксиальный кабель.

Индуктивности в цепях постоянного тока

Катушки индуктивности практически бесполезны в цепях постоянного тока. Однако можно предположить, что катушка индуктивности, подключенная к цепи постоянного тока, может быть полезна для понимания принципов ее работы и особенностей поведения пульсирующих напряжений постоянного тока. Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:

V_L = – L*(di/dt),   (1)

где:

• V_L – напряжение (обратная ЭДС), индуцированная на катушке;
• L – индуктивность катушки;
• di/dt – скорость изменения тока во времени.

Согласно приведенной формуле 1, внезапное изменение тока через катушку индуктивности дает бесконечное напряжение, что физически невозможно. Таким образом, ток через катушку индуктивности не может измениться мгновенно. Ток сталкивается с влиянием индуктивности при каждом небольшом изменении его величины и медленно возрастает до своего пикового постоянного значения. Итак, в начальный момент времени катушка индуктивности представляет собой разрыв цепи, когда переключатель замкнут. Обратная ЭДС наводится на катушку индуктивности до тех пор, пока изменяется значение протекающего через нее тока. Индуцированная обратная ЭДС всегда остается равной и противоположной возрастающему приложенному напряжению. Когда напряжение и ток от источника приближаются к постоянному значению, обратная ЭДС падает до нуля, а катушка индуктивности начинает вести себя как обычный провод. При подаче напряжения на катушку индуктивности мощность, запасенная ею, определяется по формуле 2:

P = V * I = L*i*di/dt,   (2)

где:

• P – электрическая мощность, запасенная в катушке;
• V – величина пикового напряжения на катушке индуктивности;
• I – величина пикового тока, протекающего через катушку индуктивности.

Энергия, запасенная индуктивностью при подаче напряжения, определяется по формуле 3:

W = ∫P.dt = ∫L*i*(di/dt)dt = (1/2)LI²,   (3)

где:

• W – электрическая энергия, запасенная в катушке индуктивности в виде магнитного поля;
• I – максимальное значение тока, протекающего через катушку.

Когда происходит отключение источника напряжения (путем размыкания ключа), напряжение на индуктивности падает с постоянного пикового значения до нуля. В отличие от конденсаторов, при отключении источника напряжения напряжение на индуктивности не поддерживается. Фактически оно уже упало до нуля, тогда как ток, проходящий через него стал постоянным. Теперь, когда приложенное напряжение падает от пикового постоянного значения до нуля, ток, протекающий через катушку индуктивности, также падает с постоянного пикового значения до нуля. Катушка противодействует падению тока, вызывая прямую ЭДС в направлении приложенного напряжения. Из-за индуцированной прямой ЭДС ток, проходящий через катушку индуктивности, падает до нуля с более медленной скоростью. Как только ток уменьшается до нуля, прямая ЭДС также падает до нуля.

Таким образом, при подаче напряжения питания электрическая энергия преобразовывалась в магнитное поле в катушке индуктивности, что было очевидно по обратной ЭДС, индуцированной на ней. При отключении напряжения питания та же самая электрическая энергия возвращается индуктором в цепь в форме прямой ЭДС. Всякий раз, когда напряжение на катушке индуктивности увеличивается, возникает обратная ЭДС, а всякий раз, когда напряжение на катушке уменьшается, возникает прямая ЭДС.

На практике обратная или прямая ЭДС, которая наводится на катушке индуктивности, во много раз больше приложенного напряжения. Если источник индуктивности подключен к источнику напряжения или катушка индуктивности подключена к цепи постоянного тока без какой-либо защиты, электрическая энергия, возвращаемая при размыкании переключателя, выделяется в виде скачка напряжения или искры на контактах переключателя. Если индуктивность или ток в цепи достигают достаточно больших значений, то энергия выделяется в форме дуги или искры на контакте переключателя и может даже сжечь или расплавить его. Этого можно избежать, используя резистор и конденсатор, соединенные в RC-цепь и включенные последовательно с контактом переключателя. Такая RC-цепь называется снабберной и позволяет электрической энергии, выделяемой катушкой индуктивности, заряжать и разряжать конденсатор, поэтому она не повреждает другие компоненты. Во многих электрических цепях для сохранения компонентов схемы от обратной или прямой ЭДС катушек индуктивности или соленоидов используются защитные диоды.

Катушка индуктивности в цепи переменного тока

Катушка индуктивности противодействует любому изменению тока, который протекает через нее, а переменный ток, в свою очередь, отстает на 90° от напряжения. В начальный момент времени, когда напряжение источника подается на катушку, ток через нее протекает максимальный, но в противоположном направлении. При подаче напряжения ток протекает через катушку индуктивности из-за индуцированной обратной ЭДС, которая противоположна приложенному напряжению. Индуцированное на катушке напряжение всегда равно и противоположно по знаку приложенному напряжению в любой момент времени. Когда приложенное напряжение возрастает от нуля до пикового значения, ток через катушку падает от максимума до нуля.

Когда прикладываемое напряжение падает от максимального значения до нуля, то на катушке индуцируется прямая ЭДС, заставляя ток противоположного направления расти от нуля до пикового значения. Когда приложенное напряжение меняет полярность и возрастает до пикового значения, ЭДС снова индуцируется на катушке, вызывая падение обратного тока от пикового значения до нуля. Когда приложенное напряжение снова падает до нуля в обратном направлении, в катушке индуцируется прямая ЭДС, заставляющая ток снова расти от нуля до максимального значения в противоположном направлении. Это продолжается для каждого цикла протекания переменного тока.

Индуктивное сопротивление

Противодействие протекающему току из-за наличия индуктивности называется индуктивным сопротивлением. Амплитуда тока через катушку индуктивности обратно пропорциональна частоте приложенного напряжения. Поскольку напряжение на катушке (обратная или прямая ЭДС) пропорционально индуктивности, то амплитуда тока также обратно пропорциональна величине индуктивности. Итак, противодействие току из-за наличия индуктивности в виде индуктивного сопротивления определяется по формуле 4:

X_L = 2πfL= ωL   (4)

Соответственно, пиковая амплитуда тока, проходящего через катушку индуктивности, определяется по формуле 5:

I_peak = V_peak/X_L= V_peak/ ωL,   (5)

где:

• I_peak – пиковое значение переменного тока, протекающего через катушку индуктивности;
• V_peak – пиковое значение переменного напряжения, приложенного к катушке;
• X_L – индуктивное сопротивление.

Как резистивное и емкостное сопротивление, так и единица индуктивного сопротивления измеряется в омах. Следует отметить, что в электрических цепях нет потерь энергии из-за наличия емкостного или индуктивного сопротивления, что нельзя сказать об обычном резистивном сопротивлении. Тем не менее, реактивное сопротивление может ограничивать уровни тока через конденсатор или катушку индуктивности.

Применение катушек индуктивности

Катушки индуктивности используются в электрических цепях переменного тока. Они обычно применяются в аналоговых схемах, схемах обработки сигналов и в системах телекоммуникаций, а также используются вместе с конденсаторами для создания фильтров различных топологий. В телекоммуникационных системах индуктивности применяются в составе специальных фильтров, которые нужны для подавления возможных бросков напряжения и предотвращения утечки информации через линии системы электропитания.

Трансформаторы, которые используются для повышения или понижения напряжения переменного тока, состоят из двух катушек индуктивности, объединенных в единую конструкцию определенным образом. Индуктивности также используются для временного хранения электрической энергии в цепях выборки-хранения и источниках бесперебойного питания. В цепях электропитания катушки индуктивности (где они называются фильтрующими дросселями) используются для сглаживания пульсирующих токов.

Поведение индуктивности при прохождении через нее сигнала можно определить следующим образом:

• Всякий раз, когда приложенное к катушке индуктивности напряжение увеличивается, катушка генерирует обратную ЭДС, в результате чего ток через нее падает с максимального значения до нуля или даже ниже этого уровня. Всякий раз, когда прикладываемое напряжение уменьшается, катушка создает прямую ЭДС, в результате чего ток через нее повышается с нуля или текущего уровня до максимального значения или даже до более высокого.
• Обратная или прямая ЭДС сохраняется на катушке индуктивности до тех пор, пока приложенное напряжение, а следовательно и ток через нее изменяются. Когда приложенное напряжение достигает определенного постоянного значения, обратная или прямая ЭДС падает до нуля, и постоянный ток протекает через катушку индуктивности без какого-либо противодействия, как в обычном соединительном проводе.
• Из-за наличия индуктивности скорость изменения тока в цепи замедляется. Если сигнал переменный, то ток всегда будет отставать от напряжения на 90° из-за наличия индуктивности.
• Благодаря индуктивному или емкостному сопротивлению потери энергии отсутствуют. Энергия, запасенная катушкой индуктивности в форме магнитного поля или конденсатором в форме электростатического поля, возвращается обратно в цепь, как только приложенное напряжение падает до нуля или меняет полярность. Однако из-за реактивного сопротивления пиковый уровень тока (амплитуда сигнала) ограничен.

Источник: https://www.engineersgarage.com

Увеличение — частота — ток

Увеличение — частота — ток

Cтраница 2

При увеличении частоты тока, проходящего через катушку, магнитная проницаемость цс уменьшается, а потери, вносимые сердечником гс, растут.  [16]

При увеличении частоты тока, текущего через катушку, магнит-ная проницаемость ] лс уменьшается, а потери, вносимые сердечником гс, растут.  [17]

При увеличении частоты тока, текущего через катушку, магнитная проницаемость лс уменьшается, а потери, вносимые сердечником гс, растут.  [19]

При увеличении частоты токов, протекающих через цепочку, ее сопротивление увеличивается. Если для низких и средних частот сопротивлением индуктивности o) La из-за его малой величины можно пренебречь, то в области высших частот это сопротивление оказывается достаточно большим. Полное сопротивление нагрузки, включающее в себя активное сопротивление резистора Ra, корректирующую индуктивность La и паразитную емкость Спйр, уменьшаясь из-за действия паразитной емкости и увеличиваясь за счет действия корректирующей индуктивности, остается постоянным по величине в более широкой области частот.  [21]

При увеличении частоты тока глубина его проникновения в организм человека уменьшается и соответственно уменьшается опасность несчастных случаев. Ток высокой частоты распространяется главным образом по поверхности тела, вызывая ожоги.  [22]

Однако при увеличении частоты тока внутреннее индуктивное сопротивление провода возрастает не пропорционально частоте тока, как, казалось бы, следует из выражения xL ( dL, но для больших частот приблизительно пропорционально корню квадратному из частоты.  [23]

Следовательно, при увеличении частоты тока внутренняя индуктивность проводов цепей связи уменьшается и приближается к величине внешней индуктивности.  [25]

Коэффициент затухания возрастает при увеличений частоты тока. Для бро-норованного кабеля затухание мало зависит от того, намотан ли кабель на барабан лебедки или спущен в скважину.  [26]

Известно, что с увеличением частоты тока возрастает скин-эффект; плотность тока в наружных слоях проводника оказывается во много раз большей, чем в сердцевине. В результате почти вся тепловая энергия выделяется в поверхностном слое и вызывает его разогрев.  [28]

Таким образом, при увеличении частоты тока глубина протекания токов уменьшается, следовательно, с увеличением частоты тока растет сопротивление земли. При протекании же переменного тока сопротивление земли, как отмечалось, увеличивается.  [30]

Страницы:      1    2    3    4    5

цепей переменного тока | Безграничная физика

Индуктивность

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.

Цели обучения

Опишите свойства индуктора

Основные выводы

Ключевые моменты

• В случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
• Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
• Взаимная индуктивность обозначена. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
• Самоиндукция — это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
• Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.

Ключевые термины

• взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
• самоиндукция : Отношение напряжения к изменению тока в той же цепи.
• индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.

Индуктивность

ОБЗОР

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность).Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, с изменяющимся током, усиливающим изменение тока). петля положительной обратной связи).

ВЗАИМНАЯ ИНДУКТИВНОСТЬ

Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.

Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]

, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность М, , тем эффективнее связь. Единицы измерения для M : (V⋅s) / A = Ωs, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.

Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] \ text {emf} _1 = — \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]

, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью М.

Большая взаимная индуктивность M, может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля.(Видеть ).

Противоточная намотка : Нагревательные катушки электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по отношению к корпусу сушилки.

САМОИНДУКЦИЯ

Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]

, где L — собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.

.

Обозначение индуктора

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.

СОЛЕНОИДЫ

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L, обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).

Поучительно вывести это уравнение, но это оставлено читателю в качестве упражнения. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением. {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].

Ключевые термины

• характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R — сопротивление, а L — индуктивность. Когда переключатель замкнут, это время, необходимое для того, чтобы сила тока уменьшилась с коэффициентом 1 / e.
• индуктор : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.

Цепи RL

Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.

Обзор

Напомним, что индукция — это процесс, в котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность — это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция — это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности — это устройство или компонент схемы, который демонстрирует самоиндукцию.

Энергия индуктора

Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].

Катушки индуктивности в цепях

Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет потоком, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.

Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещается в положение 2.

Когда переключатель впервые перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге возрастает до I ₀ = В / R , где R — полное сопротивление цепи, а V — напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]

— это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I ₀ = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :

[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],

, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I ₀ , поскольку I = I ₀ (1 − e ⁻¹ ) = I ₀ ( 1−0,368) = 0,632I ₀ . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных промежутков времени [latex] \ tau [/ latex] конечное значение почти достигнуто (см. Часть (b) на рисунке выше).

Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы добраться до него. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.

Когда переключатель в (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, создавая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI ₀ ² , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I ² R.{\ frac {- \ text {t}} {\ tau}} [/ latex]

В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от своего начального значения, поскольку I = I ₀ e ⁻¹ = 0,368I ₀ . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.

Цепь серии

RLC: на больших и малых частотах; Фазорная диаграмма

Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.

Цели обучения

Различать поведение цепей серии RLC на больших и малых частотах

Основные выводы

Ключевые моменты

• RLC-схемы можно описать (обобщенным) законом Ома. Что касается фазы, когда прикладывается синусоидальное напряжение, ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
• На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
• На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока с конденсатор. Следовательно, среднеквадратичный ток будет выражен как V _rms / X _C, , а ток опережает напряжение почти на 90 ^∘ .

Ключевые термины

• Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
• резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.

В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Комбинируя закон Ома (I _{действующее значение} = В _{действующее значение} / Z; I _{действующее значение} и В _{среднеквадратичное значение} являются среднеквадратичным значением тока и напряжения) и выражения для импеданса Z из:

Цепь последовательного RLC : Последовательная цепь RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].

Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при приложении синусоидального напряжения ток отстает от напряжения на фазу 90º в цепи с катушкой индуктивности, в то время как ток опережает напряжение на 90 ^∘ . в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.

на больших частотах

На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], X _L намного больше, чем X _C .Если частота достаточно высока, так что X _L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [латекс] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним индуктором. Следовательно, среднеквадратичный ток будет составлять _В / X _L , а ток отстает от напряжения почти на 90 ^∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление катушки индуктивности будет большим.

на малых частотах

В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостной член, предполагая, что частота достаточно высока, так что X _C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичный ток будет выражен как V _rms / X _C, , а ток опережает напряжение почти на 90 ^∘ .

Резисторы в цепях переменного тока

В цепи с резистором и источником питания переменного тока все еще действует закон Ома ( В, = IR ).

Цели обучения

Применить закон Ома для определения силы тока и напряжения в цепи переменного тока

Основные выводы

Ключевые моменты

• При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].

Ключевые термины

• Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.

Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая обслуживает так много наших потребностей. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.

Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.

Мы изучили закон Ома:

[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]

, где I, — ток, В, — напряжение, а R, — сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, с напряжением переменного тока, определяемым по формуле:

[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]

, где В ₀ — пиковое напряжение, а [латекс] \ nu [/ latex] — частота в герцах, ток в цепи определяется как:

[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]

В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b). 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]

Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ латекс]

Конденсаторы

в цепях переменного тока: емкостное сопротивление и фазовые диаграммы

Напряжение на конденсаторе отстает от тока. Из-за разности фаз для описания этих схем полезно вводить векторы.

Цели обучения

Объясните преимущества использования векторного представления

Основные выводы

Ключевые моменты

• Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
• Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
• Среднеквадратичное значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] — это емкостное реактивное сопротивление.

Ключевые термины

• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.

В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.

Конденсаторы в цепях переменного тока с фазорами

Фазор

Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.

Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса — это проекция вектора на действительную ось. Его амплитуда — это модуль вектора, а его аргумент — полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.

Конденсаторы в цепях переменного тока

Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.

Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ». Это показано на.

Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.

Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V _max / I _max полезно и называется емкостным реактивным сопротивлением (X _C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X _C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].

Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I _{, действующее значение} в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V _rms — это действующее значение напряжения. Обратите внимание, что X _C заменяет R в версии закона Ома для постоянного тока.

Фазовое представление

Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.

Рис. 4 : Векторная диаграмма для цепи переменного тока с конденсатором

Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы

В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.

Цели обучения

Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности

Основные выводы

Ключевые моменты

• С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90º.
• Среднеквадратичное значение тока I _{среднеквадратичное значение} через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X _L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
• Фазоры — это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.

Ключевые термины

• Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
• phasor : представление комплексного числа в виде комплексной экспоненты.

Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).

Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I _rms через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V _rms — среднеквадратичное значение напряжения на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X _L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X _L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, имеет единицы (циклов / с) (Ом · с) = Ом), что соответствует его роли в качестве эффективное сопротивление.

Представление векторов

Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора — это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.

Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.

Фазоры для индукторов в цепях переменного тока

Резонанс в цепях RLC

Резонанс — это тенденция системы к колебаниям с большей амплитудой на некоторых частотах — в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].

Цели обучения

Сравнить резонансные характеристики цепей с высоким и низким сопротивлением

Основные выводы

Ключевые моменты

• Условие резонанса последовательной цепи RLC может быть получено приравниванием X _L и X _C , так что два противоположных вектора компенсируют друг друга.
• В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I _{среднеквадратичное значение} является максимальным.
• Цепи с более высоким сопротивлением не так сильно резонируют по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.

Ключевые термины

• реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
• импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.

Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],

, где I _rms и V _rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], причем X _L большое на высоких частотах и ​​X _C большое на низких частотах, представленное как:

[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].

На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I _rms результатов.Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X _L = X _C . Подстановка определений X _L и X _C дает:

[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].

[латекс] \ nu_0 [/ latex] — это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I _rms является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.

Приемник в радиостанции представляет собой схему RLC, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I _rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным цепям, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.

Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.

Мощность

Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и задается как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.

Цели обучения

Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.

Основные выводы

Ключевые моменты

• Фазовый угол ϕ — это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
• На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
• Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.

Ключевые термины

• rms : Среднеквадратичное значение: статистическая мера величины переменной величины.

Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных схемах. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный

.

[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на схеме.

Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi — фазовый угол, равный разности фаз между напряжением и током.

Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I _rms ниже.

Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность

[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]

(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) — ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при проектировании эффективного двигателя. На резонансной частоте cosϕ = 1.

Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).

Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке. Равномерно расположенные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.

Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.

Индуктивность — высокочастотные эффекты

График Найквиста, показывающий поведение высокочастотной индукции.

Влияние индуктивностей часто наблюдается на самых высоких частотах. В Импеданс катушки индуктивности увеличивается с увеличением частоты, а сопротивление конденсатора уменьшается.Высокий частотно-индуктивное поведение имеет несколько возможных причин. Легче всего визуализировать фактическая физическая индуктивность проводов и, возможно, самого электрода. Я был удивлен, обнаружив индуктивность прямой кусок проволоки! Поскольку рабочий электродный узел часто имеет длинную проволоку или стержень между реальной поверхностью электрода и соединения потенциостата, это может быть важно, если сопротивление электрода низкое.

Некоторые батареи, сформированные свернув тонкий «сэндвич» анод-электролит-катод в компактный цилиндр, можно показать эти эффекты.Эти «паразитные» индуктивности обычно составляют всего несколько микрогенри (мкГн). Тем не мение, поскольку полное сопротивление батарей часто бывает низким, эти отклонения могут быть важны.

Инструментальные артефакты

Высокочастотное индуктивное поведение также может быть вызвано инструментальным артефакты, особенно емкость, связанная с резистором для измерения тока (см. ссылки). Многие производители потенциостатов уже внесли поправки на этот эффект в свои EIS. программное обеспечение. Этот артефакт можно идентифицировать по тому факту, что очевидное индуктивность изменяется каждый раз при изменении диапазона тока.

Другой источник высокочастотных индуктивных поведение — взаимная индуктивность проводов, соединяющих потенциостат с сотовый. Переменный ток, протекающий в противоэлектроде и работающий электродные выводы создают магнитное поле, окружающее провода. Это изменяющееся во времени магнитное поле индуцирует напряжение в опорной точке и рабочий смысл (называемый RE2 некоторыми производителями потенциостатов) ведет. Это наблюдается как высокочастотное индуктивное поведение. Потому что эффект является магнитным, использование экранированных проводов или коаксиального кабеля не устраняет этот эффект.Индуктивности часто находятся в диапазоне 50-500 нГн. Эти эффекты могут быть сводятся к минимуму скручиванием проводов и их правильным размещением. В оставшийся эффект трудно «откалибровать», если только положение проводов строго контролируется и воспроизводимо. Движущийся провода изменят наблюдаемую индуктивность.

БОЛЬШЕ

ССЫЛКИ
«Корректировка срабатывания потенциостата», Техническая записка 201, Принстон Прикладное исследование.
«Поправка на отклик потенциостата при измерениях импеданса», Р. С. Роджерс и В. Дж. Эггерс, Документ № 228, 183-е собрание Общества электрохимиков, Гонолулу, Гавайи, май 1993 г.
«Измерение импеданса с реальным Потенциостаты: поправки на потенциостат Ответ », RS Rodgers, Paper # 134, 2nd International Symposium on Electrochemical Impedance. Спектроскопия, Санта-Барбара, Калифорния, июль 1992 г.

Поставщики и ресурсы радиочастотной беспроводной связи

О компании «Мир радиочастотной беспроводной связи»

Веб-сайт RF Wireless World является домом для поставщиков и ресурсов радиочастотной и беспроводной связи. На сайте представлены статьи, руководства, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тестирование и измерения, калькуляторы, новости, книги, загрузки и многое другое.

Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, волоконная оптика, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. Д. Эти ресурсы основаны на стандартах IEEE и 3GPP. В нем также есть академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и MBA.

статей о системах на основе Интернета вещей

Система обнаружения падений для пожилых людей на основе Интернета вещей : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей.В нем упоминаются преимущества или преимущества системы обнаружения падений Интернета вещей. Читать дальше➤
Также обратитесь к другим статьям о системах на основе Интернета вещей следующим образом:
• Система очистки туалетов самолета. • Система измерения столкновений • Система отслеживания скоропортящихся продуктов и овощей • Система помощи водителю • Система умной торговли • Система мониторинга качества воды. • Система Smart Grid • Система умного освещения на базе Zigbee • Умная парковка на базе Zigbee • Система умной парковки на основе LoRaWAN

---

RF Статьи о беспроводной связи

В этом разделе статей представлены статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE / 3GPP и т. Д. .стандарты. Он также охватывает статьи, относящиеся к испытаниям и измерениям, по тестированию на соответствие, используемым для испытаний устройств на соответствие RF / PHY. УКАЗАТЕЛЬ СТАТЬИ ДЛЯ ССЫЛКИ >>.

---

Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH рассмотрена поэтапно. Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP. Читать дальше➤

---

Основы повторителей и типы повторителей : В нем объясняются функции различных типов ретрансляторов, используемых в беспроводных технологиях.Читать дальше➤

---

Основы и типы замирания. Читать дальше➤

---

Архитектура сотового телефона 5G : В этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G Архитектура сотового телефона. Читать дальше➤

---

Основы помех и типы помех: В этой статье рассматриваются помехи по соседнему каналу, помехи в совмещенном канале, Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. Д.Читать дальше➤

---

5G NR Раздел

В этом разделе рассматриваются функции 5G NR (New Radio), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. Д. 5G NR Краткий указатель ссылок >>
• Мини-слот 5G NR • Часть полосы пропускания 5G NR • 5G NR CORESET • Форматы DCI 5G NR • 5G NR UCI • Форматы слотов 5G NR • IE 5G NR RRC • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • Эталонные сигналы 5G NR • 5G NR m-последовательность • Золотая последовательность 5G NR • 5G NR Zadoff Chu Sequence • Физический уровень 5G NR • Уровень MAC 5G NR • Уровень 5G NR RLC • Уровень 5G NR PDCP

---

Учебные пособия по беспроводным технологиям

В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводной связи.Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, WLAN, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. Д. См. УКАЗАТЕЛЬ Учебников >>

---

Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы по технологии 5G:
Учебное пособие по основам 5G Частотные диапазоны руководство по миллиметровым волнам Волновая рама 5G мм Зондирование волнового канала 5G мм 4G против 5G Испытательное оборудование 5G Сетевая архитектура 5G Сетевые интерфейсы 5G NR канальное зондирование Типы каналов 5G FDD против TDD Разделение сети 5G NR Что такое 5G NR Режимы развертывания 5G NR Что такое 5G TF

---

Этот учебник GSM охватывает основы GSM, архитектуру сети, элементы сети, системные спецификации, приложения, Типы пакетов GSM, структура или иерархия кадров GSM, логические каналы, физические каналы, Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM, установка вызова или процедура включения питания, MO-вызов, MT-вызов, VAMOS, AMR, MSK, модуляция GMSK, физический уровень, стек протоколов, основы работы с мобильным телефоном, Планирование RF, нисходящая линия связи PS-вызовов и восходящая линия связи PS-вызовов.
➤Подробнее.

LTE Tutorial , охватывающий архитектуру системы LTE, охватывающий основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он обеспечивает связь с обзором системы LTE, радиоинтерфейсом LTE, терминологией LTE, категориями LTE UE, структурой кадра LTE, физическим уровнем LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, передача голоса по LTE, расширенный LTE, Поставщики LTE и LTE vs LTE продвинутые.➤Подробнее.

---

RF Technology Stuff

Эта страница мира беспроводной радиосвязи описывает пошаговое проектирование преобразователя частоты RF на примере преобразователя RF UP от 70 МГц до диапазона C. для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO, колодки аттенюатора. ➤Подробнее.
➤Проектирование и разработка радиочастотного трансивера ➤Конструкция RF-фильтра ➤Система VSAT ➤Типы и основы микрополосковой печати ➤ОсновыWaveguide

---

Секция испытаний и измерений

В этом разделе рассматриваются контрольно-измерительные ресурсы, испытательное и измерительное оборудование для тестирования DUT на основе Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.УКАЗАТЕЛЬ испытаний и измерений >>
➤Система PXI для T&M. ➤ Генерация и анализ сигналов ➤Измерения слоя PHY ➤Тест устройства на соответствие WiMAX ➤ Тест на соответствие Zigbee ➤ Тест на соответствие LTE UE ➤Тест на соответствие TD-SCDMA

---

Волоконно-оптическая технология

Оптоволоконный компонент , основные сведения, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель, фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д.Эти компоненты используются в оптоволоконной связи. Оптические компоненты INDEX >>
➤Учебник по оптоволоконной связи ➤APS в SDH ➤SONET основы ➤SDH Каркасная конструкция ➤SONET против SDH

---

Поставщики, производители радиочастотных беспроводных устройств

Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений, см. ИНДЕКС поставщиков >>.

Поставщики радиочастотных компонентов, включая радиочастотный изолятор, радиочастотный циркулятор, радиочастотный смеситель, радиочастотный усилитель, радиочастотный адаптер, радиочастотный разъем, радиочастотный модулятор, радиочастотный трансивер, PLL, VCO, синтезатор, антенну, генератор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексор, дуплексер, микросхема резистора, микросхема конденсатора, микросхема индуктивности, ответвитель, оборудование ЭМС, программное обеспечение для проектирования радиочастот, диэлектрический материал, диод и т. д.Производители RF компонентов >>
➤Базовая станция LTE ➤RF Циркулятор ➤RF Изолятор ➤Кристаллический осциллятор

---

MATLAB, Labview, встроенные исходные коды

Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW. Эти коды полезны для новичков в этих языках. ИНДЕКС ИСХОДНОГО КОДА >>
➤3-8 декодер кода VHDL ➤Код MATLAB для дескремблера ➤32-битный код ALU Verilog ➤T, D, JK, SR триггеры labview коды

* Общая информация о здоровье населения *

Выполните эти пять простых действий, чтобы остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: часто мойте их
2. КОЛЕНО: Откашляйтесь.
3. ЛИЦО: Не трогай его
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВОВАТЬ: Болен? Оставайся дома

Используйте технологию отслеживания контактов >>, соблюдайте >> рекомендации по социальному дистанцированию и установить систему видеонаблюдения >> чтобы спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таким странам, как США и Китай, чтобы остановить распространение COVID-19, поскольку это заразное заболевание.

---

RF Беспроводные калькуляторы и преобразователи

Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения. Сюда входят такие беспроводные технологии, как GSM, UMTS, LTE, 5G NR и т. Д. СПРАВОЧНЫЕ КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR ➤5G NR ARFCN против преобразования частоты ➤Калькулятор скорости передачи данных LoRa ➤LTE EARFCN для преобразования частоты ➤Калькулятор антенн Яги ➤ Калькулятор времени выборки 5G NR

---

IoT-Интернет вещей Беспроводные технологии

Раздел IoT охватывает беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth Low Power (BLE), NFC, RFID, INSTEON, X10, KNX, ANT +, Wavenis, Dash7, HomePlug и другие.Он также охватывает датчики Интернета вещей, компоненты Интернета вещей и компании Интернета вещей.
См. Главную страницу IoT >> и следующие ссылки.
➤ НИТЬ ➤EnOcean ➤Учебник по LoRa ➤Учебник по SIGFOX ➤WHDI ➤6LoWPAN ➤Zigbee RF4CE ➤NFC ➤Lonworks ➤CEBus ➤UPB

СВЯЗАННЫЕ ЗАПИСИ

RF Wireless Tutorials

Различные типы датчиков

Поделиться страницей

Перевести страницу

Основы индуктивности | EC&M

Индуктивность — это связь между электрическими цепями и магнитными полями.

Синусоидальные волны напряжения и тока синфазны, когда они достигают пика и одновременно пересекают нулевую ось. Однако это случается редко и только в цепях переменного тока (AC), содержащих чистые сопротивления. Большинство цепей переменного тока содержат тот или иной тип индуктивности, и в этом случае форма волны тока отстает от напряжения или достигает своего пика немного позже формы волны напряжения. Запаздывающий ток указывает на индуктивную цепь.

Источники индуктивности. Катушка индуктивности состоит из катушки с проволокой, намотанной на железный или немагнитный (воздушный) сердечник.Ток, проходящий через катушку индуктивности, создает магнитный поток. Результирующее магнитное поле может накапливать энергию, которая передается назад и вперед между электрической цепью и магнитной цепью, создаваемой индуктором. Величина индуктивности измеряется в Генри , количестве магнитного потока, создаваемого каждым ампером тока. Индуктивное реактивное сопротивление — это индуктивность, умноженная на радианную частоту системы.

Многие устройства переменного тока содержат катушки с проводом. Трансформаторы, например, представляют собой две или более катушек изолированного провода, обернутого вокруг железного сердечника.Двигатели обычно имеют статор, неподвижную катушку изолированного провода, которая окружает вторую катушку изолированного провода, которая может свободно вращаться (ротор). Трансформаторы и двигатели широко используются в большинстве энергосистем, что делает большинство систем переменного тока индуктивными по своей природе.

Основы индуктивности.

Ток, протекающий через спиральный провод индуктора, создает магнитное поле, окружающее проводник. Направление магнитного поля находится по правилу правой руки.Большой палец правой руки направьте по направлению тока. Пальцы сгибаются в направлении магнитного поля.

Переменный ток, протекающий через катушку индуктивности, создает изменяющееся во времени магнитное поле. По мере того, как поле увеличивается по величине, в нем накапливается энергия, обеспечиваемая электрической цепью. Когда поле схлопывается, его энергия возвращается в электрическую цепь. Этот цикл увеличения / уменьшения происходит 120 раз в секунду в системе с частотой 60 Гц.

Применение индуктивности.

Катушки индуктивности, часто называемые в силовых приложениях реакторами, используются для изменения характеристик энергосистемы. При последовательном соединении реакторы значительно увеличивают импеданс противофазного тока. Поскольку ток, протекающий во время короткого замыкания, почти на 90 ° не совпадает по фазе с напряжением системы, для ограничения тока короткого замыкания можно использовать последовательные реакторы. Токоограничивающие реакторы могут стать рентабельной альтернативой замене автоматических выключателей, когда величина тока короткого замыкания превышает номинальные параметры оборудования.Подключение реакторов от линии к нейтрали (в шунте) противодействует емкостным эффектам зарядки линии, которые могут вызывать недопустимо высокие напряжения в очень длинных линиях передачи. Шунтирующие реакторы распространены на линиях сверхвысокого напряжения (СВН) протяженностью в сотни миль.

Влияние индуктивности.

По мере увеличения индуктивности в цепи переменного тока увеличивается и величина, на которую ток отстает от напряжения. Величина задержки измеряется в электрических градусах. Косинус числа градусов запаздывания называется коэффициентом мощности (PF) схемы.У чисто резистивной схемы нет запаздывания (0 °). Косинус 0 ° равен 1 или единице. Коэффициент мощности единства — это то, чего вы хотите достичь в силовых цепях.

Индуктивный ток сдвинут по фазе на 90 ° по отношению к резистивному току. Прямоугольный треугольник, называемый треугольником импеданса, может быть образован путем проведения гипотенузы между сопротивлением и индуктивными реактивными величинами. Если индуктивное реактивное сопротивление в цепи составляет 48,4% от сопротивления, можно использовать тригонометрию, чтобы проиллюстрировать, что ток будет отставать от напряжения на 25.8 °. Косинус 25,8 ° равен 0,90, или 90%, поэтому коэффициент мощности схемы отстает на 90% (, рис. выше).

Позже мы обсудим, как приблизить схему коэффициента мощности с запаздыванием на 90% к единице. Хороший коэффициент мощности важен для правильной работы энергосистемы. Когда коэффициент мощности слишком низкий, электрическая система может страдать от плохого регулирования напряжения и чрезмерных потерь.

Фер — технический консультант из Клируотера, Флорида

Реактивное сопротивление | электроника | Britannica

Реактивность в электричестве, мера сопротивления, которое цепь или часть цепи представляет электрическому току, поскольку ток переменный или переменный.Постоянные электрические токи, протекающие по проводникам в одном направлении, испытывают сопротивление, называемое электрическим сопротивлением, но не реактивным сопротивлением. Реактивность присутствует в дополнение к сопротивлению, когда по проводникам протекает переменный ток. Реактивность также возникает в течение коротких интервалов времени, когда постоянный ток изменяется по мере приближения к установившемуся потоку или отклонения от него, например, когда переключатели замкнуты или разомкнуты.

Реактивное сопротивление бывает двух типов: индуктивное и емкостное. Индуктивное реактивное сопротивление связано с магнитным полем, окружающим провод или катушку, по которой проходит ток.Переменный ток в таком проводнике или индукторе создает переменное магнитное поле, которое, в свою очередь, влияет на ток и напряжение (разность потенциалов) в этой части цепи. Катушка индуктивности по существу противодействует изменениям тока, заставляя изменения тока отставать от изменений напряжения. Ток нарастает по мере того, как управляющее напряжение уже уменьшается, имеет тенденцию продолжаться на максимальном значении, когда напряжение меняет свое направление, падает до нуля, когда напряжение увеличивается до максимума в противоположном направлении, и меняет свое направление и нарастает в в том же направлении, что и напряжение, даже когда напряжение снова падает.Индуктивное реактивное сопротивление, мера этого противодействия току, пропорционально как частоте f переменного тока, так и свойству индуктора, называемому индуктивностью (обозначено L и, в свою очередь, зависит от размеров индуктора, его расположения, и окружающая среда). Индуктивное реактивное сопротивление X _L равно 2π умноженному на произведение частоты тока и индуктивности проводника, просто X _L = 2π f L. Индуктивное реактивное сопротивление выражается в омах. (Единица измерения частоты — герцы, индуктивности — Генри.)

С другой стороны, емкостное реактивное сопротивление связано с изменяющимся электрическим полем между двумя проводящими поверхностями (пластинами), отделенными друг от друга изолирующей средой. Такой набор проводников, конденсатор, по существу противодействует изменениям напряжения или разности потенциалов на своих пластинах. Конденсатор в цепи замедляет прохождение тока, заставляя переменное напряжение отставать от переменного тока, в отличие от отношения, вызванного индуктором.Емкостное реактивное сопротивление, мера этого противостояния, обратно пропорционально частоте f переменного тока и свойству конденсатора, называемому емкостью (обозначено C и зависит от размеров конденсатора, его расположения и изоляционной среды. ). Емкостное реактивное сопротивление X _C равно произведению 2π, частоты тока и емкости этой части цепи, просто X _C = 1 / (2 π f C ).Емкостное реактивное сопротивление измеряется в омах. (Единица измерения емкости — фарады.)

Поскольку индуктивное реактивное сопротивление X _L заставляет напряжение опережать ток, а емкостное реактивное сопротивление X _C вызывает отставание напряжения от тока, всего реактивное сопротивление X — это их разница, то есть X = X _L — X _C . Величина, обратная реактивному сопротивлению, 1/ X , называется восприимчивостью и выражается в единицах обратного сопротивления, называемых mho ( Ом, записано наоборот).

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Магнитная индукция, индуктивность, цепи переменного тока и LC

Итак, для чистой индуктивности без потерь VL «опережает» IL на 90o, или мы можем сказать, что IL «отстает» от VL на 90o.

Есть много разных способов запомнить фазовое соотношение между напряжением и током, протекающим через чистую цепь индуктивности, но один очень простой и легко запоминающийся способ — использовать мнемоническое выражение «ELI» (произносится как Элли, как в имя девушки).ELI означает сначала электродвижущую силу в индуктивности переменного тока, L перед током I. Другими словами, напряжение перед током в катушке индуктивности, E, L, I равно «ELI», и в зависимости от того, с какого фазового угла начинается напряжение, это выражение всегда верно для чистой цепи индуктивности.

Влияние частоты на индуктивное сопротивление

Когда источник питания 50 Гц подключен через подходящую индуктивность переменного тока, ток будет задержан на 90o, как описано ранее, и получит пиковое значение I ампер перед напряжение меняет полярность в конце каждого полупериода, т.е.е. ток возрастает до максимального значения за «T сек».

Если мы теперь подадим на катушку источник питания 100 Гц с таким же пиковым напряжением, ток все равно будет задерживаться на 90 °, но его максимальное значение будет ниже, чем значение 50 Гц, потому что время, необходимое для достижения максимального значения, имеет был уменьшен из-за увеличения частоты, потому что теперь у него есть только «1/2 T секунд», чтобы достичь своего пикового значения. Кроме того, скорость изменения потока в катушке также увеличилась из-за увеличения частоты.

Тогда из приведенного выше уравнения для индуктивного реактивного сопротивления можно увидеть, что если либо частота, либо индуктивность увеличиваются, общее значение индуктивного реактивного сопротивления катушки также увеличится. По мере того, как частота увеличивается и приближается к бесконечности, реактивное сопротивление катушек индуктивности и, следовательно, его полное сопротивление также будет увеличиваться в сторону бесконечности, действуя как разомкнутая цепь.

Аналогичным образом, когда частота приближается к нулю или постоянному току, реактивное сопротивление катушек индуктивности также будет уменьшаться до нуля, действуя как короткое замыкание.Это означает, что индуктивное реактивное сопротивление «прямо пропорционально частоте» и имеет небольшое значение на низких частотах и ​​высокое значение на более высоких частотах, как показано.

Индуктивное реактивное сопротивление относительно частоты

Индуктивное реактивное сопротивление катушки индуктивности увеличивается с увеличением частоты на ней, поэтому индуктивное реактивное сопротивление пропорционально частоте (XL α ƒ), так как обратная ЭДС, генерируемая в индуктивность равна его индуктивности, умноженной на скорость изменения тока в катушке индуктивности.

Также по мере увеличения частоты ток, протекающий через катушку индуктивности, также уменьшается.

Мы можем представить влияние очень низких и очень высоких частот на реактивное сопротивление чистой индуктивности переменного тока следующим образом:

В цепи переменного тока, содержащей чистую индуктивность, применяется следующая формула: Итак, как мы пришли к этому уравнению. Самоиндуцированная ЭДС в катушке индуктивности определяется законом Фарадея, который производит эффект самоиндукции в катушке индуктивности из-за скорости изменения тока, и максимальное значение наведенной ЭДС будет соответствовать максимальной скорости изменения.Тогда напряжение в катушке индуктивности определяется как:

, тогда напряжение на индуктивности переменного тока будет определено как:

Где: VL = IωL, амплитуда напряжения и θ = + 90o, которая представляет собой разность фаз или фазовый угол между напряжением и током.

В векторной области

В векторной области напряжение на катушке задается как:

и в полярной форме это будет записано как: XL∠90o, где: Переменный ток через последовательную цепь R + L

Выше мы видели, что ток, протекающий через чисто индуктивную катушку, отстает от напряжения на 90o, и когда мы говорим чисто индуктивную катушку, мы имеем в виду катушку, у которой нет омическое сопротивление и, следовательно, отсутствие потерь I2R.Но в реальном мире невозможно иметь только индуктивность только переменного тока.

Все электрические катушки, реле, соленоиды и трансформаторы будут иметь определенное сопротивление, независимо от того, насколько мало они связаны с используемыми витками катушки. Это связано с тем, что медная проволока обладает удельным сопротивлением. Тогда мы можем рассматривать нашу индуктивную катушку как имеющую сопротивление R, соединенное последовательно с индуктивностью L, создающую то, что можно условно назвать «нечистой индуктивностью».

Если катушка имеет некоторое «внутреннее» сопротивление, тогда нам нужно представить полный импеданс катушки как сопротивление последовательно с индуктивностью и в цепи переменного тока, которая содержит как индуктивность, L, так и сопротивление, R, напряжение, V в комбинации будет векторной суммой двух составляющих напряжений, VR и VL.

Это означает, что ток, протекающий через катушку, по-прежнему будет отставать от напряжения, но на величину менее 90o в зависимости от значений VR и VL, суммы векторов. Новый угол между формами волны напряжения и тока дает нам их разность фаз, которая, как мы знаем, является фазовым углом цепи с греческим символом phi, Φ.

Рассмотрим схему ниже с чистым неиндуктивным сопротивлением, R соединен последовательно с чистой индуктивностью L.

https://www.electronics-tutorials.ws/accircuits/ac-inductance.html

Катушки индуктивности

Введение

Катушки индуктивности

— это простые по конструкции компоненты, состоящие из катушек изолированного медного провода, намотанного вокруг каркаса, который будет иметь какой-либо тип сердечника в центре. Этот сердечник может быть из металла, например железа, который легко намагничивается; или в высокочастотных индукторах, скорее всего, это будет просто воздух.

Действие индукторов зависит от магнитного поля, которое присутствует вокруг любого проводника, когда по нему проходит ток. Если катушка с проволокой намотана вокруг сердечника, сделанного из материала, который легко намагничивается, такого как железо, то магнитное поле вокруг катушки концентрируется внутри сердечника; это значительно увеличивает эффективность индуктора.

Катушки индуктивности в цепях переменного тока.

Катушки индуктивности

широко используются в приложениях переменного тока (AC), таких как радио, телевидение и оборудование связи, и в этих системах очень полезно то, как катушки индуктивности реагируют на сигналы переменного тока различных частот.

Дроссели.

Другое название индуктора — «дроссель». Катушки индуктивности, представляющие собой просто катушки из медной проволоки, позволяют легко проходить постоянному току, но когда применяется переменный ток, индукторы создают сопротивление потоку тока, который увеличивается по мере увеличения частоты переменного тока. Следовательно, переменному току не разрешается течь или он «перекрывается», в то время как постоянный ток может проходить. Этот эффект используется в цепях питания, где сеть переменного тока общего пользования (линия) должна быть преобразована в источник постоянного тока, пригодный для питания электронных схем.

Накопитель энергии в цепи постоянного тока.

Рис. 3.0.1 Обратная ЭДС в индукторе.

Когда на катушку индуктивности подается постоянное напряжение, через нее протекает ток. Поскольку этот ток увеличивается при включении, вокруг катушек с проволокой создается увеличивающееся магнитное поле. Таким образом, электрическая энергия, используемая для создания магнитного поля, сохраняется в виде магнитной энергии. Кроме того, когда энергия в магнитном поле изменяется, это вызывает напряжение в тех же катушках, которые создают магнитное поле.

Однако индуцированное напряжение, называемое «электромагнитной силой самоиндукции», будет иметь полярность, противоположную приложенному напряжению, которое создает магнитное поле; следовательно, это вызвало ЭДС. также обычно называют «обратной ЭДС». и его эффект заключается в замедлении в противном случае быстрого изменения тока, которое имеет место при включении.

По мере того, как ток через катушку индуктивности нарастает, скорость изменения тока уменьшается из-за обратной ЭДС, как и обратная ЭДС из-за уменьшения скорости изменения тока.Электрическая энергия, приложенная к индуктору, теперь преобразована в магнитную энергию и сохраняется в магнитном поле, созданном вокруг индуктора.

Если напряжение, приложенное к индуктору, теперь отключено, энергия, накопленная в магнитном поле, возвращается обратно в катушки индуктора, на этот раз нет противоположного напряжения питания, поэтому все магнитное поле мгновенно схлопывается, и накопленная энергия, теперь в виде напряжения на катушке индуктивности, но с полярностью, противоположной исходному приложенному напряжению.

Однако теперь это напряжение будет намного больше, чем исходное напряжение питания; это потому, что амплитуда напряжения, индуцированного в проводнике, пропорциональна (среди прочего) скорости изменения магнитного поля. При включении из-за изменения двух противоположных напряжений, увеличения подачи и противоэдс. снижаясь, скорость изменения замедлялась. Однако при выключении напряжение питания отсутствует, поэтому магнитное поле очень быстро разрушается, вызывая очень высокую скорость изменения и, следовательно, генерируя очень большой импульс напряжения.

Этот импульс может иметь амплитуду в десятки, сотни или тысячи вольт, что может быть очень полезно, например в возникновении искры зажигания в бензиновом двигателе или очень опасно, например нехорошо на ощупь! Он также может очень легко разрушить другие компоненты, такие как полупроводники, и может стать источником серьезных радиопомех.

Узнать больше о back e.m.f. здесь.

Катушки индуктивности многих типов.

Физические размеры катушек индуктивности сильно различаются в зависимости от потребляемой мощности и частоты используемого переменного тока; от огромных силовых трансформаторов на электростанциях и электросетях до крошечных индукторов в радиооборудовании, состоящих из нескольких витков провода и всего несколько миллиметров в поперечнике.

No related posts.