Формула индукции магнитного поля, B

Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.

Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора равен частному от деления максимальной силы (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():

   

Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:

   

где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и .

Направления , векторов и связаны между собой правилом левой руки.

Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:

   

где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:

   

где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().

Принцип суперпозиции магнитных полей

Если магнитное поле получается в результат наложения нескольких магнитных полей то, магнитная индукция поля (), может быть найдена как векторная сумма магнитных индукций отдельных полей ():

   

Закон Био-Савара-Лапласа, как формула для вычисления величины индукции магнитного поля

Закон Био-Савара – Лапласа является одним из распространенных законов, который позволяет вычислить вектор магнитной индукции () в любой точке магнитного поля, создаваемого в вакууме элементарным проводником с током:

   

где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная.

Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).

Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:

   

где – относительная магнитная проницаемость вещества.

Частные случаи формул для вычисления модуля вектора магнитной индукции

Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):

   

где R – радиус витка.

Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:

   

где r – расстояние от оси проводника до точки, в которой рассматривается поле.

В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:

   

где n – количество витков соленоида на единицу длины; I – сила тока в витке.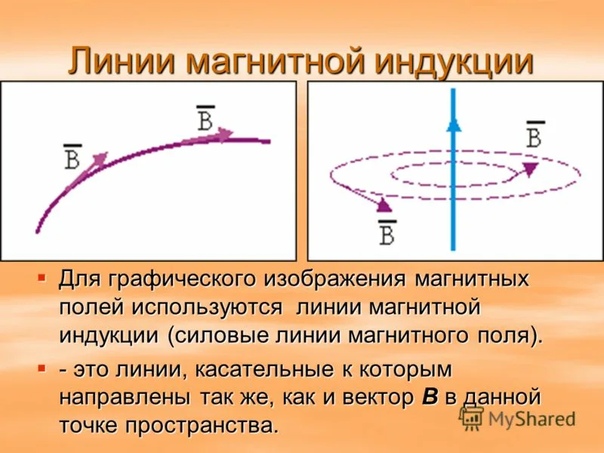

Примеры решения задач по теме «Индукция магнитного поля»

НАЧАЛА ФИЗИКИ

Кроме индукции поля кольца на его оси, существует еще одна задача, для которой индукцию магнитного поля необходимо помнить. Это поле прямого провода с током. Итак, пусть существует бесконечный прямой провод, по которому течет ток I. Тогда этот ток создает магнитное поле, индукция которого на расстоянии r от него, определяется соотношением

(28.8)

Направлен вектор индукции магнитного поля провода по касательным к окружностям, лежащим в плоскостях, перпендикулярных проводу, центр которых совпадает с проводом. Причем если смотреть на эти окружности в направлении тока в проводе, вектор индукции в каждой точке будет направлен по часовой стрелке. Соотношение (28.8) установлено на основе закона Био-Савара-Лапласа и принципа суперпозиции. Но при ее выводе не обойтись без высшей математики. Поэтому вывод соотношения (28.8) не входит в школьный курс физики, и мы также его не приводим.

Формула (28.8) позволяет вычислять индукцию магнитного поля, созданного несколькими прямыми проводами, или <кусочками> прямых проводов. Рассмотрим пример.

Рис. 28.6

Пример 28.3. Определить индукцию магнитного поля в точке О, если проводник с током I представляет собой два параллельных прямых провода и три четверти кольца радиуса R (рис. 28.6). Точка О — центр кольца.

Решение. Согласно принципу суперпозиции каждый элемент тока создает свое собственное поле независимо от других элементов, а результирующее поле есть векторная сумма этих полей. Но при суммировании поля малых элементов провода мы можем просуммировать сначала по элементам одного прямого провода, затем второго, а затем элементам, входящим в состав кусочка кольца. Поэтому индукция магнитного поля нашего провода представляет собой сумму индукций, создаваемых в любой точке двумя прямыми проводами и проводом, представляющим собой три четверти кольца.

433/597

Глава 22.

Магнитные взаимодействия. Магнитная индукция.Силы Лоренца и Ампера

Если заряд движется, то наряду с электрическим полем он создает еще одно поле — магнитное, которое действует на другие движущиеся заряды. В результате возникает дополнительное (наряду с кулоновским) взаимодействие движущихся электрических зарядов, которое называется магнитным. В результате магнитного взаимодействия возникает взаимодействие проводников с током.

В 1820 г. датский физик Х. Эрстед обнаружил, что проводник с током действует на магнитную стрелку. После этого стало ясно, что магнитное взаимодействие движущихся электрических зарядов и токов и взаимодействие постоянных магнитов имеют одну и ту же природу. На основании подробных исследований А. Ампер установил, что взаимодействие постоянных магнитов между собой и с токами можно объяснить, если предположить, что внутри магнитов есть электрические токи (в настоящее время известно, что эти токи имеют внутримолекулярную природу).

Для характеристики магнитного поля вводится векторная величина, которая называется индукцией магнитного поля и которая позволяет найти силы, действующие со стороны магнитного поля на движущиеся заряды. Как правило, эту величину обозначают буквой . Для нахождения индукции в каждой точке магнитного поля, созданного проводником с током, используется закон Био-Савара-Лапласа и принцип суперпозиции. Закон Био-Савара-Лапласа позволяет найти поле , созданное бесконечно малым элементом проводника, а принцип суперпозиции требует сложить векторы индукции, созданные всеми элементами проводников. Закон Био-Савара-Лапласа в школьный курс физики, однако, не входит. В задачи ЕГЭ входят только вопросы, связанные с направлением вектора магнитной индукции (но не с величиной). Существует несколько вариантов правила нахождения направления вектора . Наиболее удобным является правило буравчика — оно более универсально, чем правило левой руки. Правило буравчика утверждает, что если вкручивать

правыйбуравчик¹ по току в проводнике, то направление движения ручки в каждой точке пространства покажет направление вектора индукции магнитного поля в этой точке. Относительно величины достаточно помнить, что чем дальше от проводника, тем меньше индукция, и что внутри бесконечной катушки (бесконечного соленоида) магнитное поле направлено вдоль оси катушки и однородно.

Магнитное поле можно изобразить графически с помощью линий магнитной индукции. Линии магнитной индукции — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этой точке. Линии магнитной индукции проводят так, что их густота в каждой области пространства пропорциональна величине индукции в этой области. В отличие от силовых линий электрического поля линии магнитной индукции всегда являются замкнутыми.

На электрический заряд величиной , движущийся со скоростью в магнитном поле с индукцией , со стороны магнитного поля действует сила, которая называется силой Лоренца

(22.1)

где — угол между скоростью и вектором индукции. Направление силы Лоренца определяется следующим образом (см. рисунок).

1. Сила Лоренца перпендикулярна плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля (на рисунке эта плоскость показана тонким пунктиром).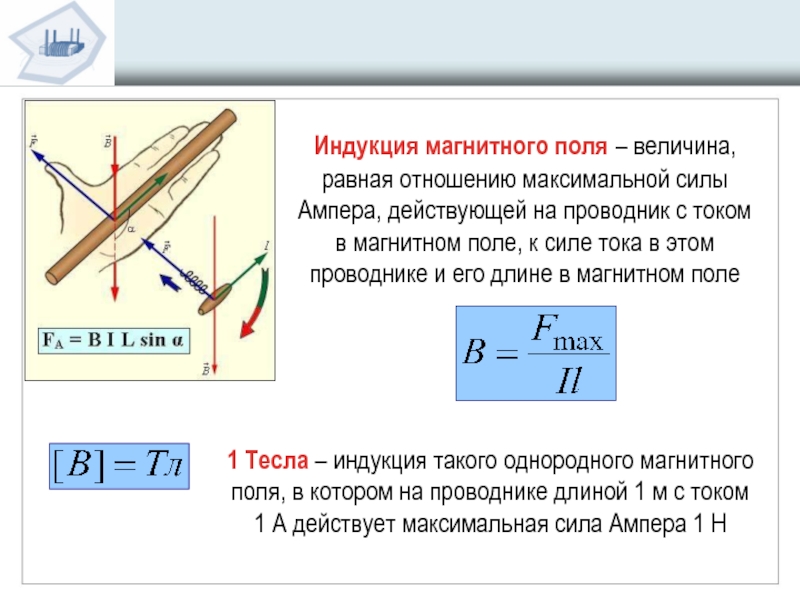

2. Выбор между двумя перпендикулярными направлениями осуществляется с помощью правила буравчика (или правила левой руки): если вращать правый буравчик так, что его ручка движется от вектора к вектору , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд (траектория ручки буравчика показана на рисунке изогнутой стрелкой).

3. Для отрицательного заряда направление силы Лоренца противоположно.

Можно также определять направление силы Лоренца по правилу левой руки: левую руку нужно расположить так, чтобы вектор входил в ладонь, направление четырех пальцев совпадало с направлением вектора скорости заряда, тогда направление отогнутого под прямым углом к четырем пальцам большого пальца покажет направление силы, действующей на положительный заряд (на отрицательный заряд действует сила противоположного направления).

Поскольку магнитное поле действует на движущиеся заряды, то магнитное поле действует и на проводник, по которому течет электрический ток. Если в магнитном поле с индукцией находится проводник длиной , по которому течет ток , то на этот проводник действует сила

(22.2)

где — угол между током и вектором индукции. Направлен вектор силы (22.2) перпендикулярно плоскости, в которой лежат вектор и проводник, причем в таком направлении, что если поставить правый буравчик перпендикулярно указанной плоскости и вращать его так, что ручка вращается от тока к вектору , то направление его вкручивания покажет направление силы (см. рисунок; плоскость в которой лежат проводник и вектор индукции обозначена тонким пунктиром, движение ручки буравчика — изогнутой стрелкой). Также для нахождения направления силы можно использовать правило левой руки. Сила (22.2), действующая со стороны магнитного поля на проводник с током, называется силой Ампера.

Рассмотрим теперь задачи.

Правильный ответ в задаче 22.1. 1 — 4 (магнитное поле создается движущимися заряженными телами), в задаче 22.1.2 — 2 (в магнитном веществе есть незатухающие электрические токи). Что же касается того, заряжен магнит или нет, то от этого существование магнитного поля (если магнит покоится) не зависит.

В задаче 22.1.3 следует воспользоваться правилом буравчика. Если вкручивать буравчик по направлению тока в проводнике, то в точке его ручка будет двигаться за чертеж. Следовательно, за чертеж направлен в точке и вектор индукции магнитного поля (ответ 1).

Если вкручивать буравчик по току в кольце (в любой точке кольца), то ручка буравчика в центре кольца будет двигаться за чертеж. Поэтому правильный ответ в задаче 22.1.4 — 3.

Поскольку угол между скоростью заряда и вектором магнитной индукции равен нулю (задача 22.1.5), то согласно формуле (22.1) сила Лоренца, действующая на этот заряд, равна нулю (ответ 4).

Применим к проводнику с током из задачи 22.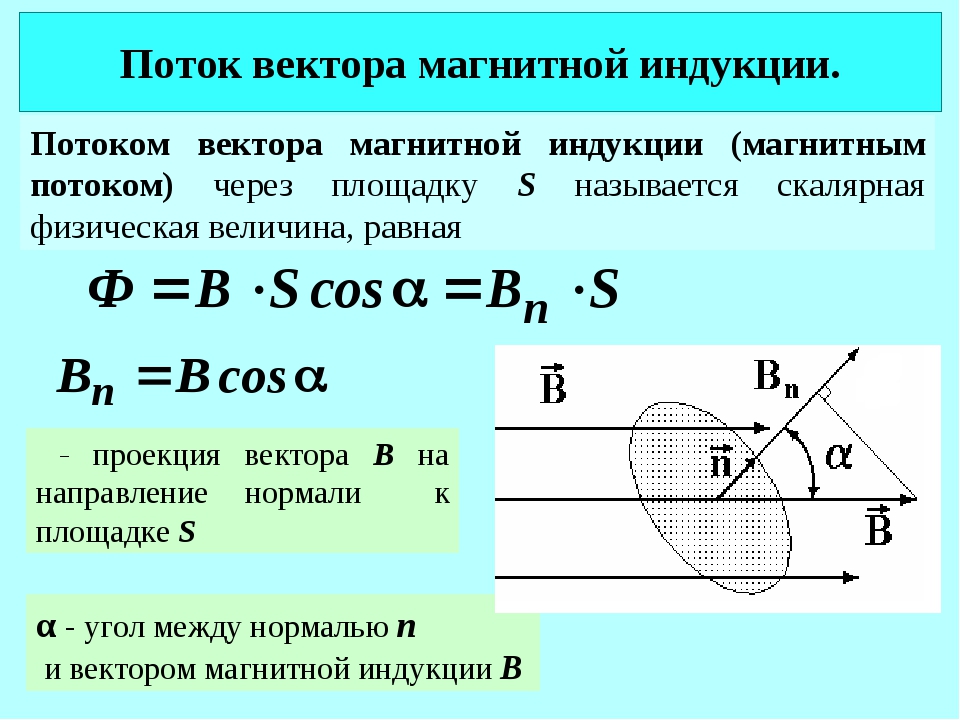 1.6 формулу (22.2) для силы Ампера. Имеем (ответ 2).

Как следует из формулы (22.2) сила Ампера равна нулю, если угол между током и индукцией равен нулю или 180°. Из приведенных на рисунке в задаче 22.1.7 проводников, таковым является только проводник 1. Поэтому на него магнитное поле не действует (ответ 1).

Применяем к частице из задачи 22.1.8 (см. рисунок) правила нахождения направления силы Лоренца (пункты 1-3 после формулы (22.1)). Во-первых, сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля — т.е. либо за чертеж, либо на нас. Во-вторых, при вращении ручки буравчика, поставленного на чертеж в ту точку, где находится заряд, от вектора к вектору (в направлении меньшего угла между ними), буравчик будет «выкручиваться» из чертежа. А по-скольку частица заряжена положительно, сила Лоренца направлена «на нас» (ответ 1).

Используя правила для силы Ампера (формула (22. 2) и текст после нее), найдем, что сила Ампера, действующая со стороны магнитного поля на проводник с током в задаче 22.1.9, направлена «от нас» (ответ 3).

В задаче 22.1.10 следует сначала найти направление вектора магнитной индукции поля провода в той точке, где находится заряд, а затем использовать правила для силы Лоренца (формула (22.1) и текст за ней). Согласно результатам задачи 22.1.3, вектор в той точке, где находится заряд, направлен за чертеж (см. рисунок).

Вектор силы Лоренца направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. либо к проводу, либо от него. Ставим буравчик перпендикулярно этой плоскости и вращаем его так, что ручка движется от вектора к вектору (см. рисунок; буравчик нужно вращать по часовой стрелке, если смотреть снизу). При таком вращении буравчик будет вкручиваться вверх. А поскольку электрон заряжен отрицательно, то действующая на него сила направлена противоположно, т. е. от провода (ответ 2).

В задаче 22.2.1 используем принцип суперпозиции. Ток в горизонтальном кольце создает поле в его центре с индукцией, направленной вверх, ток в вертикальном кольце — с индукцией, направленной вправо (см. задачу 22.1.4.). Результат сложения этих векторов — индукция суммарного магнитного поля — направлена на «северо-восток» (ответ 1).

Ток в верхнем проводе (задача 22.2.2) создает поле с индукцией, направленной «за чертеж», ток в нижнем — «на нас». Результат их сложения зависит от величин этих векторов. Поскольку поле нижнего провода в точке больше поля верхнего (меньше расстояние), то вектор суммы направлен «на нас» (ответ 1).

Сила Лоренца в любой момент времени перпендикулярна скорости частицы. Поэтому угол между бесконечно малым перемещением частицы в любой момент времени и силой Лоренца, действующей на частицу в этот момент времени, — прямой. А поскольку в формулу для работы силы на бесконечно малом участке перемещения входит косинус угла между силой и перемещением, то работа силы Лоренца равна нулю (задача 22. 2.3 — ответ 3). Из этих рассуждений и теоремы об изменении кинетической энергии следует, что заряженная частица, движущаяся под действием магнитного поля, изменяет направление, но не величину своей скорости.

Если заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, то она движется по окружности, причем эта окружность лежит в плоскости, перпендикулярной линиям магнитной индукции. Радиус окружности можно найти из второго закона Ньютона для этой частицы

(22.3)

где и — масса частицы и ее заряд, — ускорение, — скорость, которая не изменяется по величине (см. предыдущую задачу), — индукция магнитного поля. В формуле (22.3) использовано известное выражение для центростремительного ускорения . Из формулы (22.3) получаем для радиуса окружности

(22. 4)

Применяя формулу (22.4) к задаче 22.2.4 находим отношение радиусов окружности первой и второй частиц

(ответ 2).

Найдем сначала скорости протона и -частицы, ускоренных одним и тем же напряжением (задача 22.2.5). По теореме об изменении кинетической энергии имеем

где и — масса частицы и ее заряд, — скорость, которую частица приобретает после разгона (здесь предполагается, что начальная скорость частицы равна нулю). Из этой формулы находим отношение скоростей протона и -частицы , ускоренных одним и тем же напряжением

Поскольку заряд протона вдвое меньше заряда -частицы, а масса вчетверо меньше, то . Теперь из формулы (22.4) находим отношение радиусов окружности протона и  -частицы, ускоренных одним и тем же электрическим напряжением и движущихся в одном и том же магнитном поле

(ответ 4).

Период обращения заряженной частицы в магнитном поле (задача 22.2.6) можно найти из следующих соображений. В однородном магнитном поле частица движется по окружности и за период проходит путь, равный длине этой окружности , где — ее радиус. Используя формулу (22.4) для радиуса траектории, получим для периода обращения

где — скорость частицы, — ее масса, — заряд, — индукция магнитного поля. Отсюда заключаем, что период обращения заряженной частицы в магнитном поле не зависит от ее скорости (ответ 3).

Индукция магнитного поля в задаче 22.2.7 должна быть направлена так, чтобы сила Лоренца, действующая на электрон, была направлена к центру окружности, по которой он движется (см. рисунок). А поскольку сила Лоренца перпендикулярна скорости и индукции, то вектор индукции может быть направлен в этой ситуации только «за чертеж» или «на нас». Воспользуемся далее правилом буравчика (см. текст после формулы (22.1)): если вращать буравчик так, что его ручка будет вращаться от скорости заряда к индукции магнитного поля , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд. Для электрона ( < 0) направление силы противоположно. Непосредственной проверкой убеждаемся, что вектор индукции направлен «за чертеж» (ответ 4).

В области среднего провода (задача 22.2.8) ток в верхнем проводе создает магнитное поле с индукцией, направленной «от нас», ток в нижнем — «на нас» (см. задачу 22.1.3). Но ток в нижнем проводе вдвое меньше тока в верхнем, а индукция поля — пропорциональна току. Поэтому индукция суммарного поля верхнего и нижнего проводов в области среднего провода направлена «от нас». Согласно правилам нахождения направления силы Ампера (см. текст после формулы (22.2)) находим, что сила, действующая на средний провод со стороны магнитного поля верхнего и нижнего проводов, направлена вверх (ответ 1). Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.

В задаче 22.2.9 магнитное поле действует на рамку следующим образом. На стороны и , которые параллельны линиям индукции, поле не действует. На стороны и действуют силы Ампера, равные по величине , где — ток в рамке, — индукция магнитного поля, — длина стороны. Сила, действующая на сторону , направлена «на нас», на сторону — «от нас». Поскольку суммарная сила, действующая на рамку, равна нулю, как целое рамка перемещаться в пространстве не будет, а будет вращаться вокруг оси, показанной на рисунке пунктиром (ответ 4).

Задача 22.2.10 по формуле (22.2) находим силы Ампера, действующие на стороны треугольника

где — ток в контуре, и — длины сторон и , — индукция магнитного поля (последняя из приведенных формул следует из того, что сторона параллельна линиям индукции). Из теоремы синусов для треугольника

заключаем, что , а из правил для направления силы Ампера — что один из векторов или направлен «за чертеж», один — «на нас» (в зависимости от направления тока в контуре). Поэтому правильный ответ в задаче — 3.

формула, от чего зависит, линии индукции

 

Все мы знаем, что есть магниты более сильные и менее сильные. Маленький магнитик сможет притянуть пару гвоздей и все, а гораздо более мощный электромагнит домофона удерживает дверь в подъезд так, что несколько взрослых мужчин не смогут открыть ее силой.

Величина, характеризующая величину силы магнита

То есть, мы можем говорить о некой величине, характеризующей величину силы магнитов, а точнее, магнитного поля, создаваемого ими. Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля или магнитной индукции. (см. подробнее электромагнитная индукция)

Обозначается индукция буквой B. Магнитная индукция это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле:

B=F / (I*l)

Или в виде определения:

Модуль вектора магнитной индукции B равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l.

От чего зависит магнитная индукция

Магнитная индукция не зависит ни от силы тока, ни от длины проводника, она зависит только от магнитного поля. То есть, если мы, например, уменьшим силу тока в проводнике, не меняя больше ничего, то уменьшится не индукция, с которой сила тока связана прямо пропорционально, а сила воздействия магнитного поля на проводник. Величина же индукции останется постоянной. В связи с этим индукцию можно считать количественной характеристикой магнитного поля.

Измеряется магнитная индукция в теслах (1 Тл). При этом 1 Тл=1 Н/(А*м) .

Линии индукции магнитного поля

Магнитная индукция имеет направление. Графически ее можно зарисовывать в виде линий. Линии индукции магнитного поля это и есть то, что мы до сих пор в более ранних темах называли магнитными линиями или линиями магнитного поля. Так как мы выше вывели определение магнитной индукции, то мы можем дать определение и линиям магнитной индукции:

Линии магнитной индукции это линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.

В однородном магнитном поле линии магнитной индукции параллельны, и вектор магнитной индукции будет направлен так же во всех точках.

В случае неоднородного магнитного поля, например, поля вокруг проводника с током, вектор магнитной индукции будет меняться в каждой точке пространства вокруг проводника, а касательные к этому вектору создадут концентрические окружности вокруг проводника. Так и будут выглядеть линии индукции магнитного поля расширяющиеся окружности вокруг проводника.

Нужна помощь в учебе?

Предыдущая тема: Обнаружение магнитного поля по его действию на электрический ток
Следующая тема:&nbsp&nbsp&nbspМагнитный поток: определение, направление и количество + пример

Магнитное поле, силовые линии, вектор магнитной индукции, принцип суперпозиции. Курсы по физике

Тестирование онлайн

• Магнитное поле. Основные понятия

• Магнитное поле. Вектор магнитной индукции

Магнитное поле

Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов.

Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваются наэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем.

Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.

Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).

Магнитное поле можно сделать «видимым» с помощью железных опилок.

Магнитное поле проводника с током

А теперь о том, что обнаружили Ханс Кристиан Эрстед и Андре Мари Ампер в 1820 г. Оказывается, магнитное поле существует не только вокруг магнита, но и любого проводника с током. Любой провод, например, шнур от лампы, по которому протекает электрический ток, является магнитом! Провод с током взаимодействует с магнитом (попробуйте поднести к нему компас), два провода с током взаимодействуют друг с другом.

Силовые линии магнитного поля прямого тока — это окружности вокруг проводника.

Направление вектора магнитной индукции

Направление магнитного поля в данной точке можно определить как направление, которое указывает северный полюс стрелки компаса, помещенного в эту точку.

Направление линий магнитной индукции зависит от направления тока в проводнике.

Определяется направление вектора индукции по правилу буравчика или правилу правой руки.

Вектор магнитной индукции

Это векторная величина, характеризующая силовое действие поля.

Индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии r от него:

Индукция магнитного поля в центре тонкого кругового витка радиуса r:

Индукция магнитного поля соленоида (катушка, витки которой последовательно обходятся током в одном направлении):

Принцип суперпозиции

Если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция — векторная сумма индукций каждого из полей в отдельности

Земля является не только большим отрицательным зарядом и источником электрического поля, но в то же время магнитное поле нашей планеты подобно полю прямого магнита гигантских размеров.

Географический юг находится недалеко от магнитного севера, а географический север приближен к магнитному югу. Если компас разместить в магнитном поле Земли, то его северная стрелка ориентируется вдоль линий магнитной индукции в направлении южного магнитного полюса, то есть укажет нам, где располагается географический север.

Характерные элементы земного магнетизма весьма медленно изменяются с течением времени — вековые изменения. Однако время от времени происходят магнитные бури, когда в течение нескольких часов магнитное поле Земли сильно искажается, а затем постепенно возвращается к прежним значениям. Такое резкое изменение влияет на самочувствие людей.

Магнитное поле Земли является «щитом», прикрывающего нашу планету от частиц, проникающих из космоса («солнечного ветра»). Вблизи магнитных полюсов потоки частиц подходят гораздо ближе к поверхности Земли. При мощных солнечных вспышках магнитосфера деформируется, и эти частицы могут переходить в верхние слои атмосферы, где сталкиваются с молекулами газа, образуются полярные сияния.

Частицы диоксида железа на магнитной пленке хорошо намагничиваются в процессе записи.

Поезда на магнитной подушке скользят над поверхностью совершенно без трения. Поезд способен развивать скорость до 650 км/ч.

Работа головного мозга, пульсация сердца сопровождается электрическими импульсами. При этом в органах возникает слабое магнитное поле.

Репетитор-онлайн — подготовка к ЦТ

Пример 2. Длинный прямой проводник находится в воздухе и расположен перпендикулярно линиям индукции однородного магнитного поля, величина которой равна 18 мкТл. По проводнику протекает ток силой 2,4 А. Найти максимальное значение результирующего магнитного поля на расстоянии 1,0 см от проводника.

Решение. На рисунке показано расположение проводника с током в однородном магнитном поле. Силовые линии магнитного поля, созданного током, протекающим по проводнику, представляют собой концентрические окружности, центр которых лежит на указанном проводнике. Заданной точке пространства, в которой определяется результирующее поле, соответствует окружность радиусом r ₀ = 1,0 см.

Величина индукции магнитного поля, образованного током в проводнике, определяется формулой

B′=μ0μI2πr0,

где µ₀ — магнитная постоянная, µ₀ = 4π ⋅ 10⁻⁷ Гн/м; µ — магнитная проницаемость воздуха, µ = 1; I — сила тока в проводнике, I = 2,4 А; r ₀ — расстояние от проводника до той точки, в которой определяется магнитное поле.

Направление магнитного поля, созданного током, определяется по правилу правого винта:

• для точки А — «от нас», т.е. вектор магнитной индукции B′→ имеет такое же направление, как и вектор индукции однородного магнитного поля B→0: B′→↑↑B→0;
• для точки B — «к нам», т.е. вектор магнитной индукции B′→ имеет направление, противоположное направлению вектора индукции однородного магнитного поля B→0: B→′↑↓B→0.

Согласно принципу суперпозиции, для вектора индукции результирующего магнитного поля

B→=B′→+B→0,

или в проекции на координатную ось, направленную в сторону вектора B→0:

• для точки А —

B = B ₀ + B′,

где B ₀ — модуль вектора индукции однородного поля, B ₀ = 18 мкТл;

B = B ₀ − B′.

Сравнение записанных выражений позволяет заключить, что максимальное значение вектора индукции результирующего поля имеет место для точки А и определяется формулой

Bmax=B0+μ0μI2πr0.

Вычисление дает результат:

Bmax=18⋅10−6+4π⋅10−7⋅1⋅2,42π⋅1,0⋅10−2=66⋅10−6 Тл=66 мкТл.

Вектор индукции магнитного поля

Определение

Силовой характеристикой магнитного поля является вектор магнитной индукции $\overrightarrow{B}$. Вектор магнитной индукции является основной характеристикой магнитного поля. Он равен пределу отношения силы, с которой магнитное поле действует на элементарный ток ($Idl$) к произведению тока $(I)$ и величины элемента проводника ($dl$):

Вектор индукции направлен перпендикулярно направлению элементарного тока (или чаще говорят элементу проводника ($\overrightarrow{dl}$)) из (1) и перпендикулярен направлению силы, которая действует со стороны магнитного поля.

Если $\overrightarrow{B}$=const, то магнитное поле называют однородным. Если магнитное поле неизменно во времени, то его называют постоянным.

Иногда модуль вектора индукции однородного магнитного поля определяют как:

где $M_{max}$ — максимальный вращающий момент, действующий на контур с током, который помещен в магнитное поле, $p_m=IS$ — магнитный момент контура ($S$- площадь контура). За направление вектора $\overrightarrow{B}$ принимают направление, в котором устанавливается под действием поля положительная нормаль к контуру с током. Или иначе, говорят, что вектор магнитной индукции направлен в сторону поступательного перемещения правого винта, если его вращать по направлению течения тока в контуре.

Помощь со студенческой работой на тему

Вектор индукции магнитного поля

Очень часто, определение для вектора магнитной индукции записывают в виде:

где $\overrightarrow{dF}$ — сила, действующая на элемент с током. В том случае, если проводник прямолинейный и магнитная индукция во всех точках постоянна, то формулу (2) можно преобразовать в выражение:

Рис. 1

Модуль вектора индукции можно определить, так же исходя из силы Лоренца ($\overrightarrow{F}$), которая действует на движущуюся, со скоростью $\overrightarrow{v}$ заряженную частицу (заряд q) в магнитном поле:

Основной единицей измерения магнитной индукции в системе СИ является тесла (Тл).

Принцип суперпозиции вектора индукции магнитного поля

Эмпирический доказано, что для магнитного поля выполняется принцип суперпозиции:

Если магнитное поле порождается несколькими токами (движущимися зарядами), то оно равно векторной сумме отдельных полей:

Пример 1

Задание: Проводник имеет форму квадрата, сторона которого равна d, по нему течет ток силы I. Найдите магнитную индукцию поля в точке пересечения диагоналей квадрата.

Решение:

Допустим, что плоскость проводника совпадает с плоскостью рис.2. Зададим направление токов.

Рис. 2

В точке О магнитное поле создают четыре прямолинейные проводника с током. Напряженности всех четырех полей направлены в соответствии с правилом правого винта от нас, перпендикулярно плоскости рисунка. Следовательно, векторную сумму полей в принципе суперпозиции заменим на алгебраическую, запишем:

\[B=B_1+B_2+B_3+B_4\left(1.1\right).\]

Причем из симметрии, очевидно, что модули всех индукций равны, значит, запишем, что:

\[B=4B_1\left(1.2\right).\]

В разделе «Электромагнетизм» мы нашли, формулу для расчета модуля вектора магнитной индукции прямолинейного проводника с током. В применении к нашему случаю модуль $\overrightarrow{B}$ будет иметь вид:

\[B_1=\frac{{\mu }_0I}{4\pi b}\left(cos\alpha -cos\beta \right)\left(1.3\right),\]

углы $\alpha $ и $\beta $ указаны на рис.1. В (1.3) $\beta =\pi -\alpha \to cos\beta ={cos \left(\pi -\alpha \right)\ }=-cos\alpha .$ Перепишем (1.3):

\[B_1=\frac{{\mu }_0I}{2\pi b}cos\alpha \left(1.4\right).\]

Так как мы имеем дело с квадратом, то заметим, что: $b=\frac{d}{2},\alpha =\frac{\pi }{4}\to cos\alpha =\frac{\sqrt{2}}{2}.$ Подставим в (1.4), то что мы получили и (1.4) подставим в (1.2), имеем:

\[B=4\cdot \frac{{\mu }_0I}{\pi d}\cdot \frac{\sqrt{2}}{2}=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.\]

Ответ: $B=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.$

Пример 2

Задание: Бесконечно длинный проводник с током (I) согнут под прямым углом (рис.2). Найдите магнитную индукцию поля в точке А, которая указана на рис. 3.

Рис. 3

Решение:

В точке А поле создается двумя частями проводника:

\[\overrightarrow{B}=\overrightarrow{B_{II}}+\overrightarrow{B_{\bot }}\left(2.1\right).\]

Рассмотрим горизонтальный участок, на продолжении которого лежит точка А.3}}\left(2.2\right),\]

где $\overrightarrow{r}$ — радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$).

Индукция магнитного поля бесконечного прямолинейного проводника с током (I) в точке А была бы равна:

\[B’=\frac{{\mu }_0}{2\pi }\frac{I}{b}\left(2.3\right).\]

У нас полу бесконечный проводник, следовательно, из принципа суперпозиции получим, что для нашего проводника индукция равна:

\[{B=B}_{\bot }=\frac{1}{2}B’=\frac{{\mu }_0}{\pi }\frac{I}{b}.\]

Ответ: $B=\frac{{\mu }_0}{\pi }\frac{I}{b}.$

Магнитная индукция в точке O для провода класса 12 по физике CBSE

Подсказка: Данный рисунок разделен на три сегмента, которые содержат два прямых токоведущих провода и один полукруглый токоведущий провод. Чистое магнитное поле в точке $ O $ представляет собой сумму магнитной индукции в этой точке из-за двух токоведущих прямых проводов и магнитной индукции в этой точке из-за полукруглого токоведущего провода. Трехмерное изображение установки визуализируется, чтобы легко решить проблему.

Используемая формула:
$ 1) \ overrightarrow {{{B} _ {ST}}} = \ dfrac {{{\ mu} _ {0}} I} {4 \ pi r} \ widehat {n} $
$ 2) \ overrightarrow {{{B} _ {SC}}} = \ dfrac {{{\ mu} _ {0}} I} {4r} \ widehat {m} $

Полный шаг за шагом ответ:
Для начала изучим данный рисунок. Нам дают провод, по которому течет ток $ I $, расположенный по особой схеме. Нам необходимо найти индукцию магнитного поля в точке $ O $, как показано на рисунке. Для этого представим себе трехмерную картину установки.Также разделим провод на отрезки для удобства расчетов.

Четко наблюдая за приведенным выше рисунком, мы можем понять, что провод разделен на три сегмента. Первый отрезок провода — это $ AB $, который представляет собой не что иное, как прямой провод с током. Второй сегмент провода обозначается как $ BCD $ и представляет собой не что иное, как полукруглый провод с током радиуса $ R $. Третий сегмент провода представлен как $ DE $, который снова является прямым проводом с током.Теперь ясно, что все эти сегменты с тремя токами будут влиять на точку $ O $ из-за магнитной индукции. Чтобы определить полное магнитное поле в этой точке, мы должны отдельно сложить магнитные поля, генерируемые в этой точке из-за всех трех сегментов. Если $ \ overrightarrow {B} $ — полное или чистое магнитное поле в точке $ O $, оно определяется как
$ \ overrightarrow {B} = \ overrightarrow {{{B} _ {AB}}} + \ overrightarrow {{{B} _ {BCD}}} + \ overrightarrow {{{B} _ {DE}}} $
, где
$ \ overrightarrow {{{B} _ {AB}}} $ — индукция магнитного поля при точка $ O $, из-за прямого отрезка $ AB $
$ \ overrightarrow {{{B} _ {BCD}}} $ — индукция магнитного поля в точке $ O $ из-за полукруглого отрезка $ BCD $
$ \ overrightarrow {{{B} _ {DE}}} $ — индукция магнитного поля в точке $ O $ из-за прямого участка $ DE $
Пусть это будет уравнение 1.
Теперь давайте определим каждую из этих индукций магнитного поля отдельно.
Из закона Био-Савара мы знаем, что индукция магнитного поля из-за прямого проводника с током в точке вне проводника определяется выражением
$ \ overrightarrow {{{B} _ {ST}}} = \ dfrac {{{ \ mu} _ {0}} I} {4 \ pi r} \ widehat {n} $
, где
$ \ overrightarrow {{{B} _ {ST}}} $ — индукция магнитного поля за счет прямого тока. -проводящий проводник в точке вне проводника
$ I $ — ток, текущий через проводник
$ {{\ mu} _ {0}} $ — диэлектрическая проницаемость свободного пространства
$ r $ — перпендикулярное расстояние между точкой а проводник
$ \ widehat {n} $ — это направление магнитного поля в этой точке
Пусть это будет уравнение 2.
Из закона Био-Савара мы также знаем, что индукция магнитного поля в центре полукруглого проводника с током равна
$ \ overrightarrow {{{B} _ {SC}}} = \ dfrac {{{\ mu} _ {0}} I} {4r} \ widehat {m} $
, где
$ \ overrightarrow {{{B} _ {SC}}} $ — индукция магнитного поля в центре полукруглого тока. -проводник
$ I $ — ток, текущий по проводнику
$ {{\ mu} _ {0}} $ — диэлектрическая проницаемость свободного пространства
$ r $ — радиус полукруглой дуги
$ \ widehat {m} $ — направление магнитного поля в центре полукруглого сегмента
. Пусть это будет уравнение 3.
Теперь мы можем использовать уравнение 1, чтобы вывести индукции магнитного поля в точке $ O $ из-за сегментов $ AB $, а также $ DE $, потому что оба они являются прямыми проводниками с током, с перпендикулярным расстоянием от $ O $, равным к радиусу полукруглой дуги, как показано на диаграмме.
Кроме того, мы можем использовать уравнение 3 для вывода индукции магнитного поля в точке $ O $ из-за полукруглого сегмента $ BCD $, поскольку точка $ O $ является центром полукруглой дуги, радиус которой задается как $ R $.
Следовательно, используя уравнение 2, мы имеем
$ \ begin {align}
& \ overrightarrow {{{B} _ {AB}}} = \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} (- \ widehat {k}) \\
& \ overrightarrow {{{B} _ {DE}}} = \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} (- \ widehat {k}) \\
\ end {align} $
, где
$ \ overrightarrow {{{B} _ {AB}}} $ — индукция магнитного поля в точке $ O $ из-за прямой отрезок $ AB $ провода
$ \ overrightarrow {{{B} _ {DE}}} $ — индукция магнитного поля в точке $ O $, из-за того, что прямой отрезок $ DE $ провода
$ I $ составляет ток, протекающий через оба этих сегмента провода
$ {{\ mu} _ {0}} $ — диэлектрическая проницаемость свободного пространства
$ R $ — перпендикулярное расстояние между точкой и обоими этими сегментами провода
$ (- \ widehat {k}) $ — направление магнитного поля в точке $ O $, обусловленное обоими этими сегментами провода
. Обозначим эту систему уравнений X.

Аналогично, используя уравнение 3, мы имеем
$ \ overrightarrow {{{B} _ {BCD}}} = \ dfrac {{{\ mu} _ {0}} I} {4R} (- \ widehat {i }) $
, где
$ \ overrightarrow {{{B} _ {BCD}}} $ — индукция магнитного поля в точке $ O $, из-за полукруглого сегмента $ BCD $
$ I $ — текущий текущий через этот отрезок провода
$ {{\ mu} _ {0}} $ — диэлектрическая проницаемость свободного пространства
$ R $ — радиус полукруглой дуги (отрезка) провода
$ (- \ widehat {i }) $ — направление магнитного поля в точке $ O $, обусловленное сегментом $ BCD $ провода
. Пусть это будет уравнение 4.

Подставляя систему уравнений в X и уравнение 4 в уравнение 1, мы получаем
$ \ overrightarrow {B} = \ overrightarrow {{{B} _ {AB}}} + \ overrightarrow {{{B} _ {BCD }}} + \ overrightarrow {{{B} _ {DE}}} = \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} (- \ widehat {k}) + \ dfrac {{{\ mu} _ {0}} I} {4R} (- \ widehat {i}) + \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} (- \ widehat {k}) = \ dfrac {2 {{\ mu} _ {0}} I} {4 \ pi R} (- \ widehat {k}) + \ dfrac {{{\ mu} _ {0}} I } {4R} (- \ widehat {i}) $
, где
$ \ overrightarrow {B} $ — полное или чистое магнитное поле в точке $ O $
Ясно, что величина чистого магнитного поля в точке $ O $ равна от
$ \ осталось | \ overrightarrow {B} \ right | = \ left | \ dfrac {2 {{\ mu} _ {0}} I} {4 \ pi R} (- \ widehat {k}) + \ dfrac {{{\ mu} _ {0}} I} {4R} ( — \ widehat {i}) \ right | = \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} \ sqrt {{{\ pi} ^ {2}} + {{2} ^ {2}}} = \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} \ sqrt {{{\ pi} ^ {2}} + 4} $
Следовательно, магнитное поле индукция в точке $ O $ за счет провода, указанного на рисунке, равна $ \ dfrac {{{\ mu} _ {0}} I} {4 \ pi R} \ sqrt {{{\ pi} ^ {2} } +4} $.Следовательно, правильный ответ — вариант $ C $.

Примечание:
Направление магнитного поля, создаваемого токопроводящим проводником, определяется правилом для большого пальца правой руки. В нашем решении мы учли, что прямые сегменты провода находятся в плоскости $ XY $, а полукруглый сегмент провода находится в плоскости $ ZY $, как показано на приведенном выше рисунке. Используя правило большого пальца правой руки, студенты могут легко вывести направление магнитного поля в точке $ O $, поскольку оба сегмента $ AB $ и $ DE $ находятся в отрицательном направлении оси z $ (- \ widehat {k}) $, как показано.Точно так же они могут сделать вывод, что направление магнитного поля в точке $ O $ из-за сегмента $ BCD $ находится в отрицательном x-направлении $ (- \ widehat {i}) $, как показано. Поскольку нас не просят найти направление полного магнитного поля в точке $ O $ из-за всех трех сегментов, нам достаточно вычислить величину чистого магнитного поля, как это было сделано выше.

Поле магнитной индукции — обзор

4.14 Парамагнитные и ферромагнитные материалы

В парамагнитном материале атомы содержат постоянные магнитные дипольные моменты, возникающие из спина и орбитального углового момента электронов.К кристаллу прикладывается внешнее магнитное поле с индукцией B, где магнитная восприимчивость χm — это константа пропорциональности между вектором намагниченности M (объемной плотностью магнитных диполей) и напряженностью магнитного поля H, так что

(4,182) M = χmH

Эта линейная зависимость от χm применима только к линейным магнитным материалам. В вакууме χm = 0, а в немагнитных материалах он обычно очень мал, в диапазоне от 10-4 до 10-5; например, χm = −0,94 × 10−5 для меди.

Магнитное поле индукции B представляет собой сумму вектора намагниченности M материала и напряженности внешнего магнитного поля H, где сумма умножается на константу проницаемости вакуума μ0, где

(4,183) B = μ0 ( H + M)

Индукционное магнитное поле B возникает из-за микроскопических (атомных) и макроскопических (проволочные) токов; тогда как напряженность магнитного поля H возникает только из-за макроскопических токов. Индукционное магнитное поле B будет стремиться выровнять дипольные моменты, потому что энергия меньше для параллельного выравнивания диполей.Индуцированное магнитное поле выровненных магнитных диполей M добавляет к приложенному извне магнитному полю H. Таким образом, магнитное поле составляет

(4,184) B = μ0 (1 + χm) H

Относительная проницаемость материала μr определяется как

(4,185) μr = 1 + χm

Материалы с относительной проницаемостью μr <1 являются диамагнитными. Материалы с μr> 1, но с μrÀ1 парамагнитны. Материалы с μrÀ1 являются ферромагнитными, а ферромагнитные материалы — нелинейными, поэтому χm и μr меняются в зависимости от напряженности приложенного магнитного поля H.

Магнитная проницаемость μ определяется как

(4,186) μ = μ0μr

В линейных магнитных материалах константа пропорциональности между индукционным магнитным полем B и напряженностью приложенного магнитного поля H является магнитной проницаемостью μ, где

( 4.187) B = мкГн

В нелинейных магнитных материалах, таких как кобальт, никель и мягкое железо, проницаемость μ изменяется в зависимости от приложенной напряженности магнитного поля H, где μ может быть большим и иметь репрезентативные значения в диапазоне от 250 для кобальта до 600 для никеля. и 5000 из мягкого железа.

Тепловое движение атомов, которое имеет тенденцию хаотизировать ориентацию диполей, должно преодолеваться приложенным магнитным полем или более низкими температурами. Восприимчивость при низких температурах и магнитных полях подчиняется закону Кюри, где для постоянной C характеристика материала равна

(4,188) χ = CT

Ферромагнетизм — это намагниченность, которая возникает в небольших областях материала без применения внешнего магнитного поля. поле. В ферромагнетиках естественная намагниченность, возникающая из-за неспаренных электронных спинов, достигает максимума при T = 0K и спадает до нуля при температуре Кюри TC.При температурах выше TC ферромагнитный материал становится парамагнитным, и его магнитная восприимчивость подчиняется модифицированному соотношению Кюри, в котором

(4.189) χ = CT − TC

Для температур ниже TC закон ферромагнетика Кюри больше не применим, потому что тогда материал становится ферромагнитным с постоянной намагниченностью. Ферромагнитный материал не намагничен в одном и том же направлении по всему объему, а скорее имеет множество меньших областей или доменов. Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагничивания меняется от одного домена к другому.Случайная ориентация доменов происходит потому, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле в некоторой степени выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля сверх магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. Когда внешнее магнитное поле удаляется, домены и их границы не возвращаются полностью к своей исходной ориентации, и, таким образом, домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий.

Напомним, что идентичные атомные электроны должны быть неразличимы (следовательно, полная волновая функция должна быть симметричной), но составляющие пространственные и спиновые волновые функции могут быть симметричными или асимметричными, если произведение волновых функций спина и пространственной составляющей равно асимметричный. В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние с минимальной энергией.Эта асимметрия полной волновой функции требует симметричного состояния спина, в котором спины неспаренных электронов ориентированы в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их параллельному выравниванию спинов в парамагнитных и ферромагнитных материалах.

Обменная сила или взаимодействие между пространственной и спиновой составляющими волновой функции для двух или более электронов отвечает за эту связь электронных спинов с параллельным выравниванием в парамагнитных и ферромагнитных материалах.В случае ферромагнетиков 3-D полоса заполнена не полностью, близкое расположение атомов железа делает неразличимыми электроны соседних атомов, а обменное взаимодействие теперь распространяется на электроны соседних атомов. Для поддержания полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (например, для атомов железа) пространственная волновая функция может быть асимметричной, а функция спина — симметричной.В этом случае кулоновская энергия сводится к минимуму за счет разделения электронов, но разделение позволяет неспаренным электронам иметь параллельные спины. Другая возможность состоит в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует, чтобы спины электронов были антипараллельны. Возможность антиферромагнетизма не минимизирует кулоновскую энергию в железе и не возникает.Однако такие материалы, как MnO ₂ , являются антиферромагнитными.

Глоссарий магнитных терминов

Ниже приводится глоссарий общих терминов, относящихся к магнитным материалам, дизайну и технике:

Воздушный зазор — это зазор с низкой магнитной проницаемостью на пути потока магнитной цепи. Часто воздух, но включает другие материалы, такие как краска, алюминий и т. Д.

Анизотропия, Буквально означает наличие различных свойств в зависимости от направления контроля.Магниты, которые являются анизотропными или имеют легкую ось намагничивания, имеют анизотропию, развиваемую двумя методами: формой и магнитокристаллическим.

As Площадь воздушного зазора, или площадь поперечного сечения воздушного зазора, перпендикулярного пути потока, представляет собой среднюю площадь поперечного сечения той части воздушного зазора, в которой происходит прикладное взаимодействие. Площадь измеряется в кв. См. в плоскости, перпендикулярной центральной силовой линии воздушного зазора.

Am Площадь магнита , это площадь поперечного сечения магнита, перпендикулярного центральной силовой линии, измеренная в кв.см. в любой точке по его длине. В конструкции магнита Am обычно считается площадью в нейтральной части магнита.

B Магнитная индукция, — это магнитное поле, создаваемое силой поля H в данной точке. Это векторная сумма в каждой точке вещества напряженности магнитного поля и результирующей собственной индукции. Магнитная индукция — это поток на единицу площади, перпендикулярный направлению магнитного пути.

Bd Остаточная индукция — это любая магнитная индукция, которая остается в магнитном материале после удаления приложенного насыщающего магнитного поля, Hs.(Bd — магнитная индукция в любой точке кривой размагничивания: измеряется в гауссах.)

Bd / Hd , Наклон рабочей линии, представляет собой отношение остаточной индукции Bd к размагничивающей силе Hd. Его также называют коэффициентом проницаемости, линией сдвига, линией нагрузки и единичной проницаемостью.

BdHd Energy product, указывает энергию, которую магнитный материал может подавать во внешнюю магнитную цепь при работе в любой точке своей кривой размагничивания; измеряется в мегагаусс-эрстедах.

(BH) max Максимальное произведение энергии, — это максимальное произведение (BdHd), которое может быть получено на кривой размагничивания.

Bis , (или Дж) Собственная индукция насыщения — это максимальная собственная индукция, возможная в материале.

Bg , Магнитная индукция в воздушном зазоре, — среднее значение магнитной индукции по площади воздушного зазора, А; или это магнитная индукция, измеренная в определенной точке внутри воздушного зазора; измеряется в гауссах.

Bi (или J) ​​Собственная индукция, — это вклад магнитного материала в общую магнитную индукцию B. Это векторная разность между магнитной индукцией в материале и магнитной индукцией, которая существовала бы в вакууме под одинаковой напряженности поля, H. Эта связь выражается уравнением:

Bi = B-H, где: Bi = собственная индукция в гауссах; B = магнитная индукция в Гауссах; H = напряженность поля в эрстедах.

Bm, Индукция отдачи, — это магнитная индукция, которая остается в магнитном материале после намагничивания и подготовки к окончательному использованию; измеряется в гауссах.

Bo, Магнитная индукция, в точке максимального энергетического продукта (BH) max; измеряется в гауссах.

Br, Остаточная индукция (или плотность потока), — магнитная индукция, соответствующая нулевой силе намагничивания в магнитном материале после насыщения в замкнутой цепи; измеряется в гауссах.

Состояние замкнутой цепи возникает, когда внешний путь потока постоянного магнита ограничен материалом с высокой проницаемостью.

Температура Кюри, Температура перехода, выше которой сплав теряет свои магнитные свойства. Это не максимально допустимая температура, которая обычно намного ниже.

Кривая размагничивания — это второй (или четвертый) квадрант основной петли гистерезиса. Точки на этой кривой обозначены координатами Bd и Hd.

Домены, Области в магнитном сплаве, имеющие одинаковую ориентацию. Магнитные домены — это области, где атомные моменты атомов взаимодействуют и допускают общий магнитный момент.Это домены, которые вращаются и управляются внешним намагничивающим полем, чтобы создать полезный магнит, который имеет чистый магнитный момент. В немагнитном материале домены не ориентированы и компенсируют друг друга. В этом состоянии нет чистого внешнего поля.

Вихревые токи, — это циркулирующие электрические токи, которые индуцируются в электропроводящих элементах при воздействии изменяющихся магнитных полей, создавая силу, противоположную магнитному потоку.Вихревые токи могут использоваться для выполнения полезной работы (например, гашения движения) или могут быть нежелательными последствиями определенных конструкций, которые следует учитывать или сводить к минимуму.

Электромагнит, представляет собой магнит, состоящий из соленоида с железным сердечником, в котором магнитное поле существует только во время протекания тока через катушку.

f Коэффициент сопротивления, учитывает кажущееся сопротивление магнитной цепи. Этот коэффициент необходим из-за того, что H и H рассматриваются как константы.

F Коэффициент утечки, учитывает утечку потока из магнитной цепи. Это соотношение между магнитным потоком в нейтральной части магнита и средним потоком, присутствующим в воздушном зазоре. F = (B мА м) / (B, A г).

F Магнитодвижущая сила, (разность магнитных потенциалов), представляет собой линейный интеграл напряженности поля H между любыми двумя точками, p1 и p2.
p2
F =? H dl
p1
F = магнитодвижущая сила в гильбертах
H = напряженность поля в эрстедах
dl = элемент длины между двумя точками в сантиметрах.

Ферромагнитный материал, — это материал, проницаемость которого намного больше 1 (от 60 до нескольких тысяч раз 1) и который демонстрирует явление гистерезиса.

Flux — это состояние, существующее в среде, на которую действует сила намагничивания. Эта величина характеризуется тем фактом, что электродвижущая сила индуцируется в проводнике, окружающем поток, в любое время, когда поток изменяется по величине. Единица измерения потока — Максвелл.

Измеритель потока — это прибор, который измеряет изменение потокосцепления с помощью поисковой катушки.

Окрашивающие поля представляют собой поток рассеяния, особенно связанный с краевыми эффектами в магнитной цепи.

гаусс — это единица магнитной индукции B в электромагнитной системе cgs. Один гаусс равен одному максвеллу на квадратный сантиметр.

A Гаусс-метр — это прибор, который измеряет мгновенное значение магнитной индукции B.Его принцип действия обычно основан на одном из следующих факторов: эффекте Холла, ядерном магнитном резонансе (ЯМР) или принципе вращающейся катушки.

gilbert — единица магнитодвижущей силы F в электромагнитной системе cgs.

H Напряженность магнитного поля, (сила намагничивания или размагничивания), является мерой векторной магнитной величины, которая определяет способность электрического тока или магнитного тела индуцировать магнитное поле в данной точке; измеряется в эрстедах.

Hc Коэрцитивная сила материала равна размагничивающей силе, необходимой для уменьшения остаточной индукции Br до нуля в магнитном поле после намагничивания до насыщения; измеряется в эрстедах.

Hci Собственная коэрцитивная сила материала, <, указывает на его сопротивление размагничиванию. Она равна размагничивающей силе, которая уменьшает внутреннюю индукцию Bi в материале до нуля после намагничивания до насыщения; измеряется в эрстедах.

Hd — это значение H, соответствующее остаточной индукции, Bd; на кривой размагничивания, измеряется в эрстедах.

Hmv — это значение H, соответствующее индукции отдачи, B; измеряется в эрстедах.

Ho, — напряженность магнитного поля в точке максимального произведения энергии (BH) max; измеряется в эрстедах.

Hs, Чистая эффективная сила намагничивания, это сила намагничивания, необходимая в материале для намагничивания до насыщения, измеренная в эрстедах.

Петля гистерезиса — это замкнутая кривая, полученная для материала путем нанесения (обычно в прямоугольных координатах) соответствующих значений магнитной индукции B для ординат и силы намагничивания H для абсцисс, когда материал проходит полный цикл между определенные пределы либо силы намагничивания, H, либо магнитной индукции. Б.

Необратимые потери определяются как частичное размагничивание магнита, вызванное воздействием высоких или низких температур внешних полей или других факторов.Эти потери можно возместить перемагничиванием. Магниты можно стабилизировать от необратимых потерь путем частичного размагничивания, вызванного температурными циклами или внешними магнитными полями.

Дж, см. Bi Собственная индукция.
Js, см. Bis, Собственная индукция насыщения.

Держатель представляет собой кусок (или кусочки) мягкого железа, который помещается на полюсные поверхности постоянного магнита или между ними, чтобы уменьшить сопротивление воздушного зазора и тем самым уменьшить утечку магнитного потока из магнита.Это также снижает восприимчивость магнита к размагничивающим воздействиям.

Хранители , Хранители — это материал с высокой проницаемостью, обычно низкоуглеродистая сталь, который устанавливается на магнит или магнитный узел для уменьшения сопротивления магнитной цепи. Это уменьшает общие поля утечки, создаваемые магнитом или магнитным узлом. Держатели обычно устанавливаются, чтобы помочь магниту или магнитному узлу противостоять размагничиванию во время обращения, транспортировки или хранения.Держатели обычно находятся на магнитах Alnico и магнитных узлах Alnico.

Изгиб кривой размагничивания — это точка, в которой кривая B-H перестает быть линейной. Все магнитные материалы, даже если их кривые во втором квадранте прямолинейны при комнатной температуре, при некоторой температуре развиваются изгибы. Alnico 5 показывает колено при комнатной температуре. Если рабочая точка магнита опускается ниже колена, небольшие изменения H вызывают большие изменения B, и магнит не сможет восстановить свой исходный выходной магнитный поток без повторного намагничивания.

Поток утечки — это поток ø, путь которого выходит за пределы полезной или предполагаемой магнитной цепи; измеряется в максвеллах.

lg Длина воздушного зазора , — длина пути центральной магнитной линии воздушного зазора; измеряется в сантиметрах.

lm Длина магнита, — это общая длина материала магнита, проходящего за один полный оборот центральной линии магнитной цепи; измеряется в сантиметрах.

лм / диаметр Отношение размеров , это отношение длины магнита к его диаметру или диаметра круга с эквивалентной площадью поперечного сечения.Для простых геометрических фигур, таких как стержни и стержни, отношение размеров связано с наклоном рабочей линии магнита BdHa.

Линия нагрузки — это линия, проведенная от начала кривой размагничивания с наклоном B / H, пересечение которой с кривой B-H представляет рабочую точку магнита. Также см. Коэффициент проницаемости.

Магнитные сборки, Комбинация материалов, магнитных и немагнитных, которые образуют конкретное решение.Включает постоянный магнит в качестве генератора потока и обычно использует низкоуглеродистую сталь для передачи потока к рабочей поверхности. Позволяет улучшить средства крепления резьбовых отверстий, резьб, прессовой посадки и т. Д.

Магнитная цепь , узел, состоящий из некоторых или всего следующего: постоянные магниты, ферромагнитные проводящие элементы, воздушные зазоры и электрические токи.

Магнитная длина, Физическая длина измерения магнита, которая соответствует направлению намагничивания магнита.Это может быть направление ориентации магнита, а может и не быть.

Основная петля гистерезиса материала — это замкнутая петля, полученная, когда материал циклически переключается между положительным и отрицательным насыщением.

maxwell — это единица измерения магнитного потока в электромагнитной системе cgs. Один максвелл — это одна линия магнитного потока.

Нейтральная секция постоянного магнита определяется плоскостью, проходящей через магнит перпендикулярно его центральной магнитной линии в точке максимального магнитного потока.

Северный полюс — это полюс магнита, который при свободном подвешивании будет указывать на северный магнитный полюс Земли. Определение полярности может сбивать с толку, и часто лучше всего уточнить, используя в спецификациях «северный полюс поиска» вместо «северный полюс».

oersted — единица измерения напряженности магнитного поля H в электромагнитной системе cgs. Один эрстед равен магнитодвижущей силе в один гильбер на сантиметр пути потока.

Состояние разомкнутой цепи возникает, когда намагниченный магнит сам по себе не имеет внешнего пути потока из материала с высокой проницаемостью.

Рабочая линия для данной цепи постоянного магнита — это прямая линия, проходящая через начало кривой размагничивания с наклоном отрицательного Bd / Hd. (Также известна как линия коэффициента проницаемости.)

Рабочая точка постоянного магнита — это точка на кривой размагничивания, определяемая координатами (BdHd), или точка на кривой размагничивания, определяемая координатами (BmHm).

Направление ориентации — это направление, в котором анизотропный магнит должен намагничиваться для достижения оптимальных магнитных свойств. Также известна как «ось», «легкая ось» или «угол наклона».

Ориентированный (анизотропный) материал — это материал, который имеет лучшие магнитные свойства в заданном направлении.

Парамагнитный материал, — материал, проницаемость которого немного превышает 1.

Пермеаметр — это прибор, который может измерять и часто записывать магнитные характеристики образца.

P Проницаемость, — величина, обратная сопротивлению R, измеренному в максвеллах на гильберт.

Полюса, — это ферромагнитные материалы, размещенные на магнитных полюсах, которые используются для придания формы и изменения эффекта линий магнитного потока.

R Сопротивление в некоторой степени аналогично электрическому сопротивлению. Это величина, которая определяет магнитный поток ø, возникающий в результате заданной магнитодвижущей силы F.
Где: R = F / ø
R = сопротивление, в гильбертах на максвелл
F = магнитодвижущая сила, I gilberts
Ø = поток в максвеллах.

Обратный путь — это проводящие элементы в магнитной цепи, которые обеспечивают путь с низким сопротивлением для магнитного потока.

Насыщение, Состояние, при котором увеличение приложенного внешнего поля не приводит к увеличению индукции. Когда это условие выполняется, все элементарные магнитные моменты имеют одинаковое выравнивание. Это условие важно для сплавов с постоянными магнитами и ферромагнитных сплавов. Магнитные сплавы всегда должны быть намагничены до насыщения.Магнит нельзя использовать на этом уровне, но перед кондиционированием и стабилизацией магнит всегда необходимо сначала намагнитить до насыщения. Обычно не следует превышать насыщение в ферромагнитных сплавах, которые составляют элементы ярма или обратного пути магнитной цепи. Если ферромагнитные элементы насыщены, в системе будет утечка магнитного потока, и следует рассмотреть возможность изменения конструкции.

Поисковая катушка представляет собой спиральный проводник, обычно с известной площадью и числом витков, который используется с измерителем потока для измерения изменения магнитной связи с катушкой.

Спеченный, Спеченный магнит состоит из спрессованного порошка, который затем подвергается операции термообработки, при которой достигается полная плотность и магнитная ориентация.

Стабилизация, — это воздействие на магнит размагничивающих воздействий, которые могут возникнуть при использовании, чтобы предотвратить необратимые потери во время реальной работы. Размагничивающие воздействия могут быть вызваны высокими или низкими температурами или внешними магнитными полями.

Tc, температура Кюри, это температура перехода, выше которой материал теряет свои магнитные свойства.

T max Максимальная рабочая температура, — максимальная температура, которой может подвергаться магнит без значительной нестабильности на больших расстояниях или структурных изменений.

Обратимые температурные коэффициенты — это изменения потока, которые происходят при изменении температуры. Они самопроизвольно восстанавливаются, когда температура возвращается к исходной точке.Магнитное насыщение материала существует, когда увеличение силы намагничивания не приводит к увеличению собственной индукции.

Температурный коэффициент — это коэффициент, который описывает обратимое изменение магнитных свойств при изменении температуры. Магнитное свойство самопроизвольно возвращается, когда температура возвращается к исходной точке. Обычно это выражается в процентах изменения на единицу температуры.

Неориентированный (изотропный) материал имеет одинаковые магнитные свойства во всех направлениях.

Vg Объем воздушного зазора, — полезный объем воздуха или немагнитного материала между магнитными полюсами; измеряется в кубических сантиметрах.

Weber , практическая единица магнитного потока. Это величина магнитного потока, который, будучи связан с однородной скоростью с однооборотным электрическим током в течение интервала в 1 секунду, будет индуцировать в этой цепи электродвижущий элемент силой 1 вольт.

µ магнитная проницаемость — это общий термин, используемый для выражения различных соотношений между магнитной индукцией B и напряженностью поля H.

µre проницаемость отдачи , это средний наклон петли гистерезиса отдачи. Также известен как второстепенная петля.

Магнитный поток ø, — это надуманная, но измеримая концепция, которая была разработана в попытке описать «поток» магнитного поля. Математически это поверхностный интеграл нормальной составляющей магнитной индукции B по площади A.
ø = ?? B • dA
, где:
ø = магнитный поток, в максвеллах
B = магнитная индукция, дюйм gauss
dA = элемент площади в квадратных сантиметрах
Когда магнитная индукция B равномерно распределена и перпендикулярна площади, A, поток ø = BA.

Молекулярные выражения: электричество и магнетизм

Эксперимент Фарадея по индукции магнитного поля Когда Майкл Фарадей сделал свое открытие электромагнитной индукции в 1831 году, он предположил, что изменяющееся магнитное поле необходимо для индукции тока в соседней цепи. Чтобы проверить свою гипотезу, он сделал катушку, обмотав бумажный цилиндр проволокой.Он подключил катушку к гальванометру, а затем перемещал магнит вперед и назад внутри цилиндра. Щелкните и перетащите магнит назад и вперед внутри катушки. Когда вы перемещаете магнит вперед и назад, обратите внимание, что стрелка гальванометра движется, указывая на то, что в катушке индуцируется ток. Также обратите внимание, что стрелка немедленно возвращается в ноль, когда магнит не движется. Фарадей подтвердил, что для возникновения электромагнитной индукции необходимо движущееся магнитное поле. НАЗАД К РУКОВОДСТВАМ ПО ЭЛЕКТРИЧЕСТВЕ И МАГНЕТИЗМУ Вопросы или комментарии? Отправить нам письмо. © 1995-2021, автор — Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения правообладателей. Использование этого веб-сайта означает, что вы соглашаетесь со всеми юридическими положениями и условиями, изложенными владельцами. Этот веб-сайт поддерживается нашим Команда разработчиков графики и веб-программирования в сотрудничестве с оптической микроскопией в Национальной лаборатории сильного магнитного поля . Последнее изменение: пятница, 31 марта 2017 г., 10:10 Счетчик доступа с 6 сентября 1999 г .: 2174679

Правило правой руки | PASCO

Правило правой руки в физике

Правило правой руки — это мнемоника руки, используемая в физике для определения направления осей или параметров, указывающих в трех измерениях.Правило правой руки, изобретенное в XIX веке британским физиком Джоном Амброузом Флемингом для применения в электромагнетизме часто используется для определения направления третьего параметра, когда известны два других (магнитное поле, ток, магнитная сила). Есть несколько вариантов правила правой руки, которые объясняются в этом разделе.

Когда проводник, такой как медный провод, движется через магнитное поле (B), в проводнике индуцируется электрический ток (I).Это явление известно как закон индукции Фарадея. Если проводник перемещается внутри магнитного поля, то существует соотношение между направлениями движения (скорости) проводника, магнитного поля и индуцированного тока. Мы можем использовать правило правой руки Флеминга исследовать закон индукции Фарадея, который представлен уравнением:

ЭДС = индуцированная ЭДС (V или J / C)
N = количество витков катушки
Δ𝚽 _B = изменение магнитного потока (Тм2)
Δ t = изменение во времени (с)

Поскольку оси x, y и z перпендикулярны друг другу и образуют прямые углы, правило правой руки можно использовать для визуализации их выравнивание в трехмерном пространстве.Чтобы использовать правило правой руки, начните с создания L-образной формы с помощью большого пальца правой руки, указателя и середины. Палец. Затем переместите средний палец внутрь к ладони так, чтобы он был перпендикулярен указательным и большим пальцам. Твоя рука должно выглядеть примерно так:

На диаграмме выше большой палец совмещен с осью z, указательный палец — с осью x, а средний палец — с осью y.

Беспроводная интеллектуальная тележка

Один из лучших способов помочь учащимся обрести уверенность в использовании правила правой руки — это провести наглядную демонстрацию, которая поможет им распознать и исправить свои неправильные представления об ортогональных отношениях и системах координат.

Многие учителя используют вращающуюся линейку, чтобы показать, что объект, который кажется вращающимся «по часовой стрелке» с точки зрения одного ученика, также кажется вращающимся «против часовой стрелки», если смотреть с другой точки зрения. Использование динамической тележки для обучения правилу правой руки позволяет преподавателям продемонстрировать как проблему с помощью терминологии «по часовой стрелке», так и «против часовой стрелки», а также решение, которое обеспечивают правило правой руки и оси вращения. С беспроводной интеллектуальной тележкой преподаватели могут использовать 3-осевой гироскоп и фиксированную систему координат для создания увлекательных демонстраций вращательного движения.Ознакомьтесь с полной демонстрацией здесь.

Правило правой руки для магнетизма

---

Движущиеся заряды

Заряженная частица — это частица с электрическим зарядом. Когда неподвижная заряженная частица существует в магнитном поле, она не испытать магнитную силу; однако, как только заряженная частица движется в магнитном поле, она испытывает наведенное магнитное поле. сила, которая смещает частицу с ее первоначального пути. Это явление, также известное как сила Лоренца, согласуется с правилом, что утверждает, что «магнитные поля не работают.”Уравнение, используемое для определения величины магнитной силы, действующей на заряженную частицу (q) перемещение магнитного поля (B) со скоростью v под углом θ составляет:

Если скорость заряженной частицы параллельна магнитному полю (или антипараллельна), то силы нет, потому что sin (θ) равен нулю. Когда это происходит, заряженная частица может сохранять прямолинейное движение даже в присутствии сильного магнитного поля.

Плоскость, образованная направлением магнитного поля и скоростью заряженной частицы, расположена под прямым углом к ​​силе.Поскольку сила возникает под прямым углом к ​​плоскости, образованной скоростью частицы и магнитным полем, мы можем использовать правило правой руки, чтобы определить их ориентацию.

Правило правой руки гласит: чтобы определить направление магнитной силы на положительный движущийся заряд, направьте большой палец правой руки в направление скорости (v), указательный палец в направлении магнитного поля (B) и средний палец будут указывать в направление результирующей магнитной силы (F).На отрицательные заряды будет действовать сила в противоположном направлении.

Магнитная сила, индуцированная током: ток в прямом проводе

Обычный ток состоит из движущихся зарядов, которые имеют положительный характер. Когда обычный ток проходит по проводящему проводу, на провод действует магнитное поле, которое его толкает. Мы можем использовать правило правой руки, чтобы определить направление силы, действующей на токоведущий провод. В этой модели ваши пальцы указывают в направлении магнитного поля, а большой палец — в направлении магнитного поля. обычный ток, протекающий через провод, и ваша ладонь указывает направление, в котором провод проталкивается (сила).

Магнитная сила, действующая на провод с током, определяется уравнением:

Когда длина провода и магнитное поле расположены под прямым углом друг к другу, уравнение принимает следующий вид:

F _B = магнитная сила (Н)
I = ток (A)
L = длина провода (м)
B = магнитное поле (Тл)

Если рассматривать протекание тока как движение носителей положительного заряда (обычный ток) в приведенном выше image, мы замечаем, что обычный ток движется вверх по странице.Поскольку обычный ток состоит из положительных зарядов, то тот же провод с током также может быть описан как имеющий ток с отрицательным носители заряда движутся вниз по странице. Хотя эти токи движутся в противоположных направлениях, один наблюдается магнитная сила, действующая на провод. Следовательно, сила действует в том же направлении, независимо от того, рассмотрите поток положительных или отрицательных носителей заряда на изображении выше. Применение правила правой руки к направление обычного тока указывает направление магнитной силы, которое должно быть направлено вправо.Когда мы рассматриваем поток отрицательных носителей заряда на изображении выше, правило правой руки указывает на то, что направление силы, которую нужно оставить; однако отрицательный знак меняет результат на противоположный, указывая на то, что направление магнитной силы действительно указывает вправо.

Если мы рассмотрим поток зарядов в двух разных проводах, один с положительными зарядами, текущими вверх по странице, а другой с отрицательными зарядами, текущими вверх по странице, то направление магнитных сил не будет таким же, потому что мы рассматриваем две разные физические ситуации.В первом проводе поток положительных зарядов вверх по странице указывает на то, что по странице стекают отрицательные заряды. Правило правой руки говорит нам, что магнитный сила укажет в правильном направлении. По второму проводу вверх по странице текут отрицательные заряды, которые означает, что положительные заряды стекают по странице. В результате правило правой руки показывает, что магнитная сила указывает в левом направлении.

Токи, индуцированные магнитными полями

В то время как магнитное поле может быть индуцировано током, ток также может быть индуцирован магнитным полем.Мы можем использовать второе правило правой руки, иногда называемое правилом захвата правой руки, для определения направления магнитного поле, созданное током. Чтобы использовать правило захвата правой рукой, направьте большой палец правой руки в направлении течения. течь и скручивай пальцы. Направление ваших пальцев будет отражать направление искривления индуцированного магнитного поля.

Правило захвата правой рукой особенно полезно для решения проблем, связанных с токоведущим проводом или соленоидом. В обеих ситуациях правило захвата правой рукой применяется к двум приложениям закона оборота Ампера, который связывает интегрированное магнитное поле вокруг замкнутого контура к электрическому току, проходящему через плоскость замкнутого контура.

Направление вращения: соленоиды

Когда электрический ток проходит через соленоид, он создает магнитное поле. Чтобы использовать правило захвата правой рукой в проблема с соленоидом, укажите пальцами в направлении обычного тока и оберните пальцы, как будто они были вокруг соленоида. Ваш большой палец будет указывать в направлении силовых линий магнитного поля внутри соленоида. Примечание что силовые линии магнитного поля вне соленоида направлены в противоположном направлении. Они охватывают изнутри, чтобы снаружи соленоида.

Направление вращения: токоведущие провода

Когда электрический ток проходит по прямому проводу, он индуцирует магнитное поле. Чтобы применить правило захвата правой рукой, совместите большой палец с направлением обычного тока (от положительного к отрицательному), и ваши пальцы будут указывать направление магнитных линий потока.

Правило правой руки для крутящего момента

---

Проблемы с крутящим моментом часто являются самой сложной темой для студентов-первокурсников-физиков.К счастью, есть правило правой руки приложение для крутящего момента. Чтобы использовать правило правой руки в задачах с крутящим моментом, возьмите правую руку и наведите ее на направление вектора положения (r или d), затем поверните пальцы в направлении силы, и большой палец укажет в направлении крутящего момента.

Уравнение для расчета величины вектора крутящего момента для крутящего момента, создаваемого заданной силой:

Когда угол между вектором силы и плечом момента является прямым, синусоидальный член становится 1 и уравнение становится:

F = сила (Н)
𝜏 = крутящий момент (Нм)
r = расстояние от центра до линии действия (м)

Положительный и отрицательный крутящие моменты

Моменты, возникающие против часовой стрелки, являются положительными.В качестве альтернативы крутящие моменты, возникающие в по часовой стрелке — отрицательные моменты. Так что же произойдет, если ваша рука укажет на бумагу или из нее? Крутящие моменты, которые лицевой стороной наружу из бумаги следует анализировать как положительный крутящий момент, а крутящий момент, направленный внутрь, следует анализировать. как отрицательные моменты.

Правило правой руки для перекрестного произведения

---

Перекрестное произведение или векторное произведение создается, когда упорядоченная операция выполняется над двумя векторами, a и b. В векторное произведение векторов a и b перпендикулярно как a, так и b и перпендикулярно плоскости, которая его содержит.С есть два возможных направления для перекрестного произведения, для определения направления следует использовать правило правой руки вектора кросс-произведения.

Например, векторное произведение векторов a и b можно представить с помощью уравнения:

(произносится как «крест б»)

Чтобы применить правило правой руки к перекрестным произведениям, выровняйте пальцы и большой палец под прямым углом. Затем укажите свой индекс пальцем в направлении вектора a и средним пальцем в направлении вектора b.Ваш большой палец правой руки укажет в направлении векторного произведения a x b (вектор c).

Правило правой руки для закона Ленца

---

Закон электромагнитной индукции Ленца — еще одна тема, которая часто кажется нелогичной, поскольку требует понимание того, как магнетизм и электрические поля взаимодействуют в различных ситуациях. Закон Ленца гласит, что направление тока, индуцируемого в замкнутом проводящем контуре изменяющимся магнитным полем (закон Фарадея), такова, что вторичное магнитное поле, созданное индуцированным током, противодействует начальному изменению магнитного поля, которое произвело Это.Так что это значит? Давайте разберемся с этим.

Когда магнитный поток через проводник с замкнутым контуром изменяется, он индуцирует ток внутри контура. Индуцированная ток создает вторичное магнитное поле, которое противодействует первоначальному изменению потока, которое инициировало индуцированный ток. Сила магнитного поля, проходящего через катушку из проволоки, определяет магнитный поток. Магнитный поток зависит от сила поля, площадь катушки и относительная ориентация между полем и катушкой, как показано в следующем уравнении.

𝚽 _B = магнитный поток (Tm ² )
B = магнитное поле (Тл)
Θ = угол между полем и нормалью (град.)
A = площадь контура (м ² )

Чтобы понять, как закон Ленца повлияет на эту систему, нам нужно сначала определить, является ли начальное магнитное поле увеличение или уменьшение силы. Когда северный магнитный полюс приближается к петле, это вызывает существующее магнитное поле. поле для увеличения.Поскольку магнитное поле увеличивается, индуцированный ток и результирующее индуцированное магнитное поле будут противодействовать исходному магнитному полю, уменьшая его. Это означает, что первичное и вторичное магнитные поля будут возникать в противоположные направления. Когда существующее магнитное поле уменьшается, индуцированный ток и результирующее индуцированное магнитное поле поле будет противодействовать исходному, уменьшая магнитное поле, усиливая его. Таким образом, индуцированное магнитное поле будет иметь в том же направлении, что и исходное магнитное поле.

Чтобы применить правило правой руки к закону Ленца, сначала определите, увеличивается ли магнитное поле, проходящее через петлю, или уменьшается. Напомним, что магниты создают силовые линии магнитного поля, которые движутся от северного магнитного полюса в направлении магнитный южный полюс. Если магнитное поле увеличивается, то направление вектора индуцированного магнитного поля будет в обратном направлении. Если магнитное поле в контуре уменьшается, то вектор индуцированного магнитного поля будет происходят в том же направлении, чтобы заменить уменьшение исходного поля.Затем выровняйте большой палец в направлении индуцированное магнитное поле и скрученные пальцы. Ваши пальцы будут указывать в направлении индуцированного тока.

В какой момент магнитная индукция станет нулевой?

В контексте этого вопроса, который, как я понимаю, означает, что оба проводника несут постоянный (и предположительно равный) ток, я могу только предположить (см. Примечание ниже), что вы запрашиваете набор точек, где суммарное магнитное поле генерируемый током в проводниках равен нулю.

В качестве примечания, магнитная индукция относится к созданию электродвижущей силы (напряжения) в проводнике из-за изменения магнитного поля. Поскольку ваш вопрос не относится к источнику магнитного поля, кроме самих проводников, я предполагаю, что вместо этого вы спрашиваете о магнитном поле, генерируемом током. Если это не так, я буду рад изменить свой ответ

Теперь давайте подумаем о том, где магнитные поля от двух перпендикулярных проводов будут равны нулю.Магнитные поля должны точно нейтрализовать друг друга, что означает, что величина каждого из них должна быть одинаковой, а направление должно быть прямо противоположным. Последнее ограничение на направление подразумевает, что векторы магнитного поля должны быть в одной плоскости и иметь противоположные направления.

Имея в виду эти ограничения, мы можем попытаться визуализировать часть магнитных полей, изобразив 2 полые трубы, перпендикулярные друг другу, встречающиеся на стыке (это было бы намного проще, если бы можно было разместить изображения, но я постараюсь описать Это).Если бы вы соединили две трубы путем сварки, как бы выглядели линии сварки? Это будет выглядеть как 2 пересекающихся кольца, образующих форму X (если смотреть сверху), вроде рамки шара.

Эти 2 кольца представляют собой набор точек в трехмерном пространстве, где величины магнитного поля от каждого провода равны для заданного расстояния (радиуса) от каждого провода. Если вы учли все возможные расстояния от 0 до бесконечности, вы можете визуализировать это как наборы концентрических колец, расширяющихся наружу.

Итак, теперь, когда мы определили места, где величины равны, давайте посмотрим на направление. Давайте возьмем всего 1 набор из 2 перпендикулярных колец и посмотрим на направления векторов магнитного поля от каждого провода на каждом кольце. Для простоты для каждого кольца нам нужно смотреть только на 4 точки на кольце — 12 часов, 3 часа, 6 часов и 9 часов. В каких направлениях показаны силовые линии в каждой точке? Если вы установите направление тока в каждом проводе (неважно, в каком направлении, если вы сохраняете его постоянным) и примените правило правой руки, вы обнаружите, что на обоих кольцах, на 12 и 6 часах. позиции — это когда векторы находятся точно под прямым углом, а позиции на 3 и 9 часов — это когда векторы либо находятся в одном направлении на 1 кольце, либо в противоположных направлениях на другом кольце.

Итак, только на 1 кольце есть набор точек (точнее, 2), где величины силовых линий равны И направления векторов противоположны. Теперь помните, что каждый набор из 2 колец представляет собой фиксированное расстояние от провода, на котором величины силовых линий равны. Таким образом, вам нужно учитывать все возможные расстояния, которые представляют собой просто концентрические наборы из двух пересекающихся колец. Таким образом, экстраполируя ваш случай с фиксированным расстоянием, вы видите, что набор всех точек, где линии поля сокращаются, представляет собой диагональную линию.

Следовательно, ответ состоит в том, что набор точек, в которых магнитные поля от двух перпендикулярных проводов, по которым проходят одинаковые токи, суммируются до нуля, представляет собой диагональную линию под углом 45 градусов в плоскости проводов, которая проходит через точку их пересечения. Через какие квадранты проходит линия, зависит от направления тока в двух проводах.

2 примечания на другой стороне:

— Угол диагональной линии зависит от величин токов в проводах.Если токи равны, то угол составляет 45 градусов. Если они не равны, то угол изменится на

— Основываясь на симметрии, другая симметричная диагональная линия, проходящая через другие 2 квадранта, будет набором точек, в которых магнитное поле является максимальным (точно аддитивным).

Закон Био-Савара и магнитная индукция

Закон Био-Савара

Био и Савар провели множество экспериментов, чтобы определить факторы, от которых зависит магнитное поле, обусловленное током в проводнике.

Результаты экспериментов обобщены в виде закона Био-Савара.

Рассмотрим проводник XY, по которому течет ток I (рис. 3.10). AB = d l — небольшой элемент проводника. P — точка на расстоянии r от средней точки O отрезка AB. Согласно Био и Савару, магнитная индукция в дБ при P из-за элемента длиной d l составляет

1. прямо пропорциональна току (I)

2.прямо пропорциональна длине элемента (d l )

3. прямо пропорциональна синусу угла между d l и линией, соединяющей элемент d l и точкой P (sin θ)

Направление дБ перпендикулярно плоскости, содержащей текущий элемент Id l и r (т.е. плоскость бумаги), и действует внутрь. Единица магнитной индукции — тесла (или) Вебер м-2.

1. Магнитная индукция из-за бесконечно длинного прямого проводника, по которому проходит ток

XY — это бесконечно длинный прямой проводник, по которому проходит ток I (рис. 3.11). P — точка на расстоянии a от проводника. АВ представляет собой небольшой элемент длиной d l . θ — угол между текущим элементом I d l и линией, соединяющей элемент d l и точку P.Согласно закону Био-Савара, магнитная индукция в точке P, обусловленная элементом тока Id l , составляет

2. Магнитная индукция вдоль оси круговой катушки, по которой проходит ток

Давайте рассмотрим круговую катушку радиуса ‘ a ‘ с током I, как показано на рис. 3.12. P — точка вдоль оси катушки на расстоянии x от центра O катушки.

Направление дБ перпендикулярно текущему элементу Id l и CP. Следовательно, он расположен по PR перпендикулярно CP.

Учитывая диаметрально противоположный элемент A’B ‘, величина дБ в точке P из-за этого элемента такая же, как для AB, но его направление вдоль PM. Пусть угол между осью катушки и линией, соединяющей элемент (d l ) и точкой (P), равен α.

дБ делится на две составляющие: — дБ sin α вдоль OP и дБ cos α перпендикулярно OP.Компоненты дБ cos α из-за двух противоположных элементов компенсируют друг друга, тогда как компоненты дБ sin α складываются. Таким образом, общая магнитная индукция в точке P, создаваемая всей катушкой, составляет

3. Гальванометр касательной

Гальванометр касательной — это устройство, используемое для измерения тока. Он работает по принципу касательного закона. Магнитная стрелка, подвешенная в точке, где есть два пересекающихся поля под прямым углом друг к другу, остановится в направлении равнодействующей двух полей.

Конструкция

Он состоит из круглой катушки с проволокой, намотанной на немагнитный каркас из латуни или дерева. Вертикальная рама установлена ​​на горизонтальном круглом поворотном столе с тремя регулировочными винтами. Вертикальная рама может вращаться вокруг своего вертикального диаметра.

В центре поворотного стола есть небольшой вертикальный выступ, на котором установлен компас.

Коробка компаса состоит из небольшого вращающегося магнита, к которому под прямым углом прикреплена тонкая длинная алюминиевая стрелка. Алюминиевый указатель может перемещаться по круговой шкале с градуировкой в ​​градусах. Шкала состоит из четырех квадрантов. Коробка компаса поддерживается таким образом, чтобы центр вращающейся магнитной стрелки совпадал с центром катушки. Поскольку магнитное поле в центре катушки однородно на очень небольшой площади, используется небольшая магнитная игла, чтобы она оставалась в однородном поле даже в отклоненном положении.