Калькулятор импеданса последовательной RC-цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет импеданс и фазовый сдвиг для последовательно соединенных конденсатора и резистора для заданной частоты синусоидального сигнала.
Пример. Рассчитать импеданс конденсатора 500 мкФ и резистора 0,2 Ом на частоте 25 кГц.
Входные данные
Сопротивление, R
миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)
Емкость, С
фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)
Частота, f
герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц)
Выходные данные
Угловая частота ω= рад/с
Емкостное реактивное сопротивление XC= Ом
Полный импеданс RC |ZRC|= Ом
Фазовый сдвигφ = ° = рад
Введите значения сопротивления, емкости и частоты, выберите единицы измерения и нажмите кнопку Рассчитать.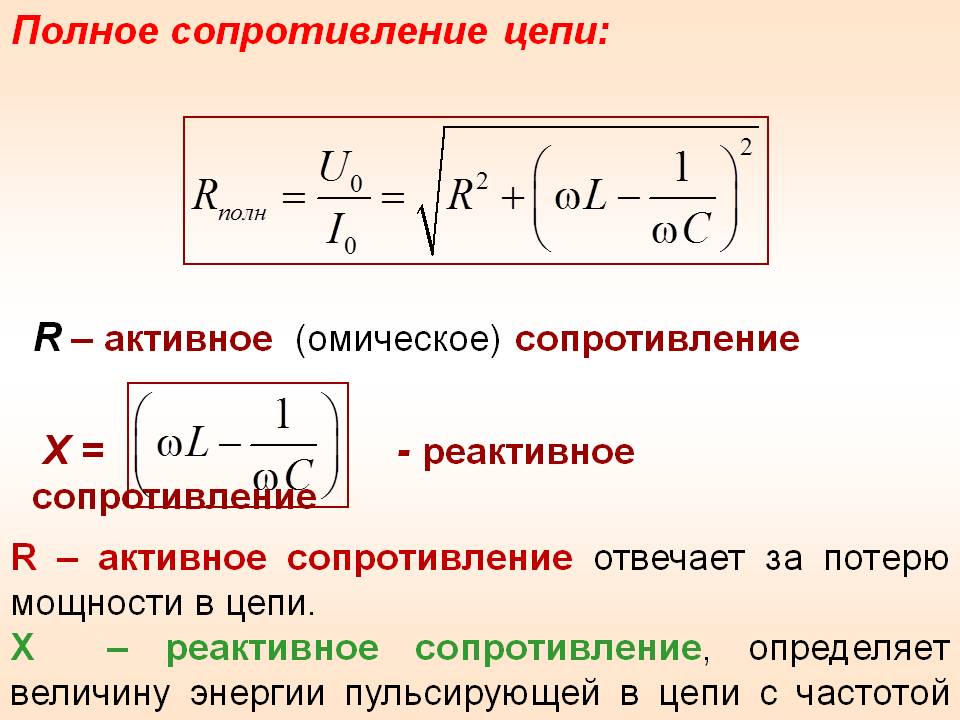 Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.
Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.
Для расчетов используются указанные ниже формулы:
Здесь
ZLC — импеданс цепи LC в омах (Ом),
ω = 2πf — угловая частота в рад/с,
f — частота в герцах (Гц),
R сопротивление в омах (Ом),
C — емкость в фарадах (Ф),
φ — фазовый сдвиг между полным напряжением VT и полным током IT в градусах (°) или радианах и
j — мнимая единица
Для расчета введите емкость, сопротивление, частоту и выберите единицы измерения. Импеданс RC -цепи будет показан в омах, сдвиг фаз в градусах и радианах. Также будет рассчитано емкостное реактивное сопротивление.
График зависимости импеданса ZRC последовательной RC-цепи от частоты f при различных величинах сопротивления и емкости показывает обратно пропорциональную зависимость импеданса от частоты
Векторная диаграмма последовательной RC-цепи показывает, что общий ток отстает от общего напряжения на угол от 0 до 90°. Отметим, что если закоротить резистор, то угол будет равен 90° (чисто реактивная нагрузка), а если закоротить конденсатор, то угол будет равен 0° (чисто активная нагрузка)
Отметим, что если закоротить резистор, то угол будет равен 90° (чисто реактивная нагрузка), а если закоротить конденсатор, то угол будет равен 0° (чисто активная нагрузка)
Простейшая RC-цепь состоит из резистора и конденсатора, соединенных последовательно и питающихся от общего источника напряжения. Через конденсатор и резистор течет один и тот же ток, потому что они соединены последовательно. Напряжения на конденсаторе VC и резисторе VR показаны на диаграмме под прямым углом друг к другу. Их сумма всегда больше, чем полное напряжение VT.
Если посмотреть на приведенную выше формулу для расчета импеданса, можно заметить, что она выглядит как уравнение для расчета гипотенузы прямоугольного треугольника. Это связано с тем, что в графической форме импеданс последовательной RC-цепи выглядит так, как показано выше на векторной диаграмме, где активное сопротивление R находится на горизонтальной оси, а реактивное сопротивление XC находится на вертикальной оси. Гипотенуза полученного прямоугольного треугольника является импедансом цепи , а фазовый угол — это угол между горизонтальной осью и вектором импеданса.
Гипотенуза полученного прямоугольного треугольника является импедансом цепи , а фазовый угол — это угол между горизонтальной осью и вектором импеданса.
Фазовый угол изменяется от 0° для чисто резистивной цепи до –90° для чисто емкостной цепи. Из треугольника напряжений получаем:
Фазовый угол определяется с помощью обратной функции (арктангенса):
В последовательной RC-цепи с источником синусоидального сигнала синусоида тока опережает синусоиду напряжения на угол от 0° (для чисто резистивной цепи) до 90° (для чисто емкостной цепи). Иными словами, напряжение отстает от тока по фазе на угол φ (0° ≤ φ ≤ 90°.). Если напряжение V выразить в форме V = Vmsin(2πft), то ток I будет равен I = Imsin(2πft – φ), где Vm и Im — амплитуды напряжения и тока, f — частота (постоянная величина), φ — фазовый угол (также постоянная величина) и t — время (переменная величина)
В последовательной RL-цепи один и тот же ток протекает через катушку и резистор. Напряжение на катушке VC отстает от общего тока на 90°, а на резисторе находится в фазе с током. Согласно второму закону Кирхгофа (для напряжений), сумма падений напряжения на элементах цепи должна быть равна общему напряжению VT. Напряжения на резисторе VR и конденсаторе VC сдвинуты по фазе на 90°, поэтому они складываются с помощью векторной диаграммы и полное напряжение определяется по формуле:
Напряжение на катушке VC отстает от общего тока на 90°, а на резисторе находится в фазе с током. Согласно второму закону Кирхгофа (для напряжений), сумма падений напряжения на элементах цепи должна быть равна общему напряжению VT. Напряжения на резисторе VR и конденсаторе VC сдвинуты по фазе на 90°, поэтому они складываются с помощью векторной диаграммы и полное напряжение определяется по формуле:
Отметим, что полное напряжение всегда меньше суммы падений напряжения на резисторе и катушке — точно так же, как в прямоугольном треугольнике гипотенуза всегда меньше суммы катетов.
Режимы отказа элементов
А что если в этой схеме отказал один из элементов? Нажмите на соответствующую ссылку, чтобы посмотреть соответствующие режимы отказа:
Особые режимы работы цепи
Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:
Различные режимы работы на постоянном токе
Короткое замыкание
Обрыв цепи
Чисто емкостная цепь
Примечания
- Нулевая частота в объяснениях поведения этой цепи означает постоянный ток.
 Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения. - При нулевой частоте реактивное сопротивление конденсатора считается нулевым, если его емкость бесконечно большая. Если же емкость конденсатора конечная или нулевая, его реактивное сопротивление бесконечно большое и для источника постоянного напряжения он представляет собой обрыв цепи, иными словами отсутствующий конденсатор.
Импеданс — Физическая энциклопедия
ИМПЕДАНС (англ, impedance, от лат. impedio — препятствую) (комплексное сопротивление) — аналог электрич. сопротивления для гармонич. процессов. Различают И. элемента цепи перем. тока (И. двухполюсника) н И. к—л. поверхности в монохроматич. эл—магн. поле (полевой И., поверхностный И.).
Понятие И. было введено в электродинамику О. Хевисайдом (О. Heaviside) и О. Лоджем (О. Lodge), понятие полевого И.- С. Щелкуновым (S. Schelkunoff, 1938). Импедансные характеристики используют не только в электродинамике, их вводят для описания линий передачи волновых возмущений любой природы (см. , напр., Импеданс акустический).
, напр., Импеданс акустический).
Импеданс двухполюсника. В теории электрич. цепей любую часть цепи, состоящую из пассивных линейных элементов (таких, как сопротивления r, индуктивности L, ёмкости С
Z (w) = V/I =R (w) + iX(w).
Рис. 1. Электрическая цепь, включающая пассивные линейные элементы и имеющая два полюса: a — схема цепи; б — эквивалентный двухполюсник с импедансом Z(w).
Здесь V — комплексная амплитуда напряжения между полюсами 1 и 2, I — комплексная амплитуда тока в направлении от полюса 1 к полюсу 2; R — веществ. часть импеданса (активное сопротивление),  (реактивное сопротивление, реактанс). Модуль И. |Z|=(R2+X2)1/2 наз. полным сопротивлением двухполюсника. В СИ И. измеряется в Омах, в Гаусса системе единиц имеет размерность, обратную скорости. Иногда наряду с И. Z используют обратную ему величину s=Z-1, наз. адмитансом.
Активное сопротивление R ответственно за потери энергии, поступающей в двухполюсник. Мощность потерь Р (средняя за период колебаний Т=2p/w)выражается соотношением
Р =R|I|2/2.
Реактанс характеризует величину энергии, пульсирующей с частотой 2w (и потому в среднем за период равной нулю), накапливаемой в двухполюснике и отдаваемой обратно источнику. Знак реактанса определяется зависимостью от времени: в технике и прикладной физике (и в данной статье) полагают её в теоретич.
физике обычно принимают В случае чисто индуктивного двухполюсника (
(реактивное сопротивление, реактанс). Модуль И. |Z|=(R2+X2)1/2 наз. полным сопротивлением двухполюсника. В СИ И. измеряется в Омах, в Гаусса системе единиц имеет размерность, обратную скорости. Иногда наряду с И. Z используют обратную ему величину s=Z-1, наз. адмитансом.
Активное сопротивление R ответственно за потери энергии, поступающей в двухполюсник. Мощность потерь Р (средняя за период колебаний Т=2p/w)выражается соотношением
Р =R|I|2/2.
Реактанс характеризует величину энергии, пульсирующей с частотой 2w (и потому в среднем за период равной нулю), накапливаемой в двухполюснике и отдаваемой обратно источнику. Знак реактанса определяется зависимостью от времени: в технике и прикладной физике (и в данной статье) полагают её в теоретич.
физике обычно принимают В случае чисто индуктивного двухполюсника (
Z
Матрица импеданса. Разветвлённую электрич. цепь, имеющую более двух точек подключения, наз. многополюсником [если число пар точек подключения (входов) равно N, то цепь наз. 2N-полюсником]. На входах многополюсника должны быть заданы направления отсчёта напряжений и токов (рис. 2). Если многополюсник включает в себя только линейные, пассивные и
взаимные элементы, то для квазистационарных гармонич. процессов все его внеш. свойства описываются матрицей импеданса ||Zab||, связывающей комплексные амплитуды напряжений и токов на входах при произвольном подключении к когерентным источникам:
2). Если многополюсник включает в себя только линейные, пассивные и
взаимные элементы, то для квазистационарных гармонич. процессов все его внеш. свойства описываются матрицей импеданса ||Zab||, связывающей комплексные амплитуды напряжений и токов на входах при произвольном подключении к когерентным источникам:
Напр., для четырёхполюсника, изображённого на рис. 3, а, элементы матрицы И. равны: Z11=Z1+Z3, Z22=Z2+Z3, Z12=Z21=Z3. В силу взаимности принципа матрица ||Zab|| симметрична, т. е. Zab=Zba
Входной импеданс. Свойства многополюсников можно описать и с помощью т. н. входных И. отд. входов.
Рис. 2. Многополюсник, все внешние свойства которого задаются матрицей импеданса ||Z||.
Рис. 3. Четырёхполюсник: a — эквивалентная схема; б — схема для определения входного импеданса.
При этом по отношению к выбранному входу многополюсник рассматривают как двухполюсник, а все остальные входы считают нагруженными произвольными И. Zнb. Поэтому входные И. являются ф-циями не только частоты, но и нагрузочных И. Так, для четырёхполюсника, приведённого на рис. 3:
Для согласования произвольной нагрузки Zн с источником, имеющим внутр. И. Zвн, используют недиссипативные четырёхполюсники (без поглощающих элементов), добиваясь выполнения условия Zвх(Zн)=Z*вн (* означает комплексное сопряжение). При этом достигается макс. передача энергии от источника к нагрузке (кпд равен 50%, остальная энергия поглощается внутри источника). Если требуется обеспечить высокий кпд передачи, выбирают такой согласующий четырёхполюсник, чтобы выполнялись условия: R
Волновой импеданс. Входной И. четырёхполюсника, удовлетворяющий условию Zвх(Zн=Zв)=Zн= Zв, наз. волновым импедансом, ибо в бесконечной цепочке, составленной из одинаковых четырёхполюсников, будут без отражений распространяться волны (в общем случае экспоненциально затухающие) с пост. значением отношения напряжения к току. В пределе непрерывной однородной линии передачи это отношение в любой нормальном сечении постоянно и при отсутствии потерь равно Z
Входной И. четырёхполюсника, удовлетворяющий условию Zвх(Zн=Zв)=Zн= Zв, наз. волновым импедансом, ибо в бесконечной цепочке, составленной из одинаковых четырёхполюсников, будут без отражений распространяться волны (в общем случае экспоненциально затухающие) с пост. значением отношения напряжения к току. В пределе непрерывной однородной линии передачи это отношение в любой нормальном сечении постоянно и при отсутствии потерь равно Z
Г=(Zн-Zв)/(Zн+Zв). (1)
При Z Длинные линии не являются квазистационарными системами, поэтому понятие напряжения является условным. Обычно его относят только к точкам, лежащим в одном нормальном сечении линии Sn, а путь
интегрирования g12 выбирают лежащим в этом же сечении
Длинные линии не являются квазистационарными системами, поэтому понятие напряжения является условным. Обычно его относят только к точкам, лежащим в одном нормальном сечении линии Sn, а путь
интегрирования g12 выбирают лежащим в этом же сечении
Поверхностный (полевой) импеданс вводят для
монохроматич. эл—магн. полей Е(r)exp(iwt), H(r)exp(iwt) на любой условной поверхности S след. образом:
где Et, Нt
 безразмерен, а в СИ имеет размерность сопротивления. Иногда для И. в системе единиц Гаусса используют выражение при этом имеет размерность сопротивления.
Эл—магн. волны разных типов (моды) характеризуются разл. полевыми И., задаваемыми на волновых фронтах. Так, для поперечной плоской волны (типа ТЕМ), распространяющейся в направлении
безразмерен, а в СИ имеет размерность сопротивления. Иногда для И. в системе единиц Гаусса используют выражение при этом имеет размерность сопротивления.
Эл—магн. волны разных типов (моды) характеризуются разл. полевыми И., задаваемыми на волновых фронтах. Так, для поперечной плоской волны (типа ТЕМ), распространяющейся в направлении где k — волновое число, k|| — продольная компонента волнового вектора. Для критич. частот (
т.
 е. в первом случае речь идёт о преимуществ. запасе электрич. энергии (ёмкостный И.), во втором — магнитной (индуктивный И.).
При отсутствии потерь полевой И. для распространяющихся волн — величина действительная; иногда её наз. волновым сопротивлением среды, поскольку она обладает мн. свойствами волнового сопротивления линии или цепочки четырёхполюсников. В частности, при падении плоской волны из среды 1 на плоскую границу раздела со средой 2 коэф. отражения (по амплитудам полей) аналогично (1) выражается в виде
е. в первом случае речь идёт о преимуществ. запасе электрич. энергии (ёмкостный И.), во втором — магнитной (индуктивный И.).
При отсутствии потерь полевой И. для распространяющихся волн — величина действительная; иногда её наз. волновым сопротивлением среды, поскольку она обладает мн. свойствами волнового сопротивления линии или цепочки четырёхполюсников. В частности, при падении плоской волны из среды 1 на плоскую границу раздела со средой 2 коэф. отражения (по амплитудам полей) аналогично (1) выражается в виде Это выражение представляет собой Френеля формулы ,записанные через И. (р-поляризации соответствует мода ТМ, s-поляризации — мода ТЕ, (k||/k)(1,2)=cosq(l,2), q(l) и q(2) — углы падения и преломления). При исследовании отражения от плоскослоистых неоднородных сред часто ур-ния для полей преобразуют в ур-ния для полевых И., при этом порядок ур-ний понижается.
 Существенны т. н. импедансные поверхности, т. е. поверхности с заданным, фиксированным на них значением полевого И. Фактически фиксация осуществляется (в большинстве случаев приближённо), когда структура поля «под поверхностью» неизменна и определяется к—л. свойствами среды или формирующих поле устройств. Так, при падении волны на хорошо поглощающую среду волна уходит в глубь среды почти по нормали, независимо от угла падения, следовательно, «входной» И. можно считать фиксированным и
равным Z(2)TEM (Леонтовича граничное условие). С помощью импедансных поверхностей моделируют границы направляющих устройств в антеннах, замедляющих системах и т. д. Лит.: Основы теории цепей, 4 изд., М., 1975; Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред, 2 изд., М., 1982; Будурис Ж., Шеневье П., Цепи сверхвысоких частот, пер. с франц., М., 1979.
Г. В. Пермитин, М. А. Миллер.
Существенны т. н. импедансные поверхности, т. е. поверхности с заданным, фиксированным на них значением полевого И. Фактически фиксация осуществляется (в большинстве случаев приближённо), когда структура поля «под поверхностью» неизменна и определяется к—л. свойствами среды или формирующих поле устройств. Так, при падении волны на хорошо поглощающую среду волна уходит в глубь среды почти по нормали, независимо от угла падения, следовательно, «входной» И. можно считать фиксированным и
равным Z(2)TEM (Леонтовича граничное условие). С помощью импедансных поверхностей моделируют границы направляющих устройств в антеннах, замедляющих системах и т. д. Лит.: Основы теории цепей, 4 изд., М., 1975; Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред, 2 изд., М., 1982; Будурис Ж., Шеневье П., Цепи сверхвысоких частот, пер. с франц., М., 1979.
Г. В. Пермитин, М. А. Миллер.Предметный указатель >>
переменный ток
Индуктивное сопротивление определяется по формуле:
При прохождении переменного тока в цепи с реактивным сопротивлением происходит выделение теплоты???
Активным называется сопротивление, которое обусловлено переходом энергии электрического тока во внутреннюю энергию
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных резистора, конденсатора и катушки индуктивности:
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных резистора и конденсатора:
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных резистора и катушки индуктивности:
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных конденсатора и катушки индуктивности (активное сопротивление катушки индуктивности равно 0):
Емкостное
сопротивление . . . от частоты переменного
тока. обратно
пропорционально зависит
. . от частоты переменного
тока. обратно
пропорционально зависит
Активное сопротивление . . . от частоты переменного тока Не зависит
Если угол сдвига фаз между током и напряжением в цепи переменного тока имеет положительное значение, то цепь обязательно содержит катушку индуктивности
Укажите формулу для определения импеданса цепи переменного тока, состоящей из последовательно соединенных катушки индуктивности и резистора:
При уменьшении частоты переменного тока индуктивное сопротивление Уменьшится
При уменьшении частоты переменного тока емкостное сопротивление Увеличится
При уменьшении частоты переменного тока активное сопротивление Не изменится
Укажите формулу для определения импеданса цепи переменного тока, состоящей из последовательно соединенных катушки индуктивности и резистора:
??
Укажите формулу для определения импеданса цепи переменного тока, состоящей из последовательно соединенных конденсатора и катушки индуктивности:
Укажите формулу для определения импеданса цепи переменного тока, состоящей из последовательно соединенных резистора, катушки индуктивности и конденсатора:
Активное
сопротивление цепи проявляется в . .
.выделении теплоты в
цепи
.
.выделении теплоты в
цепи
Импедансом называется полное сопротивление цепи
Сдвиг фаз между током и напряжением в цепи переменного тока, содержащей катушку индуктивности, резистор и конденсатор определяется по формуле:
ВЕРНО
Емкостное сопротивление уменьшается с увеличение частоты переменного тока.
Импеданс-полное сопротивление цепи переменного тока.
На векторной диаграмме напряжений цепи переменного тока вектор амплитуды напряжения на конденсаторе направлен перпендикулярно оси тока.
Активное сопротивление цепи не зависит от частоты переменного тока
Единицей СИ индуктивного сопротивления является ОМ
Переменный ток-ток, изменяющийся во времени
На векторной диаграмме напряжение в цепи тока вектор амплитуды напряжения на резисторе совпадают по направлению с осью тока
Реактивное сопротивление цепи переменного тока обусловлено наличием в ней конденсаторов и катушек индуктивности
При прохождении переменного тока на активном сопротивлении происходит выделение теплоты
Переменный ток в цепи с конденсатором опережает напряжение в фазе на П\2
При увеличении частоты переменного тока индуктивное сопротивление увеличивается
Угол сдвига фаз между током в цепи переменного тока, содержащий конденсатор, имеет отрицательное значение
НЕВЕРНО
Реактивно сопротивление включает емкостное и активное сопротивление
Переменный то-ток, изменяющийся только по гармоническому закону
В цепи переменного тока всегда происходит сдвиг фаз между силой тока и напряжением
Величина(модуль) реактивного сопротивления равен сумме сопротивлений конденсатора и резистора
При увеличении частоты переменного тока емкостное сопротивление увеличивается
В цепи переменного тока сила и напряжение всегда совпадают
Величина(модуль) реактивного сопротивления равен сумме индуктивного сопротивлений цепи переменного тока
Единицей СИ емкостного сопротивления является генри ( Гн)
Единицей СИ индуктивного сопротивления является фарад (Ф)
Активное
сопротивление цепи зависит от частоты
переменного тока.
При прохождении переменного тока в реактивном сопряжении происходит выделение теплоты
Ток в цепи переменного тока, содержащей катушку индуктивности, по фазе совпадает с напряжением
Последовательная RLC-цепь
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
Напряжение на зажимах цепи
или
где
Выполнив подстановку, получим
Подставим в последнее выражение ток в цепи, зная, что он равен
В итоге получим выражение
Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.
Сдвиг фаз RLС-цепи можно определить по формуле
Полное сопротивление RLС-цепи
Амплитудное значение тока
При построении векторной диаграммы RLC-цепи возможны три случая:
1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.
При этом в такой цепи наблюдается резонанс напряжений.
2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.
На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.
Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.
Пример задачи
Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Найдем напряжение на каждом из элементов
И общее в цепи
Сдвиг фаз равен
Векторная диаграмма
Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.
Глава 17. Резонансные цепи . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Написать формулы для определения емкостного и индуктивного сопротивления.
• Описать, как реагируют на переменный ток и напряжение конденсаторы и катушки индуктивности.
• Дать определение реактивного сопротивления последовательной цепи и уметь определить характер цепи (индуктивный или емкостный).
• Дать определение термина импеданс.
• Уметь вычислять импеданс, который содержит как резистивную, так и емкостную или индуктивную составляющие.
• Объяснить, как должен быть модифицирован закон Ома перед использованием его для цепей переменного тока.
• Уметь вычислять Хс, XL, X, Z и Iт в последовательных RLC цепях.
• Уметь вычислять Ic, IL, Ix, IR и Iz в параллельных RLC цепях.
В предыдущих главах сопротивление, емкость и индуктивность в цепях переменного тока рассматривались по отдельности. В этой главе исследуется комбинация сопротивления, емкости и индуктивности в цепи переменного тока. Рассматриваемые вопросы не являются новым материалом, но применяют все изложенные ранее принципы.
Когда реактивное сопротивление катушки индуктивности равно реактивному сопротивлению конденсатора в цепи, возникает резонанс. Резонансные цепи широко используются в электронике.
Резонансные цепи широко используются в электронике.
17-1. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
Емкостное реактивное сопротивление — это противодействие, которое конденсатор оказывает переменному току. Оно измеряется в омах и обозначается символом Хс. Емкостное реактивное сопротивление вычисляется по формуле:
Хс = 1/2πfC
Заметим, что при использовании этой формулы емкость должна быть выражена в фарадах (а не в долях фарады).
Индуктивное реактивное сопротивление — это противодействие, которое катушка индуктивности оказывает переменному току. Оно измеряется в омах и обозначается символом XL. Индуктивное реактивное сопротивление вычисляется по формуле:
XL = 2πfL.
Заметим, что при использовании этой формулы индуктивность должна быть выражена в генри (а не в долях генри).
Емкостное реактивное сопротивление служит причиной того, что ток опережает по фазе напряжение. Индуктивное реактивное сопротивление служит причиной того, что ток отстает по фазе от напряжения. Емкостное и индуктивное реактивные сопротивления прямо противоположны по создаваемым эффектам и, следовательно, когда в цепи присутствуют и индуктивность и емкость, общий эффект определяется разностью их значений. Эта разность называется реактивным сопротивлением и обозначается символом X. Реактивное сопротивление может быть выражено следующими формулами:
X = Хс — XL или X = XL — Хс.
ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 10 генри (рис. 17-1), работающей на частоте 60 герц?
Рис. 17-1
17-1
Дано:
f = 60 Гц; L = 10 Гн; С = 1 мкФ
Х =?
Решение:
Хс = 1/2πfC
Хс =1/(6,28)(60)(0,000001)
Хс =2654 Ом
XL = 2πfL
XL = (6,28)(60)(10)
XL = 3768 Ом
X = XL- XC = 3768–2654
X = 1114 Ом (индуктивное).
ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 1 генри (рис. 17-2), работающей на частоте 60 герц?
17-2), работающей на частоте 60 герц?
Рис. 17-2
Дано:
f = 60 Гц; L = 1 Гн; С = 1 мкФ
Х =?
Решение:
Хс = 1/2πfC
Хс = 1/(6,28)(60)(0,000001)
Хс =2654 Ом
XL = 2πfL
XL = (6,28)(60)(1)
XL = 376,8 Ом
X = XC — XL = 2654 — 376,8
X = 2277,2 Ом (емкостное).
Эти примеры иллюстрируют важный момент. Когда емкостное и индуктивное реактивные сопротивления соединены последовательно, меньшее значение всегда вычитается из большего. Получающееся в результате реактивное сопротивление характеризуется большим значением.
Получающееся в результате реактивное сопротивление характеризуется большим значением.
17-1. Вопросы
1. Каково фазовое соотношение между током и напряжением на конденсаторе?
2. Каково фазовое соотношение между током и напряжением на катушке индуктивности?
3. По какой формуле определяется полное реактивное сопротивление последовательной цепи, когда известны значения Хс и XL?
4. Какова величина полного реактивного сопротивления (X) последовательной цепи, содержащей Хс = 50 ом и XL = 20 ом? Укажите, является X емкостным или индуктивным.
17-2. ИМПЕДАНС
Реактивное сопротивление, как емкостное, так и индуктивное, противодействует протеканию тока в цепях переменного тока. Активное сопротивление также препятствует протеканию тока в цепи.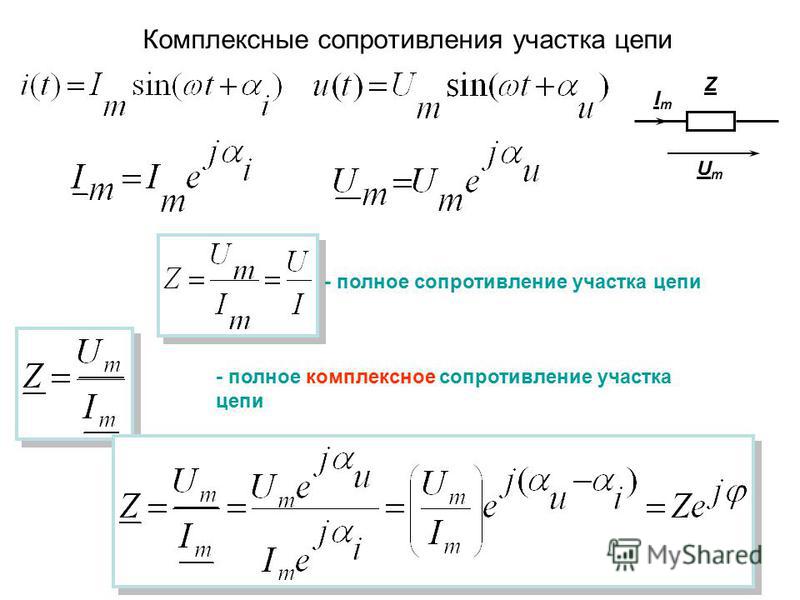 Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.
Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.
И активное, и реактивное сопротивления измеряются в омах. Следовательно, кажется логичным сложить эти сопротивления для того, чтобы получить импеданс. Однако этого делать нельзя, поскольку активное и реактивное сопротивления — величины векторные. В цепях переменного тока, содержащих только активное сопротивление, ток и напряжение находятся в фазе. И ток, и напряжение достигают своих максимальных значений одновременно.
Как упоминалось ранее, в цепях переменного тока, содержащих только реактивные сопротивления, ток будет либо опережать, либо отставать от напряжения на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи.
Когда цепь содержит и активное, и реактивное сопротивление, импеданс будет больше любого их них.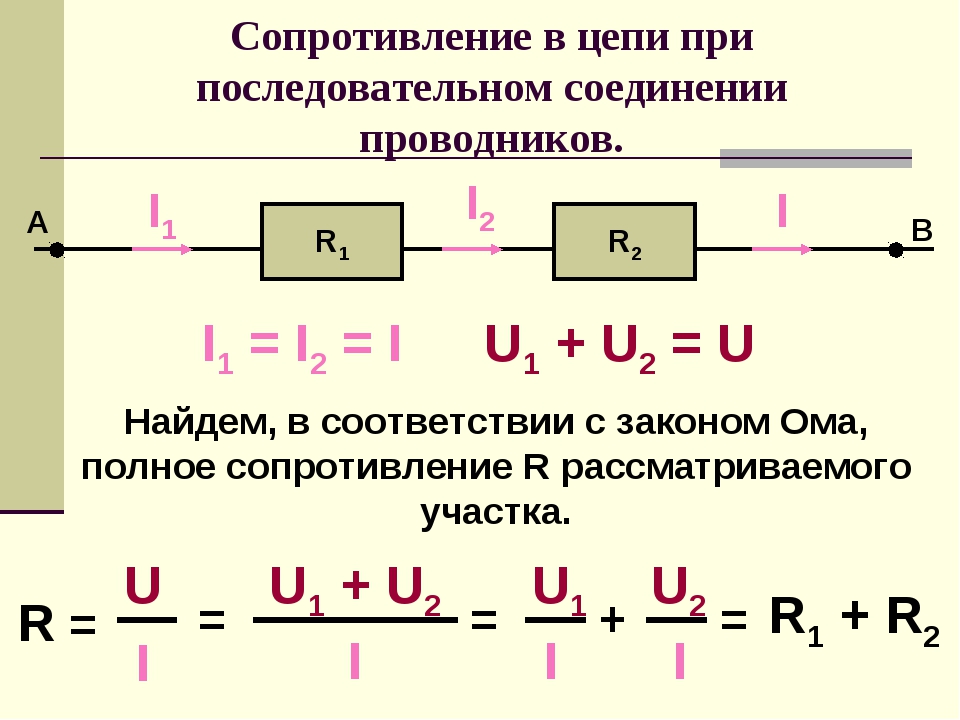 Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.
Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.
Для того чтобы найти импеданс, используется векторная диаграмма — прямоугольный треугольник сопротивлений. Это может быть сделано потому, что ток через резистор находится в фазе с напряжением на нем, а ток через реактивную нагрузку сдвинут по фазе на 90 градусов относительно напряжения на ней. Они находятся под прямым углом друг к другу.
ПРИМЕР: Чему равен импеданс последовательно соединенных резистора сопротивлением 150 ом и индуктивного реактивного сопротивления 100 ом?
В качестве первого шага нарисуем основание треугольника, представляющее резистор 150 ом. Далее нарисуем линию под углом 90 градусов к основанию, представляющую индуктивное сопротивление 100 ом. После этого соединим концы линий, образуя гипотенузу треугольника. Гипотенуза представляет импеданс цепи (рис. 17-3).
Рис.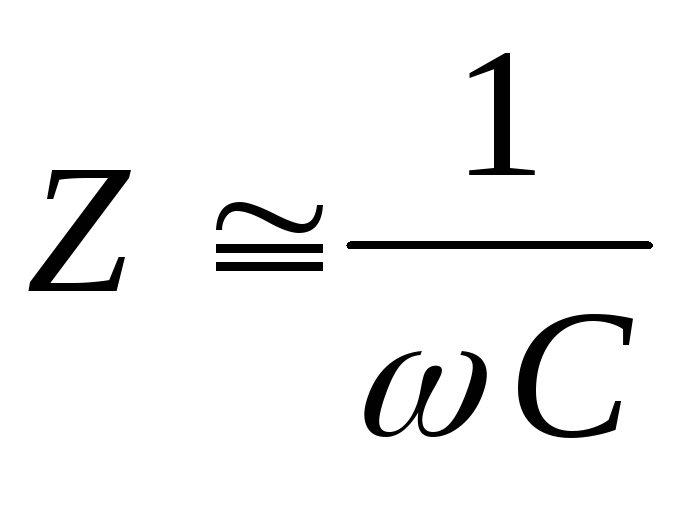 17-3. Векторная диаграмма.
17-3. Векторная диаграмма.
Теорема Пифагора утверждает:
с2 = а2 + Ь2,
где с — гипотенуза, а и b — катеты.
Графически это представлено на рис. 17-4.
Рис. 17-4. Векторная диаграмма, показывающая связь активного сопротивления, реактивного индуктивного сопротивления и импеданса в последовательной цепи.
Если импеданс, активное и реактивное сопротивления заменить соответствующими символами, то формула будет выглядеть следующим образом:
Z2 = R2 + X2.
Вернемся к определению импеданса последовательной комбинации резистора 150 ом и индуктивного сопротивления 100 ом.
Дано:
R = 150 Ом; XL = 100 Ом.
Решение:
Z2 = R2 + X2
Z2 =(150)2 + (100)2 = 32500
Z = √(32500) = 180,28 Ом.
Если вместо индуктивного в цепи находится емкостное сопротивление, то линию, представляющую емкостное сопротивление, обычно рисуют направленной вниз. Это показывает, что оно действует в направлении противоположном индуктивному сопротивлению, которое рисуют направленным вверх.
В последовательной цепи с емкостным реактивным сопротивлением формула для вычисления импеданса будет выглядеть следующим образом:
Z2 = R2 + Х2С.
ПРИМЕР: Чему равен импеданс цепи, содержащей резистор сопротивлением 220 ом, соединенный последовательно с конденсатором, имеющим емкостное реактивное сопротивление 270 ом?
Дано:
R = 220 Ом; Xc = 270 Ом.
Решение:
Z2 = R2 + X2c
Z2 = (220)2 + (270)2 = 121300
Z = √(121300) = 348,28 Oм.
Z = 348,28 Ом.
Если последовательная цепь содержит индуктивное и емкостное реактивные сопротивления, а также активное сопротивление, необходимо найти полное реактивное сопротивление (X). Реактивное сопротивление может быть либо индуктивным, либо емкостным. Следовательно, может быть использована одна из следующих формул:
Z2 = R2 + X2L;
Z2 = R2 + Х2с.
17-2. Вопросы
1. Как называется полное противодействие в цепи переменного тока?
2. Какая формула используется для вычисления величины полного противодействия в последовательной цепи?
3. Чему равно значение Z в последовательной цепи переменного тока, где Хс = 3 Ом, XL = 6 Ом, a R = 4 Ом?
17-3 ЗАКОН ОМА
Закон Ома не может быть применен в цепях переменного тока потому, что он не учитывает реактивное сопротивление. Модифицируя закон Ома путем учета импеданса, можно получить общий закон, который применим к цепям переменного тока.
I = E/R преобразуется в I = E/Z
Эта формула применима к переменному току, текущему в любой цепи.
ПРИМЕР: Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 250 ом и емкостное сопротивление 150 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?
Дано:
R = 510 Ом; XL = 250 Ом; Xc = 150 Ом; E = 120 В
Решение:
X = ХL + Хc = 250–150
X = 100 Ом (индуктивное)
Z2 = R2 + X2
Z2 =(510)2 +(100)2
Z = √(270100)
Z = 519,71 Ом
I = E/Z = 120/519,71
I = 0,23 А или 230 мА.
17-3. Вопросы
1. Каким образом модифицируется закон Ома, чтобы его можно было применить к цепям переменного тока для определения напряжения и тока?
2. Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 300 ом и емкостное сопротивление 375 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?
17-4. ЦЕПИ RLC
Материал, изложенный до сих пор, применим ко всем цепям переменного тока. В приведенных примерах рассматривались последовательные цепи. Понятия, рассмотренные в этом параграфе, не содержат нового материала, но используют все принципы, изложенные ранее.
ПРИМЕР: На рис. 17-5 показана последовательная RLC цепь. Необходимо вычислить Хс, XL, X, Z и IT.
Рис. 17-5. Последовательная цепь RLC.
Сначала вычислим Хс, XL и X.
Дано:
f = 60 Гц; С = 470 мкФ; L = 27 мГн.
Решение:
Xc = 1/2πfC
Xc = 1/(6,28)(60)(0,000470)
XC = 5,65 Ом
XL = 2πfL
XL = (6,28)(60)(0,027)
XL = 10,17 Ом
X = XL — Xc = 10,17 — 5,65
X = 4,52 Ом (индуктивное).
Используем значение X для вычисления Z.
Дано:
X = 4,52 Ом; R = 10 Ом.
Решение:
Z2 = R2 + X2
Z2 = (10)2 + (4,52)2 = 120,43
Z = √(120,43) = 10,97 Ом.
Это значение Z может быть использовано для вычисления полного тока (IT).
Дано:
Z = 10,97 Ом; E = 120 В.
Решение:
IT = E/Z = 120/10,97
IT = 10,94 A.
Помните, что во всех частях последовательной цепи течет один и тот же ток.
Если элементы в цепях соединены параллельно, то следует учесть одно главное различие между последовательными и параллельными цепями.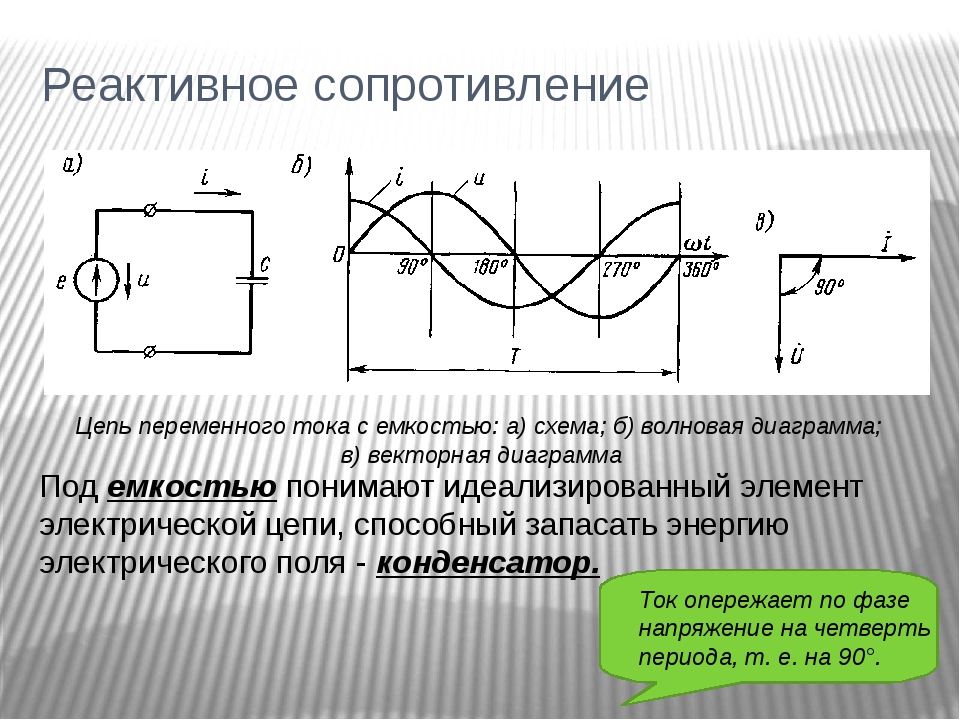 При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.
При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.
В последовательной цепи RLC для вычисления реактивного сопротивления и импеданса используются следующие формулы:
X = Хс — XL или X = XL — Хс, Z2 = R2 + X2.
В случае параллельных цепей должны использоваться следующие формулы:
IX = Iс — IL или IX = IL — IX; I2Z = (IR)2 + (IX)2
Импеданс параллельной цепи находится с помощью формулы:
IZ = E/Z
Замечание: Если неизвестно напряжение (Е), приложенное к цепи, то для вычисления Ic, IL, Ix, IR и IZ можно использовать любое значение Е. То же значение напряжения должно использоваться для вычисления импеданса.
То же значение напряжения должно использоваться для вычисления импеданса.
ПРИМЕР: Найти значение Z для цепи, показанной на рис. 17-6.
Рис. 17-6. Параллельная цепь RLC.
Дано:
Е = 120 В; R = 60 Ом; Хс = 75 Ом; XL = 50 Ом.
Решение:
Первым шагом в вычислении Z является вычисление токов отдельных ветвей.
IR = E/R = 120/60 = 2 A
Ix = E/Xc = 120/75 = 1,6 A
IL = E/XL = 120/50 = 2,4 A
Используя значения IR, Ic, IL, вычислим Ix и Iz
IX = IL — Ic = 2,4 – 1,6
Ix = 0,8 А (индуктивный)
I2z = (IR)2 + (Ix)2
I2z = (2)2 + (0,8)2 = 4,64
Iz = √(4,64) = 2,15 A.
Используя значение Iz, вычислим Z.
Iz = E/Z
2,15 = 120/Z
Z = 120/2,15 = 55,8 Ом
В завершение этой главы отметим, что мы рассмотрели все блоки, из которых строятся электрические цепи. При изложении материала использовались ранее изученные понятия и соотношения.
17-4. Вопрос
1. Чем отличаются вычисления импеданса для последовательной цепи переменного тока и для параллельной цепи?
РЕЗЮМЕ
• Конденсатор в цепи переменного тока оказывает противодействие любому изменению напряжения, так же как он это делает в цепи постоянного тока.
• Ток опережает по фазе напряжение на конденсаторе на 90 градусов.
• Противодействие, оказываемое конденсатором переменному току, называется емкостным реактивным сопротивлением. Оно обозначается Хс и вычисляется по формуле:
XC = 1/2πfC
• Катушка индуктивности в цепи переменного тока противодействует любому изменению тока, так же как она это делает в цепи постоянного тока.
• На катушке индуктивности ток отстает по фазе от напряжения на 90 градусов.
• Противодействие, оказываемое катушкой индуктивности переменному току, называется индуктивным реактивным сопротивлением. Оно обозначается XL и вычисляется по формуле
XL = 2πfL.
• Полное реактивное сопротивление последовательной цепи переменного тока определяется формулами X = XC — XL или X = XL — XC.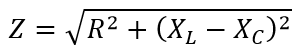
• Полное реактивное сопротивление последовательной цепи переменного тока является либо емкостным, либо индуктивным, в зависимости от того, какая величина больше, ХC или XL.
• В параллельной цепи реактивное сопротивление определяется с помощью формул
IZ = E/Z
где Iz определяется формулой Iz2 = (IR)2 + (IX)2, а Iх вычисляется по формуле IX = IC — IL или IX = IL — IC.
• Реактивное сопротивление параллельной цепи также может быть емкостным или индуктивным, в зависимости то того, какая величина больше IC или IL.
• Полное сопротивление цепи переменного тока называется импедансом. Он обозначается символом Z. В последовательной цепи Z2 = R2 + X2. В параллельной цепи I2Z = (IR)2 + (IX)2 и
IZ = E/Z
• Получена формула для закона Ома, который можно применять для пеней переменного тока:
I = E/Z
Глава 17. САМОПРОВЕРКА
1. Чему равны значения ХС, XL, X, Z и IT для цепи, изображенной на рис. 17-7?
Рис. 17-7. Последовательная цепь RLC.
2. Чему равны значения IC, IL, IX, IR и IZ для цепи, изображенной на рис. 17-8?
Чему равны значения IC, IL, IX, IR и IZ для цепи, изображенной на рис. 17-8?
Рис. 17-8. Параллельная цепь RLC.
Электрический импеданс — Electrical impedance
Противостояние цепи току при приложении напряжения
В электротехнике , электрическое сопротивление является мерой оппозиции , что через цепь представляет в виде тока , когда напряжение прикладывается.
Количественно импеданс двухконтактного элемента схемы представляет собой отношение комплексного представления синусоидального напряжения между его выводами к комплексному представлению тока, протекающего через него. В общем, это зависит от частоты синусоидального напряжения.
Импеданс расширяет концепцию сопротивления на переменном токе (AC) цепей, и обладает как величина и фаза , в отличие от сопротивления, который имеет только величину. Когда цепь приводится в действие постоянным током (DC), нет различия между импедансом и сопротивлением; последний можно рассматривать как импеданс с нулевым фазовым углом .
Импеданс — это комплексное число с теми же единицами измерения, что и сопротивление, для которого единицей СИ является ом ( Ом ). Его символ обычно Z , и он может быть представлен записью его величины и фазы в полярной форме | Z | ∠θ . Однако декартово представление комплексных чисел часто более эффективно для анализа схем.
Понятие импеданса полезно для выполнения анализа переменного тока электрических сетей , поскольку оно позволяет связывать синусоидальные напряжения и токи простым линейным законом. В нескольких портовых сетях, два терминала определение импеданса является недостаточным, но сложные напряжения на порты и тока , протекающие через них по — прежнему линейно связаны с помощью матрицы импеданса .
Обратный импеданс является проводимостью , которой СИ единицей является сименс , прежнего названия мксит .
Инструменты, используемые для измерения электрического импеданса, называются анализаторами импеданса .
Введение
Термин импеданс был введен Оливером Хевисайдом в июле 1886 года. Артур Кеннелли был первым, кто представил импеданс комплексными числами в 1893 году.
В дополнение к сопротивлению, наблюдаемому в цепях постоянного тока, импеданс в цепях переменного тока включает в себя эффекты индукции напряжений в проводниках магнитными полями ( индуктивность ) и электростатическое накопление заряда, вызванное напряжениями между проводниками ( емкость ). Импеданс, вызванный этими двумя эффектами, вместе называется реактивным сопротивлением и формирует мнимую часть комплексного импеданса, тогда как сопротивление формирует действительную часть.
Импеданс определяется как отношение напряжения к току в частотной области .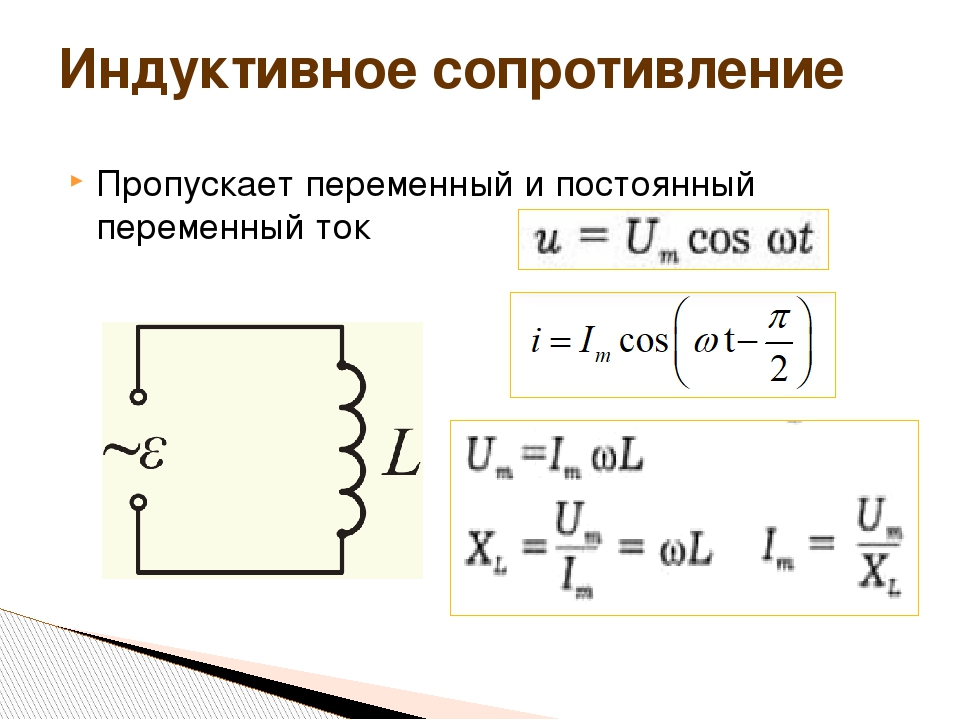 {j \ arg (Z)}}
{j \ arg (Z)}}
где величина представляет собой отношение амплитуды разности напряжений к амплитуде тока, а аргумент (обычно обозначаемый символом ) дает разность фаз между напряжением и током. является мнимой единицей и используется вместо этого в данном контексте, чтобы избежать путаницы с символом электрического тока . | Z | {\ displaystyle | Z |} аргумент ( Z ) {\ Displaystyle \ arg (Z)} θ {\ displaystyle \ theta} j {\ displaystyle j} я {\ displaystyle i}
В декартовой форме импеданс определяется как
- Z знак равно р + j Икс {\ Displaystyle \ Z = R + jX}
где действительная часть импеданса — это сопротивление, а мнимая часть — реактивное сопротивление . р {\ displaystyle R} Икс {\ displaystyle X}
Там, где необходимо добавить или вычесть импедансы, более удобна декартова форма; но когда количества умножаются или делятся, расчет становится проще, если используется полярная форма. Расчет схемы, такой как определение полного импеданса двух параллельных импедансов, может потребовать преобразования между формами несколько раз во время расчета. {j \ arg (Z)}}
{j \ arg (Z)}}
Величина импеданса действует так же, как сопротивление, давая падение амплитуды напряжения на импедансе для заданного тока . Фазовый коэффициент говорит нам, что ток отстает от напряжения на фазу (т. Е. Во временной области сигнал тока смещается позже по отношению к сигналу напряжения). | Z | {\ displaystyle | Z |} Z {\ displaystyle Z} я {\ displaystyle I} θ знак равно аргумент ( Z ) {\ Displaystyle \ тета \; = \; \ arg (Z)} θ 2 π Т {\ displaystyle {\ frac {\ theta} {2 \ pi}} T}
Подобно тому , как сопротивление распространяется закон Ома для цепи переменного тока, крышки других результатов анализа цепи постоянного тока, например, деления напряжения , ток деления , теоремы тевенина и теорема Нортона , также может быть распространено на цепь переменного тока путем замены сопротивления с сопротивлением.
Фазоры
Вектор представляет собой постоянное комплексное число, обычно выражаемое в экспоненциальной форме, представляющее комплексную амплитуду (величину и фазу) синусоидальной функции времени. {j \ omega t}}
{j \ omega t}}
Примеры устройств
Резистор
Фазовые углы в уравнениях для импеданса конденсаторов и катушек индуктивности указывают на то, что напряжение на конденсаторе отстает от тока через него на фазу , в то время как напряжение на катушке индуктивности опережает ток через него . Одинаковые амплитуды напряжения и тока указывают на то, что величина импеданса равна единице. π / 2 {\ displaystyle \ pi / 2} π / 2 {\ displaystyle \ pi / 2}Импеданс идеального резистора является чисто реальным и называется резистивным сопротивлением :
- Z р знак равно р {\ Displaystyle \ Z_ {R} = R}
В этом случае формы сигналов напряжения и тока пропорциональны и синфазны.
Индуктор и конденсатор
Идеальные катушки индуктивности и конденсаторы имеют чисто мнимое реактивное сопротивление :
сопротивление катушек индуктивности увеличивается с увеличением частоты;
- Z L знак равно j ω L {\ displaystyle \ Z_ {L} = j \ omega L}
сопротивление конденсаторов уменьшается с увеличением частоты;
- Z C знак равно 1 j ω C {\ displaystyle \ Z_ {C} = {\ frac {1} {j \ omega C}}}
В обоих случаях для приложенного синусоидального напряжения результирующий ток также является синусоидальным, но в квадратуре , сдвинутой по фазе на 90 градусов с напряжением. {j \ left (- {\ frac {\ pi} {2}} \ right)} \ end {align}}}
{j \ left (- {\ frac {\ pi} {2}} \ right)} \ end {align}}}
Величина показывает изменение амплитуды напряжения для данной амплитуды тока через импеданс, тогда как экспоненциальные множители дают фазовое соотношение.
Получение импеданса конкретного устройства
Ниже приводится расчет импеданса для каждого из трех основных элементов схемы : резистора, конденсатора и катушки индуктивности. Хотя идея может быть расширена для определения взаимосвязи между напряжением и током любого произвольного сигнала , эти производные предполагают синусоидальные сигналы. Фактически, это применимо к любым произвольным периодическим сигналам, потому что они могут быть аппроксимированы как сумма синусоид с помощью анализа Фурье .
Резистор
Для резистора существует соотношение
- v р ( т ) знак равно я р ( т ) р {\ displaystyle v _ {\ text {R}} \ left (t \ right) = {я _ {\ text {R}} \ left (t \ right)} R}
что является законом Ома .
Считая сигнал напряжения
- v р ( т ) знак равно V п грех ( ω т ) {\ Displaystyle v _ {\ текст {R}} (t) = V_ {p} \ sin (\ omega t)}
это следует из того
- v р ( т ) я р ( т ) знак равно V п грех ( ω т ) я п грех ( ω т ) знак равно р {\ displaystyle {\ frac {v _ {\ text {R}} \ left (t \ right)} {i _ {\ text {R}} \ left (t \ right)}} = {\ frac {V_ {p} \ sin (\ omega t)} {I_ {p} \ sin \ left (\ omega t \ right)}} = R}
Это говорит о том, что отношение амплитуды переменного напряжения к амплитуде переменного тока на резисторе равно , и что переменное напряжение опережает ток через резистор на 0 градусов. р {\ displaystyle R}
Этот результат обычно выражается как
- Z резистор знак равно р {\ Displaystyle Z _ {\ текст {резистор}} = R}
Конденсатор
Для конденсатора существует соотношение:
- я C ( т ) знак равно C d v C ( т ) d т {\ displaystyle i _ {\ text {C}} (t) = C {\ frac {\ operatorname {d} v _ {\ text {C}} (t)} {\ operatorname {d} t}}}
Считая сигнал напряжения
- v C ( т ) знак равно V п е j ω т {\ displaystyle v _ {\ text {C}} (t) = V_ {p} e ^ {j \ omega t} \,}
это следует из того
- d v C ( т ) d т знак равно j ω V п е j ω т {\ displaystyle {\ frac {\ operatorname {d} v _ {\ text {C}} (t)} {\ operatorname {d} t}} = j \ omega V_ {p} e ^ {j \ omega t}}
и таким образом, как и раньше,
- Z конденсатор знак равно v C ( т ) я C ( т ) знак равно 1 j ω C .
 {j \ omega t} + {\ text {Const}} = {1 \ over j \ omega C} i_ {C} (t) + {\ text {Const}}.}
{j \ omega t} + {\ text {Const}} = {1 \ over j \ omega C} i_ {C} (t) + {\ text {Const}}.}
Const член представляет собой фиксированный потенциал смещения накладывается синусоидальной потенциал переменного тока, который не играет никакой роли в анализе переменного тока. С этой целью этот член можно принять равным 0, следовательно, сопротивление
- Z конденсатор знак равно 1 j ω C . {\ displaystyle Z _ {\ text {конденсатор}} = {1 \ over j \ omega C}.}
Катушка индуктивности
Для индуктора имеем соотношение (из закона Фарадея ):
- v L ( т ) знак равно L d я L ( т ) d т {\ displaystyle v _ {\ text {L}} (t) = L {\ frac {\ operatorname {d} i _ {\ text {L}} (t)} {\ operatorname {d} t}}}
На этот раз, учитывая, что текущий сигнал:
- я L ( т ) знак равно я п грех ( ω т ) {\ Displaystyle я _ {\ текст {L}} (т) = I_ {р} \ грех (\ омега т)}
это следует из того:
- d я L ( т ) d т знак равно ω я п потому что ( ω т ) {\ displaystyle {\ frac {\ operatorname {d} i _ {\ text {L}} (t)} {\ operatorname {d} t}} = \ omega I_ {p} \ cos \ left (\ omega t \ right )}
Этот результат обычно выражается в полярной форме как
- Z катушка индуктивности знак равно ω L е j π 2 {\ displaystyle \ Z _ {\ text {индуктор}} = \ omega Le ^ {j {\ frac {\ pi} {2}}}}
или, используя формулу Эйлера, как
- Z катушка индуктивности знак равно j ω L {\ displaystyle \ Z _ {\ text {индуктор}} = j \ omega L}
Как и в случае с конденсаторами, эту формулу также можно вывести непосредственно из комплексных представлений напряжений и токов или допуская синусоидальное напряжение между двумя полюсами катушки индуктивности. В этом последнем случае интегрирования дифференциального уравнения выше , приводит к Const перспективе для тока, который представляет собой фиксированное смещение постоянного тока , протекающего через катушку индуктивности. Он установлен на ноль, потому что анализ переменного тока с использованием импеданса в частотной области учитывает одну частоту за раз, а постоянный ток представляет собой отдельную частоту в ноль герц в этом контексте.
В этом последнем случае интегрирования дифференциального уравнения выше , приводит к Const перспективе для тока, который представляет собой фиксированное смещение постоянного тока , протекающего через катушку индуктивности. Он установлен на ноль, потому что анализ переменного тока с использованием импеданса в частотной области учитывает одну частоту за раз, а постоянный ток представляет собой отдельную частоту в ноль герц в этом контексте.
Обобщенный импеданс в s-плоскости
Импеданс, определенный в терминах jω, может строго применяться только к цепям, которые управляются установившимся сигналом переменного тока. Понятие импеданса может быть расширено до цепи, запитанной любым произвольным сигналом, путем использования комплексной частоты вместо jω . Комплексная частота обозначается символом s и, как правило, является комплексным числом. Сигналы выражаются в терминах комплексной частоты с помощью преобразования Лапласа для выражения сигнала во временной области . {2}}} \\\ theta & = \ arctan {\ left ({\ frac {X} {R}} \ right)} \ end {align}}}
{2}}} \\\ theta & = \ arctan {\ left ({\ frac {X} {R}} \ right)} \ end {align}}}
Во многих приложениях относительная фаза напряжения и тока не является критичной, поэтому важна только величина импеданса.
Сопротивление
Сопротивление — это реальная часть импеданса; устройство с чисто резистивным импедансом не демонстрирует сдвига фаз между напряжением и током. р {\ displaystyle R}
- р знак равно | Z | потому что θ {\ Displaystyle \ R = | Z | \ соз {\ theta} \ quad}
Реактивность
Реактивное сопротивление — это мнимая часть импеданса; компонент с конечным реактивным сопротивлением вызывает фазовый сдвиг между напряжением на нем и током через него. Икс {\ displaystyle X} θ {\ displaystyle \ theta}
- Икс знак равно | Z | грех θ {\ Displaystyle \ X = | Z | \ грех {\ theta} \ quad}
Чисто реактивный компонент отличается тем, что синусоидальное напряжение на компоненте находится в квадратуре с синусоидальным током, проходящим через компонент. {- 1} \ quad}
{- 1} \ quad}
Знак минус указывает на то, что мнимая часть импеданса отрицательна.
На низких частотах конденсатор приближается к разомкнутой цепи, поэтому через него не течет ток.
Напряжение постоянного тока, приложенное к конденсатору, вызывает накопление заряда на одной стороне; электрическое поле за счет накопленного заряда является источником оппозиции к току. Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток стремится к нулю.
Приведенный в действие источником переменного тока, конденсатор накапливает только ограниченный заряд, прежде чем разность потенциалов изменит знак и заряд рассеется. Чем выше частота, тем меньше накапливается заряда и меньше противодействие току.
Индуктивное реактивное сопротивление
Индуктивное сопротивление является пропорционально к сигнальной частоте и индуктивности . Икс L {\ displaystyle X_ {L}} ж {\ displaystyle f} L {\ displaystyle L}
- Икс L знак равно ω L знак равно 2 π ж L {\ Displaystyle X_ {L} = \ омега L = 2 \ pi fL \ quad}
Индуктор состоит из спирального проводника.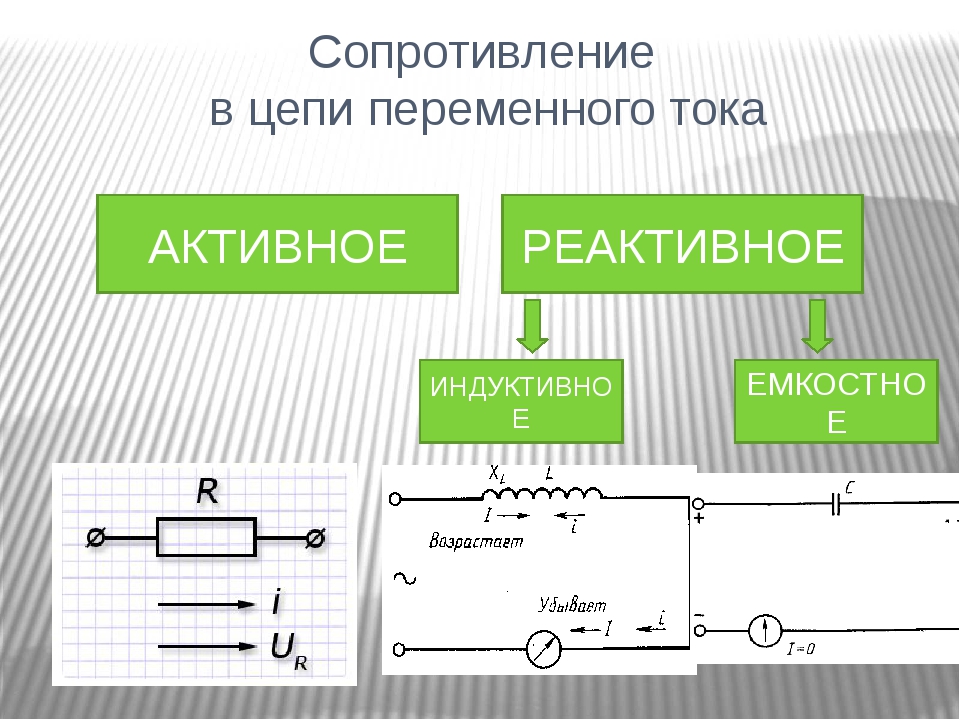 Закон электромагнитной индукции Фарадея дает обратную ЭДС (напряжение, противоположное току) из-за скорости изменения плотности магнитного потока через токовую петлю.
E {\ displaystyle {\ mathcal {E}}} B {\ displaystyle B}
Закон электромагнитной индукции Фарадея дает обратную ЭДС (напряжение, противоположное току) из-за скорости изменения плотности магнитного потока через токовую петлю.
E {\ displaystyle {\ mathcal {E}}} B {\ displaystyle B}
- E знак равно — d Φ B d т {\ displaystyle {\ mathcal {E}} = — {{d \ Phi _ {B}} \ over dt} \ quad}
Для индуктора, состоящего из катушки с петлями, это дает: N {\ displaystyle N}
- E знак равно — N d Φ B d т {\ displaystyle {\ mathcal {E}} = — N {d \ Phi _ {B} \ over dt} \ quad}
Обратная ЭДС является источником противодействия току. Постоянный постоянный ток имеет нулевую скорость изменения и рассматривает индуктор как короткое замыкание (обычно он изготовлен из материала с низким удельным сопротивлением ). Переменный ток имеет по скорости изменения усредненных по времени, которое пропорционально частоте, это приводит к увеличению индуктивного сопротивления с частотой.
Полное реактивное сопротивление
Полное реактивное сопротивление определяется как
- Икс знак равно Икс L + Икс C {\ displaystyle {X = X_ {L} + X_ {C}}} (обратите внимание, что это отрицательно) Икс C {\ Displaystyle X_ {C}}
так что полный импеданс
- Z знак равно р + j Икс {\ Displaystyle \ Z = R + jX}
Комбинирование импедансов
Общий импеданс многих простых сетей компонентов может быть рассчитан с использованием правил объединения импедансов последовательно и параллельно. Правила идентичны правилам комбинирования сопротивлений, за исключением того, что числа обычно являются комплексными . Однако в общем случае требуются эквивалентные преобразования импеданса в дополнение к последовательному и параллельному.
Комбинация серий
Для компонентов, соединенных последовательно, ток через каждый элемент схемы одинаков; полный импеданс — это сумма импедансов компонентов.
- Z экв знак равно Z 1 + Z 2 + ⋯ + Z п {\ displaystyle \ Z _ {\ text {eq}} = Z_ {1} + Z_ {2} + \ cdots + Z_ {n} \ quad}
Или явно в реальном и воображаемом выражении:
- Z экв знак равно р + j Икс знак равно ( р 1 + р 2 + ⋯ + р п ) + j ( Икс 1 + Икс 2 + ⋯ + Икс п ) {\ displaystyle \ Z _ {\ text {eq}} = R + jX = (R_ {1} + R_ {2} + \ cdots + R_ {n}) + j (X_ {1} + X_ {2} + \ cdots + X_ {n}) \ quad}
Параллельная комбинация
Для компонентов, соединенных параллельно, напряжение на каждом элементе схемы одинаковое; отношение токов, протекающих через любые два элемента, является обратной величиной их импедансов.
Следовательно, обратный полный импеданс является суммой обратных импедансов компонентов:
- 1 Z экв знак равно 1 Z 1 + 1 Z 2 + ⋯ + 1 Z п {\ displaystyle {\ frac {1} {Z _ {\ text {eq}}}} = {\ frac {1} {Z_ {1}}} + {\ frac {1} {Z_ {2}}} + \ cdots + {\ frac {1} {Z_ {n}}}}
или, когда n = 2:
- 1 Z экв знак равно 1 Z 1 + 1 Z 2 знак равно Z 1 + Z 2 Z 1 Z 2 {\ displaystyle {\ frac {1} {Z _ {\ text {eq}}}} = {\ frac {1} {Z_ {1}}} + {\ frac {1} {Z_ {2}}} = { \ frac {Z_ {1} + Z_ {2}} {Z_ {1} Z_ {2}}}}
- Z экв знак равно Z 1 Z 2 Z 1 + Z 2 {\ displaystyle \ Z _ {\ text {eq}} = {\ frac {Z_ {1} Z_ {2}} {Z_ {1} + Z_ {2}}}}
Эквивалентный импеданс можно рассчитать как эквивалентное последовательное сопротивление и реактивное сопротивление .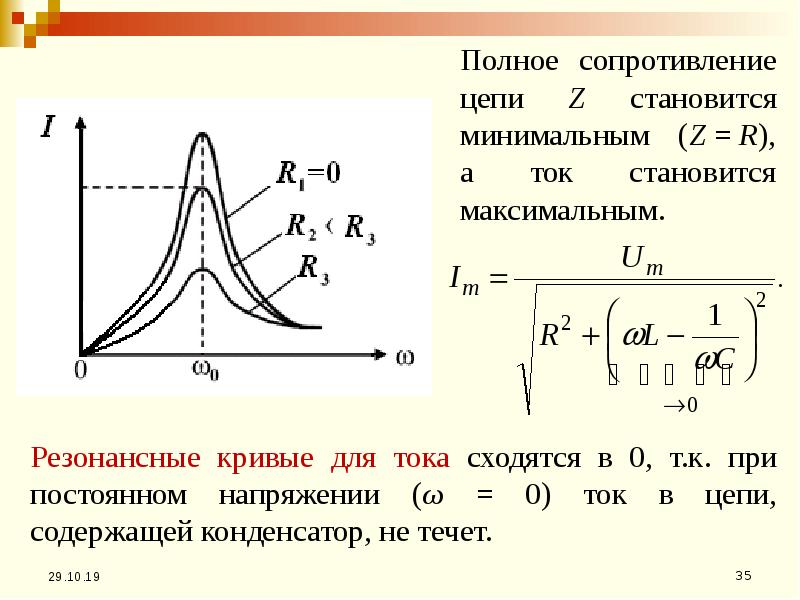 {2}}} \ end {align}}}
{2}}} \ end {align}}}
Измерение
Измерение импеданса устройств и линий передачи — практическая задача в радиотехнике и других областях. Измерения импеданса можно проводить на одной частоте, или может представлять интерес изменение импеданса устройства в диапазоне частот. Импеданс может быть измерен или отображен непосредственно в омах, или могут отображаться другие значения, относящиеся к импедансу; например, в радиоантенне коэффициент стоячей волны или коэффициент отражения могут быть более полезными, чем только импеданс. Измерение импеданса требует измерения величины напряжения и тока, а также разности фаз между ними. Импеданс часто измеряется «мостовыми» методами , подобными мосту Уитстона постоянного тока ; калиброванный эталонный импеданс регулируется для компенсации влияния импеданса тестируемого устройства. Измерение импеданса в силовых электронных устройствах может потребовать одновременного измерения и подачи питания на работающее устройство.
Импеданс устройства можно рассчитать сложным делением напряжения и тока. Импеданс устройства можно рассчитать, приложив к устройству синусоидальное напряжение последовательно с резистором и измерив напряжение на резисторе и на устройстве. Выполнение этого измерения путем качания частот подаваемого сигнала позволяет получить фазу и величину импеданса.
Использование импульсной характеристики может использоваться в сочетании с быстрым преобразованием Фурье (БПФ) для быстрого измерения электрического импеданса различных электрических устройств.
Измеритель иммитанса (Индуктивность (L), емкости (С) и сопротивление (R)) , представляет собой устройство , обычно используется для измерения индуктивности, сопротивления и емкости компонента; исходя из этих значений, можно рассчитать импеданс на любой частоте.
пример
Рассмотрим контур резервуара LC . Комплексный импеданс цепи равен
- Z ( ω ) знак равно j ω L 1 — ω 2 L C .
 {2} LC = 1.}
{2} LC = 1.}
Следовательно, угловая частота основного резонанса равна
- ω знак равно 1 L C . {\ displaystyle \ omega = {1 \ over {\ sqrt {LC}}}.}
Переменный импеданс
В общем, ни импеданс, ни адмитанс не могут изменяться со временем, поскольку они определены для комплексных экспонент, в которых -∞ < t <+ ∞ . Если комплексное экспоненциальное отношение напряжения к току изменяется во времени или по амплитуде, элемент схемы не может быть описан с использованием частотной области. Однако многие компоненты и системы (например, варикапы , которые используются в радиотюнерах ) могут демонстрировать нелинейные или изменяющиеся во времени отношения напряжения к току, которые кажутся линейно-инвариантными во времени (LTI) для слабых сигналов и для небольших окон наблюдения. так что их можно грубо описать как если бы они имели изменяющийся во времени импеданс. Это описание является приблизительным: при больших колебаниях сигнала или широких окнах наблюдения зависимость напряжения от тока не будет LTI и не может быть описана импедансом.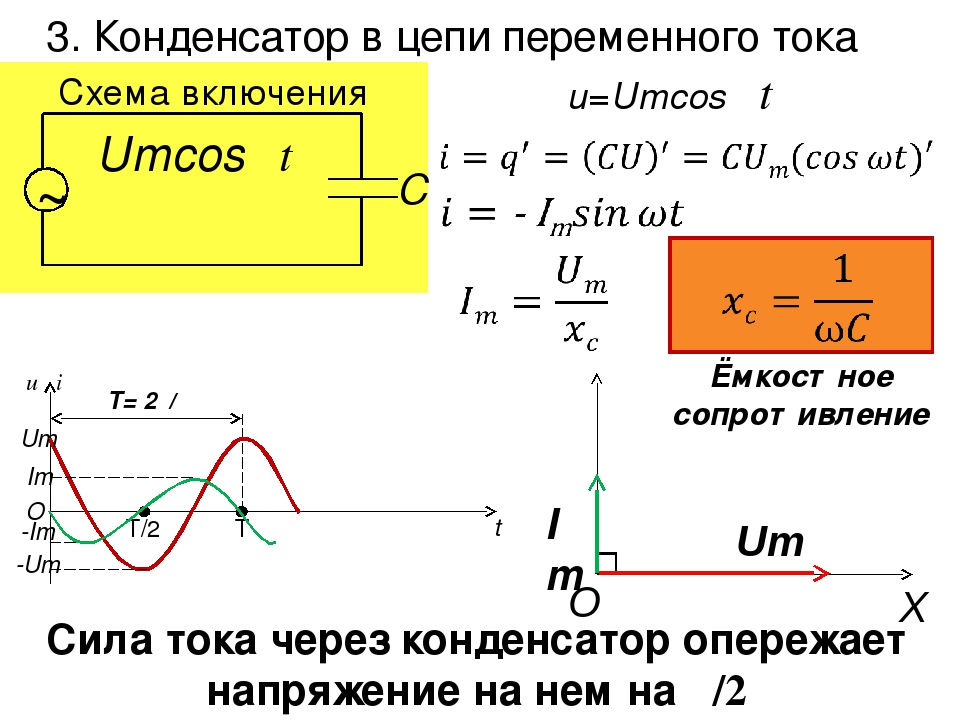
Смотрите также
Рекомендации
внешние ссылки
Электрический ток (стр. 2 из 2)
Условия идеальности цепи:
· Ёмкость конденсатора не равна нулю, а его активное сопротивление и индуктивность равны нулю. С ¹ 0, RС= 0, LC = 0.
Особенности цепи с ёмкостью:
1. Соблюдается закон Ома.2. Ёмкость оказывает переменному току сопротивление, которое называется ёмкостным. Оно обозначается Xс и уменьшается с увеличением частоты не линейно.
3.В цепи есть сдвиг фаз между напряжением и током: V отстает от I по фазе на угол p/2
4.Ёмкостное сопротивление не потребляет энергии, т.к. она запасается в электрическом поле конденсатора, а затем отдается в электрическую цепь. Поэтому ёмкостное сопротивление называется кажущимся или мнимым.
3.Полная цепь переменного тока и её виды. Импеданс и его формула. Особенности импеданса живой ткани.
Полная цепь переменного тока — это цепь из генератора, а также R, C, и L элементов, взятых в разных сочетаниях и количествах.
Для разбора проходящих в электрических цепях процессов используют полные последовательные и параллельные цепи.
Последовательная цепь — это такая цепь, где все элементы могут быть соединены последовательно, один за другим.
В параллельной цепи R, C, L элементы соединены параллельно.
Особенности полной цепи:
1.Соблюдается закон Ома
2.Полная цепь оказывает переменному току сопротивление. Это сопротивление называется полным (мнимым, кажущимся) или импедансом.
3.Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и вычисляется не простым, а геометрическим (векторным) суммированием. Для последовательно соединенных элементов формула импеданса имеет следующее значение:
здесь:
Z — импеданс последовательной цепи,
R — активное сопротивление,
XL– индуктивное и XC – ёмкостное сопротивление,
L — индуктивность катушки (генри),
C — ёмкость конденсатора (фарад).
Так как ёмкостное и индуктивное сопротивления дают для напряжения сдвиг фаз в противоположном направлении, возможен случай, когда XL = XC. При этом алгебраическая сумма модулей будет равна нулю, а импеданс – наименьшим.
Состояние, при котором в цепи переменного тока ёмкостное сопротивление равно индуктивному, называется резонансом напряжения. Частота, при которой XL = XC, называется резонансной частотой. Эту частоту np можно определить по формуле Томсона:
4.Особенности импеданса живой ткани и её эквивалентная электрическая схема.
При пропускании тока через живую ткань, её можно рассматривать как электрическую цепь, состоящую из определенных элементов.
Экспериментально установлено, что это цепь обладает свойствами активного сопротивления и ёмкости. Это доказывается выделением тепла и уменьшением полного сопротивления ткани с возрастанием частоты. Свойств индуктивности у живой ткани практически не обнаруживается. Таким образом, живая ткань представляет собой сложную, но не полную электрическую цепь.
Таким образом, живая ткань представляет собой сложную, но не полную электрическую цепь.
Импеданс живой ткани можно рассматривать как для последовательного, так и для параллельного соединения её элементов.
При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:
Z_ — импеданс последовательной цепи,
R — её активное сопротивление,
XC — ёмкостное сопротивление.
При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:
Теоретические формулы импеданса живой ткани при параллельном и последовательном соединении её элементов от экспериментальных отличаются следующим:
1.При последовательной схеме соединения практические данные дают большие отклонения на низких частотах.
2.При параллельной схеме эти измерения показывают конечное значение Z, хотя теоретически оно должно стремиться к нулю.
Эквивалентная электрическая схема живой ткани – это условная модель, приближенно характеризующаяживую ткань, как проводник переменного тока.
Схема позволяет судить:
1.Какими электрическими элементами обладает ткань
2.Как соединены эти элементы.
3.Как будут меняться свойства ткани при изменении частоты тока.
В основе схемы лежат три положения:
1.Внеклеточная среда и содержимое клетки есть ионные проводники с активным сопротивлением среды Rср и клетки Rк.
2.Клеточная мембрана есть диэлектрик, но не идеальный, а с небольшой ионной проводимостью, а, следовательно, и сопротивлением мембраны Rм.
3.Внеклеточная среда и содержимое клетки, разделённые мембраной, являются конденсаторами См определенной ёмкости (0,1 – 3,0 мкФ/см2).
Если в качестве модели живой ткани взять жидкую тканевую среду – кровь, содержащую только эритроциты, то при составлении эквивалентной схемы нужно учитывать пути электрического тока.
Их два:
1.В обход клетки, через внеклеточную среду.
2.Через клетку.
Путь в обход клетки представлен только сопротивлением средыRср.
Путь через клетку сопротивлением содержимого клетки Rк, а также сопротивлением и ёмкостью мембраны.Rм, См.
Если заменить электрические характеристики соответствующими обозначениями, то получим эквивалентные схемы разной степени точности:
Схема Фрике (ионная проводимость не
учитывается).
Схема Швана (ионная проводимость учитывается в виде сопротивления мембраны)
Обозначения на схеме:
Rcp — активное сопротивление клеточной среды
Rk — Сопротивление клеточного содержимого
Cm — ёмкость мембраны
Rm — сопротивление мембраны.
Анализ схемы показывает, что при увеличении частоты тока проводимость клеточных мембран увеличивается, а полное сопротивление тканевой среды уменьшается, что соответствует практически проведенным измерениям.
5. Живая ткань как проводник переменного электрического тока. Дисперсия электропроводности и её количественная оценка.
Дисперсия электропроводности и её количественная оценка.
Экспериментально установлены следующие особенности живой ткани как проводника переменного ток:
1. Сопротивление живой ткани переменном току меньше, чем постоянному.
2. Электрические характеристики ткани зависят как от её вида, так и от частоты тока.
3. С увеличением частоты полное сопротивление живой ткани нелинейно уменьшается до определенного значения, а затем остаётся практически постоянным (в большинстве на частотах свыше 106 Гц)
4. На определенной частоте полное сопротивление зависит также от физиологического состояния (кровенаполнения), что используется на практике. Исследование периферического кровообращения на основе измерения электрического сопротивления называются реография (импедансплетизмография).
5. При умирании живой ткани её сопротивление уменьшается и от частоты не зависит.
6. При прохождении переменного тока через живые ткани наблюдается явление, которое называется дисперсией электропроводности.
Графики такой зависимости называют дисперсионными кривыми. Дисперсионные кривые строят в прямоугольной системе координат, где по вертикали откладывают значения полного (Z) или удельного сопротивления, а по горизонтали — частоту в логарифмическом масштабе (Lgn).
Частотные зависимости по форме кривой для разных тканей сходный, но отличается значением сопротивления.
Имеется несколько диапазонов частот, на которых дисперсия особенно выражена. Один из них соответствует интервалу 102 -106 Гц
Особенности дисперсии:
1. Присуща только живым тканям.
2. Более выражена на частотах до 1 МГц.
3. На практике используется для оценки физиологического состояния и жизнеспособности тканей.
Количественно оценка дисперсии проводиться по коэффициенту дисперсии (К).
Коэффициент дисперсии это безразмерная величина, равная отношению низкочастотного (102) полного (или удельного) сопротивления к высокочастотному (106 Гц).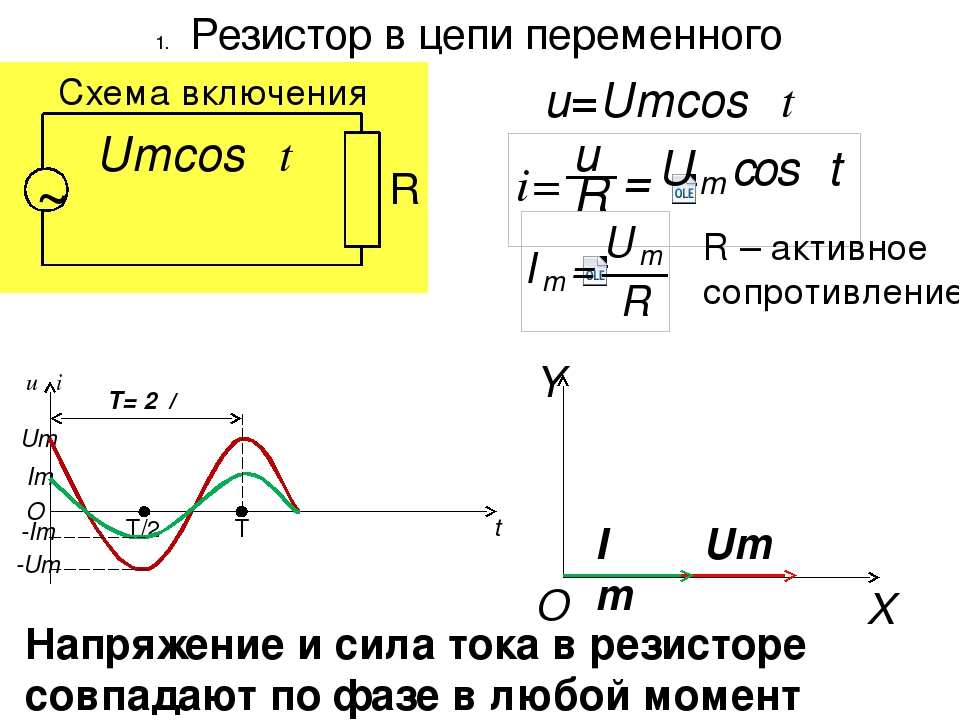
Z1 – полное сопротивление на частоте 102Гц
Z2 – полное сопротивление на частоте 106 Гц
r1, r2 — удельное сопротивление на этих частотах
Значение коэффициента дисперсии зависит от вида ткани, её физиологического состояния, эволюционной стадии развития животного. Например, для печени животного К = 9 -10 единиц, а для печени лягушки 2 -3 единицы. При умирании ткани коэффициент дисперсии стремиться к единице.
Явление дисперсии связывают с наличием в живых тканях поляризации, которая с увеличением частоты меньше влияет на полное сопротивление. Поэтому коэффициент дисперсии часто называют коэффициентом поляризации.
Кроме частотных зависимостей в живых тканях отмечаются фазовые сдвиги между током и напряжением, которые тоже, но в меньшей степени, зависят от частоты.
Фазовые сдвиги тоже уменьшаются при умирании тканей и, в перспективе, могут быть использованы для практических целей.
• Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц
Этот калькулятор импеданса последовательной RC-цепи определяет импеданс и угол разности фаз конденсатора и резистора, соединенных последовательно для заданной частоты синусоидального сигнала.
Пример: Рассчитайте полное сопротивление конденсатора 500 мкФ и резистора 0,2 Ом на частоте 25 кГц.
Вход
Сопротивление, R
миллиом (мОм) Ом (Ом) килоом (кОм) мегом (МОм)
Емкость, C
фарад (F) микрофарад (мкФ, мкФ) нанофара (пФ)
Частота, f
герц (Гц) миллигерц (МГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)
Выход
Угловая частота ω
=рад / с X C = Ом
Общее сопротивление RC | Z RC | = Ом
Разность фаз φ = ° = рад
Введите значения сопротивления, емкости и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Calculate . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Для расчета используются следующие формулы:
где
Z RC — сопротивление RC-цепи в Ом (Ом),
ω = 2πf — угловая частота в рад / с,
f — частота в герцах (Гц),
R — сопротивление в омах (Ом),
C — емкость в фарадах (F),
φ — это разность фаз между полным напряжением V T и полным током I T в градусах (°) и радианах, а
j — мнимая единица.
Для расчета введите емкость, сопротивление и частоту, выберите единицы измерения, и результат для импеданса RC будет показан в омах, а для разности фаз в градусах. Также будет рассчитано реактивное сопротивление конденсатора.
График импеданса последовательной RC-цепи Z RC от частоты f для данной емкости и сопротивления показывает обратную пропорциональность частоте
Векторная диаграмма для последовательной RC-цепи показывает, что волна полного тока опережает волна полного напряжения.Угол поворота составляет менее 90 ° и более 0 °. Под углом 90 ° устанавливается перемычка вместо резистора (схема чисто емкостная), а при 0 ° перемычка устанавливается вместо конденсатора (схема чисто резистивная)
Состоит простая последовательная RC-цепочка или схема резистор-конденсатор резистора и конденсатора, соединенных последовательно и управляемых источником напряжения. Ток в конденсаторе и резисторе одинаков, потому что они соединены последовательно. Напряжения на резисторе V R и конденсаторе V C показаны на схеме под прямым углом друг к другу.Их сумма всегда больше, чем полное напряжение V T .
Если вы посмотрите на уравнение для расчета импеданса (см. Выше), вы заметите, что оно похоже на уравнение для расчета гипотенузы прямоугольного треугольника. Это связано с тем, что импеданс RC-цепи в графической форме выглядит так, как на этом рисунке, где сопротивление R находится на горизонтальной оси, а реактивное сопротивление X C — на вертикальной оси. Гипотенуза — это импеданс цепи, а фазовый угол — это угол между горизонтальной осью и вектором импеданса.
Выше), вы заметите, что оно похоже на уравнение для расчета гипотенузы прямоугольного треугольника. Это связано с тем, что импеданс RC-цепи в графической форме выглядит так, как на этом рисунке, где сопротивление R находится на горизонтальной оси, а реактивное сопротивление X C — на вертикальной оси. Гипотенуза — это импеданс цепи, а фазовый угол — это угол между горизонтальной осью и вектором импеданса.
Фазовый угол может составлять от 0 ° для чисто резистивной цепи до –90 ° для чисто емкостной цепи. Из треугольника реактивного сопротивления
или с помощью функции арктангенса (арктангенса)
В последовательной RC-цепи с источником синусоидального напряжения волна тока опережает волну напряжения с запаздыванием менее 90 ° (нулевое сопротивление) и более 0 ° (нулевая емкость). Другими словами, напряжение отстает от тока на φ по фазе; 0 ° ≤ φ ≤ 90 °.Если напряжение В равно В = В м sin (2πft) , то ток I равен I = I м sin (2πft — φ) , где V м и I м. — амплитуды напряжения и тока, f — частота (постоянная), φ — фазовый угол (постоянная) и t — время (переменная)
— амплитуды напряжения и тока, f — частота (постоянная), φ — фазовый угол (постоянная) и t — время (переменная)
В последовательной RC-цепи тот же ток I протекает как через конденсатор, так и через резистор. Напряжение конденсатора V C отстает от общего тока на 90 °, а напряжение резистора синфазно с общим током.Согласно закону напряжения Кирхгофа сумма падений напряжения должна равняться общему напряжению V T . Напряжения резистора и конденсатора V R и V C не совпадают по фазе на 90 ° друг с другом, поэтому они должны быть добавлены как векторные величины, а общее напряжение V T определяется как
. напряжение всегда меньше суммы напряжений на резисторе и конденсаторе — точно так же, как в любом прямоугольном треугольнике, где длина гипотенузы короче суммы двух катетов треугольника.
Режимы отказа
Что делать, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные режимы
Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:
Различные режимы постоянного тока
Короткое замыкание
Обрыв цепи
Чисто емкостная схема
Примечания
- В наших объяснениях поведения этой схемы нулевая частота означает постоянный ток.
 Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения. - При нулевой частоте мы считаем реактивное сопротивление конденсатора равным нулю, если его емкость бесконечно велика. Если конденсатор имеет конечную емкость, его реактивное сопротивление при нулевой частоте бесконечно велико и для источника постоянного напряжения оно представляет собой разомкнутую цепь или, другими словами, удаленный конденсатор.
Калькулятор импеданса параллельной цепи RL • Калькуляторы электрических, радиочастот и электроники • Онлайн-преобразователи единиц
Этот калькулятор импеданса параллельной цепи RL определяет импеданс и угол разности фаз индуктора и резистора, подключенных параллельно для заданной частоты синусоидальный сигнал.Также определяется угловая частота.
Пример: Рассчитайте полное сопротивление катушки индуктивности 500 мГн и резистора 200 кОм на частоте 25 кГц.
Вход
Сопротивление, R
миллиом (мОм) Ом (Ом) килоом (кОм) мегом (МОм)
Индуктивность, л
генри (H) миллигенри (мГн) микрогенри (мкГн) ) пикогенри (pH)
Частота, f
герц (Гц) миллигерц (МГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)
Выход
Угловая частота с
рад Индуктивное реактивное сопротивление X L = ОмОбщее сопротивление RL | Z RL | = Ом
Разность фаз φ = ° = рад
Введите значения сопротивления, индуктивности и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Calculate . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Для расчета используются следующие формулы:
где
На векторной диаграмме для параллельной цепи RL видно, что волна полного тока отстает от волны полного напряжения .Запаздывание меньше 90 ° и больше 0 °. При 90 ° резистор удаляется из цепи (цепь чисто индуктивная), а при 0 ° индуктор удаляется из цепи (цепь чисто резистивная)
Z RL — полное сопротивление цепи RL в Ом (Ом),
ω = 2πf — угловая частота в рад / с,
f — частота в герцах (Гц),
R — сопротивление в Ом (Ом),
L — индуктивность в генри (Гн),
φ — фазовый сдвиг между полным напряжением В T и полным током I T в градусах (°) и радианах, и
j — мнимая единица.
Для расчета введите индуктивность, сопротивление и частоту, выберите единицы измерения, и результат для импеданса RL будет показан в омах, а для разности фаз — в градусах и радианах. Также будет рассчитано индуктивное реактивное сопротивление в омах.
График импеданса параллельной цепи RL Z RL в зависимости от частоты f для заданных индуктивности и сопротивления
Для параллельной цепи RL импеданс представляет собой комплексное число и определяется как
Приложенное напряжение В, T одинаково как для резистора, так и для катушки индуктивности.Общий ток I T делится на два тока ответвления: I L и I R :
Согласно действующему закону Кирхгофа, общий ток I T — это сумма векторов двух токов ответвления I L и I R , которые не совпадают по фазе на 90 °. Следовательно,
Следовательно,
Режимы отказа
Что, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные режимы
Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:
Различные режимы постоянного тока
Короткое замыкание
Обрыв цепи
Чисто индуктивная цепь
Индуктивная цепь
Примечания
- В наших объяснениях поведения этой цепи нулевая частота означает постоянный ток.Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
- При нулевой частоте мы считаем реактивное сопротивление идеальной катушки индуктивности бесконечно большим, если ее индуктивность бесконечно велика. Если катушка индуктивности имеет конечную индуктивность, ее реактивное сопротивление при нулевой частоте равно нулю, а для источника постоянного напряжения оно представляет собой короткое замыкание.

Калькулятор последовательного сопротивления R и C
- Цель использования
- , чтобы проверить мой расчет.2
[1] 2020/05/21 01:01 Мужской / Уровень 20 лет / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- ухудшает ли мой осциллограф 20 пФ измерения при 50 Ом, 14 МГц?
[3] 21.03.2019 02:23 Мужчина / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Радиолюбитель
- Комментарий / запрос
- Нужна просто формула, но калькулятор — приятное дополнение, чтобы не допустить ошибок
[4] 2018/02/24 01:50 Женский / До 20 лет / Старшая школа / Университет / Аспирантка / Очень /
- Цель использования
- Быстрые вычисления, когда я не хочу делать их вручную
[5] 2018/01/23 10:58 Мужской / До 20 лет / Старшая школа / Университет / Аспирант / Очень /
- Цель использования
- Расчет R&C для защиты реле, активирующего индуктивное оборудование (насос)
[6] 2017/12/03 17:59 Мужчина / 60 лет и старше / Пенсионеры / Очень /
- Цель использования
- Светодиодные лампы в доме 3-х ходовая цепь светится после отключения.
 Проверка демпфера для включения параллельно осветительной арматуре.
Проверка демпфера для включения параллельно осветительной арматуре.
[7] 2017/11/24 00:51 Мужчина / 50 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Проверить программные алгоритмы серии RC.
- Комментарий / запрос
- Метод генерации значений амплитуды и фазы в заданном диапазоне частот.
[8] 2017/11/13 08:53 Мужчина / Уровень 30 лет / Инженер / Очень /
- Цель использования
- Образование
- Комментарий / запрос
- объяснения формул, или, по крайней мере, констант.
[9] 2017/11/05 19:00 Мужской / 20-летний уровень / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- Получение передаточных функций контуров ПИ
- Комментарий / запрос
- Добавить функцию для передачи функций во временной области.
Легко будет внедрить во встраиваемые усилители
[10] 31.10.2017 19:39 — / 30-летний уровень / Инженер / Полезное /
Импеданс
Импеданс
Полное сопротивление току, протекающему в цепи переменного тока, называется импедансом и обозначается буквой Z.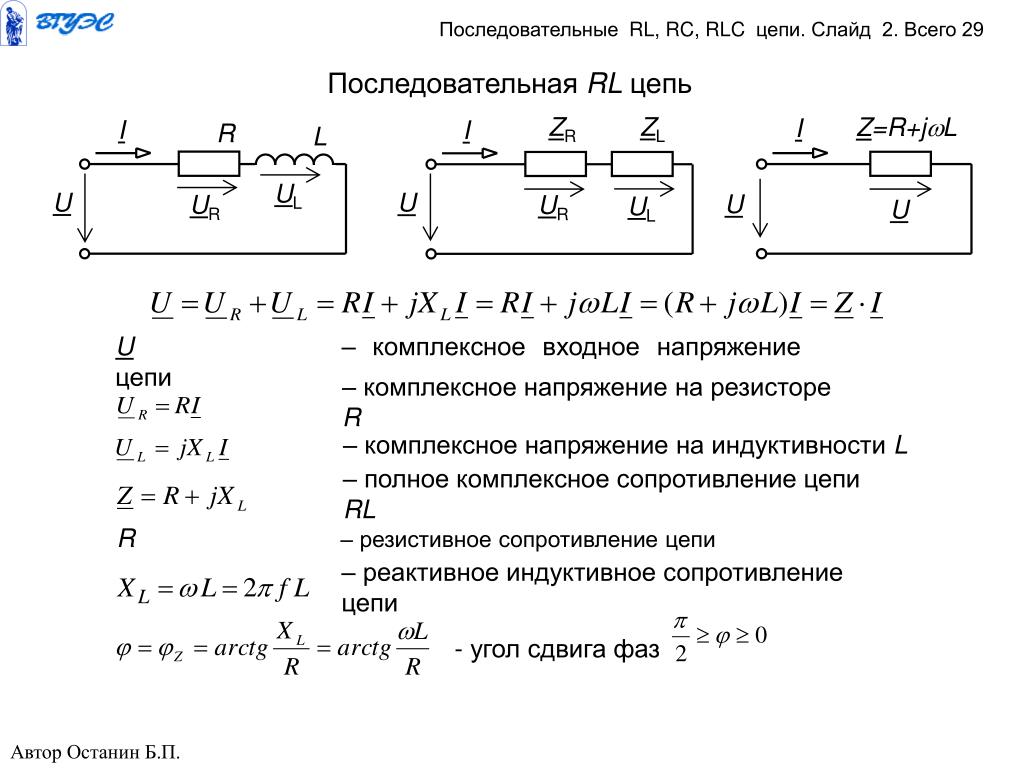 Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное сопротивление току, протекающему в цепи переменного тока). Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.
Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное сопротивление току, протекающему в цепи переменного тока). Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.
Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только в том случае, если эта цепь содержит только сопротивление, а не индуктивность или емкость.Как в последовательной, так и в параллельной цепях, если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как сопротивление, а закон Ома для цепи переменного тока, I = E / Z, точно такой же, как для цепи постоянного тока. схема. На рис. 9-22 показана последовательная схема, содержащая нагревательный элемент с сопротивлением 11 Ом, подключенный к источнику 110 В.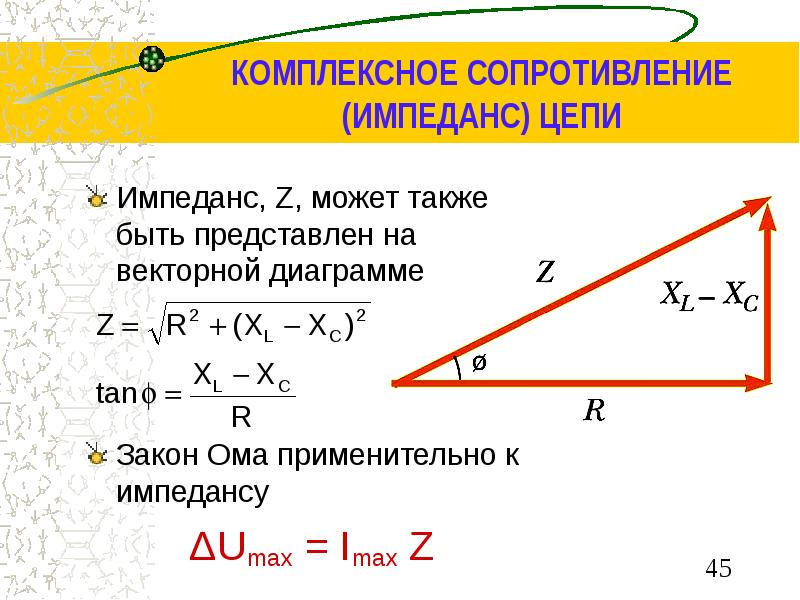 Чтобы определить, какой ток протекает при подаче переменного тока 110 В, решается следующий пример:
Чтобы определить, какой ток протекает при подаче переменного тока 110 В, решается следующий пример:
Если есть два значения сопротивления, подключенных параллельно к переменному напряжению, как показано на Рисунке 9-23, полное сопротивление равно общему сопротивлению цепи. Опять же, вычисления будут производиться так же, как если бы это была цепь постоянного тока, и применимо следующее:
Поскольку это чисто резистивная цепь R T = Z (сопротивление = импеданс)
To Определите ток в цепи, используя уравнение:
Импеданс — это полное сопротивление току в цепи переменного тока.Если цепь имеет индуктивность или емкость, необходимо учитывать сопротивление (R), индуктивное реактивное сопротивление (X L ) и / или емкостное реактивное сопротивление (X C ) для определения полного сопротивления (Z). В этом случае Z не равно R T . Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником.[Рис. 9-24] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон. Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.
В этом случае Z не равно R T . Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником.[Рис. 9-24] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон. Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.
На практике, если последовательная цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 9-25, соотношение между сторонами может быть указано как:
Квадратный корень из обеих частей уравнения дает:
Эту формулу можно использовать для определения импеданса, если известны значения индуктивного реактивного сопротивления и сопротивления. Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X C вместо X L . В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):
Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X C вместо X L . В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):
или
Пример 1 показан на рисунке 9-25.Здесь последовательная цепь, содержащая резистор и катушку индуктивности, подключена к источнику 110 вольт при 60 циклах в секунду. Резистивный элемент представляет собой простой измерительный элемент 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какое значение импеданса и тока в цепи?
Решение:
Сначала вычисляется индуктивное сопротивление катушки:
Затем вычисляется полное полное сопротивление:
Помните, что при расчетах для Z всегда используйте индуктивное реактивное сопротивление, а не индуктивность, и используйте емкостное сопротивление. , а не емкость.
, а не емкость.
После определения полного сопротивления можно рассчитать общий ток.
Поскольку эта цепь является резистивной и индуктивной, существует фазовый сдвиг там, где напряжение ведет к току.
Пример 2 представляет собой проиллюстрированную последовательную схему, в которой конденсатор емкостью 200 мкФ соединен последовательно с резистором 10 Ом. [Рисунок 9-26] Какое значение имеет импеданс, ток и падение напряжения на резисторе?
Рисунок 9-26. Цепь, содержащая сопротивление и емкость.Решение:
Сначала емкость изменяется с микрофарад на фарады. Поскольку 1 миллион микрофарад равен 1 фараду, тогда 200 мкФ = 0,000200 фарад
Далее решаем емкостное реактивное сопротивление:
Чтобы найти полное сопротивление,
Поскольку эта цепь резистивная и емкостная, существует фазовый сдвиг, при котором ток напряжение проводов:
Чтобы найти ток:
Чтобы найти падение напряжения на резисторе (E R ):
Чтобы найти падение напряжения на конденсаторе (E C ):
Сумма этих двух напряжений не равна приложенному напряжению, поскольку ток опережает напряжение.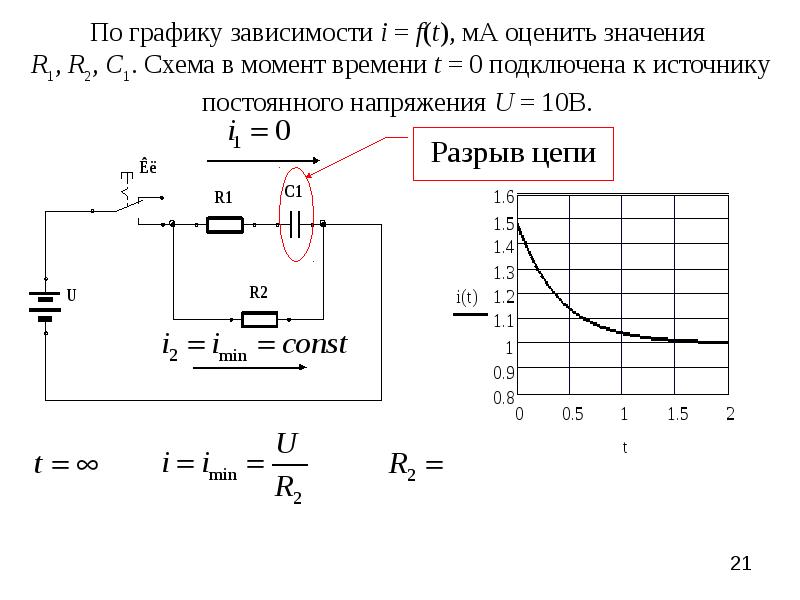 Используйте следующую формулу, чтобы найти приложенное напряжение:
Используйте следующую формулу, чтобы найти приложенное напряжение:
Если в цепи есть сопротивление, индуктивность и емкость, для определения полного сопротивления используется следующее уравнение.
Пример 3: Каково полное сопротивление последовательной цепи, состоящей из конденсатора с емкостным реактивным сопротивлением 7 Ом, катушки индуктивности с индуктивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 9-27] Рисунок 9-27. Цепь, содержащая сопротивление, индуктивность и емкость.
Решение:
Чтобы найти общий ток:
Помните, что индуктивные и емкостные реактивные сопротивления могут вызвать фазовый сдвиг между напряжением и током. В этом примере индуктивное реактивное сопротивление больше емкостного, поэтому напряжение ведет к току.
Следует отметить, что, поскольку индуктивное реактивное сопротивление, емкостное реактивное сопротивление и сопротивление влияют друг на друга под прямым углом, падения напряжения в любой последовательной цепи переменного тока следует складывать с использованием векторного сложения. На рисунке 9-28 показаны падения напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.
На рисунке 9-28 показаны падения напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.
Чтобы рассчитать отдельные падения напряжения, просто используйте уравнения:
Чтобы определить общее приложенное напряжение для цепи, каждое отдельное падение напряжения должно быть добавлено с помощью векторного сложения.
Параллельные цепи переменного тока
При решении параллельных цепей переменного тока необходимо также использовать производную теоремы Пифагора.Уравнение для определения полного сопротивления в цепи переменного тока выглядит следующим образом:
Чтобы определить полное сопротивление параллельной цепи, показанной на рисунке 9-29, сначала нужно определить емкостное и индуктивное реактивные сопротивления. (Не забудьте перевести микрофарады в фарады.)
Рисунок 9-29. Полный импеданс параллельной цепи.Затем можно найти полное сопротивление:
Для определения протекания тока в цепи:
Чтобы определить протекание тока через каждый параллельный путь цепи, вычислите I R , I L и I C .
Следует отметить, что общий ток в параллельных цепях определяется с помощью векторного сложения отдельных потоков тока следующим образом:
Мощность в цепях переменного тока
Поскольку напряжение и ток определяют мощность , есть сходства в мощности, потребляемой цепями переменного и постоянного тока. Однако в переменном токе ток зависит как от сопротивления, так и от реактивного сопротивления цепи. Мощность, потребляемая любой цепью переменного тока, является функцией приложенного напряжения, а также сопротивления и реактивного сопротивления цепи.Цепи переменного тока имеют два различных типа мощности: один создается сопротивлением цепи, а другой — реактивным сопротивлением цепи.
Истинная мощность
Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность — это мощность, потребляемая участком сопротивления цепи, и измеряется в ваттах (Вт).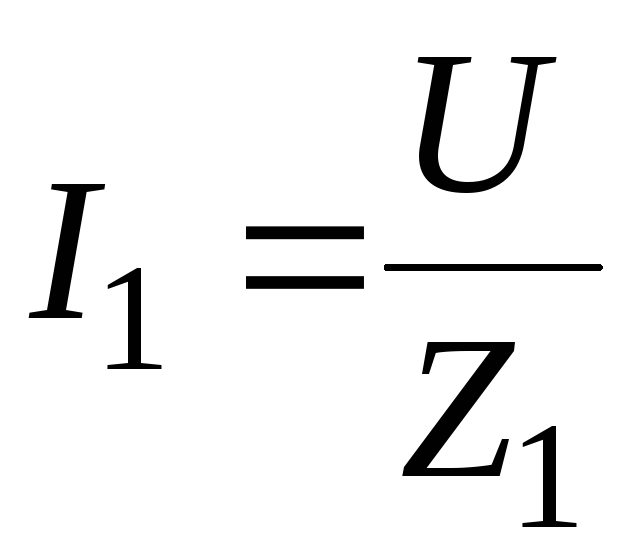 Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:
Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:
Полная мощность
Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи.Полная мощность — это мощность, потребляемая всей цепью, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Полная мощность — это произведение эффективного напряжения на эффективный ток. Полная мощность рассчитывается по формуле:
Коэффициент мощности
Как видно на Рисунке 9-30, резистивная мощность и реактивная мощность влияют на схему под прямым углом друг к другу.Коэффициент мощности в цепи переменного тока создается этим эффектом прямого угла.
Рисунок 9-30. Соотношения сил в цепи переменного тока. Коэффициент мощности можно определить как математическую разницу между истинной мощностью и полной мощностью. Коэффициент мощности (PF) — это коэффициент и всегда измеряется в диапазоне от 0 до 100. Коэффициент мощности напрямую связан с фазовым сдвигом цепи. Чем больше фазовый сдвиг цепи, тем ниже коэффициент мощности. Например, цепь переменного тока, которая является чисто индуктивной (содержит только реактивное сопротивление и не имеет сопротивления), имеет фазовый сдвиг 90 ° и коэффициент мощности 0.0. Цепь переменного тока, которая является чисто резистивной (без реактивного сопротивления), имеет фазовый сдвиг 0 и коэффициент мощности 100. Коэффициент мощности рассчитывается по следующей формуле:
Коэффициент мощности (PF) — это коэффициент и всегда измеряется в диапазоне от 0 до 100. Коэффициент мощности напрямую связан с фазовым сдвигом цепи. Чем больше фазовый сдвиг цепи, тем ниже коэффициент мощности. Например, цепь переменного тока, которая является чисто индуктивной (содержит только реактивное сопротивление и не имеет сопротивления), имеет фазовый сдвиг 90 ° и коэффициент мощности 0.0. Цепь переменного тока, которая является чисто резистивной (без реактивного сопротивления), имеет фазовый сдвиг 0 и коэффициент мощности 100. Коэффициент мощности рассчитывается по следующей формуле:
Пример расчета коэффициента мощности: Рисунок 9-31 показывает нагрузку переменного тока, подключенную к источнику питания на 50 В. Потребляемый в цепи ток составляет 5 ампер, а общее сопротивление цепи составляет 8 Ом. Определите истинную мощность, полную мощность и коэффициент мощности для этой цепи.
Рисунок 9-31. Нагрузка переменного тока подключена к источнику питания на 50 В.
Решение:
Коэффициент мощности также может быть представлен в процентах. Используя процентное соотношение для отображения коэффициента мощности, схема в предыдущем примере будет иметь коэффициент мощности 80 процентов.
Следует отметить, что низкий коэффициент мощности нежелателен. Цепи с более низким коэффициентом мощности создают избыточную нагрузку на источник питания и снижают эффективность системы. Генераторы переменного тока для самолетов обычно должны работать с коэффициентом мощности от 90 до 100 процентов.Поэтому очень важно тщательно учитывать коэффициент мощности при проектировании электрической системы самолета.
Летный механик рекомендует
Что такое электрическое сопротивление? | ОРЕЛ
Вы пытаетесь понять электрическое сопротивление? Скорее всего, если вы уже углублялись в эту тему в прошлом, то получили некоторый жаргон вроде фазоров, фазовых соотношений и даже воображаемого сопротивления. Что это вообще такое ?!
Не все из нас — инженеры-электрики с высшим образованием. Некоторые из нас просто возятся с электроникой в свободное время и никогда не сталкиваются со строгой математикой, с которой вы сталкиваетесь в университете. Но это не значит, что понимание импеданса должно быть препятствием. Если вы планируете работать с электронными устройствами с питанием от переменного тока, вам нужно знать, что такое импеданс и что он делает с вашей схемой.
Некоторые из нас просто возятся с электроникой в свободное время и никогда не сталкиваются со строгой математикой, с которой вы сталкиваетесь в университете. Но это не значит, что понимание импеданса должно быть препятствием. Если вы планируете работать с электронными устройствами с питанием от переменного тока, вам нужно знать, что такое импеданс и что он делает с вашей схемой.
Давай узнаем!
Не совсем яблоки в яблоки
Лучший способ понять электрический импеданс — это сравнить его с тем, с чем вы уже знакомы — сопротивлением.И здесь мы собираемся предложить краткое изложение импеданса в двух словах:
Электрический импеданс — это просто форма сопротивления, которая зависит от частоты.
Вот и все. Вы можете уйти прямо сейчас и добавить еще одно слово в свой словарь по электротехнике. Когда вы понижаете импеданс, он обеспечивает сопротивление току в зависимости от рабочей частоты цепи. Но, конечно, есть еще кое-что.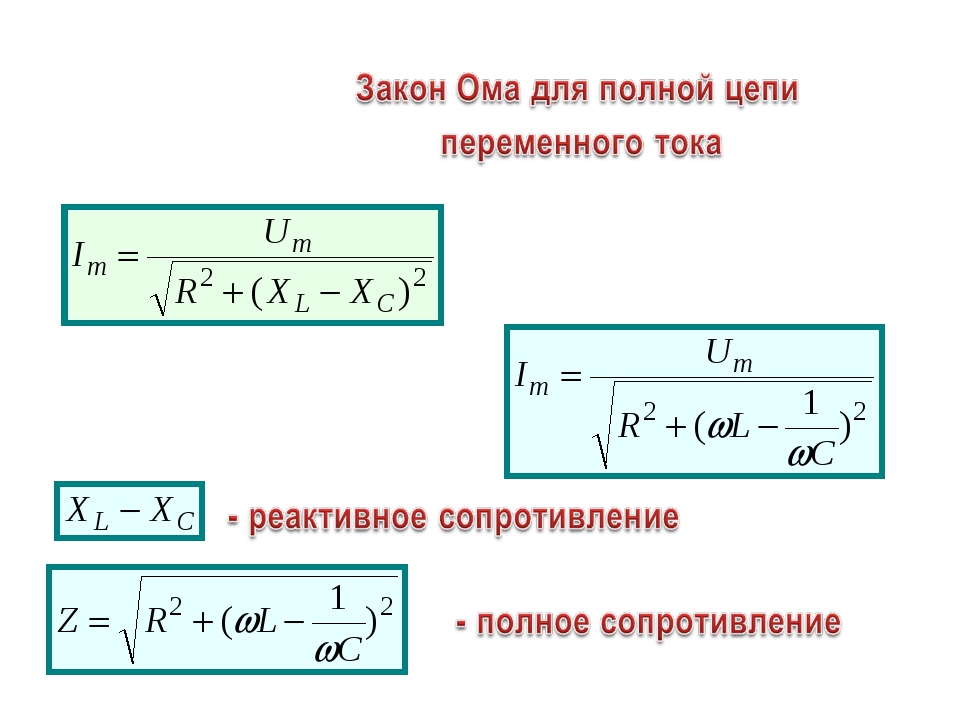
довольно легко работают в цепи постоянного тока; они сопротивляются току, протекающему через какой-то металл, например медь.Вы добавляете резистор 220 кОм в цепь постоянного тока, и вы получаете определенное уменьшение тока между одной стороной резистора и другой. Резисторы, как и другие нереактивные компоненты, меньше заботятся о таких вещах, как частота источника питания. Они просто будут продолжать делать то, что делают, все время сопротивляясь одной и той же силе тока.
Но что будет, если вы начнете работать с электроникой с питанием от переменного тока? С переменным током это не просто вопрос питания вашей цепи напряжением 5 В.Вместо этого у вас есть новые переменные, которые нужно учитывать, например, конкретную частоту вашего переменного тока. Здесь, в Соединенных Штатах, переменный ток движется вперед и назад со скоростью 60 циклов в секунду (60 Гц). Над прудом, в Европе, частота 50 Гц.
В отличие от прямого постоянного тока, переменный ток колеблется вперед и назад с заданным количеством циклов в секунду. (Источник изображения)
(Источник изображения)
Суть всего в том, что в электронике с питанием от переменного тока вам нужны не только нереактивные компоненты, такие как резисторы для сопротивления току.Вам также понадобятся компоненты, которые могут реагировать на на изменения тока и частоты, такие как конденсаторы и катушки индуктивности; в противном случае ваша схема не будет работать должным образом. Сложите все это вместе, и вы почти сможете думать об импедансе как о старшем брате сопротивления. Импеданс включает в себя как сопротивление, так и реактивное сопротивление. Или выражается как отношение:
Импеданс = Сопротивление + Реактивное сопротивление
Но что такое реактивность?
Reactance бывает двух разных видов в зависимости от того, какой реактивный компонент вы используете, к ним относятся:
Индуктивное реактивное сопротивление
Вы увидите это в виде электромагнитов, которые изменяют магнитное поле в цепи, также называемой индуктором. Катушки индуктивности будут иметь низкий импеданс на низких частотах и высокий импеданс на высоких частотах.
Катушки индуктивности будут иметь низкий импеданс на низких частотах и высокий импеданс на высоких частотах.
Связка индукторов, обратите внимание на общность, катушка с медным проводом вокруг магнита. (Источник изображения)
Емкостное реактивное сопротивление
Вы увидите это в виде заряжающего электрического поля между двумя проводящими поверхностями, также называемого проводником. Проводники имеют высокий импеданс на низких частотах и низкий импеданс на высоких частотах.
Конденсаторы бывают разных форм и размеров.(Источник изображения)
Поместите резисторы, катушки индуктивности и конденсаторы в цепь переменного тока, и вы не только сможете противостоять электричеству, но также сможете накапливать и выделять энергию. В то время как резистор будет поддерживать постоянное сопротивление независимо от меняющихся условий, катушки индуктивности и конденсаторы изменят свое сопротивление в зависимости от частоты сигнала, который они представляют. А когда конденсаторы и катушки индуктивности сопротивляются и накапливанию / высвобождению энергии, тогда у вас есть мера импеданса.
А когда конденсаторы и катушки индуктивности сопротивляются и накапливанию / высвобождению энергии, тогда у вас есть мера импеданса.
Как измерить импеданс?
Давайте возьмем простую схему, чтобы связать все это вместе. Взгляните на первый ниже; это цепь с питанием от постоянного тока с током, протекающим через резистор. Довольно просто, правда? Чем выше сопротивление в этой цепи, тем меньше будет ток.
Простая цепь постоянного тока с резистором 100 Ом для ограничения тока.
Но что произойдет, если вы модернизируете эту схему с помощью источника переменного тока, катушки индуктивности и конденсатора? Теперь у вас есть два дополнительных компонента, обеспечивающих собственное сопротивление электрическому току.Как и резистор, они оба препятствуют потоку тока , а также реагируют на него. Когда вы объединяете сопротивление своего резистора, сопротивление и реактивное сопротивление конденсатора и катушки индуктивности вместе, вы получаете полное сопротивление.
Последовательная цепь переменного тока с резистором, катушкой индуктивности и конденсатором.
Но подождите, вычислить импеданс не так просто, как сложить сопротивление и реактивное сопротивление, и именно здесь большинство руководств начинается с набора математических формул.Так что давайте продолжим эту часть медленно.
Расчет импеданса конденсатора
Чтобы рассчитать импеданс нашего конденсатора, вы можете использовать приведенную ниже формулу. Здесь X C — это полное сопротивление, которое вы получите, которое измеряется в Ом (Ом). f — это частота сигнала, проходящего через конденсатор, а C — это емкость.
Расчет импеданса индуктора
Чтобы рассчитать импеданс нашей катушки индуктивности, вы можете использовать приведенную ниже формулу.Здесь X L — это полное сопротивление, которое вы получите, которое снова измеряется в Ом (Ом). f — это частота сигнала, проходящего через вашу катушку индуктивности, а L — это индуктивность.
f — это частота сигнала, проходящего через вашу катушку индуктивности, а L — это индуктивность.
Эти формулы хороши и хороши, если вам просто нужны измерения импеданса для отдельных компонентов, но что, если вы хотите знать полное сопротивление для всей вашей цепи? Здесь все становится сложнее.
Прежде чем мы перейдем к нашей последней формуле, мы хотим предложить вам калькулятор импеданса, который может облегчить вашу жизнь: Калькуляторы импеданса от Кейсана.
Расчет общего импеданса
Для выполнения работы вам понадобится помощь теоремы Пифагора. Как мы объясняли выше, в цепях переменного тока вы будете работать как с сопротивлением, так и с реактивным сопротивлением, которые вместе дают вам общее сопротивление. Но дело не просто в сложении сопротивления и реактивного сопротивления. Мы могли бы объяснить почему, но это позволило бы погрузиться в тонкости векторов и фазоров, а это уже целый блог.
Когда вы разбиваете процесс вычисления импеданса для всей цепи, вы получите так называемый треугольник импеданса, посмотрите это ниже:
Треугольник импеданса позволяет легко рассчитать импеданс для всей вашей цепи.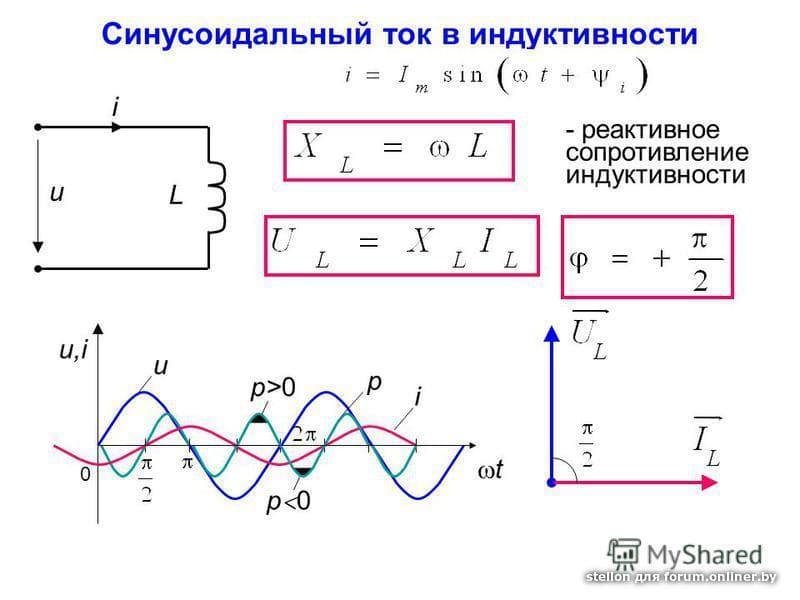 (Источник изображения)
(Источник изображения)
Самая важная часть этого треугольника — гипотенуза, которая дает вам полное сопротивление, основанное на квадратном корне из вашего реактивного сопротивления и сопротивления. Если вы поместите это в формулу, вы можете найти свой общий импеданс по формуле, приведенной ниже. Здесь Z — ваше полное сопротивление, R — ваше полное сопротивление, а X — ваше полное реактивное сопротивление.
Практический импеданс
Видите ли, понять электрический импеданс не так уж и сложно, в конце концов, не так ли? Есть масса бесплатных калькуляторов, которые помогут вам в работе.Что вам действительно нужно знать, так это то, что импеданс работает так же, как сопротивление, препятствуя протеканию тока в цепи с питанием от переменного тока.
Именно способность компонентов, таких как конденсаторы и катушки индуктивности, реагировать на постоянно меняющийся переменный ток, делает их уникальными. Из-за сопротивления у вас может быть что-то вроде блока предохранителей в вашем доме, который будет реагировать на неожиданный скачок напряжения, предотвращая перегорание электрической системы вашего дома. И вы также можете поблагодарить импеданс за возможность носить с собой портативный ноутбук, зная, что ваши батареи полностью заряжены и не взорвутся.
Из-за сопротивления у вас может быть что-то вроде блока предохранителей в вашем доме, который будет реагировать на неожиданный скачок напряжения, предотвращая перегорание электрической системы вашего дома. И вы также можете поблагодарить импеданс за возможность носить с собой портативный ноутбук, зная, что ваши батареи полностью заряжены и не взорвутся.
Когда дело доходит до работы с устройствами с питанием от переменного тока, будь то ноутбук или блок предохранителей в вашем доме, вам нужно поблагодарить за сопротивление. И помните, что электрическое сопротивление — это просто старший брат сопротивления, объединяющий сопротивление и реактивное сопротивление в одной простой формуле.
Готовы приступить к разработке своей первой электроники с питанием от переменного тока? Попробуйте Autodesk EAGLE бесплатно сегодня!
Импеданс в цепях RLC — Инструментальные средства
Импеданс в последовательной цепи R-C-L равен векторной сумме сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления (рисунок 8).
Рисунок 8: Анализатор импеданса серии R-C-L
Приведенные ниже уравнения представляют собой математические представления импеданса в цепи R-C-L. Поскольку разница между X L и X C возведена в квадрат, порядок, в котором вычитаются количества, не влияет на ответ.
Пример:
Найдите полное сопротивление последовательной цепи R-C-L, когда R = 6 Ом, X L = 20 Ом и X C = 10 Ом (рисунок 9).
Рисунок 9: Простая цепь R-C-L
Решение:
Z = √ {R 2 + ( X L — X C ) 2 }
Z = √ {6 2 + (20 — 10) 2 }
Z = √136
Z = 11,66 Ом
Импеданс в параллельной цепи R-C-L равен напряжению, деленному на общий ток.
Уравнение ниже представляет собой математическое представление импеданса в параллельной цепи R-C-L.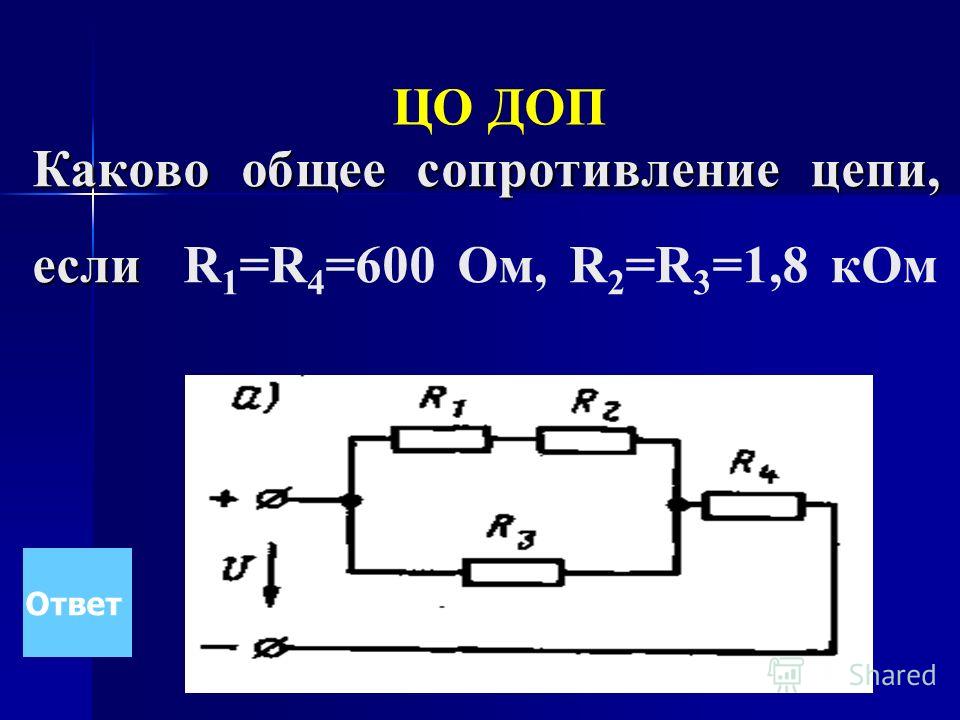
, где
Z T = полное сопротивление (Ом)
В T = общее напряжение (В)
I T = общий ток (A)
Полный ток в параллельной цепи R-C-L равен квадратному корню из суммы квадратов тока, протекающего через ветви сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления цепи.
Приведенные ниже уравнения представляют собой математические представления полного тока в параллельной цепи R-C-L.Поскольку разница между I L и I C возведена в квадрат, порядок, в котором вычитаются количества, не влияет на ответ.
, где I C > I L , применяется первое уравнение, а когда I L > I C применяется второе уравнение.
где
I T = полный ток (A)
I R = ток через резистивную ветвь цепи (A)
I C = ток через емкостную реактивную ветвь цепи (A)
I L = ток через ветвь индуктивного сопротивления цепи (A)
Пример:
Резистор 200 Ом, резистор 100 Ом X L и 80 Ом X C подключаются параллельно к источнику переменного тока 120 В (рисунок 10). Найдите: (1) токи ответвления, (2) полный ток и (3) полное сопротивление.
Найдите: (1) токи ответвления, (2) полный ток и (3) полное сопротивление.
Рисунок 10: Простая параллельная цепь R-C-L
Решение:
1. Токи ответвления
I R = V T / R = 120/200 = 0,6 A
I L = V T / X L = 120/100 = 1,2 A
I C = V T / X C = 120/80 = 1,5 A
2. Итого текущий
I T = √ {I R 2 + (I C — I L ) 2 }
I T = √ {0.6 2 + (1,5 — 1,2) 2 }
I T = √ {0,36 + 0,09}
I T = √0,45 = 0,671 A
3. Импеданс
Z = V T / I T
Z = 120 / 0,671
Z = 178,8 Ом
Эквивалентный импеданс— обзор
Импеданс верхней индуктивной ветви равен
Z 1 = (8 + j10) ω = √ (8 2 + 10 2 ) ∠ tan −1 (10/8) ω
, поэтому
Z 1 = 12. 81∠51,34 ° ω
81∠51,34 ° ω
Импеданс нижней индуктивной ветви равен
Z 2 = (7 + j9) ω = √ (7 2 + 9 2 ) ∠ tan −1 ( 9/7) ω
, поэтому
Z 2 = 11,4∠52,13 ° ω
Сейчас
Z 1 + Z 2 = (8 + 7) + j (10 + 9) = (15 + j19) ω = √ (15 2 + 19 2 ) ∠ tan −1 (19/15) ω
, поэтому
Z 1 + Z 2 = 24.2∠51,7 ° ω
Эквивалентное сопротивление параллельных индуктивных ветвей составляет
Z1Z2 / (Z1 + Z2) = [(12,81 × 11,4) / 24,2] ∠ (51,34 + 52,13-51,7) = 6,03∠51,77 ° ω = 6,03 (Cos51,77 + j sin51,77) = (3,73 + j4,73) ω
Импеданс емкостной ветви
Z 3 = (5 — j2) ω
Полное сопротивление полный контур,
Z eq = Z 3 + Z 1 Z 2 / ( Z 1 + Z 2 ) = (5 + 3.

 Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.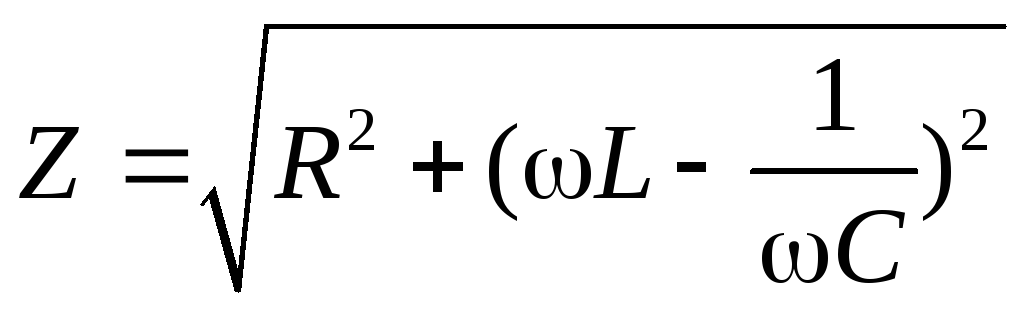 {j \ omega t} + {\ text {Const}} = {1 \ over j \ omega C} i_ {C} (t) + {\ text {Const}}.}
{j \ omega t} + {\ text {Const}} = {1 \ over j \ omega C} i_ {C} (t) + {\ text {Const}}.} {2} LC = 1.}
{2} LC = 1.} Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
 Проверка демпфера для включения параллельно осветительной арматуре.
Проверка демпфера для включения параллельно осветительной арматуре.