Updating… ! 1 _1 работа и мощность электрического тока.swf(200k) Ольга Федотова, 5 янв. 2016 г., 10:11 (15k) Ольга Федотова, 5 янв. 2016 г., 10:11 1_2 формула работы электрического тока.swf(15k) Ольга Федотова, 5 янв. 2016 г., 10:11 2 работа электрического тока.swf(122k) Ольга Федотова, 5 янв. 2016 г., 10:11 3 задача мощность.swf(45k) Ольга Федотова, 5 янв. 2016 г., 10:11 3 задачи.swf(120k) Ольга Федотова, 5 янв. 2016 г., 10:11 3 мощность тока таблица.jpg(56k) Ольга Федотова, 5 янв. 2016 г., 10:11 ć 3 решение задач moschnost_toka. ppt(368k) Ольга Федотова, 5 янв. 2016 г., 10:11 (28k) Ольга Федотова, 5 янв. 2016 г., 10:11 ć 4 Тест к уроку Работа и мощность электрического тока.ppt(101k) Ольга Федотова, 5 янв. 2016 г., 10:11 ć 4 мощность электрического тока.ppt(179k) Ольга Федотова, 5 янв. 2016 г., 10:11 ć 4 работа электрического тока.pptx(234k) Ольга Федотова, 5 янв. 2016 г., 10:11 ĉ 4 самостоятельная работа.doc(35k) Ольга Федотова, 5 янв. 2016 г., 10:11 |
Счетчики электроэнергии, которые стоят в квартирах, как бы сочетают в себе все эти вышеперечисленные приборы в одном. Они измеряют работу, совершенную током. Работа тока в нашей квартире – это энергия, которую он израсходовал на всех включенных в сеть квартиры приборах. Это и есть то, за что мы платим. Однако, мы платим не за джоули, а за киловатт-часы.
Просто величина мощности в 1 ватт – это очень небольшая мощность, и если бы мы платили за ватты-в-секунду, мы бы оплачивали десятки и сотни тысяч таких единиц. Для упрощения расчетов и приняли единицу «киловатт-час».Интерактивный тест и мощность
электрического тока…мощность постоянного тока
Немного о мощности постоянного тока. Не надо долго ходить за примерами и что-то объяснять в том плане, что механическая работа, которую совершает двигатель, выделяемая нагревателем теплота вполне измеримы. От каких же величин зависит совершаемая работа?
И тем больше количество произведенной работы. Но и при простом увеличении количества потребителей сила тока увеличивается, поскольку обычно они включаются параллельно. Следовательно, произведенная электрическая работа возрастает с увеличением силы тока и времени. Но влияет еще и третья величина. Две параллельно включенные лампы потребляют двойную энергию по сравнению с одной. А, значит, и двойной ток. Тот же результат получим, если соединим две лампы последовательно и подадим двойное напряжение (см. рис.1).W=UIt
Здесь U — напряжение, I — сила тока, t — время, W — количество произведенной работы. Теперь о самой мощности. Под мощностью понимают работу, совершаемую за определенное время. Таким образом, P=W/t. Если теперь вместо W подставить выражение для электрической работы, то
P=UIt/t=UI
Таким образом, мощность — это произведение напряжения на силу тока.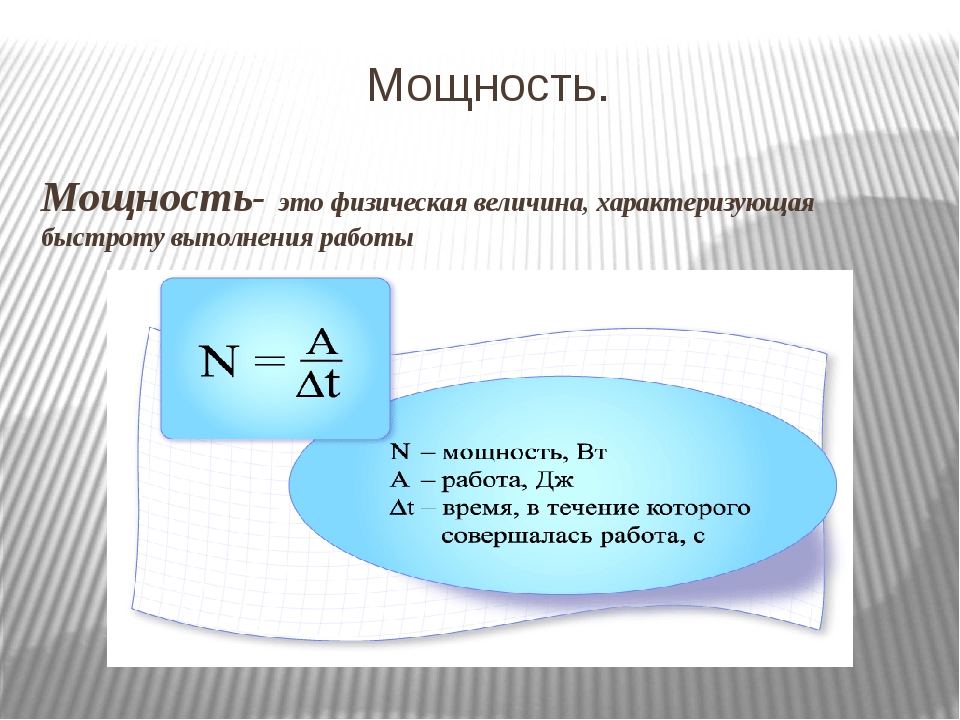
Вернувшись назад к формуле работы тока W=UIt увидим, что это произведение электрической мощности P=UI и времени t, в течение которого эта мощность действует. Если время выразить в часах, то плучим количество потребленной энергии «ватт-час». Такая единица измерения является маленькой, поэтому пользуются «киловатт-часом». 1кВтч=1000Втч
Кстати, кто еще далек от электричества, есть «хитрый» перерасчет электрической мощности в механическую:
1кВтч=367000кгс*м; 1кВт=102кгс*м/с
Constant-Current — Электрический ток в физике
Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту.
Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи.
Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,
где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.
Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим
Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:
Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле
По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.
Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа Ameh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия.
Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:
Затраченная же работа источника тока равна работе сторонних сил:
где .
Тогда .
КПД источника , где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f(R) при r = const приведена на рис. 1.
Рис. 1
Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж. 1 Дж = Кл·В = А·В·с.
Измеряют работу электрического тока счетчиками.
Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле или P = IU.
Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока: .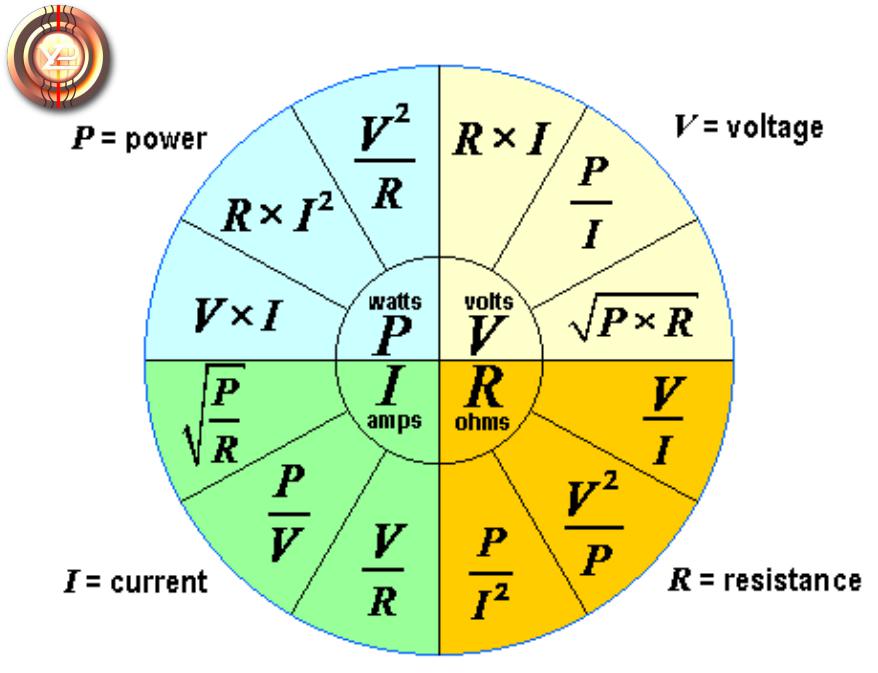
В этом случае речь идет о тепловой мощности.
Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.
Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·106 Дж = 3,6 МДж; 1 гВт·ч = 3,6·105 Дж = 360 кДж.
Для измерения мощности тока существуют специальные приборы — ваттметры.
Формула мощности в физических уравнениях и примерах | Что такое уравнение мощности? — Видео и стенограмма урока
Примеры силы в физике
Для более глубокого понимания силы полезно увидеть несколько примеров силы в физике. Мощность может быть рассчитана несколькими способами и может использоваться для расчета других величин, например скорости. Ниже приведены несколько примеров.
Пример 1: Использование формулы мощности в физике
Вот пример того, как использовать формулу мощности.Рассмотрим приведенный выше пример, где человек применяет силу, чтобы переместить ящик. Человек прикладывает силу 7 Н и перемещает ящик на 3 м.
На это у человека уходит 9 секунд. В чем сила человека?
Первым делом нужно рассчитать работу. Это можно вычислить согласно
{eq} W = Fd {/ eq}
Подстановка известных значений дает
{eq} W = (7N) (3m) {/ eq}
Итак, работа { eq} W = 21 Дж {/ экв}. Следующим шагом является расчет мощности в соответствии с уравнением рабочего времени для мощности, которое составляет
{eq} P = W / t {/ eq}
Следовательно, мощность составляет
{eq} P = 21J / 9s {/ eq}
Сила человека равна {eq} 2.3 Вт {/ экв}.
Пример 2: Как найти силу в физике
Рассмотрим другой пример. Лифт может доставить на второй этаж здания человека и несколько ящиков общей массой 500 кг. Если лифт имеет номинальную мощность 1500 Вт, как быстро он может перемещать человека и ящики?
Первый шаг — вычислить силу, необходимую для перемещения человека и ящиков вверх.
2) {/ eq}
Итак, необходимое усилие составляет {eq} 4900N {/ eq}. Следующим шагом является использование уравнения сила-скорость, которое составляет
{eq} P = Fv {/ eq}
. Преобразование этого уравнения для нахождения скорости дает
{eq} v = P / F {/ eq}
.Следовательно, скорость равна
{eq} v = (1500 Вт) / (4900N) {/ eq}
{eq} v = 0,3 м / с {/ eq}
Пример 3: Расчет мощности в физике
Вот еще один пример того, как найти силу в физике. Скалолаз массой 65 кг поднимается прямо по склону горы.Они преодолевают расстояние 15 м за 35 секунд. При той же выходной мощности, с какой скоростью они могли подниматься с рюкзаком массой 12 кг?
Первым шагом к решению этой проблемы является расчет выходной мощности скалолаза. Для этого необходимо рассчитать силу, используя
{eq} F = mg {/ eq}
Итак, сила составляет
{eq} F = (65 кг) (9.
2) = 637N {/ eq}
Следующий шаг — вычислить работу по формуле
{eq} W = Fd {/ eq}
Следовательно, работа будет равна
{eq} W = (637N) (15 м) = 9555 Дж {/ экв}.
Теперь можно рассчитать выходную мощность
{eq} P = W / t {/ eq}
Таким образом, выходная мощность альпиниста равна {eq} P = (9555 Дж) / (35 с) = 273 Вт. {/ eq}
Теперь, предполагая ту же выходную мощность, скорость можно рассчитать, используя
{eq} v = P / F = P / mg {/ eq}
Масса скалолаза и рюкзака равна 77 кг, замена известных значений дает
{eq} v = (273W) / (77kg \ times9.2) = 0,4 м / с {/ eq}
Таким образом, скалолаз может подняться со скоростью {eq} 0,4 м / с {/ eq} с рюкзаком.
Сводка урока
Power описывает, как быстро энергия используется или передается. Его также можно рассматривать как работу, выполненную за единицу времени. В результате единица мощности — джоули в секунду, также известная как Вт .
Концепция мощности может применяться во многих повседневных ситуациях, таких как вождение автомобиля, подъем по лестнице и перемещение мебели.
Мощность можно рассчитать одним из двух способов. Уравнение рабочего времени включает деление работы на время. Уравнение сила-скорость умножает силу на скорость, пока скорость постоянна. Эти уравнения можно использовать для решения проблем, связанных с мощностью. Примеры, представленные в этом уроке, показывают, как можно рассчитать мощность в таких ситуациях, как перемещение тяжелых предметов по горизонтали и вертикали. Они также показали, как мощность связана с работой, силой и скоростью.
Формула мощности— Javatpoint
Мощность определяется как количество работы, выполненной за единицу времени . Мощность требуется везде для выполнения задачи, будь то физическая или механическая. Концепция остается прежней, то есть способность, необходимая для выполнения задачи в определенное время.
Характеристики мощности
Характеристики мощности следующие:
- Один ватт определяется как 1 джоуль энергии в секунду.
- Это скалярная величина.
- Власть часто определяют как деятельность.
- Мощность — это производная от проделанной работы по времени. Его можно выразить как P = dW / dt.
- Мощность также измеряется в лошадиных силах, что равняется 745,7 Вт.
- Другие единицы мощности: киловатт, милливатт, эрг в секунду, дБм (децибел-милливатт) и калория в час .
- Объем работы, выполненной за раз, может быть разным для разных веществ. Например, TNT (тринитротолуол) обеспечивает большую мощность по сравнению с углем.Это потому, что реакция TNT высвобождает энергию быстрее, чем уголь.
- В механической системе входная мощность может быть равна выходной мощности, если в системе нет таких потерь.
Мы можем определить формулу мощности как механическую мощность, гравитационную силу, электрическую мощность и мощность в терминах силы, смещения и скорости .
Он приведен ниже:
Давайте обсудим различные формулы мощности.
Механическая мощность
Определяется как энергия системы в единицу времени.
P = E / t
Где,
П — мощность
E — энергия
T — время
Ватт, джоуль и секунда — это единицы мощности, энергии и времени.
Мощность также выражается как:
P = w / t
Где,
Вт — проделанная работа, t — время, P — мощность.
Сила тяжести
Измеряется относительно g, гравитационной постоянной, равной 9.8 метров на вторую площадь. Сила гравитации выражается как:
P = мг / т
Где,
П — мощность
м масса
h — высота
т — время
Масса обычно измеряется в килограммах, а высота — в метрах.
Электроэнергетика
Электрическая мощность выражается как:
P = V I
Где,
П — мощность
В — напряжение
I — текущий
Электрическая мощность определяется как произведение тока и потенциала в цепи.
2R
Мощность, выраженная в силе, перемещении и скорости
Выражается как:
Мощность = Сила x Смещение / Время
P = Fs / t
Где,
F — сила, измеренная в Ньютонах
S — смещение, измеренное в метрах
T — время
Мы также можем записать приведенное выше уравнение как:
P = Сила x скорость
P = Fv
(Как скорость = смещение / время)
Давайте обсудим числовые примеры и MCQ по мощности для лучшего понимания.
Числовые примеры
Рассмотрим следующие примеры.
Пример 1: Электрическая машина использует энергию 200 Дж за 10 секунд. Найдите мощность, которую использует машина?
Решение: Указанные параметры:
E = 200 Дж
T = 10 с
Мощность определяется по:
P = E / т
P = 200/10 = 20 Вт
Таким образом, мощность, необходимая для машины, составляет 20 Вт.
Пример 2: Генри имеет массу 50 кг и поднимается на высоту 10 м за 20 секунд.Найдите силу.
Решение: Приведены следующие параметры:
Масса = 50 кг
Высота = 10 м
Время = 20 секунд
Сила тяжести может быть вычислена как P = mgh / t
Где, g = 9,8 метра в секунду в квадрате
P = 50 x 9,8 x 10/20
P = 245 Вт
Таким образом, мощность 245 Вт.
Пример 3: Напряжение и ток электрической цепи указаны как 15 В и 2 А.Найдите электрическую мощность цепи.
Решение: Приведены следующие параметры:
Напряжение = 15 Вольт
Ток = 2 Ампера
P = V x I
P = 15 x 2 = 30 Вт
Таким образом, мощность электрической схемы 30 Вт.
Пример 4: К объекту, движущемуся с постоянной скоростью 4 м / с, прилагается постоянная сила 10 Н. Вычислите мощность.
Решение: Приведены следующие параметры:
Сила = 10 Н
Скорость = 4 м / с
Мощность может быть вычислена как, P = Сила x скорость
P = 10 x 4 = 40 Вт
Таким образом, мощность 40 Вт.2R
P = 3 x 3 x 2
P = 18 Вт
Таким образом, мощность 8 Вт.
Вопросы с несколькими вариантами ответа по питанию
MCQ, основанные на формуле мощности, следующие:
1) Что из следующего является правильной формулой мощности?
- Мощность = проделанная работа x время
- Мощность = энергия / время
- Мощность = сила x время
- Мощность = скорость / время
Ответ: (б) Мощность = энергия / время
Описание: Правильная формула мощности из вышеприведенного варианта: P = E / t.
2) S.I. единица мощности:
- Джоулей
- Ньютон
- Ампер
- Вт
Ответ: (d) Ватт
Описание: Согласно Международной системе единиц, единицей мощности является ватт.
3) Название устройства, используемого для измерения мощности:
- Вольтметр
- Амперметр
- Ваттметр
- Ничего из вышеперечисленного
Ответ: (в) Ваттметр
Описание: Ваттметр обычно используется для измерения электрической мощности в цепи.
4) Киловатт-час — это единица измерения?
- Скорость
- Сила
- Энергия
- Мощность
Ответ: (c) Энергия
Описание: Мощность = энергия / время
Итак, энергия = мощность x время
Энергия = киловатт x час = киловатт-час
Здесь киловатт и час — единица мощности и времени.
5) Мощность прямо пропорциональна:
- Напряжение
- Текущий
- Оба (а) и (б)
- Ничего из этого
Ответ: (в) И (а), и (б)
Описание: Формула мощности — I ^ 2R или V ^ 2 / R.Это означает, что мощность прямо пропорциональна как напряжению, так и току.
Перекрестная проверка трех уравнений мощности скачка
Оценка вертикального прыжка и досягаемости используется в качестве компонента при оценке пиковой механической мощности в двух уравнениях, предложенных Льюисом и Харманом и др.
Цель: Целью настоящего исследования было: 1) перекрестная проверка двух уравнений с помощью теста вертикального прыжка и досягаемости, 2) разработка более точного уравнения для большой неоднородной популяции, 3) анализ гендерных различий и протоколов прыжков, и 4) оценить прогнозируемую остаточную сумму квадратов (PRESS) в качестве процедуры перекрестной проверки.
Методы: Сто восемь спортсменов мужского и женского пола, а также не спортсменов были протестированы на силовой платформе. Они выполнили по три вертикальных прыжка с максимальным усилием, каждый из которых является приседом (SJ) и прыжком с обратным движением (CMJ), одновременно выполняя тест вертикального прыжка и досягаемости. Регрессионный анализ использовался для прогнозирования пиковой мощности на основе массы тела и высоты вертикального прыжка.
Полученные результаты: Данные SJ дали лучшее уравнение для прогнозирования мощности, чем данные CMJ, из-за большей изменчивости метода CMJ. Следующее уравнение было получено из данных SJ: Пиковая мощность (Вт) = 60,7x (высота прыжка см]) + 45,3x (масса тела [кг]) — 2055. Это уравнение показало большую точность, чем у Льюиса или предыдущего Harman et al. уравнения и заниженная пиковая мощность менее чем на 1% с SEE 355.0 Вт с использованием протокола SJ. Использование одного уравнения для мужчин и женщин привело лишь к незначительной (5% выходной мощности) разнице между полами. Использование данных CMJ в уравнении, выведенном из SJ, привело к завышению пиковой мощности только на 2,7%. Перекрестная проверка уравнений регрессии с помощью PRESS выявляет точные и надежные значения R2 и SEE.
Выводы: Уравнение SJ является немного более точным уравнением, чем уравнение, полученное на основе данных CMJ.Это уравнение следует использовать при определении пиковой мощности вместо формул, разработанных как Harman et al. и Льюис. Отдельные уравнения для мужчин и женщин не нужны.
Формулы для расчета коэффициента мощности— RF Cafe
Коэффициент мощности измеряет фазовый угол между мгновенным напряжением и мгновенным током в цепи. Напряжение ( E ) опережает ток ( I ) на 90 ° по индуктивной ( L ) цепи и напряжение ( E ) отстает от тока ( I ) на 90 ° в емкостной ( C ) цепи.
Популярный мнемоник — ELI ICE человек, так как E ведет (идет впереди) I в ELI, а E отстает (идет после) I в ICE.
| коэффициент мощности (P f ) = cos (q) | |
| Полная мощность (P) = I * В | |
| Истинная мощность = P | |
| I = ток | |
| q = фазовый угол | |
| В = Напряжение |
| Формулы мощности | ||||
| Полная мощность P = I * V P = I 2 * R P = V 2 / R | Истинная мощность P = I * V * cos (q) P = I 2 * Z * cos (q) P = V 2 * cos (q) / Z P = P a * P f | Импеданс Z = V 2 * cos (q) / P Z = P / [I 2 * cos (q)] | ||
| Ток I = P / [V * cos (q)] I = sqrt {P / [Z * cos (q)]} | Напряжение В = P / [I * cos (q)] В = sqrt [P * Z / cos (q)] | |||
| ||||
Формулы расчета оптической силы ИОЛ Оптимизация по Haigis Holladay SRKT Hoffer Q
Для осевой длины от 22.От 50 мм до 24,00 мм, центральной оптической силы роговицы от 42,00 D до 45,00 D и нормальной глубины передней камеры, большинство современных формул расчета оптической силы ИОЛ дадут хорошие результаты. Однако для глаз за пределами этого диапазона наши результаты показывают, что Haigis (с правильно оптимизированными константами a0, a1 и a2) и формулы нового поколения, такие как Holladay 2, Olsen и Barrett, дают лучшие результаты.
Для Holladay 1, SRK / T, Haigis и Holladay 2 требуется регулировка для большой и крайней осевой миопы и осевой длины более 25.00 мм. Как это сделать, описано по адресу:
.http://www.doctor-hill.com/iol-main/extreme_axial_myopia.htm
Документ The Journal of Cataract and Refractive Surgery, в котором описывается этот подход, можно найти по адресу:
Wang L, et al. Оптимизация расчета оптической силы интраокулярных линз в глазах с осевой длиной более 25,0 мм. JCRS 2011; 37: 2018-2027.
Здесь есть над чем подумать. Как хирургов, нас сейчас в основном оценивают наши пациенты и коллеги по нашим рефракционным результатам.Кажется немного странным тратить десятки тысяч долларов на следующую по точности измерительную технологию, но по-прежнему полагаться на методы расчета, которые не из этого века. Для получения оптимальных результатов требуются наилучшие измерительные технологии и наилучшие методы расчета.
В приведенной ниже таблице представлен наш опыт использования популярных методов выбора мощности ИОЛ, когда измерения проводились с помощью оптической биометрии.Сейчас мы используем только формулу Barrett Universal II и метод распознавания образов Hill-RBF для всех наших расчетов. Для сильной и крайней осевой миопы мы также рассмотрим модификацию осевой длины Ванга-Коха формулы Holladay 1. Восемь лет опыта показали, что лучшие предоперационные измерения были с Haag-Streit Lenstar.
СерияPower / Великая формула Эйлера | Деривативы (12 видео) | Основные моменты Calculus
Связанные ресурсы
Краткое содержание лекции и практические задачи (PDF)
ГИЛБЕРТ СТРАНГ: Хорошо, я думал, что сегодня расскажу о степенных рядах.Это степени x. Я буду продолжать. Все силы, от x до четвертого, от x до пятого, тоже войдут. И моя идея состоит в том, чтобы объединить их, сложить, чтобы получить функцию от x. Итак, мы занимаемся расчетом, но это новая его часть, с этими бесконечными рядами.
Итак, что я подразумеваю под их объединением? Я имею в виду, что я умножу эти силы на некоторые числа. Позвольте мне позвонить по этим номерам a0. Итак, этот первый парень будет a0, а затем я добавлю a1 x. Я кончил. Я добавлю a2 x в квадрате, a3 x в кубе и далее.Итак, теперь у меня есть функция. И эту функцию позвольте мне назвать f of x. Итак, вот мой начальный план.
Ну, мы видели это от е до х. Позвольте мне вспомнить, как может появиться e к x, ряду для этой конкретной функции. Итак, вот план. Я собираюсь выбрать эти а так, чтобы они совпадали — позвольте мне записать эти слова. Я сопоставлю, когда x равно 0. Функция, ее производная, ее следующая производная, ее третья производная и далее.
Каждый a, как и a3, будет выбран таким образом, чтобы в правой части была правильная производная, третья производная, при x, равном 0.Итак, этот ряд Тейлора — имя Тейлора связано с подобным рядом — все происходит в точке x, равной 0.
Итак, в случае от е до x, все его производные были одинаковыми. Еще е до х. И все они равны 1 при x равном 0. Поэтому я хочу, чтобы эта функция давала мне 1 для каждой производной. Это не значит, что все а должны быть 1.
Почему бы и нет? Потому что, когда я возьму производную, например, этого парня, эта первая производная в кубе x будет равна 3x в квадрате. Следующая производная 6х.Следующая производная 6. Это то, что я хочу. Это третья производная, но это будет 6, поэтому a3 должно быть 1/6, чтобы дать мне правильный ответ 1. Позвольте мне записать эти вещи.
Итак, мы только что сделали производную от x до n-го. N-я производная. Какая n-я производная от x до n? Мы можем использовать нашу красивую формулу для производных. Итак, первая производная равна nx до n минус 1. Производная от этой производной будет n умножить на n минус 1 x в одну меньшую степень. Продолжайте, сделайте это n раз, и что у вас есть?
Наконец-то вы перешли к 0-й степени x, постоянной.Но что это за константа? Это n умноженное на n минус 1, так что n-я производная будет равна n от первой, n минус 1 от второй. Продолжайте умножать, пока, наконец, не дойдете до 1. И, конечно же, он называется потому, что встречается достаточно часто, чтобы иметь собственное особое имя. Это имя n факториал. И написано с восклицательным знаком. Итак, это n факториал и n-я производная x от n.
Итак, для конкретной функции e от x, если я вычислил ее ряд, все производные, которые я пытаюсь получить, будут равны единице.Но что силы x дают мне эти n факториалов. Лучше делить a на факториал n. Итак, позвольте мне вспомнить серию от e до x, а затем перейти к новым функциям. В этом суть моей лекции. Итак, мы переводим e в x немного иначе, чем в оригинале, но это хороший способ. От е до x в точке x, равной 0, будет 1. При первой производной от e до x равна 1, поэтому я делю на 1 факториал. Это 1. Но здесь мне нужно разделить на 2, потому что вторая производная равна 2, и я хочу, чтобы их отменили.И здесь я делю на … на что делить? 6, потому что третья производная равна 6. И типичный член — мне нужно разделить на n факториал, потому что, когда я беру n производных, я получаю n факториал. N-я производная от того, что мы только что разработали, является n-факториальной. Итак, я делю факториал на n, и у меня получается производная 1. И это правильно, если e до x. Итак, план состоит в том, чтобы сопоставление производных в x равнялось 0 каждой степенью x. И теперь я готов к новой функции. И хороший выбор — sine x.
Итак, теперь на этой доске, если я могу прийти сюда, я возьму на себя другую функцию. Больше не е на х. Моя функция будет синусом x. Что ж, я лучше разберусь со всеми его производными. И они, конечно, милые. Синус x, его производная. Могу я просто перечислить их все? Это то, чему я должен соответствовать. Я подставлю x равным 0. Но позвольте мне сначала найти производные. Производная синуса — косинус. Производная косинуса минус синус. Производная минус синуса минус косинус.А потом я снова возвращаюсь к синусу и повторяю до бесконечности. Это список производных синуса x. Это мой f of x здесь. Этот парень, первый.
Хорошо, теперь я подключаю x, равный 0, потому что я хочу, чтобы все производные были равны 0. Вся серия строится с фокусом на этой точке, x равно 0. Таким образом, при x, равном 0, это легко подключить. Синус равен 0 , косинус равен 1, минус синус равен 0. Минус косинус равен минус 1. Синус равен 0. И повторите. 0, 1, 0, минус 1 навсегда.
Хорошо, я знаю производные, которые мне нужно сопоставить.Теперь могу я построить соответствующий этому степенной ряд?
Хорошо, так что степенной ряд даст мне синус x, а что он будет иметь? Он начинается с 0. Постоянный член равен 0, потому что синус 0, когда x равен 0 — конечно, мы хотим получить ответ 0.
Затем следующий член, x, его коэффициент равен 1. 1x . Нет x в квадрате синуса x. Нет x в квадрате. Но теперь минус. У меня есть минус 1x в кубе? Не совсем. Минус x в кубе, но мне нужно разделить на 6, потому что когда я возьму эти три производные, получится 6.Поэтому мне нужно разделить на 6, что составляет 3 факториала. Это действительно номер, который там есть. 3 раза 2 раза 1. 6.
Теперь член четвертой степени, x до четвертой нет. x к пятому придет с плюсом. Так что от этого парня есть плюс. Это x для 0, 1, 2, 3, 4, 5. x для пятого. И что мне теперь делить? 5 факториал. 120. А потом минус и так далее. Минус x до седьмого факториала больше 7. Мы создали степенной ряд около 0, сосредоточив внимание на 0. И позвольте мне удалить это 1, потому что это просто пустая трата места.
x минус x в кубе. Все нечетные степени, и это потому, что синус x — нечетная функция. Если я перейду с x на минус x, все поменяет знак.
Что произойдет, если я подключу x, равное пи? Предположим, я взял x равным пи в этой формуле для синуса x. Эта бесконечная формула действует вечно.
Ну, я бы получил число пи минус пи в кубе больше 6 плюс пи до пятого больше 120. Это выглядело бы нелепо. Но мы с вами знаем, что ответ должен появиться. Правильный синус числа пи? 0.Я не планирую этого делать, но это должно сработать. Ладно, это синус. Это синус. И это странная серия.
Хорошо, хороший пример. Его близнец должен появиться здесь. Косинус. Какой ряд для косинуса? Это две серии, о которых стоит знать. Вы заметили здесь наклон 1, главное, что наклон синуса x в точке x равен 0, наклон равен 1. И у этого есть наклон 1.
Хорошо, а как насчет косинуса? Что ж, теперь я должен подключиться. Хорошо, косинус начинается здесь.Косинус минус синус минус косинус. Теперь моя f x будет косинусом x. И мне нужны его производные. У меня снова будут три строки, которые будут выглядеть точно так же, как эти три строки. Но они будут для косинуса. Итак, они начинаются с косинуса. Его производная минус синус. Его производная — минус косинус. Его производная какая? Плюс синус, затем косинус и навсегда минус синус. И позвольте мне подключиться сейчас, когда x равно 0. Это наша система. Найдите производные, подставьте 0. Итак, найдите производную в 0.
Ну, сама функция, 0-я производная равна 1. Первая производная равна 0. Вторая производная равна минус 1. Третья равна 0. Четвертая производная равна плюс 1, 0 и так далее. Это та же линия, что и у нас, но только начинается на 1. Начиная с косинуса.
Я знаю, какие производные мне нужны, теперь мне просто нужно создать свой ряд для косинуса x, который соответствует этим числам.
Еще раз. Просто сопоставьте эти числа с коэффициентами, которые я первоначально назвал a0, a1, a2, a3, но теперь у нас есть числа.
Хорошо, при x равно 0. Итак, как начинается этот ряд? Когда x равен 0, косинус 0 равен 1. Он начинается с 1. Это постоянный член, сидящий там. Коэффициент при x, линейный член равен 0. Поскольку косинус имеет наклон 0 в начале. Затем мы подходим к чему-то, что обнаруживается. Минус. Это будет … Что мы будем делать? Это константа, первая сила ушла. Вторая степень минус x в квадрате.
Но вы знаете, хочу ли я сопоставить вторую производную, чтобы она стала b минус 1.Сейчас это минус 2. Дифференциация дала бы мне 2x и 2. Так что мне нужно разделить на 2 или 2 факториала. Теперь все хорошо. Теперь она соответствует правильной второй производной минус 1. Тогда нет третьей производной. Четвертая производная равна плюс 1 x четвертому факториалу из четырех. А затем минус и так далее, x до шестого факториала над 6. Все четные полномочия, так что это четные полномочия. 0-я, вторая, четвертая, шестая степень. Так что это четная функция. Это означает, что косинус минус x в точности совпадает с косинусом x.Мы получаем небольшое представление об этих двух специальных группах, для которых синус является прекрасным примером нечетной функции, а косинус — прекрасным примером четной функции.
Ну, тут столько всего. Что будет, если я прерву серию? Я просто хочу взглянуть на эти первые термины, чтобы понять, что они представляют.
Предположим, я остановился здесь после линейного члена. Что у меня есть? Что это за х сам по себе? На самом деле это 0 плюс x, потому что из постоянного члена был 0.Это линейное приближение. Это дает мне уравнение касательной, y равно x, наклон 1.
Более интересно, отрезайте это. Отрежьте вот это. Это очень важная оценка. Это не точный косинус, потому что точный косинус есть у всех этих более поздних ребят. Но не забывайте, и я должен был сказать это с самого начала, эти n факториалов быстро растут. И все серии, о которых мы говорим, поскольку эти n факториалов растут так быстро, и я делю на них, я могу взять любой x и получить разумное число.
Если я возьму x равным пи, то эта серия синусов дала мне 0.
Что я получу, если вставлю x равно пи в ряд косинусов? Итак, ряд косинусов, если бы я подключил x к числу пи и набрался терпения, чтобы пойти довольно далеко, мои числа приблизились бы к косинусу числа пи. Что было бы минус 1. Я не вижу выхода минус 1. Вот 1 минус 1/2 числа пи в квадрате. Я не знаю, это примерно — 1/2 пи в квадрате может быть около 5 или около того. Но они сбивают друг друга. Они становятся очень маленькими, и мы получаем ответ минус 1.
Хорошо, это две важные серии, и теперь я должен рассказать вам о великой формуле Эйлера. Он связывает эти три серии, которые вы видели. Но чтобы установить эту связь, я должен ввести мнимое число i. Это нормально? Только представьте себе номер i. И все знают, что вы должны вообразить. Вы должны представить, что i в квадрате — это минус 1. И все мы знаем, что настоящего числа нет. Квадрат действительного числа всегда будет больше или равен 0. Итак, давайте просто создадим символ i с правилом, понимая, что каждый раз, когда мы видим квадрат i, я имею право написать минус 1.
ОК. Итак, какова великая формула Эйлера? Великая формула Эйлера, его блестящая идея заключалась в том, чтобы преобразовать x в этом e в ряд x, сделать x мнимым. Измените x на ix. Так что сделайте это мнимым числом. Так что могу я просто взять Эйлера, взять серию Тейлора или, может быть, Эйлера тоже, потому что эта буква е является его инициалом. Вероятно, так и было. Думаю, именно поэтому он нашел эту прекрасную связь.
Итак, если я возьму e в ix, а вместо x в этой серии я поставлю ix, просто сделайте это.Пусть x мнимый. Хорошо, могу я выписать серию 1 плюс — вместо x у меня ix. И тогда у меня есть 1 более 2 факториала ix в квадрате. И затем у меня есть 1 более 3 кубов факториала ix. И 1 по 4 факториала ix до четвертого. Это е к ix.
Хорошо, вы говорите, вы только что изменили x на ix. Это все, что я сделал. Теперь вот в чем дело.
Теперь я собираюсь взглянуть на этот беспорядок и отделить реальную часть от воображаемой. Я собираюсь разделить его на реальную и мнимую части.Так что же в этой штуке настоящего? Я вижу, что один, безусловно, реальное число. Вы видите другую, следующую, настоящую? Это происходит из этого я в квадрате. Квадрат я могу заменить на минус 1, совершенно реально. Итак, это минус от факториала i, возведенного в квадрат 1 над 2. x в квадрате все еще существует. В квадрате i было минус 1. Вот и все. А потом что-то пошло бы от i до четвертого. Потому что какое я до четвертого? Это я в квадрате минус 1 в квадрате. Мы вернемся к плюсу 1. Итак, плюс. Хороший.
Теперь идет часть, в которой есть «i» и единственная «i», с которой мне приходится жить.Так что i умножается на x. Теперь у меня есть кубик. Как мне работать с кубиком? i в кубе — это квадрат минус 1, умноженный на i. Я возведен в квадрат, умноженный на i, равен минус i. Так что у меня минус i. 1 над 3 факториалом и x в кубе и так далее.
Вы видите, что у нас есть? Вы понимаете, что это за настоящая часть от е до ix? Это косинус. Прямо там то же самое. Итак, я получаю косинус x для действительной части, а затем я умножаю эту серию. И вы можете увидеть, что это за серия. Это ряд синусов, x минус 1/6 x в кубе плюс 1/20 от x до пятого синуса x.Есть великая формула Эйлера, которая гласит, что е — ix … о, лучше я напишу ее на новой доске. Может, я просто напишу это здесь.
Я собираюсь скопировать с этой доски мою великую формулу Эйлера о том, что e – ix имеет действительную часть cos x. Мнимая часть дает мне синус x. И я это запишу. Теперь позволь мне поработать здесь. от e до ix равно cos x плюс i синус x. И я хочу нарисовать картинку. Хорошо, вот картинка.
На самом деле Эйлер часто писал свою формулу, или мы часто пишем его формулу, потому что берем косинусы и синусы.Как-то х не такой — это углы. Так что более естественно писать … Теперь, когда мы появились с синусами и косинусами, более естественно написать символ, который мы думаем как угол, такой как тета. Таким образом, вы чаще видели бы это таким образом. Я просто меняю буквы с х на тета, чтобы запомнить, что это угол. А сейчас нарисую.
Так что я должен это нарисовать. Хорошо, это реальное направление, а это воображаемое направление. Я просто иду, это настоящая часть. Я иду сюда, потому что тета.Итак, пусть это будет cos theta. А потом я иду вверх в воображаемом вверх или вниз. Итак, поперек — это реальная часть, а вверх / вниз — воображаемая часть. Скажите sine theta, я поднимаюсь. Эта высота — синус-тета, а этот угол — тета. Фантастика. Это картина формулы Эйлера. Что ж, это лучший способ увидеть это красивое заявление. И это изображение, чтобы напомнить нам. Мы бы сказали, что это комплексная плоскость, потому что точки состоят из двух частей: действительной и мнимой. В этом нет ничего сложного.
Теперь, прежде чем я остановлюсь, мы сделали три важных серии.Могу я упомянуть еще две, еще две из длинного списка возможностей? Одна из самых важных серий, где все коэффициенты равны единицам. Таким образом, все коэффициенты равны единицам. Это называется геометрической серией. Позвольте мне написать здесь его название. Это сериал Тейлора. Это силовой ряд. И функция, из которой оно происходит, оказывается 1 больше 1 минус x. Это функция.
И вы поймете, почему, если вы умножите обе части на 1 минус x, я получу 1 здесь. Если вы посмотрите, все будет отменено, кроме 1.Итак, это все.
Теперь есть существенная разница между этой серией и e до x. Самая большая разница в том, что мы больше не делим на факториал n. И в результате эти термины не обязательно становятся все меньше, меньше и меньше. Если x не ниже 1. Итак, мы в порядке, если x ниже 1. И x может быть отрицательным. Я даже могу сказать, что абсолютное значение x меньше 1, тогда эти члены станут меньше. Но при x, равном 1, мы мертвы. При x равно 1 у меня 1 плюс 1 плюс 1 плюс 1. Все единицы. Я получаю бесконечность.И с левой стороны я тоже получаю бесконечность. При x равняется 1 взрыву.
Хорошо, еще одна серия, и все готово. Еще один. Это аккуратный, потому что он вводит логарифм. Как я его получу? Я собираюсь начать с этой большой серии, геометрической. И я собираюсь взять интеграл каждого члена.
Итак, если я интегрирую 1, я получаю x. Если я интегрирую x, я получаю x в квадрате больше 2. Если я интегрирую x в квадрате, я получаю x куб больше 3. x четвертый больше 4 и так далее. Не 3-х факторный, а только 3-х.
И если я интегрирую это, что ж, позвольте мне записать ответ, а затем мы можем взять его производную и сказать: да, она дает это. Так что ответ отрицательный. Этот знак минус отображается здесь как минус логарифм 1 минус x. Потому что, если я возьму производную от этой функции, логарифм всегда помещает эту внутреннюю функцию вниз, а затем производную внутренней функции, цепное правило выводит минус 1, а минус 1 исчезает, и это красиво.
Так что просто посмотрите на эту серию, а затем на логарифм.Логарифм 1 минус x. Опять же, мы сопоставляем при x, равном 0. При x, равном 0, с этой функцией все в порядке. Фактически, если x равно 0, что это за функция? Логарифм 1, который равен 0, и нет постоянного члена. Хороший.
Хорошо, какие комментарии вы можете сказать по поводу этого последнего примера? Этот подходил для x меньше 1. Но затем он умер при x, равном 1.
Этому, ну, ему немного помогает деление на 3, 4 и 5. Но это ничтожная помощь. Это никак не сравнить с делением на 3 факториала, 4 факториала и т. Д., Которое действительно поможет.Так что, на самом деле, эта серия также хороша только тогда, когда x равно 1. Если x равно 1, она снова терпит неудачу. Что у меня есть при x, равном 1? Когда x равен 1, у меня логарифм 0 минус бесконечность. У меня бесконечность при x равно 1. При x, равном 1, это 1 плюс 1/2 плюс 1/3 плюс 1/4 плюс 1/5. Становится меньше, но не очень быстро и складывается до бесконечности. Так что есть целая дискуссия. Мы могли потратить часы на эту знаменитую серию, 1 плюс 1/2 плюс 1/3 плюс четверть и другие серии чисел. Я хотел заниматься исчислением, производными, интегралами, поэтому я взял функции и ряды степеней, а не ряд чисел, чтобы проиллюстрировать это.Хорошо. Спасибо.
ДИКТОР: Это продукт MIT OpenCourseWare и Gilbert Strang.
Финансирование этого видео было предоставлено Фондом лордов.
Чтобы помочь OCW продолжать предоставлять бесплатный и открытый доступ к курсам MIT, сделайте пожертвование на странице ocw.mit.edu/donate.
|