Цепь переменного тока с ёмкостью

Поскольку после того, как конденсатор зарядился полностью, он не пропускает через себя электрический ток, и поэтому идеальный конденсатор (ёмкость), установленный в цепи постоянного тока, обладает бесконечно большим сопротивлением.

Цепь переменного тока с ёмкостью

 

 

Если же произвести подключение конденсатора к источнику переменного тока, то процесс его заряда и разряда будет осуществляться непрерывно. Это означает, что через ёмкость будет проходить переменный электрический ток.

Ток i при условии включения в цепь переменного тока некоторой ёмкости будет определяется количеством электричества q, протекающего по этой цепи в единицу времени. Из этого следует, что:

где Δq – это изменение заряда q (то есть количества электричества) в течение времени Δt.

Что касается заряда q, который накоплен при изменениях напряжения u в конденсаторе, то он также подвержен непрерывному изменению, которое выражается формулой:

где Δu – это изменение напряжения u в течение промежутка времени Δt.

Та скорость, с которой изменяется напряжение (она выражается отношением Δu/Δt) будет иметь свои наибольшие значения тогда, когда угол ωt равняется 360°, 180° и 0°. Из этого следует, что значение тока i принимает свои наибольшие величины именно в эти моменты времени. Если же угол

ωt равняется 270° и 90°, то i = 0, поскольку скорость изменения напряжения Δu/Δt = 0.

Ток и напряжение в цепи переменного тока с ёмкостью

Ток заряда, который принято считать положительным, в цепи течет тогда, когда происходит заряд конденсатора, то есть на протяжение первой четверти периода. По мере того, как разница потенциалов на электродах ёмкости растет вследствие накопления ею электрического заряда, значение тока i падает. Когда

ωt = 90°, наступает полный заряд емкости, значение i = 0, а разность потенциалов между электродами конденсатора обретает то же самое значение, что и напряжение источника тока.

Значение тока i становится отрицательным тогда, когда он меняет свое направление. Это происходит тогда, когда ёмкость начинает разряжаться, то есть во второй четверти периода. Тогда, когда u = 0 а ωt = 180°, значение тока i становится максимальным. В этот же самый момент ток i начинает течь в обратном направлении (его принято считать отрицательным), начинается процесс перезарядки емкости, а полярность напряжения u источника также меняется на противоположную. Когда

ωt = 270° значение тока i становится равным нулю, и поэтому процесс заряда прекращается. После чего начинается разряд при первоначальном (то есть положительном) направлении тока.

Получается, что ёмкость и заряжается, и разряжается два раза на протяжении одного периода изменения напряжения. Из этого следует, что переменный ток i протекает в цепи непрерывно. Когда ёмкость включается в

цепь переменного тока, то ток i опережает напряжение u по фазе на угол, равный 90°. Можно также сказать, что напряжение u отстает по фазе от тока i на угол, равный 90°.

Емкостное сопротивление

Сопротивление, которое проявляет ёмкость к переменному току, носит название емкостного. Единицей измерения этой величины является Ом, а обозначается оно Х_с. Физическая природа емкостного сопротивления заключается в том, что оно обусловлено возникающей в конденсаторе ЭДС ес. Направление этой электродвижущей силы противоположно приложенному напряжению u, поскольку заряженная

ёмкость рассматривается в качестве источника, у которого между пластинами действует некоторая ЭДС ес. Именно она препятствует тому, чтобы под действием напряжения u происходило изменение тока, то есть оказывает определенное сопротивление его прохождению.

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt,    (26.8)

u = Uм sin (ϕ + ωt),    (26.9)

e = Ɛm sin (ψ + ωt).    (26.10)

Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле (16. 18):

R=(p₀l/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п.,

сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X_L, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

Х_L = ωL.              (26.11)

Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.

Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс.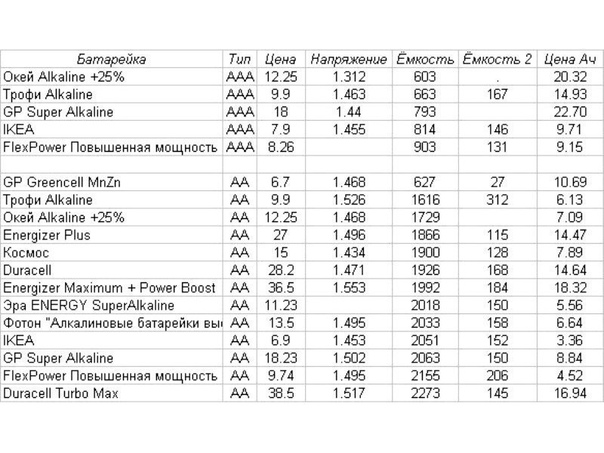

Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС.       (26.12)

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока.

Индуктивное X_L и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

X = X_L

—X_C        (26.13)

и имеет индуктивный характер при X_L > Хс и емкостный характер при X_L < Xc.

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.    (26.14)

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I²R.              (26.15)

Из (26. 14) видно, что для увеличения активной мощности переменного тока нужно повышать

cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при X_L=X_C.)

цепь переменного тока содержащая емкость индуктивность и сопротивление



цепь переменного тока содержащая емкость индуктивность и сопротивление

38)

ЦЕПЬ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ

Если в цепь постоянного, тока включить конденсатор (идеаль­ный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конден­сатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.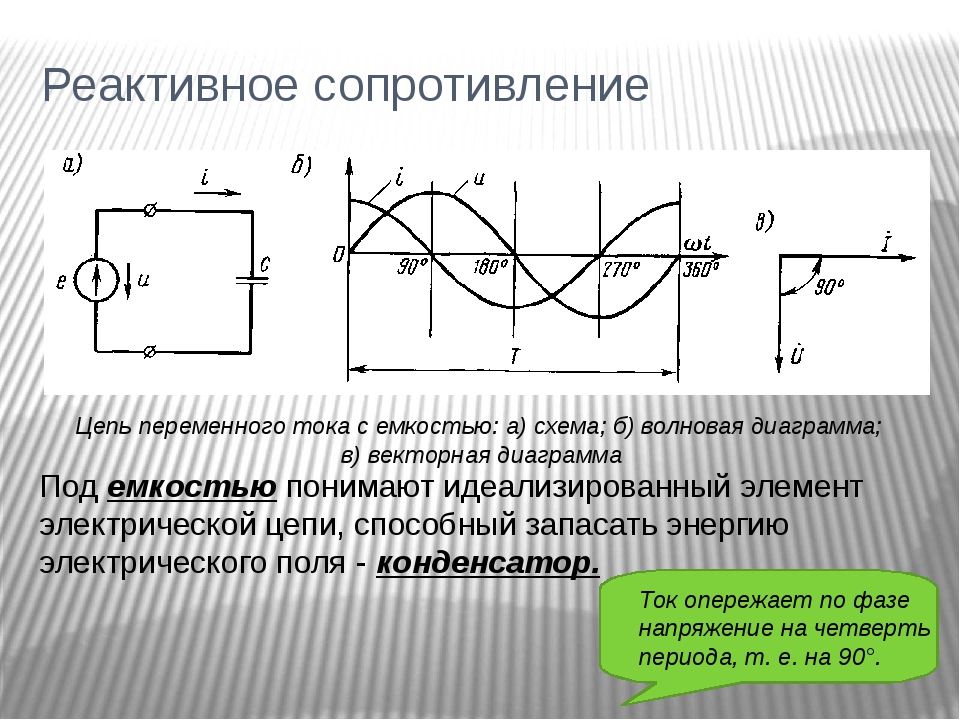

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

По мере накопления зарядов на обкладках конденсатора напря­жение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения  Um, напряжение конденсатора также станет равным Um, заряд конден­сатора прекращается и ток в цепи становится равным нулю. Ток в цепи конденсатора можно определить по формуле

где ∆q — количество электричества, протекающее по цепи за время ∆t.

 Из электростатики известно:

где   С — емкость конденсатора;

u — напряжение сети;

uc — напряжение конденсатора. Окончательно для тока имеем

Из последнего выражения видно, что, когда  ∆u/∆t   максимально (положения a, в, d),  i также максимально.

 

Когда  ∆u/∆t   = 0 (положения   б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшать­ся, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению Uc, приложенному к конденсатору, угловой частоте w и величине емкости конденсатора  C:

Обозначим

Величина Хс называется емкостным сопротивле­нием, или реактивным сопротивлением ем­кости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или   реактивной   слагающей   напряжения)   и   обозначается   Uc:

Емкостное сопротивление Хс, так же как индуктивное сопро­тивление xL, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет умень­шаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

при частоте 400 гц:

 

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Энергию, запасаемую конденсатором к моменту, когда напряже­ние на нем равно максимальному значению, можно определить по известной формуле CU2м/2.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии пов­торяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда wt = 45°, 135° и т. д.) достигает максимального значения, равного

 

Этой величиной принято характеризовать количественно про­цесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая,, что в рассматриваемой цепи U = IХc, получим сле­дующее выражение для реактивной мощности:

как определить напряжение, вольтаж конденсаторов

Конденсатор – один из самых важных элементов электрической цепи. Он накапливает внутри себя электрический заряд и передает его другим элементам электрической цепи. О том, что представляет собой конденсатор и как определить на нём напряжение, рассказывается ниже.

Что такое конденсатор

Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический –  из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Термин из учебного пособия

Характеристики конденсаторов

Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.

Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Емкость

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.

В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.

В чем измеряется напряжение конденсаторов

Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Измерение силы заряда двухполюсника

Что влияет на напряжение конденсаторов

Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.

Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.

Описание влияния на показатель

Как вычислить напряжение и вольтаж

Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.

Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.

Вычисление мультиметром

Формулы измерения напряжения конденсаторов

Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.

Основные формулы для расчета

В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.

Конденсатор в цепи переменного тока

Конденсатор в цепи переменного тока

Подробности

Просмотров: 549

«Физика — 11 класс»

Постоянный ток не может идти по цепи, содержащей конденсатор, так как обкладки конденсатора разделены диэлектриком.
Переменный же ток может идти по цепи, содержащей конденсатор.

Есть источники постоянного и переменного напряжений, в которых постоянное напряжение на зажимах источника равно действующему значению переменного напряжения.
Цепь состоит из конденсатора и лампы накаливания, соединенных последовательно.
При включении постоянного напряжения (переключатель влево) лампа не светится.
При включении переменного напряжения (переключатель вправо) лампа загорается, если емкость конденсатора достаточно велика.

Под действием переменного напряжения происходит периодическая зарядка и разрядка конденсатора.
Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Если сопротивлением проводов и обкладок конденсатора можно пренебречь,

то напряжение на конденсаторе равно напряжению на концах цепи.

Следовательно,

Заряд конденсатора меняется по гармоническому закону:

q = CU_m cos ωt

Сила тока, представляющая собой производную заряда по времени, равна:

Колебания силы тока опережают по фазе колебания напряжения на конденсаторе на .

Амплитуда силы тока равна:

I_m = U_mCω

Если ввести обозначение

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим

Величину Х_с, обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением.
Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.
Это и позволяет рассматривать величину Х_с как сопротивление конденсатора переменному току (емкостное сопротивление).

Чем больше емкость конденсатора, тем больше ток перезарядки.
Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.
В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х_с.
С увеличением емкости оно уменьшается.
Уменьшается оно и с увеличением частоты ω.

На протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля.
В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Итак,
сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на .

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Параметры аккумуляторов

Разрядные характеристики аккумуляторных батарей

Наиболее важными показателями качества АБ являются: емкость, напряжение, габариты, вес, стоимость, допустимая глубина разряда, срок службы, КПД, диапазон рабочих температур, допустимый ток заряда и разряда. Также, необходимо учитывать, что все характеристики производитель дает при определенной температуре – обычно 20 или 25 °С. При отклонениях от этого напряжения, характеристики меняются, и обычно в худшую сторону.

Значения напряжения и емкости обычно входят в название модели батареи. Например: RA12-200DG – батарея напряжением 12 вольт и емкостью 200 ампер*часов, гелевая, глубокого разряда. Это значит, что батарея может выдать в нагрузку энергию 12 х 200 = 2400 Вт*ч при 10 часовом разряде током в 1/10 от емкости. При больших токах и быстром разряде емкость батареи понижается. При меньших токах – обычно увеличивается. Это можно видеть на графике разрядных характеристик аккумуляторных батарей. Также, нужно смотреть на разрядные характеристики на конкретные батареи. Иногда производители в названии пишут завышенную емкость аккумулятора, которая имеет место только в идеальных условиях – так, например, делает Haze (у аккумуляторов Haze реальная емкость процентов на 10-20 ниже, чем указано в названии батареи).

При разряде током в 0,1 С время работы составляет 10 часов и батарея полностью выдаст в нагрузку аккумулированную энергию. При разряде током 2 С (в 20 раз большим) время работы будет около 15 минут (1/4 часа) и при этом батарея выдаст в нагрузку только половину аккумулированной энергии. При больших токах разряда это значение еще меньше. Зачастую в источниках бесперебойного питания аккумуляторные батареи работают в еще более тяжелых режимах, при которых токи разряда достигают 4 С. При этом время разряда сравнимо с 5 минутами и батарея выдает в нагрузку менее 40% энергии.

Емкость батареи

Количество энергии, которое может быть сохранено в батарее, называется ее емкостью. Она измеряется обычно в ампер-часах, хотя правильнее приводить значения в ватт-часах.

Заряд-разрядные кривые

Емкость (Вт*ч) = U*I*t

где U – напряжение аккумулятора, В; I – ток, который он может отдавать в течение времени t.

Так как обычно принимается, что для различных аккумуляторов напряжение одинаковое, то из формулы убирается напряжение, и остается емкость в ампер-часах.

Одна АБ емкостью 100 Ач может питать нагрузку током 1 А в течение 100 часов, или током 4 А в течение 25 часов, и т.п., хотя емкость батареи снижается при увеличении разрядного тока. На рынке продаются батареи емкостью от 1 до 3000 Ач.

Другие статьи Руководства

Для увеличения срока службы свинцово-кислотной АБ желательно использовать только малую часть ее емкости до повторной зарядки. Каждый процесс разряда-заряда называется зарядным циклом, причем не обязательно полностью разряжать аккумулятор. Например, если вы разрядили аккумулятор на 5 или 10% и затем снова зарядили его – это тоже считается как 1 цикл. Конечно, количество возможных циклов будет сильно отличаться при различной глубине разряда (см. ниже). Если возможно использовать более 50% энергии, запасенной в АБ до ее заряда, без заметного ухудшения ее параметров, такая батарея называется батареей “глубокого разряда”.

Можно повредить батареи, если перезарядить их. Максимальное напряжение синцово-кислотных АБ должно быть 2,5 вольта на элемент, или 15 В для 12-ти вольтовой батареи. Многие фотоэлектрические батареи имеют мягкую нагрузочную характеристику, поэтому при увеличении напряжения ток заряда снижается значительно. Поэтому всегда необходимо использовать специальный контроллер заряда для солнечных батарей. В случае применения ветроэлектрических станций или микроГЭС, такие контроллеры также обязательны.

Напряжение

Напряжение на аккумуляторе зачастую является основным параметром, по которому можно судить о состоянии и степени заряженности аккумулятора. Особенно это относится к герметизированным аккумуляторам, у которых не возможно измерить плотность электролита.

Напряжение при заряде, разряде и отсутствии тока очень сильно отличаются. Для определения степени заряженности аккумулятора измеряют напряжение на его клеммах при отсутствии как зарядного, так и разрядного токов в течение как минимум 3-4 часов. За это время напряжение обычно успевает стабилизироваться. Значение напряжения при заряде или разряде ничего не скажет от состоянии или степени заряженности АБ. Примерная зависимость степени заряженности аккумулятора от напряжения на его клеммах в режиме холостого хода, приведена в таблице ниже. Это типичные значения для стартерных аккумуляторов с жидким электролитом. Для герметизированных аккумуляторов (AGM и гелевых) обычно эти напряжения немного выше (нужно запрашивать производителя) – например, AGM батареи полностью заряжены, если напряжение составляет 13-13,2В (сравните с напряжением стартерных батарей с жидким электролитом 12,5-12,7В).

Степень заряженности

Степень заряженности зависит от очень многих факторов, и точно ее могут определить только специальные зарядные устройства с памятью и микропроцессором, которые отслеживают как заряд, так и разряд конкретного аккумулятора в течение нескольких циклов. Этот метод наиболее точный, но и наиболее дорогой. Однако он сможет сэкономить много денег при обслуживании и замене аккумуляторов. Применение специальных устройств, контролирующих работу аккумуляторов по степени их заряженности, позволяет очень сильно повысить срок службы свинцово-кислотных аккумуляторов. Ряд предлагаемых нами контроллеров для солнечных батарей имеют встроенные устройства вычисления степени заряженности аккумулятора и регулируют заряд в зависимости от ее величины.

Для определения степени заряженности можно использовать также следующие 2 упрощенных метода.

1. Напряжение на аккумуляторе. Этот способ наименее точный, но требует только наличия цифрового вольтметра, способного измерять десятые и сотые доли вольта. Перед измерениями нужно отсоединить от аккумулятора всех потребителей и все зарядные устройства и подождать как минимум 2 часа. Затем можно измерить напряжение на терминалах аккумулятора. Ниже в таблице приведены напряжения для аккумуляторов с жидким электролитом. Для полностью заряженной новой AGM или гелевой батареи напряжение составляет 13-13,2В (сравните с напряжением стартерных батарей с жидким электролитом 12,5-12,7В). По мере старения аккумуляторов это напряжение снижается. Можно измерять напряжение на каждой банке аккумулятора, чтобы найти неисправную банку (разделите напряжение для 12В на 6 для того, чтобы определить нужное напряжение на одной банке).
2. Второй метод определения степени заряженности – по плотности электролита. Этот метод подходит только для аккумуляторов с жидким электролитом.

Также, нужно подождать 2 часа перед измерениями. Для измерения используется ареометр. Обязательно наденьте резиновые перчатки и защитные очки! Держите рядом пищевую соду и воду на случай, если вода попадет на кожу.

Степень заряженности	Батарея 12В	Батарея 24 В	Плотность электролита
100	12.70	25.40	1.265
95	12.64	25.25	1.257
90	12.58	25.16	1.249
85	12.52	25.04	1.241
80	12.46	24.92	1.233
75	12.40	24.80	1.225
70	12.36	24.72	1.218
65	12.32	24.64	1.211
60	12.28	24.56	1.204
55	12.24	24.48	1.197
50	12.20	24.40	1.190
40	12.12	24.24	1.176
30	12.04	24.08	1.162
20	11.98	23.96	1.148
10	11.94	23.88	1.134

Срок службы аккумуляторов 

[sociallocker id=”1616″] Срок службы аккумуляторных батарей в циклах

Неправильно определять срок службы аккумуляторов в годах или месяцах. Срок службы батареи определяется числом циклов заряд-разряд и значительно зависит от условий ее эксплуатации. Чем глубже разряжается батарея, чем большее время она находится в разряженном состоянии, тем меньшее число возможных циклов работы.

Само понятие «количество рабочих циклов «заряда-разряда» аккумулятора» относительное, так как сильно зависит от различных факторов. Кроме того, значение количества рабочих циклов, например для одного типа аккумулятора, не является универсальным понятием, так как зависит от технологии, различной у каждого из производителей.Срок службы аккумуляторов определяется в циклах, поэтому время работы в годах – приблизительное и рассчитано для типичных условий работы. Поэтому, если, например, в рекламе указано, что срок службы аккумуляторов составляет 12 лет, это значит, что производитель посчитал срок службы для буферного режима с средним числом циклов заряд-разряд 8 в месяц. Например, для AGM аккумуляторов Haze указывается срок службы 12 лет и максимальное число циклов 1200 при разряде на 20%. В год получается 100 таких циклов, в месяц – около 8.

Еще один важный момент – в процессе эксплуатации полезная емкость аккумулятора уменьшается. Все характеристики по количеству циклов обычно приводятся не до полной смерти аккумулятора, а до момента потери им 40% своей номинальной емкости. Т.е, если производителем приведено количество циклов 600 при 50% разряде, это значит, что через 600 идеальных циклов (т.е. при температуре 20С и разряде током одной величины, обычно 0,1С) полезная емкось аккумулятора будет 60% от начальной. При такой потере емкости уже рекомендуется замена аккумулятора.

Свинцово-кислотные АБ, предназначенные для использования в системах автономного электроснабжения имеют, срок службы от 300 до 3000 циклов в зависимости от типа и глубины разряда. В системах на базе ВИЭ батарея может разрядиться гораздо сильнее, чем при буферном режиме. Для обеспечения длительного срока службы, в типичном цикле разряд не должен превышать 20-30% емкости АБ, а глубокий разряд – не более 80% емкости. Очень важно сразу же после разряда заряжать свинцово-кислотные аккумуляторы. Длительное нахождение (более 12 часов) в разряженном или не полностью заряженном состоянии приводит к необратимым последствиям в аккумуляторах и снижению их срока службы.

[/sociallocker]

Как определить, что аккумулятор уже близок к окончанию своего срока службы? Очень просто – у аккумулятора повышается внутреннее сопротивление, это приводит к более быстрому росту напряжения при заряде (и, соответственно, снижению времени, требуемого для заряда), и более быстрому разряду аккумулятора. Если заряд производится током, близким к предельно допустимому, умирающий аккумулятор будет нагреваться при заряде сильнее, чем раньше.

Максимальные токи заряда и разряда

Токи заряда и разряда любой аккумуляторной батареи измеряются относительно ее емкости. Обычно для аккумуляторов максимальный ток заряда не должен превышать 0,2-0,3С. Превышение зарядного тока ведет к сокращению срока службы аккумуляторов. Мы рекомендуем устанавливать максимальный ток заряда не более 0,15-0,2С. Смотрите характеристики на конкретные модели аккумуляторов для определения максимального зарядного и разрядного токов.

Саморазряд

Явление саморазряда характерно в большей или меньшей степени для всех типов аккумуляторов и заключается в потере ими своей емкости после того, как они были полностью заряжены в отсутствие внешнего потребителя тока.

Для количественной оценки саморазряда удобно использовать величину потерянной ими за определенное время емкости, выраженную в процентах от значения, полученного сразу после заряда. За промежуток времени, как правило, принимается интервал времени, равный одним суткам и одному месяцу. Так, например, для исправных NiCD аккумуляторов считается допустимым саморазряд до 10% в течение первых 24 часов после окончании заряда, для NiMH – немного больше, а для Li-ION пренебрежимо мал и оценивается за месяц. Саморазряд в герметизированных свинцово-кислотных аккумуляторах значительно уменьшен и составляет 40% в год при 20 °С и 15% при 5 °С. При более высоких температурах хранения саморазряд увеличивается: при 40 °С батареи лишаются 40 % емкости за 4-5 месяцев.

Следует отметить, что саморазряд аккумуляторов максимален именно в первые 24 часа после заряда, а затем значительно уменьшается. Глубокий его разряд и последующий заряд увеличивают ток саморазряда.

Саморазряд аккумуляторов в основном обусловлен выделением кислорода на положительном электроде. Этот процесс еще больше усиливается при повышенной температуре. Так, при повышении окружающей температуры на 10 градусов по отношению с комнатной возможно увеличение саморазряда в два раза.

В некоторой степени саморазряд зависит от качества использованных материалов, технологического процесса изготовления, типа и конструкции аккумулятора. Потери емкости могут быть вызваны повреждением сепаратора, когда образования слипшихся кристаллов пробивают его. Сепаратором принято называть тонкую пластину, разделяющую положительный и отрицательный электроды. Это обычно происходит из–за неправильного обслуживания аккумулятора, его отсутствия или применения несоответствующих или некачественных зарядных устройств. У изношенного аккумулятора пластинки электродов разбухают, слипаясь друг с другом, что приводит к повышению тока саморазряда, при этом поврежденный сепаратор невозможно восстановить проведением циклов заряда/разряда.

Каргиев Владимир, “Ваш Солнечный Дом”
©При цитировании ссылка на эту страницу и на “Ваш Солнечный Дом” обязательна

Дополнительная информация по теме в Разделе “Библиотека“. Настоятельно рекомендуем почитать эту статью

ГЛОССАРИЙ

Емкость (С) – энергия, которую способен отдать аккумулятор в нагрузку, выражаемая в ампер-часах (А·ч, мA·ч). Она будет больше при следующих условиях: меньшем токе разряда, разряде с меньшими перерывами, более высокой температуре окружающей среды, а также более низком конечном напряжении.

Номинальная емкость – номинальное значение емкости: количество энергии, которую способен отдать полностью заряженный аккумулятор при разряде в строго определенных условиях.

Саморазряд – потеря емкости в отсутствие внешнего потребителя тока.

Срок службы батареи – наработка, при которой разрядная емкость сделается меньше определенной нормированной величины, обычно оценивается рабочим количеством циклов “заряд-разряд”.

Срок хранения – максимальный период времени, в течение которого батарея может храниться при оговоренных условиях, не требуя дополнительной зарядки.

Эта статья прочитана 123828 раз(а)!

Продолжить чтение

Конденсаторы и цепи переменного тока

ОСНОВЫ ЭЛЕКТРОНИКИ

Конденсаторы и цепи переменного тока

Коль скоро мы начинаем рассматривать изменяющиеся сигналы напряжения и тока, нам необходимо познакомиться с двумя очень занятными элементами, которые не находят применения в цепях постоянного тока, — речь идет о конденсаторах и индуктивностях. Скоро вы убедитесь, что эти компоненты вместе с резисторами являются основными элементами пассивных линейных цепей, составляющих основу почти всей схемотехники. Особенно следует подчеркнуть роль конденсаторов — без них не обходится почти ни одна схема. Они используются при генерации колебаний, в схемах фильтров, для блокировки и шунтирования сигналов. Их используют в интегрирующих и дифференцирующих схемах. На основе конденсаторов и индуктивностей строят схемы формирующих фильтров для выделения нужных сигналов из фона. Некоторые примеры подобных схем вы найдете в этой главе, а еще большее число интересных примеров использования конденсаторов и индуктивностей встретится вам в последующих главах.

Приступим к более детальному изучению конденсаторов. Явления, протекающие в конденсаторе, описываются математическими зависимостями, поэтому читателям, которые имеют недостаточную подготовку в области математики, полезно прочитать приложение Б. Не огорчайтесь, если некоторые детали не будут сразу вполне понятны, главное — это общее понимание вопроса.

1.12. Конденсаторы

Конденса рис. 1.27. -это устройство, имеющее два вывода и обладающее следующим свойством:

Q = CU

Конденсатор, имеющий емкость С фарад, к которому приложено напряжение U вольт, накапливает заряд Q кулон на одной пластине и — Q на другой.

Рис. 1.27. Конденсатор.

В первом приближении конденсаторы — это частотно-зависимые резисторы. Они позволяют создавать, например, частотно-зависимые делители напряжения. Для решения некоторых задач (шунтирование, связывание контуров) больших знаний о конденсаторе и не требуется, другие задачи (построение фильтров, резонансных схем, накопление энергии) требуют более глубоких знаний. Например, конденсаторы не рассеивают энергию, хотя через них и протекает ток, — дело в том, что ток и напряжение на конденсаторе смещены друг относительно друга по фазе на 90°.

Продифференцировав выражение для Q (см. приложение Б), получим

I = C(dU/dt).

Итак, конденсатор — это более сложный элемент, чем резистор; ток пропорционален не просто напряжению: а скорости изменения напряжения. Если напряжение на конденсаторе, имеющем емкость 1 Ф, изменится на 1 В за 1 с, то получим ток 1 А. И наоборот, протекание тока 1 А через конденсатор емкостью 1 Ф вызывает изменение напряжения на 1 В за 1 с. Емкость, равная одной фараде, очень велика, и поэтому чаще имеют дело с микрофарадами (мкФ) или пикофарадами (пФ). Для того чтобы сбить с толку непосвященных, на принципиальных схемах иногда опускают обозначения единиц измерения. Их приходится угадывать из контекста. Например, если подать ток 1 мА на конденсатор емкостью 1 мкФ, то напряжение за 1 с возрастет на 1000 В. Импульс тока продолжительностью 10 мс вызовет увеличение напряжения на конденсаторе на 10 В (рис. 1.28).

Рис. 1.28. Напряжение на конденсаторе изменяется, когда через него протекает ток.

Промышленность выпускает конденсаторы разнообразных форм и размеров, через некоторое время вы познакомитесь с наиболее распространенными представителями этого обширного семейства. Простейший конденсатор состоит из двух проводников, расположенных на небольшом расстоянии друг от друга (но не соприкасающихся между собой), настоящие простейшие конденсаторы имеют именно такую конструкцию. Чтобы получить большую емкость, нужны большая площадь и меньший зазор между проводниками, обычно для этого один из проводников покрывают тонким слоем изолирующего материала (называемого диэлектриком), для таких конденсаторов используют, например, алитированную (покрытую алюминием) майларовую пленку. Широкое распространение получили следующие типы конденсаторов: керамические, электролитические (изготовленные из металлической фольги с оксидной пленкой в качестве изолятора), слюдяные (изготовленные из металлизированной слюды). Каждому типу конденсаторов присущи свои качества, краткий перечень отличительных особенностей каждого типа конденсаторов приведен мелким шрифтом в разделе «Конденсаторы». В общем можно сказать, что для некритичных схем подходят керамические и майларовые конденсаторы, в схемах, где требуется большая емкость, применяются танталовые конденсаторы, а для фильтрации в источниках питания используют электролитические конденсаторы.

Параллельное и последовательное соединение конденсаторов. Ёмкость нескольких параллельно соединенных конденсаторов равна сумме их емкостей. Нетрудно в этом убедиться: приложим напряжение к параллельному соединению, тогда:

CU = Q = Q₁ + Q₂ + Q₃ + … =

= С₁U + C₂U + C₃U + … =

= (C₁ + C₂ + C₃ + …)U

или

C = C₁ + C₂ + C₃ + …

Для последовательного соединения конденсаторов имеем такое же выражение, как лдя параллельного соединения резисторов:

C = 1/1/C₁ + 1/C₂ + 1/C₃.

В частном случае для двух конденсаторов:

C = C₁C₂/(C₁ + C₂).

Ток, заряжающий конденсатор (I = CdU/dt),обладает некоторыми особыми свойствами. В отличие от тока, протекающего через резистор, он пропорционален не напряжению, а скорости изменения напряжения (т.е. его производной по времени).Далее, мощность (U умноженное на I), которая связана с протекающим через конденсатор током, не обращается в тепло, а сохраняется в виде энергии внутреннего электрического поля в конденсаторе. При разряде конденсатора происходит извлечение энергии. Эти занятные свойства мы рассмотрим с другой точки зрения, когда будем изучать реактивность (начиная с разд. 1.18.).

КОНДЕНСАТОРЫ

Промышленностью выпускается много типов конденсаторов. Здесь перечислены основные преимущества и недостатки различных типов. Очевидно, что данная оценка имеет несколько субъективный характер (см. таблицу).

Тип	Диапазон емкости	Макс. U	Точность	Термо-стаб.	Утечка	Примечание
Слюдяной	1пФ- 0,01мкФ	100-600	Хорошая		Малая	Очень хорошие: рекомендуются для радиочастот
Цилиндри- ческин керамический	0,5пФ- 100пФ	100-600		Варьирует		Несколько значений температурного коэффициента, включая 0
Керамический	10пФ- 1мкФ	50- 30000	Низкая	Низкая	Средняя	Малые габариты, недороги, широко используются
Полиэфирные (маяларовые)	0,001мкФ- 50мкФ	50-600	Хорошая	Низкая	Малая	Хорошие, недорогие, широко используются
Полисти- ролвые	10 пФ- 2.7мкФ	100-600	Отличная	Высокая	Очень малая	Высоко- качестенные, крупногабаритные, рекомендуются для фильтров
Поликар- боватные	10ОпФ- ЗОмкФ	50-800	Отличная	Отличная	Малая	Высоко- качественные имеют малые габариты
Полипро- пиленовые	100пФ- 50мкФ	100-800	Отличная	Высокая	Очень малая	Высоко- качественные; низкое диэлектрическое поглощение
Тефлоновые	100 пФ- 2мкФ	50-200	Отличная	Отличная	Самая малая	Высоко- качественные, самое низкое диэлектрическое поглощение
Стеклянные	10 пФ- 1000мкФ	100-600	Хорошая		Очень малая	Стабильны при длительной эксплуатации
Фарфоровые	100 пФ- 0,1мкФ	50-400	Хорошая	Высокая	Малая	Хорошие: стабильные при длительной эксплуатации
Танталовые	0.1мкФ- 500мкФ	6-100	Низкая	Низкая		Большая емкость; поляризованные; малогабаритные; небольшая индуктивность
Электро- литаческие	0,1мкФ- 1,6Ф	3-600	Хуже не бывает	Хуже не бывает	Ужасная	Фильтры источников питания; поляризованные; короткий срок службы
С двойным слоем диэлектрика	0,1Ф- 10Ф	1,5-6	Низкая	Низкая	Малая	Поддержка памяти; высокое последовательное сопротивление
Масляные	0,1мкФ- 20мкФ	200- 10000			Малая	Высоковольтные фильтры; крупногабаритные, длительный срок службы
Вакуумные	1пФ- 5000пФ	2000- 36000			Очень малая	Передатчики

Упражнение 1.12. Получите выражение для емкости двух последовательно соединенных конденсаторов. Подсказка: так как точка соединения конденсаторов не имеет внешних подключений, то заряд, накопленный двумя конденсаторами, должен быть одинаков.

Индуктивности и трансформаторы

Формула емкости тока напряжения конденсатора

Формула емкости напряжения тока конденсатора очень важна для нас. Это самый основной пассивный элемент в электрической цепи.

Пока что мы ограничились изучением резистивных цепей. В этом посте мы представим два новых и важных элемента пассивной линейной цепи: конденсатор и катушку индуктивности. В отличие от резисторов, которые рассеивают энергию, конденсаторы и катушки индуктивности не рассеивают, а накапливают энергию, которую можно получить позже.По этой причине конденсаторы и катушки индуктивности называются накопительными элементами.

Применение резистивных цепей весьма ограничено. С введением конденсаторов и катушек индуктивности в этом посте мы сможем проанализировать более важные и практичные схемы.

Мы начнем с знакомства с конденсаторами и описания их последовательного или параллельного соединения. Позже мы проделаем то же самое с индукторами. В качестве типичных приложений мы исследуем, как конденсаторы сочетаются с операционными усилителями для формирования интеграторов, дифференциаторов и аналоговых компьютеров.

Конденсатор Напряжение Ток Формула емкости

Конденсатор — это пассивный элемент, предназначенный для хранения энергии в своем электрическом поле. Помимо резисторов, конденсаторы являются наиболее распространенными электрическими компонентами. Конденсаторы широко используются в электронике, коммуникациях, компьютерах и энергосистемах. Например, они используются в схемах настройки радиоприемников и в качестве элементов динамической памяти в компьютерных системах.

Конденсатор обычно имеет конструкцию, показанную на рисунке.(1).

Рисунок 1. Типичный конденсатор.

Конденсатор состоит из двух проводящих пластин, разделенных изолятором (или диэлектриком).

Во многих практических приложениях пластины могут быть из алюминиевой фольги, а диэлектрик может быть из воздуха, керамики, бумаги или слюды.

Когда источник напряжения v подключен к конденсатору, как показано на рисунке (2), источник накапливает положительный заряд q на одной пластине и отрицательный заряд — q на другой.

Рисунок 2. Конденсатор с приложенным напряжением v.

Говорят, что конденсатор хранит электрический заряд. Количество накопленного заряда, представленное q , прямо пропорционально приложенному напряжению v , так что

(1)

, где C , константа пропорциональности, называется емкостью конденсатора. Единица измерения емкости — фарад (Ф) в честь английского физика Майкла Фарадея (1791–1867). Из уравнения (1) можно вывести следующее определение.

Емкость — это отношение заряда на одной пластине конденсатора к разности напряжений между двумя пластинами, измеряемое в фарадах (Ф).

Обратите внимание на уравнение (1), что 1 фарад = 1 кулон / вольт.

Хотя емкость конденсатора C представляет собой отношение заряда q на пластину к приложенному напряжению v , она не зависит от q или v . Это зависит от физических размеров конденсатора.Например, конденсатор с параллельными пластинами, показанный на рисунке. (1), емкость определяется как

(2)

, где A, — площадь поверхности каждой пластины, d — расстояние между пластинами и ϵ . — диэлектрическая проницаемость диэлектрического материала между пластинами. Хотя уравнение (2) применимо только к конденсаторам с параллельными пластинами, мы можем сделать вывод, что, как правило, значение емкости определяют три фактора:

1. Площадь поверхности пластин — чем больше площадь, тем больше емкость.
2. Расстояние между пластинами — чем меньше расстояние, тем больше емкость.
3. Диэлектрическая проницаемость материала — чем выше диэлектрическая проницаемость, тем больше емкость.

Конденсаторы доступны в продаже в различных номиналах и типах. Обычно конденсаторы имеют значения в диапазоне от пикофарад (пФ) до микрофарад ( мк Ф). Они описываются диэлектрическим материалом, из которого они сделаны, а также фиксированным или переменным типом.На рисунке (3) показаны условные обозначения для конденсаторов постоянной и переменной емкости.

Рис. 3. Обозначения схем конденсаторов: (а) конденсатор постоянной емкости, (б) конденсатор переменной емкости.

Обратите внимание, что согласно соглашению о пассивных знаках, если v > 0 и i > 0 или если v <0 и i <0, конденсатор заряжается, и если v · i <0, конденсатор разряжается.

На рисунке (4) показаны распространенные типы конденсаторов постоянной емкости.Конденсаторы из полиэстера легкие, стабильные, и их изменение с температурой предсказуемо. Вместо полиэстера можно использовать другие диэлектрические материалы, такие как слюда и полистирол. Пленочные конденсаторы скручиваются и помещаются в металлические или пластиковые пленки. Электролитические конденсаторы обладают очень высокой емкостью.

Рис. 4. Конденсаторы постоянной емкости: (а) полиэфирный конденсатор, (б) керамический конденсатор, (в) электролитический конденсатор.

На рисунке (5) показаны наиболее распространенные типы переменных конденсаторов. Емкость подстроечного (или подстроечного) конденсатора часто размещается параллельно с другим конденсатором, так что эквивалентная емкость может быть немного изменена.

Рис. 5. Конденсаторы переменной емкости: (а) подстроечный конденсатор, (б) подстроечный конденсатор.

Емкость переменного воздушного конденсатора (сетчатые пластины) изменяют поворотом вала. В радиоприемниках используются переменные конденсаторы, позволяющие настраиваться на разные станции. Кроме того, конденсаторы используются для блокировки постоянного тока, пропускания переменного тока, сдвига фазы, накопления энергии, запуска двигателей и подавления шума.

Чтобы получить отношение тока к напряжению конденсатора, мы берем производную от обеих сторон уравнения.(1). Так как

(3)

, дифференцируя обе стороны уравнения (1), получаем

(4)

Это соотношение тока и напряжения для конденсатора, предполагая пассивное соглашение о знаках. Это соотношение показано на рисунке (6) для конденсатора, емкость которого не зависит от напряжения.

Рисунок 6. Вольт-амперная зависимость конденсатора. Конденсаторы

, удовлетворяющие уравнению (4), называются линейными . Для нелинейного конденсатора график зависимости тока от напряжения не является прямой линией.Хотя некоторые конденсаторы нелинейны, большинство из них линейны. В этом посте мы будем использовать линейные конденсаторы.

Зависимость напряжения от тока конденсатора может быть получена путем интегрирования обеих сторон уравнения (4). Получаем

(5)

или

(6)

, где v ( t ₀ ) = q ( t ₀ ) / C — напряжение на конденсаторе в момент времени т ₀ . Уравнение (6) показывает, что напряжение конденсатора зависит от прошлой истории тока конденсатора.Следовательно, конденсатор имеет память — свойство, которое часто используется.

Мгновенная мощность, подаваемая на конденсатор, составляет

(7)

Таким образом, энергия, запасенная в конденсаторе, равна

(8)

. Отметим, что v (−∞) = 0, поскольку конденсатор не был заряжен при t = −∞. Таким образом,

(9)

Используя уравнение (1), мы можем переписать уравнение (9) как

(10)

Уравнения. (9) или (10) представляют энергию, запасенную в электрическом поле, которое существует между пластинами. конденсатора.Эту энергию можно получить, поскольку идеальный конденсатор не может рассеивать энергию. Фактически, слово конденсатор происходит от способности этого элемента накапливать энергию в электрическом поле.

Следует отметить следующие важные свойства конденсатора:

1. Обратите внимание на уравнение (4), что, когда напряжение на конденсаторе не изменяется со временем (т. Е. Постоянное напряжение), ток через конденсатор равен нулю. . Таким образом,

А конденсатор является обрывом цепи постоянного тока.

Однако, если батарея (напряжение постоянного тока) подключена к конденсатору, конденсатор заряжается.

2. Напряжение на конденсаторе должно быть постоянным.

Напряжение на конденсаторе не может резко измениться.

Конденсатор сопротивляется резкому изменению напряжения на нем. Согласно уравнению (4) для скачкообразного изменения напряжения требуется бесконечный ток, что физически невозможно. Например, напряжение на конденсаторе может иметь форму, показанную на рисунке.(7a), тогда как напряжение на конденсаторе физически не может принимать форму, показанную на рисунке (7b), из-за резких изменений. И наоборот, ток через конденсатор может мгновенно измениться.

Рис. 7. Напряжение на конденсаторе: (а) разрешено, (б) недопустимо; резкое изменение невозможно.

3. Идеальный конденсатор не рассеивает энергию. Он забирает энергию из схемы при хранении энергии в своем поле и возвращает ранее сохраненную энергию при подаче энергии в схему.

4. Реальный неидеальный конденсатор имеет сопротивление утечки, соответствующее параллельной модели, как показано на рисунке (8). Сопротивление утечки может достигать 100 МОм, и им можно пренебречь в большинстве практических приложений. По этой причине в этом посте мы будем предполагать идеальные конденсаторы.

Рис. 8. Принципиальная схема неидеального конденсатора.

Конденсатор Напряжение Ток Емкость Примеры формул

1. (a) Рассчитайте заряд, накопленный на конденсаторе емкостью 3 пФ при 20 В на нем. (б) Найдите энергию, запасенную в конденсаторе.

Решение:
(a) Начиная с q = C v,

(b) Запасенная энергия составляет

2. Напряжение на конденсаторе 5- μ F составляет

v ( t ) = 10 cos 6000 t V

Рассчитайте ток через него.

Решение:
По определению, ток равен

3. Определите напряжение на конденсаторе 2- мк F, если ток через него равен
i ( t ) = 6 e ^{−3000 t} мА
Предположим, что начальное напряжение конденсатора равно нулю.

Решение:
Начиная с

, затем

4. Определите ток через конденсатор емкостью 200- мкМ Ф с напряжением

Рис. 9

, показанный на рис. (9).

Решение:
Форма волны напряжения может быть описана математически как

Так как i = C d v / dt и C = 200 μ F, берем производную из v , чтобы получить

Таким образом, текущая форма волны такая, как показано на рисунке.(10).

Рисунок 10

5. Получите энергию, запасенную в каждом конденсаторе, показанном на рисунке (11a), в условиях постоянного тока
.

Рисунок 11

Решение:
В условиях постоянного тока мы заменяем каждый конденсатор с разомкнутой цепью, как показано на рисунке. (11b). Ток через последовательную комбинацию резисторов 2 кОм и 4 кОм получается делением тока как

Следовательно, напряжения v ₁ и v ₂ на конденсаторах равны

и в них хранятся энергии

Зарядка и разрядка конденсатора от d.c. источник — Конденсаторы — Высшая физика. Редакция

Показанная схема используется для исследования заряда и разряда конденсатора. Источник имеет незначительное внутреннее сопротивление.

Конденсатор изначально не заряжен. Когда переключатель перемещается в положение \ (1 \), электроны перемещаются от отрицательного вывода источника питания к нижней пластине конденсатора. Этому движению заряда противодействует резистор \ (R \), поэтому начальный ток в цепи равен \ (I = \ frac {E} {R} \)

Зарядка

Во время зарядки конденсатора:

• зарядный ток уменьшается от начального значения \ (\ frac {E} {R} \) до нуля
• разность потенциалов на пластинах конденсатора увеличивается от нуля до максимального значения \ (E \), когда конденсатор полностью заряжен
• все время сумма разности потенциалов на конденсаторе и разности потенциалов на резисторе равна ЭДС источника питания
• разности потенциалов на резисторе (определяется как \ ({V_R} = IR \ )) уменьшается от начального значения \ (E \) до нуля, когда конденсатор полностью заряжен

Когда переключатель перемещается в положение \ (2 \), электроны перемещаются от нижней пластины через резистор к верхней пластине. конденсатора.

Электроны через амперметр движутся в направлении, противоположном зарядке.

Разрядка

Во время разряда конденсатора:

• ток разряда уменьшается от начального значения \ (- \ frac {E} {R} \) до нуля
• разность потенциалов на пластинах конденсатора уменьшается с \ (E \) до нуля, когда конденсатор полностью разряжен
• , разность потенциалов на конденсаторе всегда равна разности потенциалов на резисторе
• разности потенциалов на резисторе (определяется как \ ({V_R} = IR \)) уменьшается от начального значения \ (E \) до нуля, когда конденсатор полностью разряжен

Элементы электронной схемы — Обзор MCAT

Элементы схемы Ток (I = ΔQ / Δt, условные обозначения, единицы) Ток — это скорость прохождения заряда через поперечное сечение проводника (провода). Традиционно направление тока принимается за поток положительных зарядов. Единица измерения тока — кулоны в секунду, Кл / с. Аккумулятор, электродвижущая сила, напряжение Электродвижущая сила (ЭДС) на самом деле не сила, а разность потенциалов с единичным напряжением. Аккумулятор является источником ЭДС. Если аккумулятор не имеет внутреннего сопротивления, то разность потенциалов на аккумуляторе = ЭДС. Если батарея имеет внутреннее сопротивление, то разность потенциалов на батарее = ЭДС — падение напряжения из-за внутреннего сопротивления. Клеммный потенциал, внутреннее сопротивление аккумулятора Потенциал клемм — это напряжение на клеммах аккумулятора. Внутреннее сопротивление батареи похоже на резистор рядом с батареей, подключенной последовательно. Клеммный потенциал = ЭДС — ИК внутренний Сопротивление Закон Ома (I = V / R) резисторов последовательно I серия = I 1 = I 2 = I 3 Все резисторы в серии имеют одинаковый ток. V series = V 1 + V 2 + V 3 Падение напряжения между последовательно соединенными резисторами разделено в соответствии с сопротивлением — большее сопротивление, большее падение напряжения (V = IR). резисторы параллельно В параллельно = В 1 = В 2 = В 3 Все резисторы, включенные параллельно, имеют одинаковое напряжение. I параллельно = I 1 + I 2 + I 3 Ток между резисторами, включенными параллельно, делится в соответствии с сопротивлением — большее сопротивление, меньший ток (I = V / R). удельное сопротивление (ρ = RA / L) Удельное сопротивление обратно пропорционально проводимости. Большее удельное сопротивление, большее сопротивление материала. Преобразуя приведенное выше уравнение, чтобы получить R = ρL / A. Чтобы сделать провод с низким сопротивлением, выберите материал с низким удельным сопротивлением, пусть провод должен быть коротким и диаметр провода должен быть большим. Удлинители сделаны очень толстыми, чтобы снизить сопротивление, поэтому они не нагреваются и не вызывают возгорания. Емкость концепция конденсатора с параллельными пластинами C = Q / V = ​​εA / d Большая емкость создается за счет большего заряда пластин (Q) для данного напряжения (В), большей площади пластины (A) или меньшего расстояния между пластинами (d). V = Ed, где V — напряжение на конденсаторе, E — электрическое поле между конденсаторами, а d — расстояние между пластинами конденсатора. энергия заряженного конденсатора U = Q 2 / 2C = ½QΔV = ½C (ΔV) 2 U — потенциальная энергия заряженного конденсатора, Q — накопленный заряд (величина + Q или -Q на одна из пластин), C — емкость. конденсаторы последовательно 1 / C экв. = 1 / C 1 + 1 / C 2 + 1 / C 30 3 3 конденсаторы параллельно C экв = C 1 + C 2 + C 3 диэлектрик Диэлектрик = непроводящий материал. Вставка диэлектрика между пластинами конденсатора увеличивает емкость, увеличивая Q (если V постоянный) или уменьшая V (если Q постоянный). В = В 0 / κ C = κC 0 Разряд конденсатора через резистор Заряд Разряд Во время разряда конденсатора конденсатор действует как батарея и управляет током, который со временем уменьшается по мере разряда конденсатора. Теория проводимости На проводимость влияет концентрация электролита: Без электролита, без ионизации, без проводимости. Оптимальная концентрация электролита, наибольшая проводимость за счет наибольшей подвижности ионов. Слишком много электролита, слишком много ионов, меньшая подвижность ионов, меньшая проводимость. На проводимость влияет температура: В металлах проводимость уменьшается с повышением температуры. В полупроводниках проводимость увеличивается с увеличением температуры. При чрезвычайно низких температурах (ниже определенной критической температуры, как правило, на несколько градусов выше абсолютного нуля) некоторые материалы обладают сверхпроводимостью — практически нет сопротивления протеканию тока, в таких условиях ток будет замкнутым почти вечно. Электропроводность (σ) обратно пропорциональна удельному сопротивлению (ρ). Поместите конденсатор в раствор, раствор будет проводить ток между пластинами конденсатора, поэтому вы можете измерить проводимость раствора с помощью конденсатора. Цепи Мощность в цепях (P = VI, P = I 2 R) P = IV = I 2 R P — мощность, I — ток, V — напряжение, R — сопротивление. Энергетические компании стараются сэкономить количество меди, необходимой для линий электропередач, за счет использования более тонких проводов, что делает R довольно высоким. Чтобы минимизировать P, рассеиваемый проводами, они минимизируют I, увеличивая до максимума V. Вот почему линии электропередач передают электричество под высоким напряжением. Переменные токи и реактивные цепи Среднеквадратичный ток I rms = I max / √2 = 0,7 I max Среднеквадратичное напряжение В СКЗ = В макс / √2 = 0,7 В макс В СКЗ = I СКЗ R P среднекв. = I среднекв. В среднекв. = I 2 среднекв. R

Fsect4.PDF

% PDF-1.6 % 3 0 obj > эндобдж 105 0 объект [/ CalGray>] эндобдж 106 0 объект [/ CalRGB>] эндобдж 107 0 объект > поток application / pdf

Неизвестно

Fsect4.PDF

Среда, 29 июля 1998 г. 1:01:09 PMAcrobat PDFWriter 3.0 для Windows Microsoft Word 2012-06-12T12: 48: 12-04: 002012-06-12T12: 48: 12-04: 00uuid: 57a21a6c-d787-4a74-b8c2 -8c4e46d02a7auuid: 4b87336f-6f39-4491-86ec-995b34114f63 конечный поток эндобдж 108 0 объект > эндобдж 104 0 объект > эндобдж 5 0 obj > эндобдж 44 0 объект > эндобдж 65 0 объект > эндобдж 84 0 объект > эндобдж 83 0 объект > / Тип / Страница >> эндобдж 88 0 объект > / ProcSet 2 0 R >> / Тип / Страница >> эндобдж 91 0 объект > / ProcSet 2 0 R >> / Тип / Страница >> эндобдж 92 0 объект > поток ѐ`.q] р + 9

Как конденсатор работает от постоянного тока

В предыдущем посте мы рассмотрели концепцию, конструкцию и работу конденсатора как источника постоянного напряжения. Этот пост о Как конденсатор работает с DC . Конденсаторы широко используются в электронике постоянного тока. Когда мы думаем о постоянном токе и конденсаторе, возникают следующие вопросы:

.

1. Как конденсатор работает с входом постоянного тока?
2. Какое конечное напряжение конденсатора после зарядки?
3. Сколько времени требуется для зарядки / разрядки конденсатора?

Давайте обсудим решение вышеперечисленных вопросов.

Как конденсатор работает с постоянным током Конденсатор

выполняет три задачи в цепях постоянного тока, то есть принимает заряд, удерживает заряд и подает заряд в определенное время. Когда конденсатор подключен к источнику постоянного напряжения, конденсатор начинает процесс получения заряда. Это повысит напряжение на конденсаторе. Когда конденсатор набирает достаточный заряд, начинает течь ток, и вскоре напряжение на конденсаторе достигает значения, примерно равного напряжению источника постоянного тока. Когда на конденсаторе почти полное напряжение, через конденсатор больше не течет ток.Это займет некоторое время. Но есть интересный факт. Конденсатор не получит 100% заряда в тот же момент, когда на него будет подано постоянное напряжение. Конденсатор быстро получает первую часть от общего заряда, вторую часть медленно, третью часть медленнее и так далее. Следовательно, можно сказать, что конденсатор заряжается нелинейно.

Можно представить эту ситуацию на примере шины по аналогии с . Сравните автобус с конденсатором, свободное место с пространством и людей с электронами. В автобусе каждый старается занять место.Если остается меньше мест, людям нужно больше времени, чтобы найти свободное место. Точно так же электроны пытаются занять место на пластине конденсатора. Здесь электронам требуется время, чтобы попасть на пластины. Перемотайте конструкцию конденсатора. Для входного постоянного напряжения первая пластина заряжается до входного напряжения. Поскольку между двумя пластинами нет проводящего пути, второй пластине требуется некоторое время, чтобы зарядиться.

Это время определяет время зарядки конденсатора. Итак, нам необходимо выяснить параметры, от которых зависит время зарядки конденсатора.Согласно закону Ома, если сопротивление цепи увеличивается, меньше тока для зарядки конденсатора. Это увеличивает время, необходимое для зарядки конденсатора. Поскольку емкость и напряжение обратно пропорциональны друг другу, увеличение емкости требует больше времени для зарядки конденсатора. Таким образом, с помощью этих соотношений можно сказать, что время зарядки конденсатора зависит как от сопротивления цепи, так и от емкости конденсатора. Это постоянной времени конденсатора.Но процесс измерения времени зарядки конденсатора сложен, поскольку конденсатор никогда не будет заряжаться с одинаковой скоростью.

Время зарядки или постоянная времени обозначается как τ (тау). Он определяет время, необходимое конденсатору емкостью «C», последовательно включенным с сопротивлением «R» Ом, для получения первой части полного заряда. Постоянная времени может быть математически определена как

Время зарядки = сопротивление x емкость
τ = R x C

Постоянная времени — это время, необходимое конденсатору для увеличения напряжения или тока до 63.21% от максимума или уменьшение до 36,79% от начального значения.

Почему конденсатор заряжается до 63% приложенного напряжения?

Вот уравнение для напряжения на конденсаторе в любой момент времени во время зарядки.

В _c = В _i (1- e ^{-τ / RC} )

Где В _c = напряжение конденсатора, В _i = входное напряжение, t = время зарядки, R = сопротивление, C = емкость

Цепь зарядки конденсатора

E.грамм. для R = 10 МОм и C = 0,1 мкФ постоянная времени составляет 1 секунду. Это не означает, что конденсатор полностью зарядится за 1 секунду. Это означает, что конденсатор будет заряжен до 63% входного напряжения за 2 секунды. Если мы продолжим подавать напряжение, конденсатор займет 63% разницы между текущим напряжением и входным напряжением. Этот процесс будет повторяться до тех пор, пока конденсатор не зарядится полностью. Мы получаем значение 63% или 0,63, когда добавляем одну постоянную времени в уравнение выше. Мы можем рассчитать ток в конденсаторе в любой момент (время), используя закон Ома.Рассмотрим ту же схему, что обсуждалась ранее. Вот уравнение тока при зарядке конденсатора.

I _c = ^{( V _i — V _c )} ⁄ _R

В таблице ниже показаны значения напряжения и тока заряда конденсатора для соответствующей постоянной времени.

Положение переключателя	Постоянная времени (τ) (в секундах)	Напряжение зарядки конденсатора ( В c ) (в вольтах)	Ток зарядки конденсатора ( I c )
ВЫКЛ	0	0	10 мкА
НА	1RC	63.2120	3,6787 мкА
НА	2RC	86,4664	1,3533 мкА
НА	3RC	95.0212	0,4978 мкА
НА	4RC	98.1684	0,1831 мкА
НА	5RC	99.3262	0,0673 мкА
НА	8RC	99.9664	3,3546 нА
НА	11RC	99.9983	0,1670 нА
НА	14RC	99.9999	8,3152 pA
НА	17RC	99.9999	0,4139 pA

Термин 1RC, 2RC и т. Д. Определяет, сколько раз постоянное напряжение должно быть приложено к конденсатору. Таблица выше напоминает важный факт, связанный с конденсатором i.е. : конденсатор никогда не накопит полный заряд. . Каждый раз постоянное напряжение конденсатора медленно увеличивается (кроме первого), но никогда не будет равно входному напряжению. Ток, протекающий через цепь резисторного конденсатора, уменьшается с увеличением времени (τ). Вот график, показывающий поведение зарядного напряжения и тока конденсатора.

График зарядного тока и напряжения конденсатора

График напряжения и тока зарядки конденсатора экспоненциально растет и падает по своей природе соответственно.Кривая показывает, сколько времени нужно конденсатору для почти полного заряда. Экспоненциальный рост напряжения и экспоненциальный спад тока в емкостной цепи не одинаковы или не совпадают с фазой и . Обратите внимание, что ось x графика изменяется относительно значения на оси y, чтобы иметь четкое представление об изменении напряжения или тока. График не соответствует конкретному масштабу. Через 5RC секунд зарядный ток I _c ≈ 0 и напряжение зарядки V _c ≈ входное напряжение.

Разряд конденсатора в цепях постоянного тока

Есть несколько способов разрядить заряженный конденсатор. Самый простой способ — использовать светодиод или резистор последовательно с конденсатором. Мы должны проявлять особую осторожность при выборе резистора или светодиода для разряда конденсатора. Перед использованием рекомендуется указать такие характеристики, как мощность, значение в случае резистора и прямой ток, напряжение в случае светодиода. Схема разрядки конденсатора показана ниже.

Схема разряда конденсатора

Вот уравнения для напряжения на конденсаторе и тока в конденсаторе в любой момент времени во время разряда.

V _d = V _i ( e ^{-τ / RC} ) I _d = ^{V _d} ⁄ _{20 R}

В таблице ниже показаны значения напряжения и тока разряда конденсатора для соответствующей постоянной времени. Во время разряда напряжение, с которого конденсатор начинает разряжаться, составляет последний заряд

.

Положение переключателя	Постоянная времени (τ) (в секундах)	Напряжение зарядки конденсатора ( В d )	Ток зарядки конденсатора ( I d )
ВЫКЛ	0	≈ 100 В	10 мкА
НА	1RC	36.7879 В	3,6787 мкА
НА	2RC	13,5335 В	1,3533 мкА
НА	3RC	4,9877 В	0,4978 мкА
НА	4RC	1.8315 В	0,1831 мкА
НА	5RC	0,6737 В	0,0673 мкА
НА	8RC	0,0335 В	3.3546 нА
НА	11RC	1,6701 мВ	0,1670 нА
НА	14RC	30,5902 мкВ	8,3152 pA
НА	17RC	4,1399 мкВ	0,4139 pA

Во время разрядки напряжение и ток конденсатора быстро уменьшаются на 1RC-секунду, а после этого происходит медленное уменьшение обеих величин. Вот график напряжения и тока разряда конденсатора.Оба графика экспоненциально падают в природе. За 5RC секунд ток разряда I _d ≈ 0 и напряжение разряда В _d ≈ 0.

График тока и напряжения разряда конденсатора

Пока что это все. Надеюсь, теперь вы знаете, как конденсатор работает с постоянным током. В следующем посте мы узнаем о конденсаторах в цепях переменного тока. Спасибо, что прочитали, и не забудьте оставить комментарий.

Емкость

и емкостное реактивное сопротивление — Inst Tools

Конденсаторы

Изменение переменного напряжения, приложенного к конденсатору, заряда конденсатора и тока, протекающего через конденсатор, представлены на рисунке 3.

Рисунок 3: Напряжение, заряд и ток в конденсаторе

Ток, протекающий в цепи, содержащей емкость, зависит от скорости изменения напряжения. Текущий поток на Рисунке 3 наибольший в точках a, c и e. В этих точках напряжение изменяется с максимальной скоростью (т.е. проходит через ноль).

Между точками a и b напряжение и заряд увеличиваются, а ток проходит через конденсатор, но его значение уменьшается.В точке b конденсатор полностью заряжен, а ток равен нулю. От точек b до c напряжение и заряд уменьшаются по мере разряда конденсатора, и его ток течет в направлении, противоположном напряжению. От точек c до d конденсатор начинает заряжаться в противоположном направлении, а напряжение и ток снова в том же направлении.

В точке d конденсатор полностью заряжен, и ток снова равен нулю. От точек d до e конденсатор разряжается, и ток становится противоположным напряжению.На рисунке 3 показан ток, опережающий приложенное напряжение на 90 °. В любой чисто емкостной схеме на токоподводы подается напряжение под углом 90 °.

Емкостное реактивное сопротивление

Емкостное реактивное сопротивление — это сопротивление конденсатора или емкостной цепи протеканию тока. Ток, протекающий в емкостной цепи, прямо пропорционален емкости и скорости изменения приложенного напряжения. Скорость изменения приложенного напряжения определяется частотой источника питания; следовательно, если частота емкости данной цепи увеличивается, ток увеличивается.

Также можно сказать, что если частота или емкость увеличиваются, сопротивление току уменьшается; следовательно, емкостное реактивное сопротивление, которое противодействует протеканию тока, обратно пропорционально частоте и емкости.

Емкостное реактивное сопротивление X _C измеряется в омах, как и индуктивное реактивное сопротивление.

Уравнение ниже представляет собой математическое представление емкостного реактивного сопротивления.

где

f = частота (Гц)
π = ~ 3.14
C = емкость (фарады)

Уравнение ниже представляет собой математическое представление емкостного реактивного сопротивления, когда емкость выражается в микрофарадах (мкФ).

Уравнение ниже представляет собой математическое представление тока, протекающего в цепи с только емкостным реактивным сопротивлением.

, где
I = эффективный ток (A)
E = эффективное напряжение на емкостном реактивном сопротивлении (В)
X _C = емкостное реактивное сопротивление (Ом)

Пример:

Конденсатор 10 мкФ подключен к источнику питания 120 В, 60 Гц (см. Рисунок 4).Найдите емкостное реактивное сопротивление и ток, протекающий в цепи. Нарисуйте векторную диаграмму.

Рисунок 4: Схема и фазовая диаграмма

Решение:

1. Емкостное реактивное сопротивление

X _C = 1 000 000 / [(2) (3,14) (60) (10)]

X _C = 1000000/3768 = 265,4 Ом

2. Ток, протекающий в цепи

I = 120 / 265,4 = 0,452 ампер

3. На рисунке 4b изображена фазовая диаграмма, показывающая текущее опережающее напряжение под углом 90 °.

Молекулярные выражения: электричество и магнетизм

Введение в емкость

Емкость — это свойство электрического проводника, которое характеризует его способность накапливать электрический заряд. Электронное устройство, называемое конденсатором, предназначено для обеспечения емкости в электрической цепи, обеспечивая средства для хранения энергии в электрическом поле между двумя проводящими телами.

Примерно в 1745 году Эвальд Кристиан фон Клист и Питер ван Мушенбрук независимо друг от друга открыли емкость в электрической цепи.Занимаясь отдельными исследованиями электростатики, они обнаружили, что электрический заряд может сохраняться в течение определенного периода времени. Они использовали устройство, которое теперь называется лейденским сосудом, которое состояло из закрытого стеклянного сосуда, наполненного водой, с гвоздем, протыкающим пробку и погружающимся в воду. Они подключили гвоздь к электростатическому заряду. После отключения гвоздя от источника заряда они обнаружили, что при прикосновении к гвоздю можно почувствовать удар. Это продемонстрировало, что устройство накопило заряд.

В 1747 году Джон Бевис усовершенствовал устройство, заменив воду в кувшине металлической фольгой. Он выложил фольгу как внутри, так и снаружи банки. В результате получился конденсатор с двумя проводниками (внутренний и внешний слои металлической фольги), разделенные изоляционным стеклом на равных расстояниях. Эти конструктивные особенности заложены в современный конденсатор. Лейденская банка также использовалась Бенджамином Франклином для хранения заряда от молнии и в других экспериментах. Фактически, естественное явление молнии включает в себя емкость в том, что огромные электрические поля развиваются между слоями облаков или между облаками и землей до удара молнии.Мы создали учебник Java , который демонстрирует это явление.

	Интерактивное руководство по Java

Конденсаторы

используются во многих отношениях в электронных схемах, таких как барьеры для постоянного тока, хранение памяти в компьютерном чипе, хранение заряда для электронной фотовспышки или регулировка настроенной схемы, например, в радиоприемнике.

Описание конденсатора

Конденсатор в своей простейшей форме состоит из двух проводящих пластин, разделенных изолирующим слоем, называемым диэлектриком. Когда конденсатор подключен к цепи через источник напряжения, напряжение вынуждает электроны на поверхность одной пластины и отталкивает электроны от поверхности другой пластины, что приводит к разнице потенциалов между пластинами. Конденсаторы заряжаются и разряжаются по мере необходимости.Конденсаторы различаются размером и расположением пластин, а также типом используемых диэлектрических материалов. В зависимости от типа необходимого диэлектрика могут использоваться бумага, керамика, воздух, слюда и электролитические материалы. Емкость конденсатора может быть фиксированной или регулируемой (как в радиотюнере).

Зарядка конденсатора

Когда конденсатор подключен к источнику напряжения, например к батарее, напряжение заставляет электроны попадать на одну пластину, что приводит к отрицательно заряженной пластине.Электроны другой пластины отводятся аккумулятором, в результате чего пластина становится положительно заряженной. Поскольку диэлектрик между пластинами является изолятором, ток не может течь через него. Конденсатор имеет ограниченную емкость для хранения зарядов. Когда конденсатор достигает своей емкости, он полностью заряжается.

На следующих схемах показана зарядка конденсатора. На рисунке 2 показана схема, содержащая проводник, соединяющий батарею, разомкнутый переключатель и конденсатор.Конденсатор на Рисунке 2 не заряжен. Между пластинами нет разницы потенциалов.

Когда переключатель замкнут, как показано на рисунке 3, через проводник к пластинам конденсатора и от пластин конденсатора возникает мгновенный выброс тока. Когда ток достигает отрицательной пластины конденсатора, он останавливается диэлектриком.

Скачок электрического тока в конденсаторе вызывает противодействующую электродвижущую силу в проводнике и пластинах.Эта противодействующая электродвижущая сила называется реактивным сопротивлением. Когда реактивное сопротивление достигает уровня, равного напряжению батареи, конденсатор полностью заряжается. Дальнейшего протекания тока нет. Когда конденсатор полностью заряжен, переключатель может быть разомкнут, и конденсатор сохранит свой заряд (Рисунок 4). Из-за разницы зарядов на пластинах в конденсаторе есть источник потенциальной энергии. Запасенная энергия — это энергия, которая потребовалась для зарядки конденсатора.

Силовые линии между пластинами конденсатора представляют собой электрическое силовое поле (см. Рисунки 3 и 4).Это электрическое силовое поле существует из-за неравных зарядов, положительных и отрицательных, на внутренних поверхностях пластин. Ток не может проходить через электростатическое поле из-за диэлектрического изолятора. Другими словами, разность потенциалов между пластинами индуцирует внутри диэлектрика электростатическое поле, которое сохраняет заряд.

Разряд конденсатора

Заряженный конденсатор, показанный на рисунке 4, теперь является источником потенциальной энергии.Эта потенциальная энергия теперь доступна для предполагаемого электронного применения. Если переключатель замкнут, как показано на рисунке 5, ток немедленно начнет течь от отрицательной пластины к положительной пластине. Конденсатор разряжается.

Заряженный конденсатор является источником напряжения для протекания тока. Ток перестанет течь, когда заряды двух пластин снова станут равными, а это означает, что конденсатор полностью разряжен.

Мы смоделировали зарядку и разрядку конденсатора в нашем интерактивном руководстве по Java для конденсаторов .

	Интерактивное руководство по Java

Диэлектрические материалы

Диэлектрический материал в конденсаторе предотвращает прохождение тока между его пластинами. Он также служит средой для поддержки электростатической силы заряженного конденсатора.Для изготовления диэлектриков используются различные материалы, как показано в таблице ниже.

Диэлектрические материалы оцениваются на основе их способности выдерживать электростатические силы с точки зрения числа, называемого диэлектрической проницаемостью. Способность диэлектрика поддерживать электростатические силы прямо пропорциональна диэлектрической проницаемости. Вакуум — это стандарт, по которому оцениваются другие диэлектрики. Диэлектрическая проницаемость вакуума равна 1. Из диаграммы видно, что диэлектрическая проницаемость вакуума и воздуха очень мала.Поэтому воздух часто упоминается как имеющий диэлектрическую проницаемость 1,

.

Материал Диэлектрическая проницаемость Вакуум 1,0 Воздух 1.00059 Полистирол 2.5 Бумага 3,5 Слюда 5,4 Стеклянное стекло 9,9 Метиловый спирт 35 Глицерин 56,2 Чистая вода 81

Измерение емкости

Емкость измеряется в фарадах, он назван в честь Майкла Фарадея (1791-1867).Символ фарад — F. Если на пластины конденсатора помещен заряд в 1 кулон, а разность потенциалов между ними составляет 1 вольт, емкость определяется как 1 фарад. Один кулон равен заряду 6,25 х 10 ¹⁸ электронов. Один фарад — это очень большая емкость. Чаще используются микрофарады (10 ^-6 F) и пикофарады (10 ^-12 F).

Емкость конденсатора пропорциональна количеству заряда, который может храниться в нем для каждой разности потенциалов вольт между его пластинами.Математически это соотношение записывается как:

C = Q / V

Где C — емкость в фарадах, Q — количество накопленного электрического заряда в кулонах, а V — разность потенциалов в вольтах.

Следовательно, накопленный электрический заряд можно рассчитать по формуле:

Q = CV

Разность потенциалов или напряжений конденсатора можно рассчитать по формуле:

V = Q / C

Факторы, влияющие на значение емкости

На емкость конденсатора влияют три фактора:

1. Площадь тарелок
2. Расстояние между пластинами
3. Диэлектрическая проницаемость материала между пластинами

Пластины большего размера обеспечивают большую емкость для хранения электрического заряда.Следовательно, с увеличением площади пластин увеличивается емкость.

Емкость прямо пропорциональна электростатическому силовому полю между пластинами. Это поле тем сильнее, когда пластины расположены ближе друг к другу. Следовательно, с уменьшением расстояния между пластинами емкость увеличивается. По мере увеличения расстояния между пластинами емкость уменьшается.

Как обсуждалось выше, способность диэлектрика выдерживать электростатические силы прямо пропорциональна диэлектрической проницаемости.Следовательно, с увеличением диэлектрической проницаемости увеличивается емкость.

Принимая во внимание каждый из трех факторов, емкость конденсатора с двумя параллельными пластинами можно рассчитать по формуле:

C = (8,855 K A) ÷ д

Где C — емкость в пикофарадах, K — диэлектрическая проницаемость, A — площадь одной пластины в м ² , а d — расстояние между пластинами в м .

Наш Факторы, влияющие на емкость. Интерактивное руководство по Java демонстрирует изменения емкости при изменении размера пластин, расстояния и диэлектрической проницаемости.

	Интерактивное руководство по Java

Последовательные резистивно-емкостные цепи и постоянная времени

По мере того, как конденсатор заряжается, ток уменьшается, потому что напряжение, развиваемое конденсатором, увеличивается с течением времени и противодействует напряжению источника.Следовательно, скорость заряда конденсатора со временем снижается. Время, необходимое для зарядки и разрядки конденсатора, является очень важным фактором при проектировании электронных схем. Резисторы часто используются в сочетании с конденсаторами, чтобы контролировать время заряда и разряда, необходимое для предполагаемого применения. Сопротивление напрямую влияет на время, необходимое для зарядки конденсатора. По мере увеличения сопротивления для зарядки конденсатора требуется больше времени. Время, в течение которого конденсатор полностью заряжается в резистивно-емкостной (RC) цепи, зависит от номиналов конденсатора и резистора.

На следующем графике показана скорость заряда конденсатора в RC-цепи. Обратите внимание, что скорость заряда со временем значительно снижается. Вторая часть времени зарядки во много раз больше, чем первая. Фактически, конденсатор достигает 63,2% своего заряда за пятую часть времени, необходимого для полного заряда. Из-за этого конденсаторы в реальных приложениях обычно заряжаются не полностью. Конденсаторы в цепях обычно заряжены до 63,2% от полной емкости.Время, необходимое для зарядки конденсатора до 63,2% от его полной емкости, называется его постоянной времени RC (резистивно-емкостной).

Важно знать, как рассчитывать постоянные времени RC при проектировании различных типов электронных схем. Постоянную времени RC цепи можно рассчитать по следующей формуле:

т = C x R

Где t — время в секундах, C — емкость в фарадах, а R — сопротивление в омах.

Наш интерактивный учебник по Java RC с постоянной времени RC демонстрирует изменения постоянной времени RC при изменении значений сопротивления и емкости.

	Интерактивное руководство по Java

Конденсаторы в параллельных цепях

Емкость в цепи можно увеличить, подключив конденсаторы параллельно, как показано на следующей схеме:

Мы знаем, что емкость конденсатора можно увеличить, увеличив размер его пластин.При параллельном подключении двух или более конденсаторов размер пластины фактически увеличивается. Увеличение площади пластины позволяет хранить больше заряда и, следовательно, создавать большую емкость. Чтобы определить общую емкость нескольких параллельных конденсаторов, просто сложите их индивидуальные значения. Ниже приводится формула для расчета общей емкости в цепи, содержащей конденсаторы, включенные параллельно:

C _T = C ₁ + C ₂ + C ₃ .. .

Конденсаторы в последовательной цепи

Емкость в цепи может быть уменьшена путем последовательного включения конденсаторов, как показано на следующей диаграмме:

Мы знаем, что емкость конденсатора можно уменьшить, разместив пластины дальше друг от друга. Соединение двух или более конденсаторов последовательно увеличивает расстояние между пластинами и толщину диэлектрика, тем самым уменьшая величину емкости.

Ниже приводится формула для расчета общей емкости в цепи, содержащей два последовательно соединенных конденсатора:

C _T = (C ₁ x C ₂ x C ₃ ) _/ (C ₁ + C ₂ + C ₃ )

Номинальное напряжение конденсаторов

При выборе подходящего конденсатора для конкретного применения необходимо учитывать не только значение емкости, но и величину напряжения, которому будет подвергаться конденсатор.Конденсаторы рассчитаны на то, чтобы выдерживать определенное максимальное напряжение. Превышение максимального напряжения может привести к возникновению дуги через диэлектрик и повреждению конденсатора. Максимальное напряжение, которое может выдержать конденсатор, и есть его рабочее напряжение. Производитель указывает рабочее напряжение. Однако стандартная погрешность заключается в выборе конденсатора с рабочим напряжением, которое на 50 процентов выше максимального напряжения, которое будет использоваться в приложении.

Конденсаторы переменные

Есть два основных типа конденсаторов: постоянные и переменные.Конденсатор постоянной емкости имеет определенное значение емкости. Переменный конденсатор допускает диапазон емкости. Конденсаторы переменной емкости сконструированы таким образом, что емкость можно изменять с помощью механических средств, таких как регулировка винта или вращения вала. Переменные конденсаторы используются, когда приложение требует регулировки емкости, например, в радиотюнере.

Ниже представлен типичный конденсатор переменной емкости. Имеет два набора тарелок. Один набор называется ротором, а другой — статором.Ротор обычно подключается к ручке вне конденсатора. Два набора пластин расположены близко друг к другу, но не соприкасаются. Воздух является диэлектриком в конденсаторе переменной емкости. При повороте ручки наборы пластин становятся более или менее зацепленными, увеличивая или уменьшая расстояние между пластинами. По мере того, как пластины становятся более сетчатыми, емкость увеличивается. По мере того, как пластины становятся менее зацепленными, емкость уменьшается.

Наше интерактивное руководство по Java для переменного конденсатора демонстрирует механику переменного конденсатора.

	Интерактивное руководство по Java

Конденсаторы в действии

Компьютерная память

В большинстве случаев основная память компьютера — это высокоскоростная оперативная память (RAM). Возможны два типа основной памяти со схемами RAM, статическая память с произвольным доступом (SRAM) и динамическая память с произвольным доступом (DRAM).Одна микросхема памяти состоит из нескольких миллионов ячеек памяти. В микросхеме SRAM каждая ячейка памяти состоит из триггера схемы резистора для хранения двоичных цифр 1 или 0. В микросхеме DRAM каждая ячейка памяти состоит из конденсатора, а не триггера схемы резистора. Когда конденсатор электрически заряжен, говорят, что он хранит двоичную цифру 1, а когда он разряжен, он представляет 0. На рисунке 10 ниже показана часть микросхемы памяти, содержащая 16 ячеек памяти.

Конденсаторные микрофоны

Микрофон преобразует звуковые волны в электрический сигнал.Все микрофоны имеют диафрагму, которая вибрирует при ударе звуковых волн. Вибрирующая диафрагма, в свою очередь, заставляет электрический компонент создавать выходной ток с частотой, пропорциональной звуковым волнам. В конденсаторном микрофоне для этой цели используется конденсатор.

В конденсаторном микрофоне диафрагма — это отрицательно заряженная пластина заряженного конденсатора. Когда звуковая волна сжимает диафрагму, диафрагма перемещается ближе к положительной пластине. Уменьшение расстояния между пластинами увеличивает электростатическое притяжение между ними.Это приводит к протеканию тока к отрицательной пластине. По мере того как диафрагма выдвигается в ответ на звуковые волны, диафрагма перемещается дальше от положительной пластины. Увеличение расстояния между пластинами снижает электростатическое притяжение между ними. Это приводит к протеканию тока обратно к положительной пластине. Эти переменные потоки тока создают слабые электронные сигналы, которые поступают в смеситель, затем в усилитель и, наконец, в громкоговоритель. Вы можете понаблюдать за работой конденсаторного микрофона в нашем руководстве по Java для конденсаторного микрофона .

	Интерактивное руководство по Java

Радиоприемник

Конденсаторы переменной емкости используются в схемах настройки радиоприемников. На рисунке 11 переменный конденсатор подключен к цепи антенного трансформатора. Передаваемые радиоволны вызывают прохождение индуцированного тока в антенне через первичную катушку на землю.

Во вторичной обмотке индуцируется вторичный ток в противоположном направлении.Этот ток течет к конденсатору. Мы знаем, что скачок тока в конденсаторе вызывает противодействующую электродвижущую силу. Эта противодействующая электродвижущая сила называется реактивным сопротивлением. Индуцированный поток тока через катушку также вызывает противодействующую электродвижущую силу. Это называется индуктивным реактивным сопротивлением. Таким образом, у нас есть как емкостное, так и индуктивное реактивное сопротивление.

На более высоких частотах индуктивное реактивное сопротивление больше, а емкостное реактивное сопротивление меньше. На более низких частотах все наоборот.Переменный конденсатор используется для выравнивания индуктивного и емкостного реактивных сопротивлений. Состояние, при котором реактивные сопротивления уравновешены, называется резонансом. Конкретная частота, которая изолирована выровненными реактивными сопротивлениями, называется резонансной частотой.

Радиосхема настраивается путем регулирования емкости переменного конденсатора для выравнивания индуктивного и емкостного реактивного сопротивления цепи для желаемой резонансной частоты или, другими словами, для настройки на желаемую радиостанцию.Наш интерактивный учебник по Java для радиоприемника демонстрирует, как переменный конденсатор используется для настройки на радиочастоты.

	Интерактивное руководство по Java

Импульсные магниты

В Национальной лаборатории сильного магнитного поля магниты используются для исследований во всех областях науки, включая биологию, химию, геологию, инженерию, материаловедение и физику.Исследования в сильных магнитных полях имеют решающее значение, поскольку они позволяют ученым изучать материю на молекулярном уровне.

Один из используемых магнитов — это импульсный магнит. Импульсные магниты способны создавать магнитные поля до 800 тесла. Для создания таких сильных полей требуются чрезвычайно высокие электрические токи, часто в несколько десятков тысяч ампер. Импульсные магниты обычно питаются от конденсаторной батареи, устройства, содержащего большое количество конденсаторов, способных накапливать огромное количество электроэнергии.Конденсаторная батарея разряжается за доли секунды через катушку магнита. Типичная энергия составляет от 0,5 до 1 мегаджоулей. Мы смоделировали включение импульсного магнита в нашем интерактивном учебном пособии по Java для импульсного магнита .

	Интерактивное руководство по Java

---

Ссылки на дополнительную информацию об импульсных магнитах:

Что такое импульсный магнит?

---

НАЗАД НА ДОМ ЭЛЕКТРИЧЕСТВА И МАГНИТИЗМА

Вопросы или комментарии? Отправить нам письмо.

© 1995-2021, автор — Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения правообладателей.

No related posts.