Лабораторная работа №6
Краткие теоретические сведенияЭлектрический ток в
проводниках вызывают так называемые источники постоянного тока. Силы,
вызывающие перемещение электрических зарядов внутри источника
постоянного тока против направления действия сил электростатического
поля, называются сторонними силами. Отношение работы Астор.,
совершаемой сторонними силами по перемещению заряда D Q вдоль цепи, к
значению этого заряда называется электродвижущей силой e источника
(ЭДС):
(1) Электродвижущая сила выражается в тех же единицах, что и напряжение или разность потенциалов, т.е. в Вольтах.
Работа – эта мера превращения энергии из одного вида в другой. Следовательно, в источнике сторонняя энергия преобразуется в энергию электрического поля
W = e * Q
При движении заряда Q на внешнем участке цепи преобразуется энергия стационарного поля, созданного и поддерживаемого источником:
W1 = U * Q ,
(3)
а на внутреннем участке:
W2 = Uвн. * Q
(4)
* Q
(4)
По закону сохранения энергии
W = W1 + W2 или e * Q =
U * Q + Uвн. * Q (5)
Сократив на Q, получим:
e = Uвн. + U (6)
т.е. электродвижущая сила источника равна сумме напряжений на внешнем и внутреннем участке цепи.
При разомкнутой цепи Uвн.= 0, то
e = U (7)
Подставив в равенство (6) выражения для U и Uвн. по закону Ома для участка цепи
U = I * R; Uвн. = I * r,
получим:
e = I * R + I * r = I * (R + r) (8)
Отсюда
Тест итоговый по электротехнике
Тесты по электротехнике и электронике с ответами
1-вариант
1. Что такое электрический ток?
Что такое электрический ток?
A. графическое изображение элементов.
B. это устройство для измерения ЭДС.
C. упорядоченное движение заряженных частиц в проводнике.
D. беспорядочное движение частиц вещества.
E. совокупность устройств предназначенных для использования электрического сопротивления.
2. Устройство, состоящее из двух проводников любой формы, разделенных диэлектриком
A. электреты
B. источник
C. резисторы
D. реостаты
E. конденсатор
3. Закон Джоуля – Ленца
A. работа производимая источникам, равна произведению ЭДС источника на заряд, переносимый в цепи.
B. определяет зависимость между ЭДС источника питания, с внутренним сопротивлением.
C. пропорционален сопротивлению проводника в контуре алгебраической суммы.
D.
количество теплоты, выделяющейся в проводнике при прохождении по нему
электрического тока, равно произведению квадрата силы тока на сопротивление
проводника и время прохождения тока через проводник.
E. прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
4. Прибор
A. резистор
B. конденсатор
C. реостат
D. потенциометр
E. амперметр
5. Определите сопротивление нити электрической лампы мощностью 100 Вт, если лампа рассчитана на напряжение 220 В.
A. 570 Ом.
B. 488 Ом.
C. 523 Ом.
D. 446 Ом.
E. 625 Ом.
6. Физическая величина, характеризующую быстроту совершения работы.
A. работа
B. напряжения
C. мощность
D. сопротивления
E. нет правильного ответа.
7. Сила тока в электрической цепи 2 А при напряжении на его концах 5 В. Найдите сопротивление проводника.
A. 10 Ом
B. 0,4 Ом
C. 2,5 Ом
D. 4 Ом
E. 0,2 Ом
8. Закон Ома для полной цепи:
A. I= U/R
B. U=U*I
C. U=A/q
U=A/q
D. I===…=
E. I= E/ (R+r)
9. Диэлектрики, длительное время сохраняющие поляризацию после устранения внешнего электрического поля.
A. сегнетоэлектрики
B. электреты
C. потенциал
D. пьезоэлектрический эффект
E. электрический емкость
10. Вещества, почти не проводящие электрический ток.
A. диэлектрики
B. электреты
C. сегнетоэлектрики
D. пьезоэлектрический эффект
E. диод
11. Какие из перечисленных ниже частиц имеют наименьший отрицательный заряд?
A. электрон
B. протон
C. нейтрон
D. антиэлектрон
E. нейтральный
12. Участок цепи это…?
A. часть цепи между двумя узлами;
B. замкнутая часть цепи;
C. графическое изображение элементов;
D. часть цепи между двумя точками;
E.
элемент электрической цепи, предназначенный для использование
электрического сопротивления.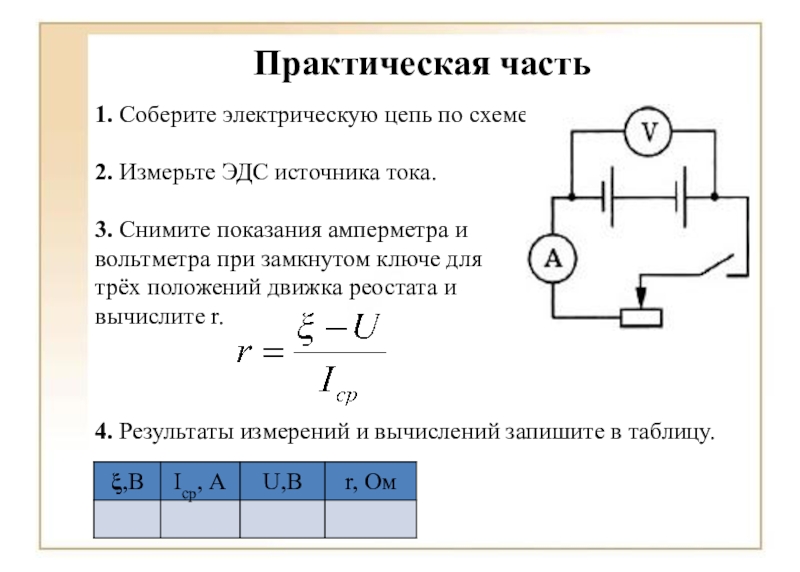
13. В приборе для выжигания по дереву напряжение понижается с 220 В до 11 В. В паспорте трансформатора указано: «Потребляемая мощность – 55 Вт, КПД – 0,8». Определите силу тока, протекающего через первичную и вторичную обмотки трансформатора.
A.
B.
C.
D.
E.
14. Преобразуют энергию топлива в электрическую энергию.
A. Атомные электростанции.
B. Тепловые электростанции
C. Механические электростанции
E. Ветроэлектростанции.
15. Реостат применяют для регулирования в цепи…
A. напряжения
B. силы тока
C. напряжения и силы тока
D. сопротивления
E. мощности
16. Устройство, состоящее из катушки и железного сердечника внутри ее.
A. трансформатор
B. батарея
C. аккумулятор
D. реостат
E. электромагнит
17. Диполь – это
A.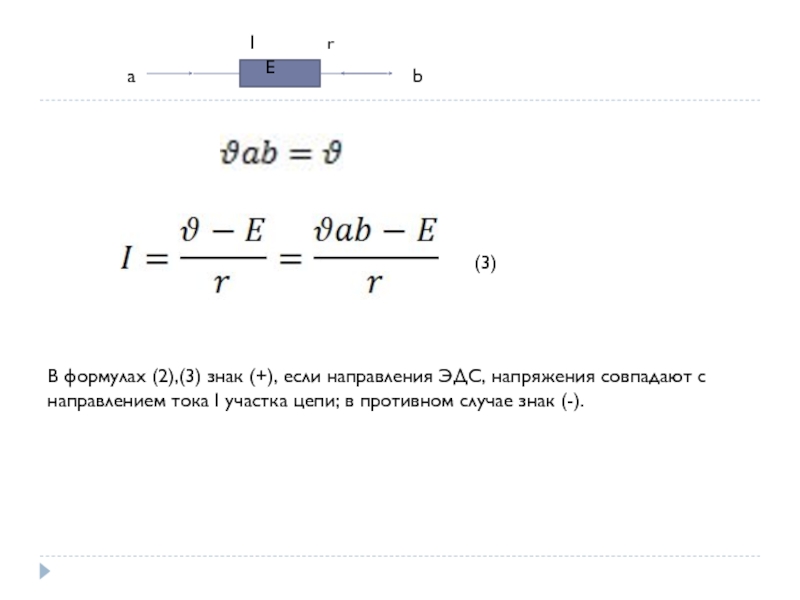 два разноименных электрических заряда, расположенных на небольшом
расстоянии друг от друга.
два разноименных электрических заряда, расположенных на небольшом
расстоянии друг от друга.
B. абсолютная диэлектрическая проницаемость вакуума.
C. величина, равная отношению заряда одной из обкладок конденсатора к напряжению между ними.
D. выстраивание диполей вдоль силовых линий электрического поля.
E. устройство, состоящее из двух проводников любой формы, разделенных диэлектриком.
18. Найдите неверное соотношение:
A. 1 Ом = 1 В / 1 А
B. 1 В = 1 Дж / 1 Кл
C. 1 Кл = 1 А * 1 с
D. 1 А = 1 Ом / 1 В
E. 1А = Дж/ с
19. При параллельном соединении конденсатор……=const
A. напряжение
B. заряд
C. ёмкость
D. сопротивление
E. силы тока
20. Вращающаяся часть электрогенератора.
A. статор
B. ротор
C. трансформатор
D. коммутатор
E. катушка
21. В
цепь с напряжением 250 В включили последовательно две лампы, рассчитанные на
это же напряжение. Одна лампа мощностью 500 Вт, а другая мощностью 25 Вт.
Определите сопротивление цепи.
Одна лампа мощностью 500 Вт, а другая мощностью 25 Вт.
Определите сопротивление цепи.
A. 2625 Ом.
B. 2045 Ом.
C. 260 Ом.
D. 238 Ом.
E. 450 Ом.
22. Трансформатор тока это…
A. трансформатор, предназначенный для преобразования импульсных сигналов с длительностью импульса до десятков микросекунд с минимальным искажением формы импульса.
B. трансформатор, питающийся от источника напряжения.
C. вариант трансформатора, предназначенный для преобразования электрической энергии в электрических сетях и в установках, предназначенных для приёма и использования электрической энергии.
D. трансформатор, питающийся от источника тока.
E. трансформатор, первичная обмотка которого электрически не связана со вторичными обмотками.
23. Какой величиной является магнитный поток Ф?
A. скалярной
B. векторной
C. механический
D. ответы А, В
E. перпендикулярный
24. Совокупность
витков, образующих электрическую цепь, в которой суммируются ЭДС, наведённые в
витках.
Совокупность
витков, образующих электрическую цепь, в которой суммируются ЭДС, наведённые в
витках.
A. магнитная система
B. плоская магнитная система
C. обмотка
D. изоляция
E. нет правильного ответа
25. Земля и проводящие слои атмосферы образует своеобразный конденсатор. Наблюдениями установлено, что напряженность электрического поля Земли вблизи ее поверхности в среднем равна 100 В/м. Найдите электрический заряд, считая, что он равномерно распределен по всей земной поверхности.
A. 4,2∙ Кл
B. 4,1∙ Кл
C. 4∙ Кл
D. 4,5∙ Кл
E. 4,6 ∙ Кл
2-вариант
1. Что такое электрическая цепь?
Что такое электрическая цепь?
A. это устройство для измерения ЭДС.
B. графическое изображение электрической цепи, показывающее порядок и характер соединение элементов.
C. упорядоченное движение заряженных частиц в проводнике.
D. совокупность устройств, предназначенных для прохождения электрического тока.
E. совокупность устройств предназначенных для использования электрического сопротивления.
2. ЭДС источника выражается формулой:
A. I= Q/t
B. E= Au/q
C. W=q*E*d
D.
E. U=A/q
3. Впервые явления в электрических цепях глубоко и тщательно изучил:
A. Майкл Фарадей
B. Джемс Максвелл
C. Георг Ом
D. Михаил Ломоносов
E. Шарль Кулон
4. Прибор
A. амперметр
B. реостат
C. резистор
D. ключ
E. потенциометр
5.
Ёмкость конденсатора С=10 мкФ, напряжение на обкладках U=220В. Определить заряд конденсатора.
Определить заряд конденсатора.
A. 2.2 Кл.
B. 2200 Кл.
C. 0,045 Кл.
D. 450 Кл.
E.
6. Это в простейшем случае реостаты, включаемые для регулирования напряжения.
A. потенциометры
B. резисторы
C. реостаты
D. ключ
E. счётчик
7. Часть цепи между двумя точками называется:
A. контур
B. участок цепи
C. ветвь
D. электрическая цепь
E. узел
8. Сопротивление последовательной цепи:
A.
B.
C.
D. .
E.
9. Сила тока в проводнике…
A. прямо пропорционально напряжению на концах проводника
B. прямо пропорционально напряжению на концах проводника и его сопротивлению
C. обратно пропорционально напряжению на концах проводника
D. обратно пропорционально напряжению на концах проводника и его сопротивлению
E. электрическим
зарядом и поперечное сечение проводника
электрическим
зарядом и поперечное сечение проводника
10. Какую энергию потребляет из сети электрическая лампа за 2 ч, если ее сопротивление 440 Ом, а напряжение сети 220 В?
A.
B. 240 Вт
C.
D. 375 Вт
E. 180 Вт
11. 1 гВт =
A. 1024 Вт
B. 1000000000 Вт
C. 1000000 Вт
D.
E. 100 Вт
12. Что такое потенциал точки?
A. это разность потенциалов двух точек электрического поля.
B. это абсолютная диэлектрическая проницаемость вакуума.
C. называют величину, равная отношению заряда одной из обкладок конденсатора к напряжению между ними.
D. называют устройство, состоящее из двух проводников любой формы, разделенных диэлектриком.
E. называют работу, по перемещению единичного заряда из точки поля в бесконечность.
13. Условное обозначение
A. резистор
B. предохранитель
C. реостат
D. кабель, провод,
шина электрической цепи
кабель, провод,
шина электрической цепи
E. приемник электрической энергии
14. Лампа накаливания с сопротивлением R= 440 Ом включена в сеть с напряжением U=110 В. Определить силу тока в лампе.
A. 25 А
B. 30 А
C. 12 А
D. 0,25 А
E. 1 А
15. Какие носители заряда существуют?
A. электроны
B. положительные ионы
C. отрицательные ионы
D. нейтральные
E. все перечисленные
16. Сколько в схеме узлов и ветвей?
A. узлов 4, ветвей 4;
B. узлов 2, ветвей 4;
C. узлов 3, ветвей 5;
D. узлов 3, ветвей 4;
E. узлов 3, ветвей 2.
17. Величина, обратная сопротивлению
A. проводимость
B. удельное сопротивление
C. период
D. напряжение
E. потенциал
18. Ёмкость конденсатора С=10 мФ; заряд конденсатора Q= 4∙ Определить напряжение на обкладках.
A. 0,4 В;
0,4 В;
B. 4 мВ;
C. 4∙ В;
D. 4∙ В;
E. 0,04 В.
19. Будет ли проходить в цепи постоянный ток, если вместо источника ЭДС – включить заряженный конденсатор?
A. не будет
B. будет, но недолго
C. будет
D. А, В
E. все ответы правильно
20. В цепи питания нагревательного прибора, включенного под напряжение 220 В, сила тока 5 А. Определить мощность прибора.
A. 25 Вт
B. 4,4 Вт
C. 2,1 кВт
D. 1,1 кВт
E. 44 Вт
21. Плотность электрического тока определяется по формуле:
A. …=q/t
B. …=I/S
C. …=dl/S
D. …=1/R
E. …=1/t
22. Определить количество теплоты, выделенное в нагревательном приборе в течение 0,5 ч, если он включен в сеть напряжением 110 В и имеет сопротивление 24 Ом.
A. 130 000 Дж
B. 650 000 Дж
C. 907 500 Дж
D. 235 кДж
E. 445 500 Дж
445 500 Дж
23. Магнитная система, в которой все стержни имеют одинаковую форму, конструкцию и размеры, а взаимное расположение любого стержня по отношению ко всем ярмам одинаково для всех стерней.
A. симметричная магнитная система
B. несимметричная магнитная система
C. плоская магнитная система
D. пространственная магнитная система
E. прямая магнитная система
24. Обеспечивает физическую защиту для активного компонента, а также представляет собой резервуар для масла.
A. обмотка
B. магнитная система
C. автотрансформатор
D. система охлаждения
E. бак
25. Трансформатор, предназначенный для преобразования импульсных сигналов с длительностью импульса до десятков микросекунд с минимальным искажением формы импульса.
A. трансформатор тока
B. трансформатор напряжение
C. автотрансформатор
D. импульсный трансформатор
E.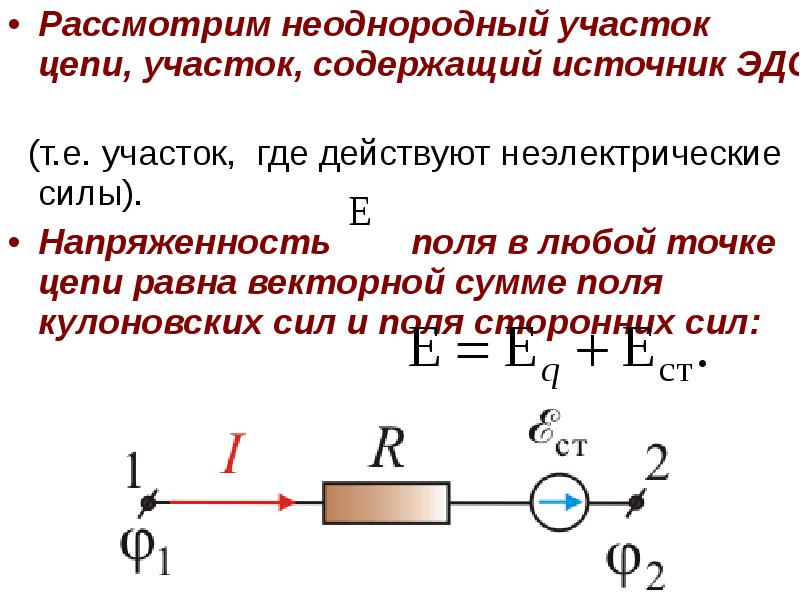 механический трансформатор.
механический трансформатор.
3-вариант
1. Что такое электрическое поле?
A. упорядоченное движение электрических зарядов.
B. особый вид материи, существующий вокруг любого электрического заряда.
C. упорядоченное движение заряженных частиц в проводнике.
D. беспорядочное движение частиц вещества.
E. взаимодействие электрических зарядов.
2. Внешняя часть цепи охватывает …
A. приемник соединительные провода
B. только источник питанья
только источник питанья
C. приемник
D. все элементы цепи
E. пускорегулирующую аппаратуру
3. Первый Закон Кирхгофа
A.
B.
C.
D.
E.
4. Прибор
A. реостат
B. резистор
C. батарея
D. потенциометр
E. ключ
5. Конденсатор имеет электроемкость С=5 пФ. Какой заряд находится на каждой из его обкладок, если разность потенциалов между ними U=1000 В?
A. 5,9∙ Кл
B. 5∙ Кл
C. 4,5∙ Кл
D. 4,7∙ Кл
E. 5,7∙ Кл
6. Какая величина равна отношению электрического заряда, прошедшего через поперечное сечение проводника, ко времени его прохождения?
A. сила тока
B. напряжение
C. сопротивление
D. работа тока
E. энергия
7. Единица измерения потенциала точки электрического поля…
A. Ватт
B. Ампер
C. Джоуль
Джоуль
D. Вольт
E. Ом
8. Определить мощность приёмника, если сопротивление равно 100 Ом, а ток приёмника 5 мА.
A. 500 Вт
B. 20 Вт
C. 0,5 Вт
D. 2500 Вт
E. 0,0025 Вт
9. Частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически совпадают.
A. вакуум
B. вода
C. плазма
D. магнитный поток
E. однозначного ответа нет
10. Какое из утверждений вы считаете не правильным?
A. Земной шар – большой магнит.
B. Невозможно получить магнит с одним полюсом.
C. Магнит имеет две полюса: северный и южный, они различны по своим свойствам.
D. Магнит – направленное движение заряженных частиц.
E. Магнит, подвешенный на нити, располагается определенным образом в пространстве, указывая север и юг.
11. В 1820 г. Кто экспериментально обнаружил, что электрический ток связан с магнитным полем?
A.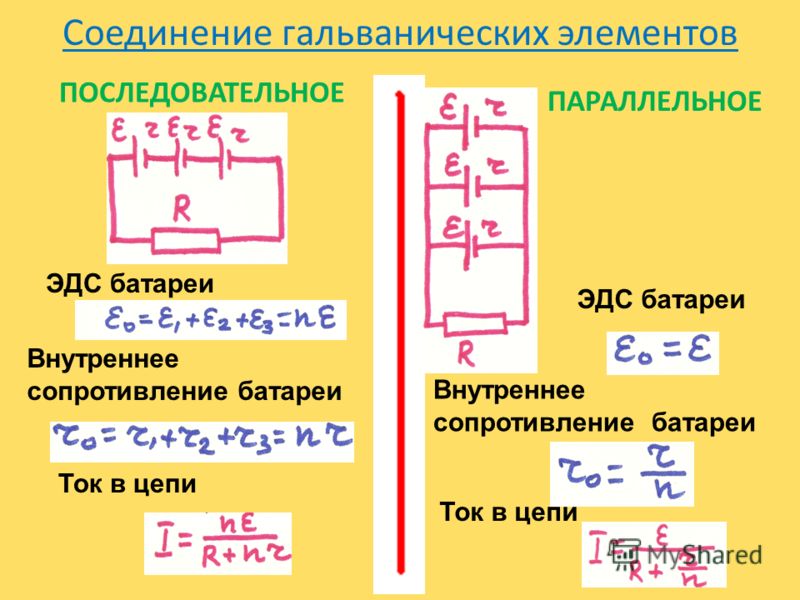 Майкл Фарадей
Майкл Фарадей
B. Ампер Андре
C. Максвелл Джеймс
D. Эрстед Ханс
E. Кулон Шарль
12. Ёмкость конденсатора С=10 мФ; заряд конденсатора Q= 4∙ Определить напряжение на обкладках.
A. 0,4 В;
B. 4 мВ;
C. 4∙ В;
D. 4∙ В;
E. 0,04 В.
13. К магнитным материалам относятся
A. алюминий
B. железо
C. медь
D. кремний
E. все ответы правильно
14. Диэлектрики применяют для изготовления
A. магнитопроводов
B. обмоток катушек индуктивности
C. корпусов бытовых приборов
D. корпусов штепсельных вилок
E. А, В.
15. К полупроводниковым материалам относятся:
A. алюминий
B. кремний
C. железо
D. нихром
E. В, D.
16. Единицами измерения магнитной индукции являются
A. Амперы
B. Вольты
C. Теслы
D. Герцы
Герцы
E. Фаза
17. Величина индуцированной ЭДС зависит от…
A. силы тока
B. напряжения
C. скорости вращения витка в магнитном поле
D. длины проводника и силы магнитного поля
E. ответы 1, 2
18. Выберите правильное утверждение:
A. ток в замкнутой цепи прямо пропорционален электродвижущей силе и обратно пропорционален сопротивлению всей цепи.
B. ток в замкнутой цепи прямо пропорционален сопротивлению всей цепи и обратно пропорционален электродвижущей силе.
C. сопротивление в замкнутой цепи прямо пропорционально току всей цепи и обратно пропорционально электродвижущей силе.
D. электродвижущая сила в замкнутой цепи прямо пропорциональна сопротивлению всей цепи и обратно пропорциональна току.
E. электродвижущая сила в замкнутой цепи прямо пропорциональна.
19. Если неоновая лампа мощностью 4,8 Вт рассчитана на напряжение 120 В, то потребляемый ток составляет:
A. 576 А
576 А
B. 115,2 А
C. 124,8 А
D. 0,04 А
E. 54 A
20. Формула Мощность приёмника:
A. N=EI
B. N=U/I
C. N=U/t
D. P=A*t
E. P=U*q/t
21. При параллельном соединении конденсатор ……=const
A. напряжение
B. заряд
C. ёмкость
D. индуктивность
E. А, В.
22. Конденсатор имеет две пластины. Площадь каждой пластины составляет 15 . Между пластинками помещен диэлектрик – пропарафинированная бумага толщиной 0,02 см. Вычислить емкость этого конденсатора. (e=2,2)
A. 1555 пФ
B. 1222 пФ
C. 1650 пФ
D. 550 пФ
E. 650 пФ
23. Что такое Пик — трансформатор
A. трансформатор, предназначенный для преобразования импульсных сигналов с длительностью импульса до десятков микросекунд с минимальным искажением формы импульса
B. трансформатор,
питающийся от источника напряжения.
C. вариант трансформатора, предназначенный для преобразования электрической энергии в электрических сетях и в установках, предназначенных для приёма и использования электрической энергии.
D. трансформатор, питающийся от источника тока.
E. трансформатор, преобразующий напряжение синусоидальной формы в импульсное напряжение с изменяющейся через каждые полпериода полярностью.
24. Определить мощность приёмника, если сопротивление равно 110 Ом, а ток приёмника 5 мА.
A. 0,0025 Вт
B. 0,00275 Вт
C. 20 Вт
D. 0,5 Вт
E. 2500 Вт
25. Разделительный трансформатор это…
A. трансформатор, предназначенный для преобразования импульсных сигналов с длительностью импульса до десятков микросекунд с минимальным искажением формы импульса.
B. трансформатор, предназначенный
для преобразования импульсных сигналов с длительностью импульса до десятков
микросекунд с минимальным искажением формы импульса.
C. трансформатор, питающийся от источника тока.
D. трансформатор, первичная обмотка которого электрически не связана со вторичными обмотками.
E. трансформатор, питающийся от источника напряжения.
4-вариант
1. Электрический ток в металлах — это…
A. беспорядочное движение заряженных частиц
B.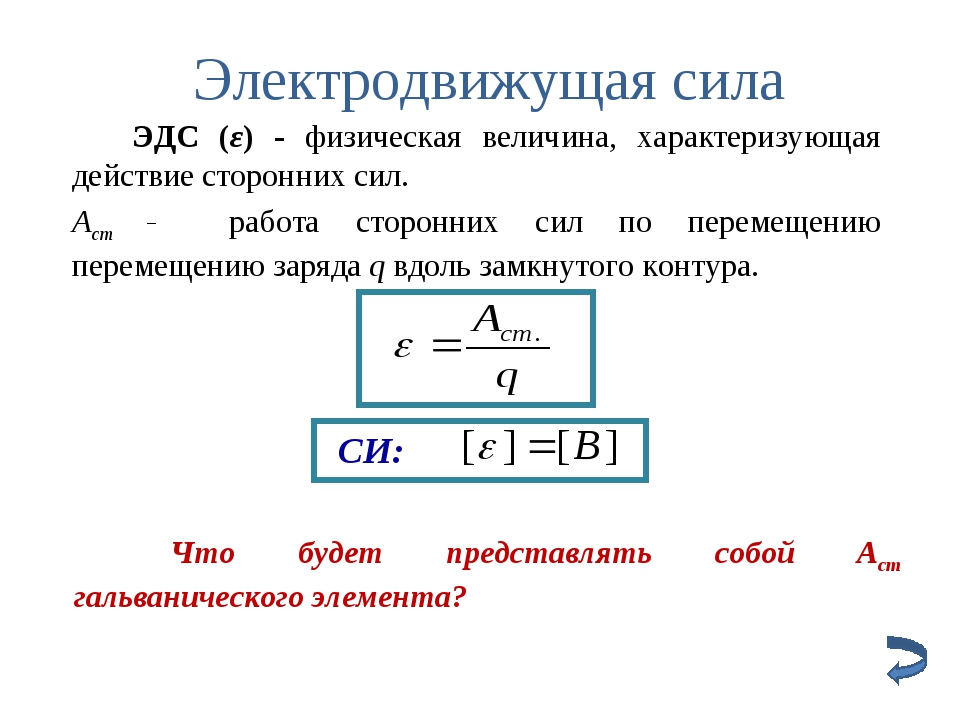 движение атомов и молекул.
движение атомов и молекул.
C. движение электронов.
D. направленное движение свободных электронов.
E. движение ионов.
2. Что такое резистор?
A. графическое изображение электрической цепи показывающие порядок и характер соединений элементов;
B. совокупность устройств предназначенного для прохождение электрического тока обязательными элементами;
C. порядочное движение заряженных частиц, замкнутом контуре, под действием электрического поля;
D. элемент электрической цепи, предназначенный для использования его электрического сопротивления;
E. работа, совершаемая единицу времени или величина, численно равняя скорости преобразования энергий.
3. Электрический ток оказывает на проводник действие…
A. тепловое
B. радиоактивное
C. магнитное
D. физическое
E. все ответы правильны
4.
Сопротивление тела человека электрическому току зависит от. ..
..
A. роста человека
B. массы человека
C. силы тока
D. физического состояния человека
E. не зависть
5. Прибор
A. гальванометр
B. ваттметр
C. источник
D. резистор
E. батарея
6. Закон Ома выражается формулой
A. U = R/I
B. U = I/R
C. I = U/R
D. R=I/U
E. I= E/ (R+r)
7. Определить количество теплоты, выделенное в нагревательном приборе в течение 0,5 ч, если он включен в сеть напряжением 110 В и имеет сопротивление 24 Ом.
A. 350 000 Дж
B. 245 550 Дж
C. 907 500 Дж
D. 45 кДж
E. 330 000 Дж
8. При последовательном соединении конденсатов …..=const
A. напряжение
B. заряд
C. ёмкость
D. индуктивность
E. А, В.
9.
Расстояние между пластинами плоского конденсатора увеличили в два раза. Электрическая ёмкость его…
Электрическая ёмкость его…
A. уменьшиться
B. увеличится
C. не изменится
D. недостаточно данных
E. уменьшиться и увеличиться
10. Ёмкость конденсатора С=10 мФ; заряд конденсатора q=4* Кл. Определить напряжение на обкладках.
A. 0,4 В;
B. 4 мВ;
C. 4∙ В;
D. 4∙ В;
E. 0,04 В.
11. За 2 ч при постоянном токе был перенесён заряд в 180 Кл. Определите силу тока.
A. 180 А
B. 90 А
C. 360 А
D. 0,025 А
E. 1 А
12. Элемент электрической цепи, предназначенный для использования его электрического сопротивления называется
A. клеммы
B. ключ
C. участок цепи
D. резистор
E. реостат
13. Внешняя часть цепи охватывает …
A. приемник
B. соединительные провода
C. только источник питания
D. пускорегулирующую аппаратуру
E. все элементы цепи
14. Сила
индукционного тока зависит от чего?
Сила
индукционного тока зависит от чего?
A. от скорости изменения магнитного поля
B. от скорости вращение катушки
C. от электромагнитного поля
D. от числа ее витков
E. А, D.
15. Алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжения на всех элементах данного контура:
A. первый закон Ньютона
B. первый закон Кирхгофа
C. второй закон Кирхгофа
D. закон Ома
E. С, Д.
16. Наименьшая сила тока, смертельно опасная для человека равна…
A. 1 А
B. 0,01 А
C. 0,1 А
D. 0,025 А
E. 0,2 А
17. Диэлектрики, обладающие очень большой диэлектрической проницаемостью
A. электреты
B. пьезоэлектрический эффект
C. электрон
D. потенциал
E. сегнетоэлектрики
18. К батареи, ЭДС которой 4,8 В и внутреннее сопротивление 3,5
Ом, присоединена электрическая лампочка сопротивлением 12,5 Ом. Определите ток
батареи.
Определите ток
батареи.
A. 0,5 А
B. 0,8 А
C. 0,3 А
D. 1 А
E. 7 А
19. Магнитные материалы применяют для изготовления
A. радиотехнических элементов
B. экранирования проводов
C. обмоток электрических машин
D. якорей электрических машин
E. A, B
20. Определите коэффициент мощности двигателя, полное сопротивление обмоток которого 20 Ом, а активное сопротивление 19 Ом.
A. 0,95
B. 0,45
C. 380
D. 1,9
E. 39
21. Кто ввел термин «электрон» и рассчитал его заряд?
A. А. Беккерель
B. Э. Резерфорд
C. Н. Бор
D. Д. Стоней
E. М. Планк
22. Если неоновая лампа мощностью 4,8 Вт рассчитана на напряжение 120 В, то потребляемый ток составляет:
A. 124,8 А
B. 115,2 А
C. 0,04 А
D. 0,5 А
E. 25 A
23. Условное обозначение
A.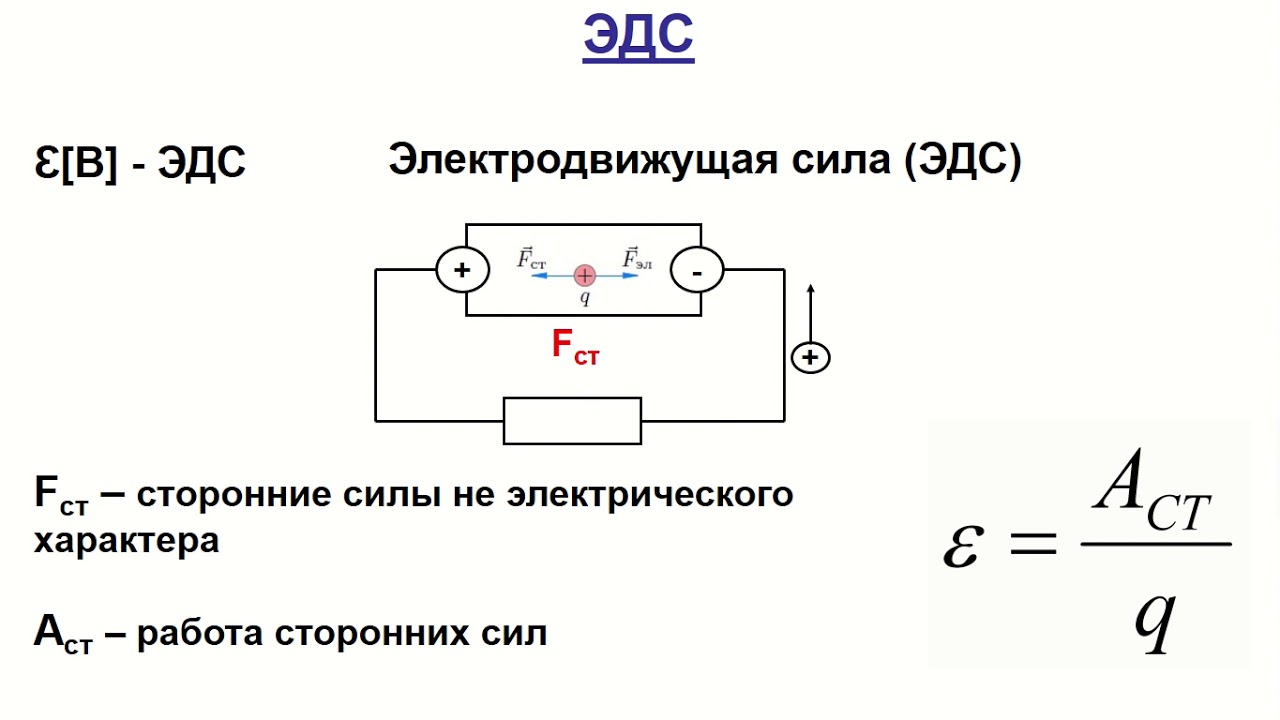 Амперметр
Амперметр
B. Вольтметр
C. Гальванометр
D. Клеммы
E. Генератор
24. Силовой трансформатор это…
A. трансформатор, предназначенный для преобразования импульсных сигналов с длительностью импульса до десятков микросекунд с минимальным искажением формы импульса.
B. вариант трансформатора, предназначенный для преобразования электрической энергии в электрических сетях и в установках, предназначенных для приёма и использования электрической энергии.
C. трансформатор, питающийся от источника напряжения.
D. трансформатор, питающийся от источника тока.
E. вариант трансформатора, предназначенный для преобразования электрической энергии в электрических сетях и в установках, предназначенных для приёма и использования электрической энергии.
25. В замкнутой цепи течет ток 1 А. внешнее сопротивление цепи 2 Ом. Определите внутреннее сопротивление источника, ЭДС которого составляет 2,1 В.
A.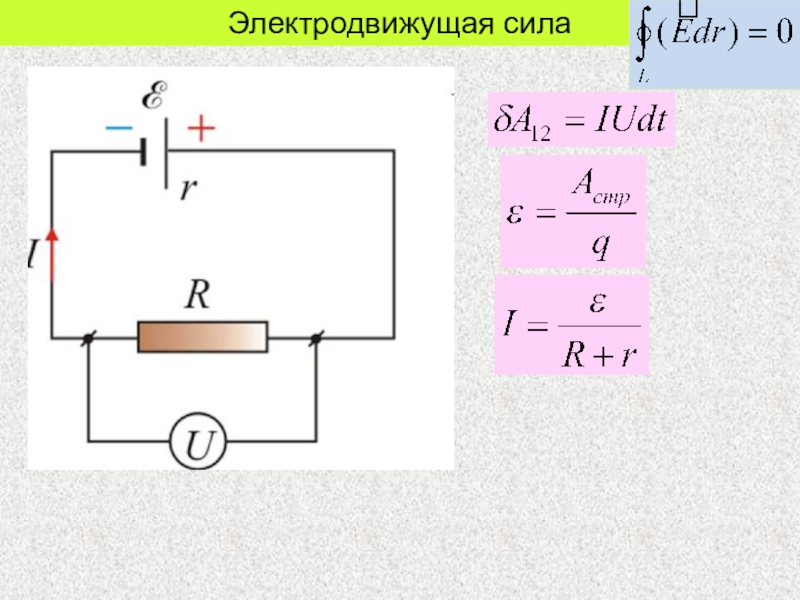 120 Ом
120 Ом
B. 0,1 Ом
C. 50 Ом
D. 1,05 Ом
E. 4,1 Ом
1-вариант | 2-вариант | 3-вариант | 4-вариант |
1. С | 1. D | 1.В | 1.D |
2. Е | 2.В | 2.D | 2. |
3. D | 3.С | 3.D | 3.C,А |
4. А | 4.D | 4.В | 4.С |
5. В | 5.Е | 5.В | 5.Е |
6. С | 6.А | 6.A | 6.C |
7. С | 7.В | 7.D | 7.С |
8. Е | 8.D | 8.Е | 8.B |
9. В | 9. | 9.С | 9.А |
10. А | 10.С | 10.D | 10.В |
11. А | 11.Е | 11.D | 11.Е |
12. D | 12.Е | 12.B | 12.D |
13. D | 13.В | 13.С | 13.E |
14. В | 14.D | 14.D | 14.E |
15. С | 15. | 15.B | 15.C |
16. Е | 16.А | 16.С | 16.А |
17. А | 17.А | 17.D | 17.Е |
18. D | 18.В | 18.A | 18.С |
19. А | 19.В | 19.D | 19.D |
20. В | 20.D | 20.E | 20.А |
21. А | 21. | 21.А | 21.D |
22. D | 22.С | 22.С | 22.C |
23. В | 23.А | 23.Е | 23.С |
24. С | 24.Е | 24.В | 24.Е |
25. D | 25.D | 25.D | 25.В |
Внутреннее сопротивление источника тока. Сопротивление
Лабораторная работа
«Измерение ЭДС и внутреннего сопротивления источника тока»
Дисциплина Физика
Преподаватель Виноградов А. Б.
Б.
Нижний Новгород
2014 г.
Цель работы: сформировать умение определения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.
Оборудование: выпрямитель ВУ-4М, амперметр, вольтметр, соединительные провода, элементы планшета №1: ключ, резистор R 1 .
Теоретическое содержание работы .
Внутреннее сопротивление источника тока.
При прохождении тока по замкнутой цепи, электрически заряженные частицы перемещаются не только внутри проводников, соединяющих полюса источника тока, но и внутри самого источника тока. Поэтому в замкнутой электрической цепи различают внешний и внутренний участки цепи. Внешний участок цепи составляет вся та совокупность проводников, которая подсоединяется к полюсам источника тока. Внутренний участок цепи — это сам источник тока. Источник тока, как и любой другой проводник, обладает сопротивлением. Таким образом, в электрической цепи, состоящей из источника тока и проводников с электрическим сопротивлением R , электрический ток совершает работу не только на внешнем, но и на внутреннем участке цепи. Например, при подключении лампы накаливания к гальванической батарее карманного фонаря электрическим током нагреваются не только спираль лампы и подводящие провода, но и сама батарея. Электрическое сопротивление источника тока называется внутренним сопротивлением. В электромагнитном генераторе внутренним сопротивлением является электрическое сопротивление провода обмотки генератора. На внутреннем участке электрической цепи выделяется количество теплоты, равное
Таким образом, в электрической цепи, состоящей из источника тока и проводников с электрическим сопротивлением R , электрический ток совершает работу не только на внешнем, но и на внутреннем участке цепи. Например, при подключении лампы накаливания к гальванической батарее карманного фонаря электрическим током нагреваются не только спираль лампы и подводящие провода, но и сама батарея. Электрическое сопротивление источника тока называется внутренним сопротивлением. В электромагнитном генераторе внутренним сопротивлением является электрическое сопротивление провода обмотки генератора. На внутреннем участке электрической цепи выделяется количество теплоты, равное
где r — внутреннее сопротивление источника тока.
Полное количество теплоты, выделяющееся при протекании постоянного тока в замкнутой цепи, внешний и внутренний участки которой имеют сопротивления, соответственно равные R и r , равно
. (2)
Всякую замкнутую цепь можно представить как два последовательно соединенных резистора с эквивалентными сопротивлениями R и r . Поэтому сопротивление полной цепи равно сумме внешнего и внутреннего сопротивлений:
Поэтому сопротивление полной цепи равно сумме внешнего и внутреннего сопротивлений:
. Поскольку при последовательном соединении сила тока на всех участках цепи одинакова, то через внешний и внутренний участок цепи проходит одинаковый по величине ток. Тогда по закону Ома для участка цепи падение напряжений на ее внешнем и внутреннем участках будут соответственно равны:
и
(3)
Электродвижущая сила.
Полная работа сил электростатического поля при движении зарядов по замкнутой цепи постоянного тока равна нулю. Следовательно, вся работа электрического тока в замкнутой электрической цепи оказывается совершенной за счет действия сторонних сил, вызывающих разделение зарядов внутри источника и поддерживающих постоянное напряжение на выходе источника тока. Отношение работы
, совершаемой сторонними силами по перемещению заряда q вдоль цепи, к значению этого заряда называется электродвижущей силой источника (ЭДС) :
, (4)
где
— переносимый заряд.
ЭДС выражается в тех же единицах, что и напряжение или разность потенциалов, т. е. в вольтах:
.
Закон Ома для полной цепи.
Если в результате прохождения постоянного тока в замкнутой электрической цепи происходит только нагревание проводников, то по закону сохранения энергии полная работа электрического тока в замкнутой цепи, равная работе сторонних сил источника тока, равна количеству теплоты, выделившейся на внешнем и внутреннем участках цепи:
. (5)
Из выражений (2), (4) и (5) получаем:
. (6)
Так как
, то
, (7)
или
. (8)
Сила тока в электрической цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна сумме электрических сопротивлений внешнего и внутреннего участков цепи. Выражение (8) называется законом Ома для полной цепи.
Таким образом, с точки зрения физики Закон Ома выражает закон сохранения энергии для замкнутой цепи постоянного тока.
Порядок выполнения работы .
Подготовка к выполнению работы.
Перед вами на столах находится минилаборатория по электродинамике. Её вид представлен в л. р. № 9 на рисунке 2.
Слева находятся миллиамперметр, выпрямитель ВУ-4М, вольтметр, амперметр. Справа закреплен планшет № 1 (см. рис. 3 в л. р. № 9). В задней секции корпуса размещаются соединительные провода цветные: красный провод используют для подключения ВУ-4М к гнезду «+» планшета; белый провод — для подключения ВУ-4М к гнезду «-»; желтые провода — для подключения к элементам планшета измерительных приборов; синие — для соединения между собой элементов планшета. Секция закрыта откидной площадкой. В рабочем положении площадка располагается горизонтально и используется в качестве рабочей поверхности при сборке экспериментальных установок в опытах.
2. Ход работы.
В ходе работы вы освоите метод измерения основных характеристик источника тока, используя закон Ома для полной цепи, который связывает силу тока I в цепи, ЭДС источника тока , его внутреннее сопротивление r и сопротивление внешней цепи R соотношением:
. (9)
1 способ.
Схема экспериментальной установки показана на рисунке 1.
Рис.1.
Внимательно изучите её. При разомкнутом ключе В источник замкнут на вольтметр, сопротивление которого много больше внутреннего сопротивления источника (r R ). В этом случае ток в цепи настолько мал, что можно пренебречь значением падения напряжения на внутреннем сопротивлении источника
, и ЭДС источника с пренебрежимо малой погрешностью равна напряжения на его зажимах , которое измеряется вольтметром, т.е.
. (10)
Таким образом, ЭДС источника определяется по показаниям вольтметра при разомкнутом ключе В.
Если ключ В замкнуть, вольтметр покажет падение напряжения на резисторе R :
. (11)
Тогда на основании равенств (9), (10) и (11) можно утверждать, что
(12)
Из формулы (12) видно, что для определения внутреннего сопротивления источника тока необходимо, кроме его ЭДС, знать силу тока в цепи и напряжение на резисторе R при замкнутом ключе.
Силу тока в цепи можно измерить при помощи амперметра. Проволочный резистор изготовлен из нихромовой проволоки и имеет сопротивление 5 Ом.
Соберите цепь по схеме, показанной на рисунке 3.
После того, как цепь будет собрана, необходимо поднять руку, позвать учителя, чтобы он проверил правильность сборки электрической цепи. И если цепь собрана правильно, то приступайте к выполнению работы.
При разомкнутом ключе В снимите показания вольтметра и занесите значение напряжения в таблицу 1. Затем замкните ключ В и опять снимите показания вольтметра, но уже и показания амперметра. Занесите значение напряжения и силы тока в таблицу 1.
Вычислите внутреннее сопротивление источника тока.
Таблица1.
, В
, В
I , А
, В
r , Ом
2 способ.
Сначала соберите экспериментальную установку, изображенную на рисунке 2.
Рис. 2.
Измерьте силу тока в цепи при помощи амперметра, результат запишите в тетрадь. Сопротивление резистора =5 Ом. Все данные заносятся в таблицу 2. , Ом
Контрольные вопросы :
Внешний и внутренний участки цепи.
Какое сопротивление называются внутренним? Обозначение.
Чему равно полное сопротивление?
Дайте определение электродвижущей силы (ЭДС). Обозначение. Единицы измерения.
Сформулируйте закон Ома для полной цепи.
Если бы мы не знали значения сопротивлений проволочных резисторов, то можно ли было бы использовать второй способ и что для этого надо сделать (может нужно, например, включить в цепь какой-нибудь прибор)?
Уметь собирать электрические цепи, используемые в работе.
Литература
Кабардин О. Ф.. Справ. Материалы: Учеб. Пособие для учащихся.-3-е изд.-М.:Просвещение,1991.-с.:150-151.
Справочник школьника. Физика/ Сост. Т. Фещенко, В. Вожегова.–М.: Филологическое об-щество «СЛОВО», ООО «Фирма» «Издательство АСТ», Центр гуманитарных наук при ф-те журна-листики МГУ им. М. В. Ломоносова, 1998. — с.: 124,500-501.
Самойленко П. И.. Физика (для нетехнических специальностей): Учебн. для общеобразоват. учреждений сред. Проф. Образования/ П. И.Самойленко, А. В. Сергеев.-2-е изд., стер.-М.: Издательский центр «Академия», 2003-с.: 181-182.
Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.
Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.
Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.
К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредственно к выходным гнездам источника подключают еще и вольтметр.
ЭДС измеряют по показанию вольтметра при разомкнутом ключе. Этот прием определения ЭДС основан на следствии из закона Ома для полной цепи, согласно которому при бесконечно большом сопротивлении внешней цепи напряжение на зажимах источника равно его ЭДС. (См. параграф «Закон Ома для полной цепи» учебника «Физика 10»).
Для определения внутреннего сопротивления источника замыкают ключ К. При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока). Поскольку ЭДС источника равна сумме падения напряжений на внутреннем и внешнем участках цепи:
ε = U r +U R , то U r = ε -U R (1)
По закону Ома для участка цепи U r = I· r (2). Подставив равенство (2) в (1) получают:
I · r = ε — U r , откуда r = (ε — U R )/ J
Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо предварительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внешнем сопротивлении, а также силу тока в нем.
Ход работы
1. Подготовьте таблицу для записи результатов измерений и вычислений:
ε ,в | U r , B | i,a | r , Ом |
Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.
После проверки схемы соберите электрическую цепь. Ключ разомкните.
Измерьте величину ЭДС источника.
Замкните ключ и определите показания амперметра и вольтметра.
Вычислите внутреннее сопротивление источника.
Определение эдс и внутреннего сопротивления источника тока графическим методом
Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замыкания источника тока, основанный на анализе графика зависимости напряжения на выходе источника от силы тока в цепи.
Оборудование: гальванический элемент, амперметр, вольтметр, резистор R 1 , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.
Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:
так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).
Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I К.З. — силу тока короткого замыкания (ток, который потечет в цепи источника, когда внешнее сопротивление R станет равным нулю).
ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика соответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.
Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.
Внутреннее сопротивление источника находят по тангенсу угла наклона графика относительно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомните смысл коэффициента при X).
Ход работы
- После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источнику тока, будет максимальным.
Для записи результатов измерений подготовьте таблицу:
Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.
Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.
Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по вертикальной оси, а силу тока — по горизонтальной. Проведите по точкам прямую линию.
Продолжите график до пересечения с осями координат и определите величины Е и, I К.З.
Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней цепи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.
Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла наклона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е / I К.З
Мы пришли к выводу, что для поддержания постоянного тока в замкнутой цепи, в нее необходимо включить источник тока. Подчеркнем, что задача источника заключается не в том, чтобы поставлять заряды в электрическую цепь (в проводниках этих зарядов достаточно), а в том, чтобы заставлять их двигаться, совершать работу по перемещению зарядов против сил электрического поля. Основной характеристики источника является электродвижущая сила 1 (ЭДС) − работа, совершаемая сторонними силами по перемещению единичного положительного заряда
Поэтому большинству людей нужны ассоциации или критическая масса в планетарном поле, чтобы получать сигналы энергии и воспоминания о сознании и иметь возможность правильно воспринимать сигналы. Трехмерная система управления не учитывает симптомы вознесения, опыт, связанный с сознанием, или многие радикальные изменения, которые происходят у людей с этой Земли. Заземление — это форма заземления на Земле и относится к прямому контакту тела с элементами Земли. Это может быть полезно для многих людей, которые испытывают недостаток заземления и плотского дискомфорта во время планетарных изменений.
Единицей измерения ЭДС в системе единиц СИ является Вольт. ЭДС источника равна 1 вольт, если он совершает работу 1 Джоуль при перемещении заряда 1 Кулон
Для обозначения источников тока на электрических схемах используется специальное обозначение (рис. 397).
рис. 397
Электростатическое поле совершает положительную работу по перемещению положительного заряда в направлении уменьшения потенциала поля. Источник тока проводит разделение электрических зарядов − на одном полюсе накапливаются положительные заряды, на другом отрицательный. Напряженность электрического поля в источнике направлена от положительного полюса к отрицательному, поэтому работа электрического поля по перемещению положительного заряда будет положительной при его движения от «плюса» к «минусу». Работа сторонних сил, наоборот, положительна в том случае, если положительные заряды перемещаются от отрицательного полюса к положительному, то есть от «минуса» к «плюсу».
В этом принципиальное отличие понятий разности потенциалов и ЭДС, о котором всегда необходимо помнить.
Таким образом, электродвижущую силу источника можно считать алгебраической величиной, знак которой («плюс» или «минус») зависит от направления тока. В схеме, показанной на рис. 398,
рис. 398
вне источника (во внешней цепи) ток течет 2 от «плюса» источника к «минусу», в внутри источника от «минуса» к «плюсу». В этом случае, как сторонние силы источника, так и электростатические силы во внешней цепи совершают положительную работу.
Если на некотором участке электрической цепи помимо электростатических действуют и сторонние силы, то над перемещением зарядов «работают» как электростатические, так и сторонние силы. Суммарная работа электростатических и сторонних сил по перемещению единичного положительного заряда называется электрическим напряжением на участке цепи
В том случае, когда сторонние силы отсутствуют, электрическое напряжение совпадает с разностью потенциалов электрического поля.
Поясним определение напряжения и знака ЭДС на простом примере. Пусть на участке цепи, по которому протекает электрический ток, имеются источник сторонних сил и резистор (рис. 399).
рис. 399
Для определенности будем считать, что φ o > φ 1 , то есть электрический ток направлен от точки 0 к точке 1 . При подключении источника, как показано на рис. 399 а, Сторонние силы источника совершают положительную работу, поэтому соотношение (2) в этом случае может быть записано в виде
При обратном включении источника (рис. 399 б) внутри него заряды движутся против сторонних сил, поэтому работа последних отрицательна. Фактически силы внешнего электрического поля преодолевают сторонние силы. Следовательно, в этом случае рассматриваемое соотношение (2) имеет вид
Для протекания электрического тока по участку цепи, обладающему электрическим сопротивлением, необходимо совершать работу, по преодолению сил сопротивления. Для единичного положительного заряда эта работа, согласно закону Ома, равна произведению IR = U которое, естественно совпадает с напряжением на данном участке.
Заряженные частицы (как электроны, так и ионы) внутри источника движутся в некоторой , поэтому со стороны среду на них также действуют тормозящие силы, которые также необходимо преодолевать. Заряженные частицы преодолевают силы сопротивления благодаря действию сторонних сил (если ток в источнике направлен от «плюса» к «минусу») либо благодаря электростатическим силам (если ток направлен от «минуса» к «плюсу»). Очевидно, что работа по преодолению этих сил не зависит от направления движения, так как силы сопротивления всегда направлены в сторону, противоположную скорости движения частиц. Так как силы сопротивления пропорциональны средней скорости движения частиц, то работа по их преодолению пропорциональна скорости движения, следовательно, силе тока силе. Таким образом, мы можем ввести еще характеристику источника − его внутренне сопротивление r , аналогично обычному электрическому сопротивлению. Работа по преодолению сил сопротивления при перемещении единичного положительного заряда между полюсами источника равна A/q = Ir . Еще раз подчеркнем, эта работа не зависит от направления тока в источнике.
Если у вас нет доступа к природе, и вы хотите создать электрическую схему с полем Земли, вы также можете использовать праймер, который связан с человеческим телом. Электрический потенциал цепи заземления зависит от местоположения, атмосферных условий, времени суток и ночи, а также от влаги, которая расположена на поверхности Земли. Интуитивные эмпаты и звездные саженцы, которые хотят восстановить энергетическую настройку с телом планеты, должны обратить внимание на их естественные чувства, потому что они должны знать, должны ли они быть заземлены или нет.
1 Название этой физической величины неудачно − так электродвижущая сила является работой, а не силой в обычном механическом понимании. Но этот термин настолько устоялся, что изменять его не «в наших силах». К слову, сила тока то же не является механической силой! Не говоря уж о таких понятиях «сила духа», «сила воли», «божественная сила» и т.д.
2 Напомним, за направление движения электрического тока принято направление движения положительных зарядов.
В некоторых случаях из-за неорганических или внешних течений в определенных областях эта практика может оказаться нецелесообразной. Для большинства людей, которые посеяны Землей, на фазе духовной интеграции обоснование будет положительно ощущаться и будет очень полезно для тела, потому что оно будет действовать как нейромодулятор. Нейромодуляция — это процесс, в котором активность нервной системы регулируется путем регулирования физиологических уровней посредством стимуляции нейротрансмиттеров. Таким образом, заземление изменяет плотность отрицательного заряда в области энергии человека и его нервной системы и непосредственно влияет на физиологические процессы, такие как химия мозга.
Лабораторная работа
«Измерение ЭДС и внутреннего сопротивления источника тока»
Дисциплина Физика
Преподаватель Виноградов А.Б.
Нижний Новгород
Цель работы: сформировать умение определения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.
Земля посылает электромагнитные сигналы для поддержки человеческих тел при адаптации к ее вознесению, и этот сигнал позволяет человеческой нервной системе лучше адаптироваться к требованиям, предъявляемым к телу и мозгу во время интенсивных изменений сознания. Когда мы хотим восстановить электрический баланс активности мозга, может быть особенно полезно окружить природу, сосредоточиться на глубоком дыхании и соединиться с Землей или с элементом воды.
Почки — это органы, которые питают энергию. В настоящее время население людей переживает эпидемию заболеваний почек, вызванных неспособностью органов быстро адаптироваться к новым обстоятельствам, плохого признания событий, изменяющих жизнь, сердечных заболеваний, перегрузки токсичными химическими веществами и негативных эмоций. Целью почек является удаление вредных метаболических продуктов, выделяемых мочевым пузырем, и поддержание надлежащей химии крови и давления, поскольку они контролируют все химические вещества, растворенные в кровотоке.
Оборудование: выпрямитель ВУ-4М, амперметр, вольтметр, соединительные провода, элементы планшета №1: ключ, резистор R 1 .
Теоретическое содержание работы .
Внутреннее сопротивление источника тока.
При прохождении тока по замкнутой цепи, электрически заряженные частицы перемещаются не только внутри проводников, соединяющих полюса источника тока, но и внутри самого источника тока. Поэтому в замкнутой электрической цепи различают внешний и внутренний участки цепи. Внешний участок цепи составляет вся та совокупность проводников, которая подсоединяется к полюсам источника тока. Внутренний участок цепи — это сам источник тока. Источник тока, как и любой другой проводник, обладает сопротивлением. Таким образом, в электрической цепи, состоящей из источника тока и проводников с электрическим сопротивлением R , электрический ток совершает работу не только на внешнем, но и на внутреннем участке цепи. Например, при подключении лампы накаливания к гальванической батарее карманного фонаря электрическим током нагреваются не только спираль лампы и подводящие провода, но и сама батарея. Электрическое сопротивление источника тока называется внутренним сопротивлением. В электромагнитном генераторе внутренним сопротивлением является электрическое сопротивление провода обмотки генератора. На внутреннем участке электрической цепи выделяется количество теплоты, равное
Когда почки ослаблены и перегружены, в крови и тканях накапливаются токсичные отходы, а также химические вещества, которые невозможно фильтровать надлежащим образом. Почечная недостаточность увеличивается в Соединенных Штатах на 5% в год, при этом в качестве терапии используют почечный диализ или трансплантацию. Десять процентов населения имеют некоторую форму диабета и неврологического дискомфорта, и это число, по-видимому, неуклонно растет — у взрослых и у детей. Что случилось с нашими почками?
Восточная медицинская философия знает, что почки питают другие органы тела. Они действуют как корни жизни, которые отвечают за защиту организма и распределение энергии во всех органах, репродуктивных функциях и всего организма. Почки — это органы взаимоотношений, поэтому они страдают от проблем с межличностными и сексуальными отношениями, которые могут возникнуть в результате отсутствия поддержки у других или чувства нелюбимой или даже из-за отсутствия физической чувствительности. Эмоции циркулируют в личной энергетической области, и когда она будет выпущена, у вас может возникнуть ощущение течения, благодаря которому вы ощущаете эмоции.
где r — внутреннее сопротивление источника тока.
Полное количество теплоты, выделяющееся при протекании постоянного тока в замкнутой цепи, внешний и внутренний участки которой имеют сопротивления, соответственно равные R и r , равно
Всякую замкнутую цепь можно представить как два последовательно соединенных резистора с эквивалентными сопротивлениями R и r . Поэтому сопротивление полной цепи равно сумме внешнего и внутреннего сопротивлений:
. Поскольку при последовательном соединении сила тока на всех участках цепи одинакова, то через внешний и внутренний участок цепи проходит одинаковый по величине ток. Тогда по закону Ома для участка цепи падение напряжений на ее внешнем и внутреннем участках будут соответственно равны:
Это позволяет вам освобождать эмоциональную боль и страх и избавляет вас от хронических проблем с почками, открывая для себя большее эмоциональное и духовное расширение энергии. Когда это наоборот, когда сердце закрыто от боли и страха, что блокирует эмоции, оно влияет на функцию управления жидкостью через почки и нарушает распределение жизненной энергии, необходимой для заземленного, здорового и сбалансированного ума и тела.
Более того, когда наше сердце исцеляется, внутри горит пламя, которое также питается жизненной энергией, хранящейся в почках. Треугольный соединитель соединяет сердце с каждой почкой, которая работает в светящемся теле, как электрическая цепь. В основании этого треугольника слева и справа находятся почки, а верхняя точка связана с сердцем. Когда сердце исцеляется, пламя в сердце и почках одновременно активирует конфигурацию сердца во внутреннем двойном пламени. Двойное пламя соответствует восстановленному энергетическому балансу между энергией самца и женщины, т.е. структурой света, созданного в комплексе сердца.
и
(3)
Электродвижущая сила.
Полная работа сил электростатического поля при движении зарядов по замкнутой цепи постоянного тока равна нулю. Следовательно, вся работа электрического тока в замкнутой электрической цепи оказывается совершенной за счет действия сторонних сил, вызывающих разделение зарядов внутри источника и поддерживающих постоянное напряжение на выходе источника тока. Отношение работы
, совершаемой сторонними силами по перемещению заряда q вдоль цепи, к значению этого заряда называется электродвижущей силой источника (ЭДС) :
Поэтому, когда два огня зажигаются в сердце, жизненно важная сущность, хранящаяся в почках, помогает переносить чи-пламя по всему физическому телу, чтобы соединиться с духовным пламенем монадического тела. Монада — это большее пламя духа, а физическое тело — меньшее пламя жизненной сущности или жизненной силы. Когда эти два огня зажигаются и объединяются, пламя взрывается от сердца, которое посылает огонь, чтобы поддержать рост сущности жизни, создаваемой почками. В основном, почки помогают построить внутреннее светящееся тело, необходимое для встраивания монадического тела.
, (4)
— переносимый заряд.
ЭДС выражается в тех же единицах, что и напряжение или разность потенциалов, т. е. в вольтах:
.
Закон Ома для полной цепи.
Любые визуальные упражнения, направленные на создание жизненной силы энергии в низших диенах и вызывают энергию для циркуляции у подножия ног, укрепляют способность почек хранить жизненно важную сущность, помогают исправить механизм заземления и выполнять функции физической очистки крови. Существуют некоторые потенцирующие агенты для почек и трав, которые являются общими для восточной медицины и полезны для тонизирования функции почек, особенно если есть проблема с заземлением или центрированием сердечника.
Почечная недостаточность вызывает выработку надпочечников. Надпочечники — это железы, которые производят много гормонов, и хорошо известно, что под давлением они перекачивают кортизол в кровоток, что приводит к тому, что человеческая нервная система переходит в состояние борьбы или полета. Адреналин обычно продуцируется как надпочечниками, так и некоторыми нейронами, которые также могут активироваться эмоциональными реакциями. Каждая эмоциональная реакция имеет поведенческий компонент, компонент вегетативной нервной системы, секрецию железы или гормональный фактор.
Если в результате прохождения постоянного тока в замкнутой электрической цепи происходит только нагревание проводников, то по закону сохранения энергии полная работа электрического тока в замкнутой цепи, равная работе сторонних сил источника тока, равна количеству теплоты, выделившейся на внешнем и внутреннем участках цепи:
Гормональные факторы, связанные со стрессом и эмоциональной болью, включают высвобождение адреналина и реакции надпочечников — в ответ на чувства, основанные на страхе, контролируемые симпатической нервной системой. Основная эмоция, которая выделяет адреналин в кровь, — это страх.
Кроме того, надпочечники играют важную роль в реагировании на борьбу или бегство, увеличивая приток крови к мышцам и сердцу, а затем учащиеся расширяются и уровень сахара в крови увеличивается. Адреналин закачивается в кровоток, когда человек провоцируется на террористические акты или страх, чтобы произвести как можно больше негативной эмоциональной энергии, что может быть основной причиной того, что надпочечники полностью истощены у большинства людей. Когда человек не исправляет это состояние и все еще накачивает адреналин или другие гормоны стресса в кровоток, нервная система замерзает, состояние шока и онемения.
. (5)
Из выражений (2), (4) и (5) получаем:
. (6)
, то
, (7)
В какой-то момент, когда вы испытываете постоянную боль или страх, из-за чрезмерной нагрузки адреналина, тело и нервная система попадают в состояние онемения, которое отключает эмоциональные реакции, закрывая сердце. Надпочечники находятся в верхней части каждой почки, поэтому они непосредственно подвержены истощению почек, что, естественно, приводит к выходу надпочечников. Если мы делаем что-то действительно нездоровое для нашего духа, и наша повседневная работа не соответствует тому, кто мы есть, он также истощает почки, адреналин и жизненную силу.
. (8)
Сила тока в электрической цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна сумме электрических сопротивлений внешнего и внутреннего участков цепи. Выражение (8) называется законом Ома для полной цепи.
Когда нам приходится сталкиваться с трудными стрессовыми факторами на работе, в отношениях или в других ситуациях, организм может подвергаться глубокому бессознательному эмоциональному стрессу. Мы чувствуем себя беспомощными и расстроены тем, что мы должны просто работать, чтобы выполнить финансовые обязательства или выжить. Наше тело дает нам сообщение из-за чрезмерного истощения, что мы уже не можем жить таким же образом, мы должны вносить изменения, и первое изменение должно состоять в том, чтобы осуществить сознание через смерть эго.
Таким образом, с точки зрения физики Закон Ома выражает закон сохранения энергии для замкнутой цепи постоянного тока.
Порядок выполнения работы .
Подготовка к выполнению работы.
Перед вами на столах находится минилаборатория по электродинамике. Её вид представлен в л. р. № 9 на рисунке 2.
Слева находятся миллиамперметр, выпрямитель ВУ-4М, вольтметр, амперметр. Справа закреплен планшет № 1 (см. рис. 3 в л. р. № 9). В задней секции корпуса размещаются соединительные провода цветные: красный провод используют для подключения ВУ-4М к гнезду «+» планшета; белый провод — для подключения ВУ-4М к гнезду «-»; желтые провода — для подключения к элементам планшета измерительных приборов ; синие — для соединения между собой элементов планшета. Секция закрыта откидной площадкой. В рабочем положении площадка располагается горизонтально и используется в качестве рабочей поверхности при сборке экспериментальных установок в опытах.
Планетарный контроль над человеческими почками Чи. Мы должны стремиться к восстановлению сердечного центра и превращению почек в более высокую цель, связанную с вознесением тела. Существуют оверлеи, кодирующие человеческие тела для порабощения, установленные во время рождения, в записи последовательности трансдукции в теле проявления ядра или в Древе Жизни. Основной шаблон проявления сетки дерева имеет набор инструкций для контроля функций органов и желез на уровне каждого измерения, поскольку железы выделяют вещества и гормоны, которые позволяют человеческому сознанию двигаться быстрее между измерениями.
2. Ход работы.
В ходе работы вы освоите метод измерения основных характеристик источника тока, используя закон Ома для полной цепи, который связывает силу тока I в цепи, ЭДС источника тока , его внутреннее сопротивление r и сопротивление внешней цепи R соотношением:
В землях Соединенного Королевства ключи от пробуждения структур Альбиона скрыты, и они являются гигантскими спящими существами. Теги используются для руководства людьми на Земле для будущих временных линий для работы в рабских колониях или в различных галактических местах торговли людьми, которые контролируются этими внеземными коррумпированными конгломератами и группами драконов.
Группы Черного Солнца Ориона оставляли за собой право на некоторые человеческие тела, генетический материал и человеческое Древо Жизни, и именно поэтому они контролируют его. Благодаря этому им легче контролировать и контролировать информацию, связанную со структурой души и многомерной анатомией. Это драконовцы, которые воруют из духовных частей тела, а также из органов и желез.
. (9)
1 способ.
Схема экспериментальной установки показана на рисунке 1.
Внимательно изучите её. При разомкнутом ключе В источник замкнут на вольтметр, сопротивление которого много больше внутреннего сопротивления источника (r R ). В этом случае ток в цепи настолько мал, что можно пренебречь значением падения напряжения на внутреннем сопротивлении источника
, и ЭДС источника с пренебрежимо малой погрешностью равна напряжения на его зажимах , которое измеряется вольтметром, т.е.
. (10)
Таким образом, ЭДС источника определяется по показаниям вольтметра при разомкнутом ключе В.
Если ключ В замкнуть, вольтметр покажет падение напряжения на резисторе R :
. (11)
Тогда на основании равенств (9), (10) и (11) можно утверждать, что
(12)
Из формулы (12) видно, что для определения внутреннего сопротивления источника тока необходимо, кроме его ЭДС, знать силу тока в цепи и напряжение на резисторе R при замкнутом ключе.
Силу тока в цепи можно измерить при помощи амперметра. Проволочный резистор изготовлен из нихромовой проволоки и имеет сопротивление 5 Ом.
Соберите цепь по схеме, показанной на рисунке 3.
После того, как цепь будет собрана, необходимо поднять руку, позвать учителя, чтобы он проверил правильность сборки электрической цепи. И если цепь собрана правильно, то приступайте к выполнению работы.
При разомкнутом ключе В снимите показания вольтметра и занесите значение напряжения в таблицу 1. Затем замкните ключ В и опять снимите показания вольтметра, но уже и показания амперметра. Занесите значение напряжения и силы тока в таблицу 1.
Сформулируйте закон Ома для полной цепи.
Если бы мы не знали значения сопротивлений проволочных резисторов, то можно ли было бы использовать второй способ и что для этого надо сделать (может нужно, например, включить в цепь какой-нибудь прибор)?
Уметь собирать электрические цепи, используемые в работе.
Литература
Кабардин О. Ф.. Справ. Материалы: Учеб. Пособие для учащихся.-3-е изд.-М.:Просвещение,1991.-с.:150-151.
Справочник школьника. Физика/ Сост. Т. Фещенко, В. Вожегова.–М.: Филологическое об-щество «СЛОВО», ООО «Фирма» «Издательство АСТ», Центр гуманитарных наук при ф-те журна-листики МГУ им. М. В. Ломоносова, 1998. — с.: 124,500-501.
Самойленко П. И.. Физика (для нетехнических специальностей): Учебн. для общеобразоват. учреждений сред. Проф. Образования/ П. И.Самойленко, А. В. Сергеев.-2-е изд., стер.-М.: Издательский центр «Академия», 2003-с.: 181-182.
Цель работы: Научиться экспериментальным путем определять ЭДС, и внутреннее сопротивление источника тока.
Приборы и оборудование: Источники электрической энергии, амперметр (до 2А с делением до 0,1А), вольтметр (постоянного до 3А с делением до 0,3В), магазин (сопротивления до 10 Ом) ключ, соединительные провода.
ТЕОРИЯ:
Для поддержания тока в проводнике необходимо, чтобы разность потенциалов (напряжение) на его концах была неизменной. Для этого используется источник тока. Разность потенциалов на его полюсах образуется вследствие разделения зарядов на положительные и отрицательные. Работу по разделению зарядов выполняют сторонние силы (не электрического происхождения).
Величина, измеряемая работой, совершенной сторонними силами при перемещении единичного положительного электрического заряда внутри источника тока, называется электродвижущей силой источника тока (ЭДС) и выражается в вольтах.
Когда цепь замыкается, разделенные в источнике тока заряды образуют электрическое поле, которое перемещает заряды по внешней цепи; внутри же источника тока заряды движутся навстречу полю под действием сторонних сил. Таким образом, энергия, запасенная в источнике тока, расходуется на работу по перемещению заряда в цепи с внешним R и внутренним r сопротивлениями.
ХОД РАБОТЫ
1. Собрать электрическую цепь как показано на схеме.
2. Измерить ЭДС источника электрической энергии замкнув его на вольтметр (схема).
3. Измерить силу тока и падение напряжения на заданном сопротивлении.
| № | Е | U | I | R | r | rcр |
| 1. | ||||||
| 2. | ||||||
| 3. |
4. Вычислить внутреннее сопротивление по закону Ома для всей цепи.
5. Произвести опыты с другими сопротивлениями и вычислить внутреннее сопротивление элемента.
6. Вычислить среднее значение внутреннего сопротивления элемента.
7. Результаты всех измерений и вычислений записать в таблицу.
8. Найти абсолютную и относительную погрешность.
9. Сделать вывод.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Укажите условия существования электрического тока в проводнике.
2. Какова роль источника электрической энергии в электрической цепи?
3. От чего зависит напряжение на зажимах источника электрической энергии?
ЛАБОРАТОРНАЯ РАБОТА № 7
ОПРЕДЕЛЕНИЕ ЭЛЕКТРОХИМИЧЕСКОГО ЭКВИВАЛЕНТА МЕДИ.
Цель работы : научиться на практике рассчитывать электрохимический эквивалент меди.
Оборудование: Весы с разновесом, амперметр, часы., источник электрической энергии, реостат, ключ, медные пластины (электроды), соединительные провода, электролитическая ванна с раствором медного купороса.
Теория
Процесс, при котором молекулы солей, кислот и щелочей при растворении в воде или других растворителях распадаются на заряженные частицы (ионы), называется электролитической диссоциацией, получившийся при этом раствор с положительными и отрицательными ионами называется электролитом.
Если в сосуд с электролитом поместить пластины (электроды), соединенные с зажимами источника тока (создать в электролите электрическое поле), то положительные ионы будут двигаться к катоду, а отрицательные — к аноду. Следовательно, в растворах кислот, солей и щелочей электрический заряд будет перемещаться вместе с частицами вещества. У электродов при этом происходит окислительно-восстановительные реакции, при которых на них выделяется вещество. Процесс прохождения электрического тока через электролит, сопровождающийся химическими реакциями называется электролизом.
Для электролиза справедлив закон Фарадея: масса выделившегося вещества на электроде прямо пропорциональна заряду, прошедшему через электролит:
где k-электрохимический эквивалент-количествовещества, выделенное при прохождении через электролит 1 Кл электричества. Измерив силу тока в цепи, время его прохождения и массу выделившегося на катоде вещества можно определить электрохимический эквивалент (1с выражается в кг/Кл).
где m-масса меди, выделившейся на катоде; I-сила тока в цепи; t- время пропускания тока в цепи.
Соберите электрическую цепь по схеме.
1. Одну из пластин, которая будет катодом, (если пластина мокрая, ее надо подсушить) тщательно взвесить с точностью до 10мг и записать результат в таблицу.
2. Вставить электрод в электролитическую ванну и составить электрическую цепь согласно схеме.
3. Отрегулировать реостатом ток, чтобы величина его не превышала 1А на 50см 2 погруженной части катодной пластины.
4. Замкнуть цепь на 15-20 минут.
5. Разомкнуть цепь, вынуть катодную пластинку, смыть с нее остатка раствора и высушить под рукосушителем.
6. Взвесить высушенную пластину с точностью до 10мг.
7. Значение тока, время опыта, увеличение в массе катодной пластину записать в таблицу и определить электрохимический эквивалент.
Оценка погрешностей.
.
Относительная погрешность:
.
, следовательно .
После этого дается результат в виде: .
Сравните полученный результат с табличным.
Контрольные вопросы.
1. Что такое электролитическая диссоциация, электролиз?
2. До каких пор будет происходить электролиз медного купороса, если оба электрода медные? Оба электрода угольные?
3. Быстрее или медленнее пойдет электролиз, если один из медных электродов заменить цинковым?
На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .
Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).
Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.
При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).
В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:
— электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;
— термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;
— фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;
— химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.
Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:
ɛ = A ст /q ,
где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.
Электродвижущую силу выражают в вольтах.
Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.
Внутреннее сопротивление источника тока.
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .
В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
Закон Ома для полной цепи ❤️
1. Источник тока
При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.
Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического
поля. Таким участком цепи является источник тока (рис. 59.1).В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом — отрицательный.
Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
В химических источниках тока сторонние силы имеют химическую
природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового.Медный электрод станет положительным полюсом источника тока, а цинковый — отрицательным.
В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Электродвижущая сила источника тока
В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.
Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
Ξ = Aстор/q. (1)
(Это название не совсем удачно, потому что ЭДС — не «сила» в механическом смысле, а энергетическая характеристика источника.)
ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.
2. Закон Ома для полной цепи
Если сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде
Aстор = ξIt. (2)
При этом во внешней цепи сопротивлением R выделяется количество теплоты
Qвнеш = I2Rt, (3)
А внутри источника тока выделяется количество теплоты
Qвнутр = I2rt, (4)
Где r — сопротивление источника, которое называют его внутренним сопротивлением.
Из закона сохранения энергии следует, что
Qвнеш + Qвнутр = Aстор. (5)
? 1. Докажите, что из формул (2) — (5) следует:
I = ξ / (R + r). (6)
Это соотношение называют законом Ома для полной цепи.
Сумму сопротивлений R + r называют полным сопротивлением цепи.
? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом. а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом? б) Какова максимально возможная сила тока в цепи?
При каком сопротивлении внешней цепи это имеет место?
? 3. При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А. а) Чему равно внутреннее сопротивление источника? б) Чему равна ЭДС источника?
Напряжение на полюсах источника
Закон Ома для полной цепи можно записать в виде
Ξ = IR + Ir. (7)
Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:
IR = U.
Поэтому формулу (7) можно записать в виде
U = ξ — Ir. (8)
Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.
Поставим опыт Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате.
Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.
? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока. а) Чему равна ЭДС этого источника тока? б) Чему равна наибольшая сила тока? в) Чему равно внутреннее сопротивление источника тока? г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна? е) Чему равно внешнее сопротивление при I = 1,5 А?
Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.
Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.
? 5. Покажите, что сила тока короткого замыкания выражается формулой
Iка = ξ/r. (9)
Подсказка. Воспользуйтесь законом Ома для полной цепи.
Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А. а) Как изменилось полное сопротивление цепи? б) Чему равно внутреннее сопротивление батарейки?
Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.
? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В. а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным. б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.
3. КПД источника тока
Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:
Aпол = I2Rt.
Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку
Aстор = I2Rt + I2rt,
Получаем для отношения полезной работы к работе сторонних сил:
Η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).
Это отношение, выраженное в процентах, называют КПД источника тока.
? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?
Дополнительные вопросы и задания
9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении — 2 А и 12 В.
а) Как сдвинули ползунок реостата между первым и вторым измерениями — влево или вправо? б) Чему равны ЭДС источника тока и его внутреннее сопротивление? в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?
10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт. а) Чему равна ЭДС источника тока? б) Чему равно внутреннее сопротивление источника тока? в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?
Электротехника Лекция 3 -4 Преподаватель Никулина Светлана Викторовна
Электротехника Лекция 3 -4 Преподаватель: Никулина Светлана Викторовна
Электротехника Что изучает электротехника? Это область науки и техники, изучающая электрические и магнитные явления и их использование в практических целях получения, преобразования, передачи и потребления электрической энергии.
Какие токи и напряжения считаются относительно безопасными для человека? а)меньше 0, 1 А и больше 24 В б) больше 5 м. А и 12 В в)меньше 50 м. А и 36 В г)меньше 100 м. А и 100 В
Что такое электрический ток в металлах? a) b) c) d) Хаотичное движение электронов Упорядоченное движение атомов Направленное движение заряженных частиц Направленное движение электронов
Почему именно электроны участвуют в создании тока в металлах? a) b) c) d) Их больше, чем протонов; Они имеют отрицательный заряд; Они легче протонов; Они могут покидать свои орбиты и становиться свободными.
Почему именно электроны участвуют в создании тока в металлах?
Что такое сила тока в металлах?
Что такое плотность тока в металлах?
Потенциал – энергетическая характеристика электрического поля. Она определяет энергию, которую приобретает заряженная частица в электрическом поле.
Найдите соответствие Напряжение R Ампер В Сила тока P Вольт А Сопротивление U Ватт Ом ЭДС G Вольт См Проводимость E Сименс Вт Мощность I Ом В
ЭДС источника выражается формулой: А.
Какой из проводников. Медный или алюминиевый, при одинаковых длине и площади поперечного сечения нагреется сильнее: А) при одном и том же токе; В) при одном и том же напряжении?
При одинаковом токе Нагрев проводника обусловлен работой электрического тока, которая определяется силой тока и сопротивлением проводника. Нагрев алюминиевого проводника будет больше.
При одинаковом напряжении Нагрев проводника обусловлен работой электрического тока, которая определяется силой тока и сопротивлением проводника. Нагрев медного проводника будет больше.
Проверим решение задачи, заданной на дом
Химические источники тока Принцип работы Окислительно-восстановительная реакция, протекающая между веществами, обладающими свойствами окислителя и восстановителя, сопровождаются выделением электронов, движение которых образует электрический ток. Однако, чтобы использовать его энергию, необходимо создать условия для прохождения электронов через внешнюю цепь, в противном случае она при простом смешивании окислителя и восстановителя выделяется во внешнюю среду теплом. Поэтому все химические источники тока имеют два электрода: • анод, на котором происходит окисление; • катод, осуществляющий восстановление вещества.
Когда внешняя и внутренняя цепь разомкнуты, то на электродах протекают два процесса: переход ионов из металла электрода в электролит и переход ионов из электролита в кристаллическую решетку электродов. Скорости протекания этих процессов одинаковы и на каждом электроде накапливаются потенциалы напряжения противоположных знаков.
Если их соединить через солевой мостик и приложить нагрузку, то возникнет электрическая цепь. По внутреннему контуру электрический ток создается движением ионов между электродами через электролит и солевой мостик. По внешней цепи возникает движение электронов по направлению от анода на катод.
Способы классификации Одна часть химических источников тока может повторно использоваться, а другая нет. Этот принцип взят за основу их классификации.
Первичные химические источники тока не поддерживают повторную зарядку, хотя более точно это положение можно сформулировать подругому: ее проведение экономически не целесообразно. Аккумуляторы успешно перезаряжаются приложением внешней электрической энергии. Благодаря этой возможности их называют вторичными источниками тока. Они способны выдерживать сотни и тысячи циклов заряда-разряда. ЭДС аккумулятора может быть в пределах 1, 0÷ 1, 5 вольта. Электрохимические генераторы работают по принципу гальванических элементов, но у них для проведения электрохимической реакции вещества поступают извне, а все выделяющиеся продукты удаляются из электролита. Это позволяет организовать непрерывный процесс.
Принципы заряда аккумуляторов Литий ионные модели( материалом положительного электрода используется Li. MO 2 (M Co, Ni, Mn), а отрицательного — графит)
Электромашинные генераторы
Термогенераторы
Пьезоэлектрические источники
Электрическая цепь — это совокупность электротехнических устройств, объектов (источников, приемников электроэнергии, коммутационных, защитных аппаратов и пр. ) и соединяющих их проводников, представляющих собой путь для прохождения электрического тока. Протекание электрического тока возможно только в замкнутой ЭЦ; при ее размыкании на любом участке протекание тока прекратится. Графическое изображение электрической цепи с помощью условных обозначений ее элементов называется электрической схемой цепи.
Электрические цепи разветвленные. Во всех элементах неразветвленной цепи действует один и тот же ток. неразветвленные имеет в своем составе ветви, узлы, контуры. Ветвь — это участок цепи, состоящий из последовательно соединенных элементов и заключенный между двумя узлами. В каждой ветви существует свой ток. Узел — это точка в электрической схеме цепи, где гальванически соединяются не менее трех ветвей. Любой замкнутый путь на схеме называется контуром. Независимым называется контур, содержащий хотя бы одну ветвь, не включенную в иной контур.
Общие сведения о преобразовании схем Однотипные элементы электрической цепи соединенные последовательно или параллельно можно заменить одним общим (эквивалентным) элементом. Под «эквивалентным элементом» подразумевается тот факт, что замена не повлияет на величину токов и напряжений в остальной части схемы. Значение параметров эквивалентного элемента определяются исходя из свойств каждого соединения. Подобное преобразование соединений элементов осуществляют для упрощения электрической схемы, а следовательно и упрощения решения электротехнической задачи.
Последовательное соединение элементов Соединение элементов электрической цепи называют последовательным, если через них протекает один и тот же ток.
Параллельное соединение элементов Соединение нескольких элементов называют параллельным, если напряжение на каждом из элементов имеет одно и то же значение.
Смешанное соединение элементов представляет собой сочетание рассмотренных последовательного и параллельного соединений.
Расчет простых электрических цепей К простым относят электрические цепи, которые содержат либо один источник электрической энергии, либо несколько находящихся в одной ветви электрической цепи. Алгоритм решения: 1. Упрощаем схему последовательно преобразовав все пассивные элементы схемы в один эквивалентный резистор. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения.
Для этого необходимо выделять участки схемы, на которых резисторы соединены последовательно или параллельно, и по известным формулам заменять их эквивалентными резисторами (сопротивлениями). Цепь постепенно упрощают и приводят к наличию в цепи одного эквивалентного резистора. пример
Расчет простых электрических цепей К простым относят электрические цепи, которые содержат либо один источник электрической энергии, либо несколько находящихся в одной ветви электрической цепи. Алгоритм решения: 1. Упрощаем схему последовательно преобразовав все пассивные элементы схемы в один эквивалентный резистор. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения. 2. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения.
Расчет простых электрических цепей Алгоритм решения: 1. Упрощаем схему последовательно преобразовав все пассивные элементы схемы в один эквивалентный резистор. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения. 2. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения. 3. В итоге мы приводим любую простую электрическую схему к следующему виду: Теперь есть возможность применить закон Ома — соотношение и фактически определить значение тока протекающего через источник электрической энергии. 4. Теперь поэтапно эквивалентную схему преобразовывают к начальному виду. После каждого пункта «усложнения» схемы используя законы Ома и Кирхгофа определяют токи и напряжения на отдельных участках схемы.
Пример решения:
Пример решения:
10.2: Электродвижущая сила — Physics LibreTexts
Цели обучения
К концу раздела вы сможете:
- Опишите электродвижущую силу (ЭДС) и внутреннее сопротивление батареи
- Объясните основную работу аккумулятора
Если вы забыли выключить автомобильные фары, они постепенно тускнеют по мере разрядки аккумулятора. Почему они не мигают внезапно, когда разрядился аккумулятор? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи.Причина снижения выходного напряжения для разряженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.
Введение в электродвижущую силу
Voltage имеет множество источников, некоторые из которых показаны на рисунке \ (\ PageIndex {2} \). Все такие устройства создают разность потенциалов и могут подавать ток, если подключены к цепи.Особый тип разности потенциалов известен как электродвижущая сила (ЭДС) . ЭДС — это вовсе не сила, но термин «электродвижущая сила» используется по историческим причинам. Он был изобретен Алессандро Вольта в 1800-х годах, когда он изобрел первую батарею, также известную как гальваническая батарея . Поскольку электродвижущая сила не является силой, принято называть эти источники просто источниками ЭДС (произносимых буквами «э-э-э-эфф»), а не источниками электродвижущей силы.
Рисунок \ (\ PageIndex {1} \): различные источники напряжения. а) ветряная электростанция Бразос в Флуванна, штат Техас; (б) Красноярская плотина в России; (c) солнечная ферма; (d) группа никель-металлогидридных батарей. Выходное напряжение каждого устройства зависит от его конструкции и нагрузки. Выходное напряжение равно ЭДС только при отсутствии нагрузки. (кредит a: модификация работы «Leaflet» / Wikimedia Commons; кредит b: модификация работы Алекса Полежаева; кредит c: модификация работы Министерства энергетики США; кредит d: модификация работы Тиаа Монто)Если Электродвижущая сила — это вообще не сила, тогда что такое ЭДС и что является источником ЭДС? Чтобы ответить на эти вопросы, рассмотрим простую схему лампы 12 В, подключенной к батарее 12 В, как показано на рисунке \ (\ PageIndex {2} \).Батарея , может быть смоделирована как устройство с двумя выводами, которое поддерживает один вывод с более высоким электрическим потенциалом, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.
Рисунок \ (\ PageIndex {2} \): Источник ЭДС поддерживает на одном выводе более высокий электрический потенциал, чем на другом выводе, действуя как источник тока в цепи.Когда источник ЭДС не подключен к лампе, нет чистого потока заряда внутри источника ЭДС. Как только батарея подключена к лампе, заряды перетекают от одной клеммы батареи через лампу (в результате чего лампа загорается) и обратно к другой клемме батареи. Если мы рассмотрим протекание положительного (обычного) тока, положительные заряды покидают положительный вывод, проходят через лампу и попадают в отрицательный вывод.
Положительный поток тока полезен для большей части анализа схем в этой главе, но в металлических проводах и резисторах наибольший вклад в ток вносят электроны, протекающие в направлении, противоположном положительному потоку тока.Поэтому более реалистично рассматривать движение электронов для анализа схемы на рисунке \ (\ PageIndex {2} \). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя выводами, отрицательные заряды (электроны) должны перемещаться с положительного вывода на отрицательный. Источник ЭДС действует как накачка заряда, перемещая отрицательные заряды от положительного вывода к отрицательному для поддержания разности потенциалов.Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.
Сила, действующая на отрицательный заряд электрического поля, действует в направлении, противоположном электрическому полю, как показано на рисунке \ (\ PageIndex {2} \). Чтобы отрицательные заряды переместились на отрицательный вывод, необходимо провести работу с отрицательными зарядами. Для этого требуется энергия, которая возникает в результате химических реакций в батарее. Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами.ЭДС равна работе, выполняемой над зарядом на единицу заряда \ (\ left (\ epsilon = \ frac {dW} {dq} \ right) \) при отсутствии тока. Поскольку единицей измерения работы является джоуль, а единицей заряда — кулон, единицей измерения ЭДС является вольт \ ((1 \, V = 1 \, J / C) \).
Напряжение на клеммах \ (V_ {клемма} \) батареи — это напряжение, измеренное на клеммах батареи, когда к клемме не подключена нагрузка. Идеальная батарея — это источник ЭДС, который поддерживает постоянное напряжение на клеммах, независимо от тока между двумя клеммами.Идеальная батарея не имеет внутреннего сопротивления, а напряжение на клеммах равно ЭДС батареи. В следующем разделе мы покажем, что у реальной батареи есть внутреннее сопротивление, а напряжение на клеммах всегда меньше, чем ЭДС батареи.
Происхождение потенциала батареи
ЭДС батареи определяется сочетанием химических веществ и составом выводов батареи. Свинцово-кислотный аккумулятор , используемый в автомобилях и других транспортных средствах, является одним из наиболее распространенных сочетаний химических веществ.На рисунке \ (\ PageIndex {3} \) показана одна ячейка (одна из шести) этой батареи. Катодная (положительная) клемма ячейки соединена с пластиной из оксида свинца, а анодная (отрицательная) клемма подключена к свинцовой пластине. Обе пластины погружены в серную кислоту, электролит для системы.
Рисунок \ (\ PageIndex {3} \): Химические реакции в свинцово-кислотном элементе разделяют заряд, отправляя отрицательный заряд на анод, который соединен со свинцовыми пластинами. Пластины из оксида свинца подключаются к положительному или катодному выводу ячейки.Серная кислота проводит заряд, а также участвует в химической реакции.Небольшое знание того, как взаимодействуют химические вещества в свинцово-кислотной батарее, помогает понять потенциал, создаваемый батареей. На рисунке \ (\ PageIndex {4} \) показан результат одной химической реакции. Два электрона помещаются на анод , что делает его отрицательным, при условии, что катод подает два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона.Короче говоря, разделение заряда было вызвано химической реакцией.
Обратите внимание, что реакция не происходит, если нет замкнутой цепи, позволяющей подавать два электрона на катод. Во многих случаях эти электроны выходят из анода, проходят через сопротивление и возвращаются на катод. Также обратите внимание, что, поскольку в химических реакциях участвуют вещества, обладающие сопротивлением, невозможно создать ЭДС без внутреннего сопротивления.
Рисунок \ (\ PageIndex {4} \): В свинцово-кислотной батарее два электрона прижимаются к аноду элемента, а два электрона удаляются с катода элемента.В результате химической реакции в свинцово-кислотной батарее два электрона помещаются на анод и два электрона удаляются с катода. Для продолжения требуется замкнутая цепь, так как два электрона должны быть доставлены на катод.Внутреннее сопротивление и напряжение на клеммах
Величина сопротивления току внутри источника напряжения называется внутренним сопротивлением . Внутреннее сопротивление батареи r может вести себя сложным образом. Обычно она увеличивается по мере разряда батареи из-за окисления пластин или снижения кислотности электролита.Однако внутреннее сопротивление также может зависеть от величины и направления тока через источник напряжения, его температуры и даже его предыстории. Например, внутреннее сопротивление перезаряжаемых никель-кадмиевых элементов зависит от того, сколько раз и насколько глубоко они были разряжены. Простая модель батареи состоит из идеализированного источника ЭДС \ (\ epsilon \) и внутреннего сопротивления r (рисунок \ (\ PageIndex {5} \)).
Рисунок \ (\ PageIndex {5} \): Батарею можно смоделировать как идеализированную ЭДС \ ((\ epsilon) \) с внутренним сопротивлением ( r ).Напряжение на клеммах аккумулятора равно \ (V_ {terminal} = \ epsilon — Ir \).Предположим, что внешний резистор, известный как сопротивление нагрузки R , подключен к источнику напряжения, например батарее, как показано на рисунке \ (\ PageIndex {6} \). На рисунке показана модель аккумулятора с ЭДС ε, внутренним сопротивлением r и нагрузочным резистором R , подключенным к его клеммам. При обычном протекании тока положительные заряды покидают положительную клемму батареи, проходят через резистор и возвращаются к отрицательной клемме батареи.Напряжение на клеммах аккумулятора зависит от ЭДС, внутреннего сопротивления и силы тока и равно
.Примечание
\ [V_ {терминал} = \ epsilon — Ir \]
При заданной ЭДС и внутреннем сопротивлении напряжение на клеммах уменьшается по мере увеличения тока из-за падения потенциала Ir внутреннего сопротивления.
Рисунок \ (\ PageIndex {6} \): Схема источника напряжения и его нагрузочного резистора R . Поскольку внутреннее сопротивление r последовательно с нагрузкой, оно может значительно повлиять на напряжение на клеммах и ток, подаваемый на нагрузку.График разности потенциалов на каждом элементе цепи показан на рисунке \ (\ PageIndex {7} \). Через цепь проходит ток I , а падение потенциала на внутреннем резисторе равно Ir . Напряжение на клеммах равно \ (\ epsilon — Ir \), что равно падению потенциала на нагрузочном резисторе \ (IR = \ epsilon — Ir \). Как и в случае с потенциальной энергией, важно изменение напряжения. Когда используется термин «напряжение», мы предполагаем, что это на самом деле изменение потенциала, или \ (\ Delta V \).Однако \ (\ Delta \) часто для удобства опускается.
Рисунок \ (\ PageIndex {7} \): график напряжения в цепи батареи и сопротивления нагрузки. Электрический потенциал увеличивает ЭДС батареи из-за химических реакций, выполняющих работу с зарядами. В аккумуляторе происходит снижение электрического потенциала из-за внутреннего сопротивления. Потенциал уменьшается из-за внутреннего сопротивления \ (- Ir \), в результате чего напряжение на клеммах батареи равно \ ((\ epsilon — Ir) \).Затем напряжение уменьшается на ( IR ). Ток равен \ (I = \ frac {\ epsilon} {r + R} \).Ток через нагрузочный резистор равен \ (I = \ frac {\ epsilon} {r + R} \). Из этого выражения видно, что чем меньше внутреннее сопротивление r , тем больший ток подает источник напряжения на свою нагрузку R . По мере разряда батарей r увеличивается. Если r становится значительной частью сопротивления нагрузки, то ток значительно снижается, как показано в следующем примере.
Пример \ (\ PageIndex {1} \): анализ цепи с батареей и нагрузкой
Данная батарея имеет ЭДС 12,00 В и внутреннее сопротивление \ (0,100 \, \ Omega \). (a) Рассчитайте напряжение на его клеммах при подключении к нагрузке с \ (10.00 \, \ Omega \). (b) Какое напряжение на клеммах при подключении к нагрузке \ (0.500 \, \ Omega \)? (c) Какая мощность рассеивается при нагрузке \ (0.500 \, \ Omega \)? (d) Если внутреннее сопротивление увеличивается до \ (0.500 \, \ Omega \), найдите ток, напряжение на клеммах и мощность, рассеиваемую элементом \ (0.500 \, \ Omega \) загрузка.
Стратегия
Приведенный выше анализ дал выражение для тока с учетом внутреннего сопротивления. Как только ток будет найден, напряжение на клеммах можно рассчитать с помощью уравнения \ (V_ {terminal} = \ epsilon — Ir \). Как только ток будет найден, мы также сможем найти мощность, рассеиваемую резистором.
Решение
- Ввод заданных значений ЭДС, сопротивления нагрузки и внутреннего сопротивления в приведенное выше выражение дает \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {10.10 \, \ Omega} = 1.188 \, A. \] Введите известные значения в уравнение \ (V_ {terminal} = \ epsilon — Ir \), чтобы получить напряжение на клеммах: \ [V_ { клемма} = \ epsilon — Ir = 12.00 \, V — (1.188 \, A) (0.100 \, \ Omega) = 11.90 \, V. \] Напряжение на клеммах здесь лишь немного ниже, чем ЭДС, что означает, что ток втягивается этой легкой нагрузкой незначительно.
- Аналогично, при \ (R_ {load} = 0.500 \, \ Omega \) ток равен \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {0.2} {R} \) или \ (IV \), где В, — напряжение на клеммах (в данном случае 10,0 В).
- Здесь внутреннее сопротивление увеличилось, возможно, из-за разряда батареи, до точки, в которой оно равно сопротивлению нагрузки. Как и раньше, мы сначала находим ток, вводя известные значения в выражение, получая \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {1.00 \, \ Omega} = 12.00 \, A. \] Теперь напряжение на клеммах равно \ [V_ {terminal} = \ epsilon — Ir = 12.00 \, V — (12.2 (0.500 \, \ Omega) = 72.00 \, W. \] Мы видим, что повышенное внутреннее сопротивление значительно снизило напряжение на клеммах, ток и мощность, подаваемую на нагрузку.
Значение
Внутреннее сопротивление батареи может увеличиваться по многим причинам. Например, внутреннее сопротивление перезаряжаемой батареи увеличивается с увеличением количества раз, когда батарея перезаряжается. Повышенное внутреннее сопротивление может иметь двоякое влияние на аккумулятор.Сначала снизится напряжение на клеммах. Во-вторых, аккумулятор может перегреться из-за повышенной мощности, рассеиваемой внутренним сопротивлением.
Упражнение \ (\ PageIndex {1} \)
Если вы поместите провод прямо между двумя выводами батареи, эффективно закоротив клеммы, батарея начнет нагреваться. Как вы думаете, почему это происходит?
- Решение
Если к клеммам подсоединен провод, сопротивление нагрузки близко к нулю или, по крайней мере, значительно меньше внутреннего сопротивления батареи.2р) \). Мощность рассеивается в виде тепла.
Тестеры батарей
Тестеры батарей, такие как те, что показаны на рисунке \ (\ PageIndex {8} \), используют малые нагрузочные резисторы, чтобы намеренно потреблять ток, чтобы определить, падает ли потенциал клемм ниже допустимого уровня. Хотя трудно измерить внутреннее сопротивление батареи, тестеры батареи могут обеспечить измерение внутреннего сопротивления батареи. Если внутреннее сопротивление велико, батарея разряжена, о чем свидетельствует низкое напряжение на клеммах.
Рисунок \ (\ PageIndex {8} \): Тестеры батарей измеряют напряжение на клеммах под нагрузкой, чтобы определить состояние батареи. (a) Техник-электронщик ВМС США использует тестер аккумуляторов для проверки больших аккумуляторов на борту авианосца USS Nimitz . Тестер батарей, который она использует, имеет небольшое сопротивление, которое может рассеивать большое количество энергии. (b) Показанное небольшое устройство используется на небольших батареях и имеет цифровой дисплей для индикации допустимого напряжения на клеммах. (кредит А: модификация работы Джейсона А.Джонстон; кредит b: модификация работы Кейта Уильямсона)Некоторые батареи можно заряжать, пропуская через них ток в направлении, противоположном току, который они подают в прибор. Это обычно делается в автомобилях и батареях для небольших электроприборов и электронных устройств (Рисунок \ (\ PageIndex {9} \)). Выходное напряжение зарядного устройства должно быть больше, чем ЭДС аккумулятора, чтобы ток через него реверсировал. Это приводит к тому, что напряжение на клеммах батареи превышает ЭДС, поскольку \ (V = \ epsilon — Ir \) и I теперь отрицательны.
Рисунок \ (\ PageIndex {9} \): автомобильное зарядное устройство меняет нормальное направление тока через аккумулятор, обращая вспять его химическую реакцию и пополняя ее химический потенциал.Важно понимать последствия внутреннего сопротивления источников ЭДС, таких как батареи и солнечные элементы, но часто анализ цепей выполняется с помощью напряжения на клеммах батареи, как мы делали в предыдущих разделах. Напряжение на клеммах обозначается просто как В , без индекса «клемма».Это связано с тем, что внутреннее сопротивление батареи трудно измерить напрямую, и оно может со временем измениться.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Формула ЭДС — уравнения, решенные примеры и часто задаваемые вопросы
Электродвижущая сила — одно из важных понятий, которые помогают нам понять процесс электромагнетизма.Электродвижущая сила сокращенно называется ЭДС и тесно связана с более распространенным понятием напряжения. Электродвижущая сила — это полная энергия, обеспечиваемая батареей или элементом на кулон q заряда, проходящего через нее.
Величина ЭДС равна разности потенциалов на клеммах ячейки, когда нет тока, протекающего через данную электрическую цепь, и используемая формула известна как формула ЭДС. В этой статье мы подробно изучим формулу электродвижущей силы, идею физики ЭДС и, наконец, с помощью уравнения ЭДС с несколькими решенными примерами.
EMF Physics
Электродвижущая сила может быть определена как полное напряжение или разность потенциалов на клеммах батареи в разомкнутой цепи или, другими словами, когда через нее не течет ток. Это может не выглядеть так, поскольку это будет отличаться, но каждая батарея будет построена с определенным внутренним сопротивлением. Это связано с регулярным сопротивлением, которое уменьшает ток в электрической цепи, но оно заключено только внутри самой батареи.
Мы знаем, что когда цепь разомкнута, ток не будет течь через элемент, это означает, что внутреннее сопротивление батареи ничего не изменит, потому что нет тока, который мог бы уменьшить или замедлить. Таким образом, электродвижущую силу можно рассматривать как максимальную разность потенциалов или напряжение на двух выводах в идеализированном состоянии. Это объясняет физику ЭДС, и из этого мы можем понять, что электродвижущая сила — это частный случай разности напряжений.
Теперь возник вопрос, хотя электродвижущая сила вообще не является формой силы, тогда почему ее называют электродвижущей силой, в чем разница между ЭДС и регулярной разностью потенциалов, и что будет источник ЭДС? Чтобы ответить на эти сомнения, рассмотрим простую электрическую схему лампы, подключенной к батарее.
Мы знаем, что любое гальваническое устройство можно представить как двухполюсное устройство, которое поддерживает один вывод с более высоким потенциалом, а другой вывод — с более низким потенциалом.Более высокий электрический потенциал обычно известен как положительный полюс и обычно обозначается знаком плюс. Клемма с более низким потенциалом называется отрицательной клеммой и обозначается знаком минус. Это называется источником ЭДС.
Когда источник электродвижущей силы отключен от лампы, т. Е. Когда цепь разомкнута, то в данном источнике ЭДС нет чистого движения зарядов. После того, как цепь будет замкнута или повторно подключена к лампе, заряды будут перемещаться от одной клеммы батареи через лампу, что в дальнейшем приведет к тому, что лампа начнет светиться и вернется к другой клемме батареи.
Если мы рассмотрим обычный поток электрического тока, то есть положительный ток, положительные заряды имеют тенденцию покидать положительный вывод, проходить через лампу и попадать на отрицательный конец источника ЭДС. Так устроен источник ЭМП. В то же время электродвижущая сила батареи — это разность потенциалов, развиваемая на обоих концах данной батареи.
Следовательно, физика ЭДС объясняет, что электродвижущая сила — это полная энергия, поставляемая батареей или элементом на кулон заряда, проходящего через нее.Общая величина ЭДС равна напряжению или разности потенциалов на клеммах батареи, когда ток не проходит через данную электрическую цепь.
Уравнение ЭДС
Мы знаем, что заряды циркулируют в электрической цепи, для движения зарядов в данной электрической цепи нам необходимо приложить к ней внешнюю силу. Мы говорим, что внешний источник электричества, такой как батарея, использует такую силу, которая придает ускорение зарядам, и это называется электродвижущей силой.Несмотря на название, это не форма силы, а разность потенциалов, на самом деле, это особый случай разности потенциалов, который обычно обозначается символом.
Теперь давайте посмотрим на уравнение ЭДС:
Согласно определению физики ЭДС и ЭДС формула ЭДС имеет вид:
\ [\ Rightarrow EMF = \ varepsilon = \ frac {E} { Q} \]… .. (1)
Где,
E — Полная энергия батареи
Q — Полный заряд, протекающий через данную цепь
Уравнение (1) можно использовать, если мы знаем общую энергия батареи, используемой в цепи.Электродвижущая сила — это также разность потенциалов, возникающая в цепи, поэтому формулу ЭДС можно также найти с помощью закона Ома. Следовательно, мы пишем:
ε = IR… .. (2)
Где,
I — полный ток, протекающий в цепи
R — полное сопротивление, используемое в цепи
Поскольку мы знаем, что ЭДС зависит при внутреннем сопротивлении батареи мы должны заменить сопротивление суммой сопротивления и внутреннего сопротивления.Таким образом, уравнение (2) принимает следующий вид:
ε = I (r + R)
ε = Ir + IR
ε = V + Ir ……. (3)
Где,
V — Общая разность потенциалов в цепи
I — Полный ток, протекающий в цепи
r — Внутреннее сопротивление батареи
Следовательно, уравнение (1) и уравнение (3) известны как формула ЭДС или уравнение ЭДС. Давайте разберемся с формулой ЭДС и как найти ЭДС или как рассчитать ЭДС на нескольких решенных примерах.
Примеры:
1. Рассмотрим электрическую цепь с разностью потенциалов 5 В с током 1 А. Если внутреннее сопротивление используемой батареи составляет 0,8 Ом. Затем определите ЭДС цепи, используя формулу ЭДС.
Sol:
Дано,
Разность потенциалов электрической цепи = V = 5 вольт
Суммарный ток, протекающий по цепи = I = 1 A
Внутреннее сопротивление батареи = r = 0,8 Ом
Нас просят определить ЭДС цепи, используя уравнение ЭДС.Мы знаем, что ЭДС цепи можно рассчитать по формуле, приведенной ниже:
ε = V + Ir ……. (1)
Где,
V — Полная разность потенциалов, развиваемая в цепи
I — Суммарный ток, протекающий в цепи
r — Внутреннее сопротивление батареи
Подставляя значение разности потенциалов, тока и внутреннего сопротивления в уравнение (1), получаем:
ε = V + Ir
ε = 5 + (10,8)
ε = 5.8 Вольт
Следовательно, ЭДС схемы по формуле ЭДС составляет 5,8 Вольт.
2. Рассчитайте разность потенциалов на клеммах батареи, когда она подключена к нагрузке 10 Ом с ЭДС батареи, ε = 3 вольта и внутреннее сопротивление батареи 2 Ом.
Sol:
Дано,
Суммарная ЭДС батареи = ε = 3 вольта
Внешняя нагрузка, приложенная к батарее = R L = 10 Ом
Внутреннее сопротивление батареи = r = 2 Ом
Теперь нас просят определить разность потенциалов на клеммах аккумулятора.Перед этим рассчитаем ток, протекающий по данной цепи. согласно закону Ома мы знаем, что:
\ [\ Rightarrow I = \ frac {V} {R} = \ frac {\ varepsilon} {r + R_ {L}} \]…. (1)
I = 3/12 = 0,25 А
Теперь давайте определим разность потенциалов на клеммах аккумулятора. Формула ЭДС определяется следующим образом:
ε = V + Ir ……. (2)
Где,
V — полная разность потенциалов, развиваемая в цепи
I — полный ток, протекающий в цепи
r — Внутреннее сопротивление аккумулятора
Подставив значение ЭДС, тока и внутреннего сопротивления в уравнение (2), получим:
3 = V + (0.252)
В = 3 — 0,5
В = 2,5 В
Следовательно, разность потенциалов на клеммах аккумулятора составляет 2,5 В.
ЭДС и напряжение на клеммах
Когда вы забываете выключить автомобильные фары, они медленно тускнеют по мере разрядки аккумулятора. Почему они просто не мигают, когда батарея разряжена? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи. Причина снижения выходного напряжения для разряженных или перегруженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления.
Электродвижущая сила
Все источники напряжения создают разность потенциалов и могут подавать ток, если подключены к сопротивлению. В небольшом масштабе разность потенциалов создает электрическое поле, которое воздействует на заряды, вызывая ток. Мы называем эту разность потенциалов электродвижущей силой (сокращенно ЭДС). ЭДС — это вообще не сила; это особый тип разности потенциалов источника при отсутствии тока. Единицы измерения ЭДС — вольты.
Электродвижущая сила напрямую связана с источником разности потенциалов, например с конкретной комбинацией химических веществ в батарее.Однако при протекании тока ЭДС отличается от выходного напряжения устройства. Напряжение на выводах батареи, например, меньше, чем ЭДС, когда батарея подает ток, и оно падает дальше, когда батарея разряжается или разряжается. Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для сильно разряженной батареи).
Напряжение на клеммах
представляет собой схематическое изображение источника напряжения.Выходное напряжение устройства измеряется на его выводах и называется напряжением на выводах В . Напряжение на клеммах определяется уравнением:
Схематическое изображение источника напряжения
Любой источник напряжения (в данном случае сухой углерод-цинковый элемент) имеет ЭДС, связанную с источником разности потенциалов, и внутреннее сопротивление r, связанное с его конструкцией. (Обратите внимание, что сценарий E означает ЭДС.) Также показаны выходные клеммы, на которых измеряется напряжение на клеммах V.Поскольку V = ЭДС-Ir, напряжение на клеммах равно ЭДС, только если ток не течет.
$ V = ЭДС — Ir $,
где r — внутреннее сопротивление, а I — ток, протекающий во время измерения.
I — положительный, если ток течет от положительного вывода. Чем больше ток, тем меньше напряжение на клеммах. Точно так же верно, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.
ЭДС и внутреннее сопротивление
ЭДС и внутреннее сопротивлениеследующий: резисторы последовательно и Up: Electric Current (Электрический ток) Предыдущий: Сопротивление и удельное сопротивление Теперь настоящие батареи изготавливаются из материалов с ненулевым удельным сопротивлением.Отсюда следует, что настоящие батареи — это не просто источники чистого напряжения. Они также обладают внутренние сопротивления . Между прочим, чистое напряжение Источник обычно упоминается как ЭДС (что означает электродвижущая сила ). Конечно, ЭДС измеряется в вольтах. Батарею можно смоделировать как ЭДС, включенную последовательно с резистором. , который представляет собой его внутреннее сопротивление. Предположим, что такие батарея используется для управления током через внешний нагрузочный резистор, так как изображенный на рис.17. Обратите внимание, что на принципиальных схемах ЭДС представлена в виде двух близко расположенных параллельных линии неравной длины. Электрический потенциал более длинной линии больше, чем тот из более коротких по вольтам. Резистор представлен как зигзагообразная линия.
Рассмотрим батарею на рисунке.Напряжение аккумулятора равно
определяется как разница в электрическом потенциале между его положительным и
отрицательные клеммы: т.е. , точки и соответственно. Когда мы переходим от к
, электрический потенциал увеличивается на вольт, когда мы пересекаем
ЭДС, но затем уменьшается на вольт, когда мы пересекаем внутренний резистор.
Падение напряжения на резисторе следует из закона Ома, из которого следует, что
падение напряжения на резисторе, несущем ток
, находится в том направлении, в котором
текущие потоки.Таким образом, напряжение аккумулятора связано с его ЭДС.
и внутреннее сопротивление через
| (133) |
Обычно мы думаем, что ЭДС батареи по существу постоянная (поскольку она зависит только от химической реакции, происходящей внутри батареи, которая преобразует химическая энергия в электрическую), поэтому мы должны заключить, что напряжение батарея на самом деле уменьшается по мере увеличения тока, потребляемого от нее.Фактически, напряжение равно только ЭДС при пренебрежимо малом токе. Текущий розыгрыш от аккумулятора обычно не может превышать критическое значение
| (134) |
поскольку напряжение становится отрицательным (что может произойти только если резистор нагрузки также отрицательный: это практически невозможно). Отсюда следует, что если мы закоротим аккумулятор, подключив его положительные и отрицательные клеммы вместе с использованием проводящего провода с незначительным сопротивлением, ток, потребляемый от батареи, ограничен ее внутренним сопротивлением.Фактически в этом случае сила тока равна максимально возможной. Текущий .
Настоящая батарея обычно характеризуется его ЭДС (, т.е. , его напряжение при нулевом токе) и максимальный ток, который он может подавать. Например, стандартный сухой элемент ( т.е. , своего рода аккумулятор, используемый для питания калькуляторов и фонарей) обычно рассчитан на и скажи) . Таким образом, ничего действительно катастрофического не произойдет. произойдет, если мы закоротим сухой элемент.Мы разрядим батарею через сравнительно короткий промежуток времени, но опасно большой ток не будет поток. С другой стороны, автомобильный аккумулятор обычно рассчитывается на и что-то вроде (такой ток нужен для запустить стартер). Понятно, что автомобильный аккумулятор должен иметь много более низкое внутреннее сопротивление, чем у сухого элемента. Отсюда следует, что если мы были достаточно глупы, чтобы замкнуть автомобильный аккумулятор, в результате довольно катастрофически (представьте себе всю энергию, необходимую для запуска двигателя автомобиль собирается тонким проводом, соединяющим клеммы аккумулятора вместе).
следующий: резисторы последовательно и Up: Electric Current (Электрический ток) Предыдущий: Сопротивление и удельное сопротивление Ричард Фицпатрик 2007-07-14
Разница между напряжением и ЭДС?
Принципиальная разница между ЭДС и напряжением? Что такое напряжение?Необходимое количество энергии для перемещения единичного заряда из одной точки в другую известно как напряжение.Другими словами, напряжение определяется как разница между электрическими потенциалами. Он обозначается заглавной буквой «V» и измеряется в вольтах, обозначается буквой «V» и измеряется вольтметром.
- Один вольт — это разность электрического положения, равная одному амперу тока, который рассеивает один ватт мощности между двумя токопроводящими точками.
или
- Вольт — это разность потенциалов, которая перемещает один джоуль энергии на кулоновский заряд между двумя точками.
В = J / C = W / A… В вольт
Где:
- В = напряжение в вольтах
- Дж = Энергия в Джоулях
- C = заряд в Колумбусе
- Вт = выполненная работа в джоулях
- A = ток в амперах
ЭДС или электродвижущая сила — это подача энергии на заряд аккумуляторной батареей. Другими словами, ЭДС создает и поддерживает напряжение внутри активной ячейки и подает энергию в джоулях на каждую единицу кулоновского заряда.Он обозначается буквой «ε», а единица измерения такая же, как напряжение, то есть вольт.
ЭДС — максимальная разность потенциалов между двумя точками батареи при отсутствии тока от источника в случае разомкнутой цепи. Короче говоря, ЭДС является причиной, а напряжение или разность потенциалов — следствием.
E или ε = W / Q … в вольтах
Где:
- E или ε = энергия электродвижущей силы в вольтах
- Вт = выполненная работа в джоулях
- Q = Заряд в Колумбусе
Связанное сообщение: Разница между реальной землей и виртуальной землей
Таблица сравнения напряжения и ЭДС.| Характеристики | Напряжение | ЭДС |
| Представленный символ | В | E или ε |
| Определение | Напряжение — это разность потенциалов между двумя точками, по которой протекает ток. Это количество энергии на единицу заряда при перемещении между двумя точками. | ЭДС или электродвижущая сила — это количество энергии, подаваемой на заряд аккумуляторной батареей.Он вырабатывает напряжение внутри активных источников батареи и подает энергию в джоулях на каждый кулон заряда. |
| Выражение | Разница потенциалов или напряжение вызывает протекание тока между двумя точками. | ЭДС поддерживает разность потенциалов между двумя электродами. |
| Формулы | В = ИК Где В = напряжение в вольтах I = ток в амперах R = Сопротивление в Ом | E = I (R + r) E = W / Q Где: E или ε = ЭДС в вольтах Вт = выполненная энергия в Джоулях Q = Заряд в кулонах r = внутреннее сопротивление элемента батареи в Ом |
| Выполненные работы | Работа, выполняемая при перемещении заряда из одной точки в другую по проводнику. | В источнике действуют внешние силы, перемещающие заряд из одной точки в другую. |
| Источники | Электрическое поле и магнитное поле. | Активные устройства, такие как аккумуляторные элементы, солнечные элементы, трансформаторы, электрические генераторы и динамо-машины, фотодиоды и т. Д. |
| Интенсивность | Сила напряжения ниже ЭДС и непостоянна. | ЭМП имеет постоянную интенсивность с большей величиной. |
| Сопротивление | Напряжение зависит от сопротивления цепи. | ЭДС не зависит от сопротивления цепи. |
| Force Operation | Напряжение — это некулоновская операция. | ЭДС — это действие кулоновской силы. |
| Причина / следствие | Напряжение — это эффект ЭДС. | ЭДС является причиной напряжения. |
| Измерение | Напряжение можно измерить между любыми двумя точками. Его можно измерить с помощью вольтметра. | ЭДС можно измерить между концевыми выводами, когда через них не протекает ток.Его можно измерить с помощью измерителя ЭДС. |
Ниже приведены основные различия между напряжением и ЭДС.
- Название EMF на первый взгляд подразумевает, что это сила, которая заставляет ток течь. Но это неверно, потому что это не сила, а энергия, поставляемая для зарядки некоторым активным устройством, например, аккумулятором.
- ЭДС поддерживает разность потенциалов (P.D или напряжение), в то время как разность потенциалов вызывает протекание тока.
- Когда мы говорим, что ЭДС устройства (например, элемента) составляет 2 В, это означает, что устройство передает энергию в 2 джоуля на каждый кулон заряда. Когда мы говорим, что разность потенциалов между точками A и B цепи (предположим, что точка A имеет более высокий потенциал) составляет 2 В, это означает, что каждый кулон заряда будет отдавать энергию в 2 джоуля при перемещении из точки A в B.
Похожие сообщения:
Праймер EMF
Электромагнитные волны и поля
Электромагнитный Волны
Электромагнитные волны — это форма энергии, состоящая из вибрации. электрические и магнитные поля.Электрические поля создаются силами электрических зарядов, и магнитные поля создаются, когда электрические обвинения в движении. Когда прибор подключен к сети, электрическая вокруг прибора образуется поле; когда прибор включен горит и течет электрический ток, создается магнитное поле.
Обычный источники электромагнитного излучения
Основным естественным источником электромагнитного излучения является солнце.Естественный электромагнитная энергия (например, солнечный свет) необходима для фотосинтеза в растениях. Однако антропогенные источники составляют большую часть электромагнитного излучения. радиация в нашей окружающей среде. С распространением новых технологических устройств в нашем доме и на рабочем месте, мы все подвергаемся воздействию электромагнитных радиация ежедневно. Бытовые электроприборы, такие как фены, электрические печи, люминесцентные лампы, микроволновые печи, стереосистемы, мобильные телефоны, компьютеры и передатчики, поддерживающие эти элементы испускать электрические и магнитные поля различной интенсивности.
Измерение электромагнитных полей
Электрические и магнитные поля характеризуются длиной волны и частота. Длина волны — это расстояние, которое волна проходит за один цикл. колебания и измеряется в метрах. Частота измеряется числом циклов в секунду, а единицей измерения является Герцы (Гц). Один цикл в секунду равен одному герцу. Один килогерц (кГц) составляет 1000 Гц; один мегагерц (МГц) равен 1 миллиону Гц; один гигагерц (ГГц) составляет 1 миллиард Гц.Частота волны обратно пропорциональна ее частоте. длина по простой математической формуле: частота умноженная на длину волны = скорость света. Следовательно, чем выше частота, тем короче длина волны. При 50 Гц длины волн составляют 6000 км, а при 100 МГц они 3 метра. Электромагнитный спектр делится на ионизирующий. и неионизирующие полосы в зависимости от того, как волна взаимодействует с биологическими ткань. Ионизация заключается в удалении электронов из их нормального положения. в атомах и молекулах и может повредить ткани, в том числе генетический материал.Ионизирующая часть электромагнитного спектра состоит из ультрафиолетового света, гамма-лучи и рентгеновские лучи. У них очень короткие длины волн, очень высокие частоты и очень высокие интенсивности. Неионизирующая часть включает диапазон крайне низких частот (ELF), радиоволны и микроволны в диапазон радиочастот (RF) связи, а также инфракрасный и видимый свет. Радиоволны обычно определяются как волны в диапазоне 30 кГц. до 300 ГГц.Микроволны — это разновидность радиоволн.
Электромагнитный спектр
Другие термины, используемые при измерении ЭДС, показаны в таблице ниже.
Срок | Блок | Комментарий |
Частота | Гц (Гц) | Номер раз в секунду волна проходит свое максимальное значение |
Электрический Напряженность поля | Вольт / метр (В / м) | означает по «E» |
Магнитный Напряженность поля | Ампер / метр (А / м) | означает по «H» |
Магнитный Плотность потока | тесла (T) или Гаусс (G), где 10,000 G = 1T | обозначено по «Б» |
B = мкГн, где µ — магнитная проницаемость.
в низкие частоты, такие как частоты линий электропередачи, единицы магнитного потока чаще используются; поэтому магнитное поле обычно выражается в mG (миллиГаусс) или lT (микротесла) с 1 mG = 10 lT. Земля производит статическое магнитное поле, которое колеблется от 350 до 700 мГс, над поверхностью планеты, и который незначительно меняется в зависимости от дня и года ритмы. Существует также естественное электрическое поле, связанное с с различной разностью зарядов между землей и атмосферой.
в радиочастоты используемые измерения зависят от того, энергии удалено или близко к человеку, подвергающемуся воздействию. Плотность мощности составляет используется в ситуациях «дальнего поля», т.е. когда измерение взято на расстоянии более нескольких длин волн от источника РЧ. Дальнее поле источники включают телевизионные, радио и вышки сотовой связи и усики. Плотность мощности определяется как скорость потока энергии через заданная площадь поверхности.Он измеряется в ваттах на квадратный метр (Вт / м2, или в мВт / м² или / см²). Один мВт равен 0,001 Вт мощности и один мкВт равен 0,000001 Вт, так что 1 мВт / см = 1000 Вт / см или 10 Вт / м.
ближнего поля экспозиция, с другой стороны, — это экспозиция в непосредственной близости от Источник ЭМП. Примеры источников излучения ближнего поля для пользователя или потребительские, включают сотовые телефоны, радары и некоторые бытовые приборы. Для экспозиций в ближней зоне удельное поглощение Используется тариф (SAR).Он определяется как скорость поглощения энергии на единицу массы и выражается в Вт / кг. SAR измеряет, сколько Радиочастотная энергия поглощается телом. Измерение сложно, и обычно полученный из мер плотности мощности. SAR обсуждается в разделе под «беспроводными телефонами» Веб-сайт.
Далее
информация об электромагнитных полях:
Всемирная организация здравоохранения: www.who.int/peh-emf/
Федеральная комиссия по связи, Управление инженерии и технологий: Бюллетень OET 56, 4-е издание, август 1999 г. www.fcc.gov/oet/info/documents/bulletins/
ЭДС, подключение резисторов последовательно и параллельно — интерактивная практика
Поток электрического тока
Преобразование энергии на двух концах …
В электрической цепи всегда есть источник энергии и нагрузка . Первый генерирует энергию, а второй расходует ее. Источником может быть элемент, батарея, динамо-машина или даже солнечная батарея. Нагрузкой может быть резистор, лампочка, вентилятор или нагреватель. Мы знаем, что в то время как преобразования энергии происходят в источнике и в нагрузке, электрический ток течет по цепи от точки с более высоким потенциалом к точке с более низким потенциалом.
В приведенной выше анимации катящиеся шары имитируют электрический ток, опускаясь от точки с высокой потенциальной энергией к точке с низкой потенциальной энергией.Точно так же и ток, переходит от положительной клеммы — при более высоком потенциале — к отрицательной — при более низком потенциале. Однако, когда шары достигают ступней человека, они должны перейти от точки с более низкой потенциальной энергией к точке с более высокой потенциальной энергией. Это невозможно без вмешательство мужчины. Поэтому он наклоняется и поднимает их, чтобы они продолжали двигаться, превращая свою химическую энергию в потенциальную.
Когда заряды, переносящие электрический ток, достигают отрицательной клеммы ячейки, они сталкиваются с одним и тем же вызовом.Таким образом, химическая энергия в батарее превращается в электрическую, чтобы обеспечить заряды энергией для преодоления препятствий. Вот почему человек устает, а батарея разряжается через некоторое время, поскольку их соответствующие энергии превратились в разные формы.
Электродвижущая сила — ЭДС
Количество химической энергии, которое превратилось в электрическую энергию для перемещения + 1C по цепи, называется Электродвижущая сила клетки.
Единицы: Вольт
Мощность устройства
Энергия, потребляемая устройством за единицу времени, называется его мощностью.
Единицы:
P = E / t = J / t = Watts
Если напряжение равно V и заряд проходит через него Q за время t,
E = QV
Итак, P = QV / t = ItV / t = VI
P = VI
P = Вт; V = Вольт; Я = А
Мощность устройства должна быть указана вместе с напряжением, при котором она действительна.
60W, 240V означает, что мощность 60W вырабатывается при 240V.
Например, 1
Номиналы лампы 60 Вт, 240 В. Найдите его сопротивление.
P = VI
60 = 240I
I = 1/4 A
V = IR
240 = (1/4) R
R = 960 Ом.
Например, 2
Номиналы утюга — 1200Вт, 240В. Найдите ток и энергию, израсходованную за час.
P = VI
1200 = 240I
I = 5A.
E = Pt
E = 1200 X 3600
E = 4,32×10 6 J.
Например, 3
Номиналы лампы 60 Вт, 240 В. Из-за отключения электроэнергии напряжение падает до 200 В. Найдите новую мощность лампочки. Что бы вы заметили в лампочке?
P = VI
60 = 240I
I = 1/4 A
V = IR
240 = (1/4) R
R = 960Ω
При работе под новым напряжением
V = IR
200 = I x 960
I = 5/24 A
P = VI
P = 200 X 5/24
P = 41.7W
Лампа станет тусклее.
Доказательства наличия внутреннего сопротивления ячейки
Предположим, что заряд Q проходит по цепи за время t. ЭДС ячейки, внешнее сопротивление и ток равны E, R и I.
Энергия, производимая элементом = QE
Энергия, потребляемая внешним резистором = QV t
На практике было отмечено QV t
Таким образом, новое уравнение энергии принимает следующий вид:
QE = QV internal + QV external
Поскольку Q = It и V = IR => ItE = Irt + IRt
E = Ir + IR
E = I (r + R)
IR = E — Ir
Это разность потенциалов на внешнем резисторе (нагрузке). Поскольку вольтметр, подключенный к ячейке, показывает это, вместо ЭДС, он известен как Разница конечных потенциалов — В т .
Итак, В t = E — Ir
В разомкнутой цепи I = 0. Следовательно,
В t = E.
Например,
ЭДС ячейки составляет 12 В, а ее внутреннее сопротивление 2 Ом. Найдите ток и разность потенциалов на клеммах ячейки, если она подключена к внешнему резистору 4 Ом.
E = I (R + r)
12 = I (4 + 2)
I = 2A
V t = E — Ir
V t = 12 — 2×2 = 8
V t = 8V.
Подключение ячеек
Ячейки могут быть подключены последовательно, или параллельно, или их комбинация.
Последовательное соединение
Ячейки соединены таким образом, чтобы ток через каждую из них был одинаковым.
Параллельное подключение
Ячейки ЭДС соединены таким образом, что через каждую проходит равный ток.
Подключение резисторов
Резисторысерии
Если резисторы подключены таким образом, что ток через каждый из них одинаков, они считаются включенными последовательно.
Единственный резистор, который может заменить комбинацию, должен создавать напряжение V, когда ток через него равен I.
Для отдельных резисторов V = V 1 + V 2
V = IR 1 + IR 2
V = I (R 1 + R 2 )
Для эквивалентного резистора — заменитель,
V = IR T
IR T = I (R 1 + R 2 )
R T = (R 1 + R 2 )
Параллельные резисторы
Если резисторы подключены таким образом, что напряжение на них одинаково, они считаются параллельными.
Единственный резистор, который может заменить комбинацию, должен создавать напряжение V, когда ток через него равен I.
Для отдельных резисторов I = a + b
I = V / R 1 + V / R 2
V = V (1 / R 1 + 1 / R 2 )
Для эквивалентного резистора — заменитель,
I = V / R T
V / R T = V / (1 / R 1 + 1 / R 2 )
1 / R T = 1 / R 1 + 1 / R 2
E.g.1
Найдите полное сопротивление следующей цепи.
Общее сопротивление по xy:
1 / R T = (1/6) + (1/3)
1 / R T = (1 + 2) / 6 = 2/6 = 1/2
R T = 2 Ом
Общее сопротивление ветви = 2 + 4 = 6 Ом
Суммарное сопротивление трех ветвей, которые теперь параллельны
1 / R T = (1/6) + (1/15) + ( 1/10)
1 / R T = (5 + 2 + 3) / 30 = 10/30 = 1/3
R T = 3 Ом
E.g.2
Когда два резистора соединены последовательно, общее сопротивление составляет 25 Ом. Если они соединены параллельно, общее сопротивление составляет 6 Ом. Найдите сопротивление каждого.
Когда они включены последовательно,
R T = x + y = 25 Ом
Когда они подключены параллельно,
1 / R T = (1 / x) + (1 / y)
1 / R T = (x + y) / xy = 1/6
6 (x + y) = xy
6 X 25 = xy => xy = 150 => x = 150 / x
Итак, 150 / x + x = 25
x 2 + 150 = 25x
x 2 — 25x + 150 = 0
(x — 15) (x — 10) = 0
x = 15 или x = 10
Сопротивление каждого резистора составляет 15 Ом или 10 Ом
E.g.3
Найдите полное сопротивление следующей цепи и ток.
Так как все резисторы включены последовательно, общее сопротивление будет следующим:
R T = 1 + 2 + 3 + 4 = 10 Ом
Общий ток = 20/10 = 2A
Этот ток протекает через каждый резистор, как они есть. последовательно.
Например, 4
Найдите полное сопротивление следующей цепи и токи в каждой ветви.
Суммарное сопротивление по AB:
1 / R T = (1/6) + (1/3)
1 / R T = (1 + 2) / 6 = 2/6 = 1/2
R T = 2 Ом
Общее сопротивление цепи = 2 + 2 + 1 = 5 Ом
Общий ток = 15/5 = 3A
Этот ток делится на A обратно пропорционально сопротивлению каждой ветви — тем больше сопротивление , тем меньше ток, проходящий через него.
Поскольку два сопротивления параллельны,
6a = 3b
b = 2a
a + b = 3
3a = 3 => a = 1A; б = 2А.
Остальные резисторы получают ток 3А.
Дополнительные вопросы по резисторам в схемах
Найдите полное сопротивление следующих цепей:
Ответ: 5 Ом
Ответ: 6 Ом
Здесь вы можете попрактиковаться в расчетах с последовательным и параллельным подключением резисторов. Просто переместите ползунки и посмотрите, как изменится общее сопротивление.

 В
В А
А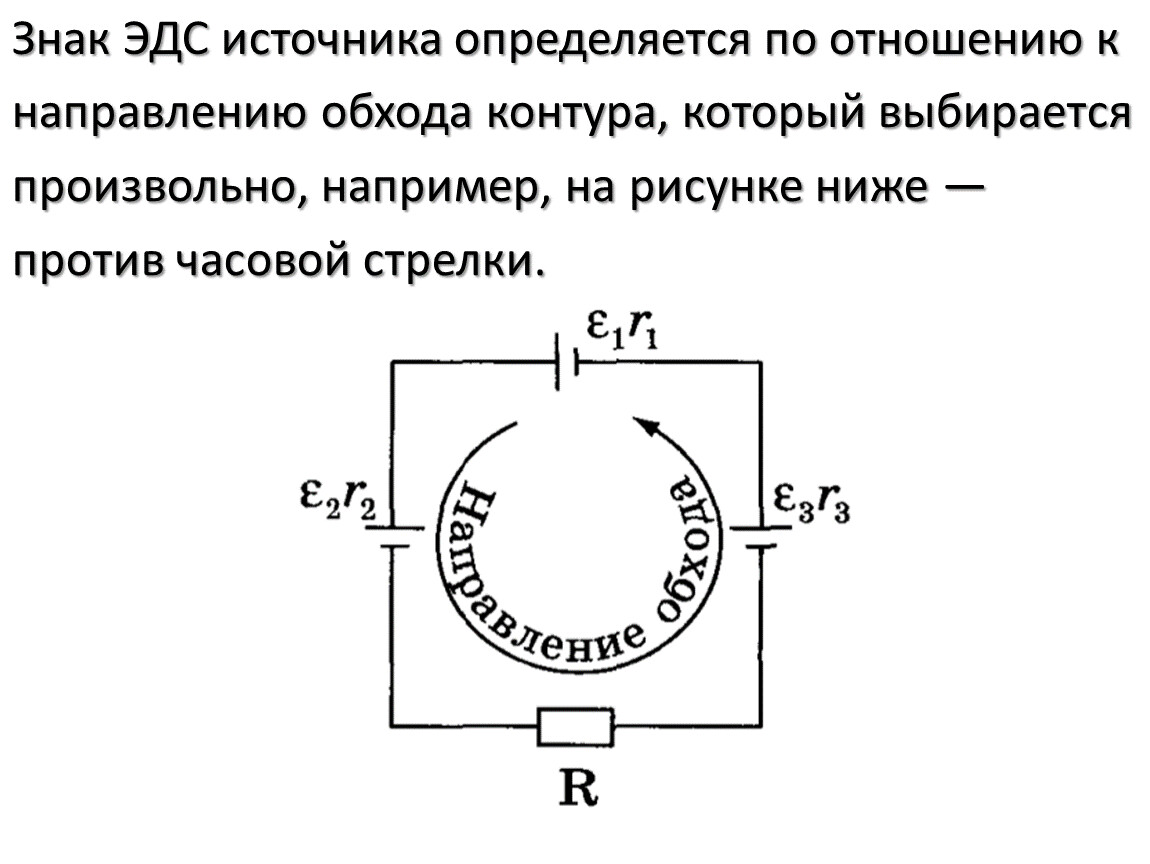 Е
Е B
B