Энергия магнитного поля

Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается источником тока на создание этого поля.

Рассмотрим цепь, содержащую катушку индуктивностью L и сопротивлением R_к, источник тока ε с внутренним сопротивлением r (рис. 125). Полное сопротивление цепи

R = R_к + r.

При замыкании цепи энергия источника тока расходуется на преодоление омического сопротивления и преодоление ЭДС самоиндукции ε_с, равной

ε_с= —

Здесь i – мгновенное значение силы тока, который при включении изменяется от 0 до I. Очевидно, что

или ε = iR – ε_c = iR + .

Умножим обе части равенства на

idt

εidt = i²Rdt +Lidi.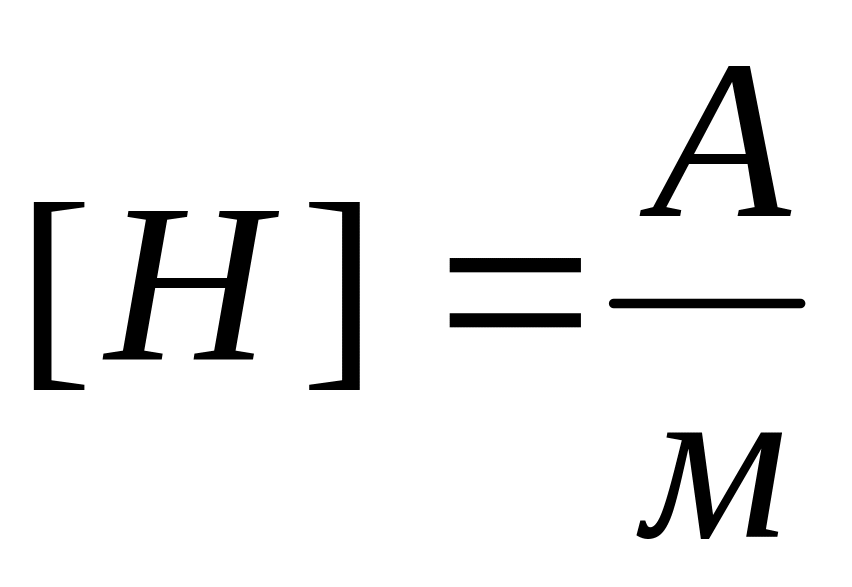

Здесь εidt – работа, совершаемая источником тока за время dt; Lidi – энергия, расходуемая на создание магнитного поля катушки, обладающей индуктивностью L, dW = Lidi; i²Rdt – энергия, расходуемая на нагревание проводника.

Полная энергия магнитного поля W, запасенная в катушке при нарастании тока от 0 до I будет

;

Если потокосцепление катушки Ψ = LI, то энергия магнитного поля будет

.

Выразим энергию магнитного поля через его характеристики В и Н.

Потокосцепление Ψ = NBS; напряженность поле в катушке Н = nI = , откуда . Тогда,

где V =Sl –объем катушки, в котором сосредоточено практически все магнитное поле, энергия которая равна .

Учитывая, что B = μ μ₀H, получим

.

Объемная плотность энергии магнитного поля — отношение энергии поля к объему ==.

Единица измерения Дж/ м³.

Магнитное поле в веществе.

Все вещества в той или иной мере обладают магнитными свойствами. Поэтому все вещества можно назвать магнетиками, т.е. веществами, способными приобретать во внешнем магнитном поле магнитные свойства, иначе говоря, намагничиваться и созда­вать собственное магнитное поле. Магнитные свойства вещества определяются магнитными свойствами электронов и атомов веще­ства.

Движение электрона в атоме по орбите радиуса r эквива­лентно некоторому замкнутому контуру с током. Магнитный момент ρ_m контура с током равен ρ_m = IS. Площадь кон­тура S = πr², а ток в нем I = e ν, где е – заряд электрона, ν – час­тота вращения электрона. Тогда ρ_m = IS = eνπr² . Если учесть, что скорость v вращения электрона v = 2 πrν, а

Величина ρ_m называется орбитальным магнитным моментом электрона.

Электрон, движущийся по орбите, обладает орбитальным механическим моментом импульса L = mvr.

Отношение орбиталь­ного магнитного ρ_m и механического L моментов

называют гиромагнитным отношением

Знак минус означает, что вектора ρ_m и L

противоположны по направлению (рис. 126).

Кроме орбитального электрон обладает собственными магнитным моментом ρ_ms и механическим L_s моментами, для которых гиро­магнитное отношение равно . Собственный механический мо­мент электрона называют

спином. Спин и связанный с ним собст­венный (спиновый) магнитный момент являются такими же неотъ­емлемыми свойствами электрона как его масса и заряд.

Магнитный момент атома слагается из орбитальных и соб­ственных моментов входящих в его состав электронов (а также ядра). При наложении внешнего магнитного поля напряженностью Н происходит определенная ориентация атомов и молекул веще­ства, что приводит к упорядоченному направлению векторов ρ_mi отдельных атомов и молекул магнетика, в результате чего объем ΔV магнетика приобретает определенный суммарный магнитный момент, который характеризуется вектором намагничивания J

,

где n –число атомов (молекул) в объеме ΔV. Единица измерения J [А/м ].

Число ориентированных молекул и степень их ориентации относи­тельно поля будут пропорциональны Н, т.е. J = χH, где χ – магнит­ная восприимчивость магнетика.

Магнитное поле в веществе создается двумя типами токов – макротоками и микротоками. Макротоки – это токи проводимости, образующиеся вследствие движения свободных зарядов. Микро­токи – это токи, обусловленные движением электронов в атомах, молекулах или ионах. При внесении магнетика во внешнее магнитное поле с ин­дукцией В₀ он намагничивается и создает собственное магнитное поле с индукцией

В‘. Индукция В результирующего поля после на­ложения внешнего и собственного полей будет равна В = В₀ + В‘. В зависимости от значения магнитной проницаемости μ все вещества разделяют на 3 группы: диамагнетики, парамагнетики и ферромагнетики.

Диамагнетики – это вещества, у которых μ < 1 и χ < 0. При наложении внешнего поля в них возникает собственное поле, на­правленное навстречу основному, т.е. векторы В₀ и В‘ имеют про­тивоположное направление. У диамагнетиков атомы вещества не обладают магнитным моментом (векторная сумма орбитальных и спиновых магнитных моментов электронов в атоме равна нулю). Однако при наложении на них внешнего магнитного поля в них на­водится некоторый магнитный момент, направленный навстречу внешнему полю, что и приводит к ослаблению внешнего магнит­ного поля в объеме диамагнетика.

Парамагнетики – это вещества, у которых суммарный маг­нитный момент атомов (векторная сумма орбитальных и спиновых магнитных моментов электронов в атоме) отличен от нуля. В таком веществе внешнее магнитное поле не только индуцирует магнит­ный момент, но и ориентирует магнитные моменты атомов по на­правлению поля несмотря на то, что тепловое движение стремится разбросать их равномерно по всем направлениям. Возникающий вследствии ориентации атомов положительный магнитный момент оказывается значительно больше, чем отрицательный момент (ин­дуцируемый вследствие прецессии электронов как у диамагнети­ков).

Поэтому результирующий магнитный момент оказывается по­ложительным, вещество ведет себя как парамагнетик, у которого μ > 1 и χ > 0.

Индукция В результирующего поля в парамагнетике будет выше, чем индукция внешнего поля В₀. В = В

0 + В’.

Намагничивание магнетика характеризуется вектором на­магничивания J, который имеет такую же размерность [А/м], что и напряженность Н. Поэтому для описания магнитного поля в магне­тиках часто пользуются выражением

Вектор намагничивания равен нулю в вакууме, а в веществе он пропорционален Н. J = χH и откуда

Безразмерная величина μ=1+χ называется относительной маг­нитной проницаемостью среды. Так как χ может быть положитель­ной и отрицательной, то μ может быть меньше единицы (у диамаг­нетиков) и больше единицы (у парамагнетиков).

Ферромагнетики – это особый класс веществ, намагничи­вание которых во много раз (до 10

6) превышает намагничивание диа-и парамагнетиков. К ним относятся Fe, Co, Gd и др., а также их сплавы и соединения. Ферромагнитные свойства присущи только кристаллам и объясняются их доменной структурой. В кристаллах возникают области, спонтанного (самопроизвольного) намагничивания – до­мены. В пределах домена ферромагнетик спонтанно намагничен до насыщения и обладает определенным магнитным моментом. На­правление этих моментов у различных доменов ориентированы произвольно, так что в отсутствие внешнего магнитного моля сум­марный магнитный момент всего тела равен нулю. При наложении внешнего магнитного поля (В

0) магнитные моменты доменов ори­ентируются по направлению внешнего магнитного поля, создавая собственное магнитное поле, индукция которого В’ на много больше В₀, а индук­ция суммарного поля В будет равна В=В’+В₀≃В’.

Для каждого ферромагнетика имеется определенная температура Т_с, называемая точкой Кюри, при значениях выше которой области спонтанного намагничивания (домены) распадаются, а вещество утрачивает ферромагнитные свойства. При температуре Т > Т_с ферромагнетик становится обычным парамагнетиком, магнитная восприимчивость которого χ подчиняется закону Кюри-Вейса

,

где с – постоянная Кюри.

Намагничивание J слабомагнитных диа-и парамагнетиков линейно зависит от напряженности Н внешнего поля. На рис. 127 показана зависимость J(H) для случая, когда J(0) = 0.

Намагничение достигает насыщения при некотором значении Н_нас для данного магнетика.

У ферромагнетиков сложная зависимость J(H) объясняется особенностью их доменной структуры. По мере нарастания напряженности внешнего магнитного поля увеличивается степень ориентации внешних моментов по направлению внешнего поля. При достижении Н = Н_нас векторы магнитных моментов всех доменов ориентированы параллельно полю и намагничение дости­гает насыщения. Для ферромагнетиков характерно наличие гисте­резиса. Увеличивая напряженность Н внешнего поля от Н = 0, можно довести намагничение до насыщения (точка 1 на рис. 128) при Н = Н_нас.

Если затем уменьшать напряженность Н, то намагничение будет изменяться по кривой 1-2 (а не по кривой 0-1 как при увеличении Н). В результате, когда напряженность внешнего поля Н станет равной нулю (точка 2), намагничение не исчезает и характеризуется величиной В_r, которая называется остаточной индукцией. При этом намагничение имеет значение J_r и называется остаточным намагничением. Намагничение обращается в нуль (точка 3) лишь под действием поля Н_с, имеющего направление противоположное вызвавшему намагниче­ние. Напряженность Н_с называется коэрцетивной силой. Существо­вание остаточного намагничения дает возможность изготовления постоянных магнитов.

Единица измерения вектора магнитной индукции

Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.

В — физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).

Магнитная индукция — векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:

Единица магнитной индукции. В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:

Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F_А = IBlsin a , а сила Лоренца действует на движущийся заряд:

где a — угол между векторами B и v .

Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила_м , постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:

В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,

Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.

Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.

Если напряженность электрического поля равна нулю, то сила Лоренца _л равна магнитной силе _м :

Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.

Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S — величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:

Ф=BScos

В СИ единица магнитного потока 1 Вебер (Вб) — магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:

Электромагнитная индукция-явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.

Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Опыты Фарадея показали, что сила индукционного тока I_i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром.

Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:

Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε_i.

По закону Ома для замкнутой цепи

Так как R не зависит от , то

ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:

Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:

Индуктивность контура L — коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.

Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.

Самоиндукция — явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.

Самоиндукция — частный случай электромагнитной индукции.

Индуктивность — величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.

Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :

Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.

ЭДС самоиндукции имеет в этом случае постоянное значение:

где I — начальное значение тока, t — промежуток времени, за который сила тока убывает от I до 0.

За время t в цепи проходит электрический заряд q = I_cpt . Так как I_cp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:

Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:

Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?

Энергия магнитного поля катушки W ₁ = LI ₁ 2 /2. По определению, индуктивность катушки L = Ф/I ₁. Следовательно,

Ответ: энергия поля равна 8,6 Дж; при уменьшении тока вдвое она уменьшится в 4 раза.

За положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора Такое исследование позволяет представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор направлен по касательной.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс) , в системе СИ — в теслах (Тл) , 1 тл = 10*4 гс. Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Вектор магнитной индукции (В) — это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.

Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:

где Мо — магнитная постоянная, R — расстояние, I — сила тока в проводнике.

Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.

Единица магнитной индукции — тесла (Тл).

Магнитная индукция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

В вакууме B = μ_H.

Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции.

Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.

Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника.

Рисунок – Правило буравчика

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.

Рисунок 3.2 – А) Образование магнитного потока в соленоиде

Б) Схема полей в соленоиде при протекании по обмотке переменного тока

Единица измерения В в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8464 — | 7349 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Тест по физике «Электромагнитная индукция».

Тест 11-1(электромагнитная индукция)

Вариант 1

1. Кто открыл явление электромагнитной индукции?

А. X. Эрстед. Б. Ш. Кулон. В. А. Вольта. Г. А. Ампер. Д. М. Фарадей. Е. Д. Максвелл.

2. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечисленных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке?

1. В катушку вставляется постоянный магнит.

2. Из катушки вынимается постоянный магнит.

3. Постоянный магнит вращается вокруг своей продоль­ной оси внутри катушки.

А. Только в случае 1. Б. Только в случае 2. В. Только в случае 3. Г. В случаях 1 и 2. Д. В случаях 1, 2 и 3.

3.Как называется физическая величина, равная произве­дению модуля В индукции магнитного поля на площадь S поверхности, пронизываемой магнитным полем, и косинус
угла а между вектором В индукции и нормалью п к этой поверхности?

А. Индуктивность. Б. Магнитный поток. В. Магнитная индукция. Г. Са­моиндукция. Д. Энергия магнитного поля.

4. Каким из приведенных ниже выражений определяется ЭДС индукции в замкнутом контуре?

A. Б. В. Г. Д.

5. При вдвигании полосового магнита в металлическое кольцо и выдвигании из него в кольце возникает индук­ционный ток. Этот ток создает магнитное поле. Каким по­люсом обращено магнитное поле тока в кольце к: 1) вдвигаемому северному полюсу магнита и 2) выдвигаемому се­верному полюсу магнита.

A. 1 — северным, 2 — северным. Б. 1 — южным, 2 — южным.

B. 1 — южным, 2 — северным. Г. 1 — северным, 2 — южным.

6. Как называется единица измерения магнитного потока?

А. Тесла. Б. Вебер. В. Гаусс. Г. Фарад. Д. Генри.

7. Единицей измерения какой физической величины является 1 Генри?

А. Индукции магнитного ноля. Б. Электроемкости. В. Самоиндук­ции. Г. Магнитного потока. Д. Индуктивности.

8. Каким выражением определяется связь магнитного по­ тока через контур с индуктивностью L контура и силой тока I в контуре?

A. LI. Б. . В. LI ^‘ . Г. LI². Д. .

9. Каким выражением определяется связь ЭДС самоин­дукции с силой тока в катушке?

А. Б. В. LI. Г. . Д. LI ^‘.

10. Ниже перечислены свойства различных полей. Какими из них обладает электростатическое поле?

1. Линии напряженности обязательно связаны с электри­ческими зарядами.

2. Линии напрялсенности не связаны с электрическими зарядами.

3. Поле обладает энергией.

4. Поле не обладает энергией.

5. Работа сил по перемещению электрического заряда по замкнутому пути может быть не равна нулю.

6. Работа сил по перемещению электрического заряда по любому замкнутому пути равна нулю.

А. 1, 4, 6. Б. 1, 3, 5. В. 1, 3, 6. Г. 2, 3, 5. Д. 2, 3, 6. Е. 2, 4, 6.

11. Контур площадью 1000 см² находится в однородном магнитном поле с индукцией 0,5 Тл, угол между вектором В индукции и нормалью к поверхности контура 60°. Ка­ков магнитный поток через контур?

А. 250 Вб. Б. 1000 Вб. В. 0,1 Вб. Г. 2,5 · 10^-2 Вб. Д. 2,5 Вб.

12. Какая сила тока в контуре индуктивностью 5 мГн создает магнитный поток 2 · 10^-2 Вб?

А. 4 мА. Б. 4 А. В. 250 А. Г. 250 мА. Д. 0,1 А. Е. 0,1 мА.

13. Магнитный поток через контур за 5 · 10^-2 с равномер­но уменьшился от 10 мВб до 0 мВб. Каково значение ЭДС в контуре в это время?

А. 5 · 10^-4 В. Б. 0,1 В. В. 0,2 В. Г. 0,4 В. Д. 1 В. Е. 2 В.

14. Каково значение энергии магнитного поля катушки индуктивностью 5 Гн при силе тока в ней 400 мА?

А. 2 Дж. Б. 1 Дж. В. 0,8 Дж. Г. 0,4 Дж. Д. 1000 Дж. Е. 4·10⁵ Дж.

15. Катушка, содержащая n витков провода, подключена к источнику постоянного тока с напряжением U на выходе. Каково максимальное значение ЭДС самоиндукции в катушке при увеличении напряжения на ее концах от 0 В до U В?

A, U В, Б. nU В. В. U/п В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.

16. Две одинаковые лампы включены в цепь источника постоянного тока, первая последовательно с резистором, вторая последовательно с катушкой. В какой из ламп (рис. 1) сила тока при замыкании ключа К достигнет мак­симального значения позже другой?

А. В первой. Б. Во второй. В. В первой и второй одновременно. Г. В пер­вой, если сопротивление резистора больше сопротивления катушки. Д. Во второй, если сопротивление катушки больше сопротивления резистора.

17. Катушка индуктивностью 2 Гн включена параллельно с резистором электрическим сопротивлением 900 Ом, сила тока в катушке 0,5 А, электрическое сопротивление ка­тушки 100 Ом. Какой электрический заряд протечет в цепи катушки и резистора при отключении их от источника тока (рис. 2)?

А. 4000 Кл. Б. 1000 Кл. В. 250 Кл. Г. 1 • 10 ^-2 Кл. Д. 1,1 • 10^-3 Кл. Е. 1 • 10^-3 Кл.

18. Самолет летит со скоростью 900 км/ч, модуль вертикальной составляющей вектора индукции магнитного поля Земли 4 • 10⁵ Тл. Какова разность потенциалов между концами крыльев самолета, если размах крыльев равен 50 м?

А. 1,8 В. Б. 0,9 В. В. 0,5 В. Г. 0,25 В.

19. Какой должна быть сила тока в обмотке якоря электромотора для того, чтобы на участок обмотки из 20 витков длиной 10 см, расположенный перпендикулярно век­тору индукции в магнитном поле с индукцией 1,5 Тл, действовала сила 120 Н?

А. 90 А. Б. 40 А. В. 0,9 А. Г. 0,4 А.

20. Какую силу нужно приложить к металлической пере­мычке для равномерного ее перемещения со скоростью 8 м/с по двум параллельным проводникам, располо­женным на расстоянии 25 см друг от друга в однородном магнитном поле с индукцией 2 Тл? Вектор индукции перпендикулярен плоскости, в которой расположены рельсы. Проводники замкнуты резистором с электрическим сопротивлением 2 Ом.

А. 10000 Н. Б. 400 Н. В. 200 Н. Г. 4 Н. Д. 2 Н. Е. 1 Н.

Вариант 2

1. Как называется явление возникновения электрического тока в замкнутом контуре при изменении магнитного по­тока через контур?

А. Электростатическая индукция. Б. Явление намагничивания. В. Сила Ампера. Г. Сила Лоренца. Д. Электролиз. Е. Электромагнитная индукция.

2. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечислен­ных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке?

1. В катушку вставляется постоянный магнит.

2. Катушка надевается на магнит.

3)Катушка вращается вокруг магнита, находящегося
внутри нее.

А.В случаях 1, 2 и 3. Б. В случаях 1 и 2. В. Только в случае 1. Г. Только в случае 2. Д. Только в случае 3.

3. Каким из приведенных ниже выражений определяется магнитный поток?

A. BScosα. Б. . В. qvBsinα. Г. qvBI. Д. IBlsina.

4. Что выражает следующее утверждение: ЭДС индукции в замкнутом контуре пропорциональна скорости измене­ния магнитного потока через поверхность, ограниченную контуром?

А. Закон электромагнитной индукции. Б. Правило Ленца. В. Закон Ома для полной цепи. Г. Явление самоиндукции. Д. Закон электролиза.

5. При вдвигании полосового магнита в металлическое кольцо и выдвигании из него в кольце возникает индук­ционный ток. Этот ток создает магнитное поле. Каким полюсом обращено магнитное поле тока в кольце к: 1) вдви­гаемому южному полюсу магнита и 2) выдвигаемому южному полюсу магнита.

A. 1 — северным, 2 — северным. Б. 1 — южным, 2 — южным.

B. 1 — южным, 2 — северным. Г. 1 — северным, 2 — южным.

6. Единицей измерения какой физической величины является 1 Вебер?

А. Индукции магнитного поля. Б. Электроемкости. В. Самоиндукции. Г. Магнитного потока. Д. Индуктивности.

7. Как называется единица измерения индуктивности?

А. Тесла. Б. Вебер. В. Гаусс. Г. Фарад. Д. Генри.

8. Каким выражением определяется связь энергии маг­нитного потока в контуре с индуктивностью L контура и силой тока I в контуре?

А. . Б. . В. LI², Г. LI ^‘ . Д. LI.

9.Какая физическая величина х определяется выражением х= для катушки из п витков.

А. ЭДС индукции. Б. Магнитный поток. В. Индуктивность. Г. ЭДС само­индукции. Д. Энергия магнитного поля. Е. Магнитная индукция.

10. Ниже перечислены свойства различных полей. Какими из них обладает вихревое индукционное электрическое поле?

1. Линии напряженности обязательно связаны с электри­ческими зарядами.

2. Линии напряженности не связаны с электрическими зарядами.

3. Поле обладает энергией.

4. Поле не обладает энергией.

5. Работа сил по перемещению электрического заряда по замкнутому пути может быть не равна нулю.

6. Работа сил по перемещению электрического заряда по любому замкнутому пути равна нулю.

А. 1, 4, 6. Б. 1, 3, 5. В. 1, 3, в. Г. 2, 3, 5. Д. 2, 3, 6. Е. 2, 4, 6.

11. Контур площадью 200 см² находится в однородном магнитном поле с индукцией 0,5 Тл, угол между вектором В индукции и нормалью к поверхности контура 60°. Ка­ков магнитный поток через контур?

А. 50 Вб. Б. 2 · 10^-2 Вб. В. 5 · 10^-3 Вб. Г. 200 Вб. Д. 5 Вб.

12. Ток 4 А создает в контуре магнитный поток 20 мВб. Какова индуктивность контура?

А. 5 Гн. Б. 5 мГн. В. 80 Гн. Г. 80 мГн. Д. 0,2 Гн. Е. 200 Гн.

13. Магнитный поток через контур за 0,5 с равномерно уменьшился от 10 мВб до 0 мВб. Каково значение ЭДС в контуре в это время?

А. 5 · 10^-3 В. Б. 5 В. В. 10 В. Г. 20 В. Д. 0,02 В. Е. 0,01 В.

14. Каково значение энергии магнитного поля катушки индуктивностью 500 мГн при силе тока в ней 4 А?

А. 2 Дж. Б. 1 Дж. В. 8 Дж. Г. 4 Дж. Д. 1000 Дж. Е. 4000 Дж.

15. Катушка, содержащая п витков провода, подключена к источнику постоянного тока с напряжением U на выхо­де. Каково максимальное значение ЭДС самоиндукции в катушке при уменьшении напряжения на ее концах от U В до 0 В?

A. U В. Б. nU В. В. U/n В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.

16. В электрической цепи, представленной на рисунке 1, четыре ключа 1, 2, 3 и 4 замкнуты. Размыкание какого из четырех даст лучшую возможность обнаружить явление самоиндукции?

А. 1. Б. 2. В. 3. Г. 4. Д. Любого из четырех.

17. Катушка индуктивностью 2 Гн включена параллельно с резистором электрическим сопротивлением 100 Ом, сила тока в катушке 0,5 А, электрическое сопротивление ка­тушки 900 Ом. Какой электрический заряд протечет в це­пи катушки и резистора при отключении их от источника тока (рис. 2)?

А. 4000 Кл. Б. 1000 Кл. В. 250 Кл. Г. 1 • 10^-2 Кл. Д. 1,1 • 10^-3 Кл. Е. 1 • 10^-3 Кл.

18. Самолет летит со скоростью 1800 км/ч, модуль вертикальной составляющей вектора индукции магнитного поля Земли 4 • 10^-5 Тл. Какова разность потенциалов между кон­цами крыльев самолета, если размах крыльев равен 25 м?

А. 1,8 В. В. 0,5 В. В. 0,9 В. Г. 0,25 В.

19. Прямоугольная рамка площадью S с током I помеще­на в магнитном поле с индукцией В . Чему равен момент силы, действующей на рамку, если угол между вектором В и нормалью к рамке равен а?

A. IBS sin а. Б. IBS. В. IBS cos а. Г. I²BS sin а. Д. I²BS cos а.

20. По двум вертикальным рельсам, верхние концы кото­рых замкнуты резистором электрическим сопротивлением R, начинает скользить проводящая перемычка массой т и длиной I. Система находится в магнитном поле. Вектор индукции перпендикулярен плоскости, в которой расположены рельсы. Найдите установившуюся скорость и движения перемычки. Сила трения пренебрежимо мала.

А. . В. В. . Г. . Д. .

Ответы:

Номер вопроса и ответ

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

Вариант 1

Д

Г

Б

Б

Г

Б

Д

А

Д

В

Г

Б

В

Г

А

Б

Е

В

Б

Е

Вариант 2

Е

Б

А

А

В

Г

Д

Б

А

Г

В

Б

Д

Г

Г

А

Е

Б

В

А

Энергия электрического и магнитного полей

В исследованиях электричества позиционно-зависимые векторы E , D , H и B используются для описания полей.

• E — напряженность электрического поля, с единицами измерения вольт на метр (В · м ⁻¹ ).
• D — диэлектрическое смещение, с единицей ампер-секунды на квадратный метр (А · м ⁻² ).
• H — напряженность магнитного поля, с единицами измерения ампер на метр (А · м ⁻¹ ).
• B — магнитная индукция, с единиц тесла (Т = В · м ⁻² ).

Плотность энергии (энергия на объем) обозначается w , и имеет единицы измерения В · м · м ⁻³ или Дж · м ⁻³ .
Это переводит энергию электрического поля, энергию магнитного поля и энергия электромагнитного поля до

Передача энергии поля также возможна без среды через пустое пространство.

Подача напряжения U на конденсатор емкостью C (Фарад [Ф] или A В ^-1 с) дает накопленную энергию электрического поля

Таким образом, конденсаторы можно использовать для хранения энергии, например, в велосипедных фарах. Суперконденсаторы (также известные как электрохимические двухслойные конденсаторы) показаны на рисунке справа. Их можно заряжать или разряжать в течение
в секунду. Для велосипедов есть примеры с U = 2.3 В,
C = 60 F, а вес 15 грамм. Исходя из этих данных, можно рассчитать плотность энергии около 3 Втч / кг из приведенных выше уравнений. Плотность энергии суперконденсаторов примерно на порядок ниже по сравнению с батареи. Однако время зарядки и разрядки аккумуляторов составляет примерно В 100 раз медленнее по сравнению с конденсаторами. Таким образом, удельная мощность конденсаторов составляет около на порядок лучше (3000 Вт / кг для примера здесь).

Суперконденсаторные поезда метро, ​​трамваи и автобусы, обеспечивающие регенерацию энергии торможения и возможность работать без проводов теперь используются в Китай. Суперконденсатор питает автомобили на расстояние более 2 км, а зарядка занимает 30 секунд на каждой станции через фиксированное питание.

Для энергии магнитного поля рассмотрим катушку с самоиндукцией L (единицы Генри [H] или V A ⁻¹ с) и через него протекает ток I .Запас энергии магнитного поля

Хранение энергии в магнитных полях дорогое удовольствие, что делает технические применения непрактичными. Например, большие сверхпроводящие магниты, охлаждаемые жидким гелием, для магнитно-резонансной томографии (МРТ) или Для спектроскопии ядерного магнитного резонанса (ЯМР) в сильном поле требуются токи 200 А. Собственная индуктивность в катушке 180 Гн дает приличную энергию магнитного поля около 1 кВтч. Однако магнит весит несколько сотен фунтов и стоит более миллиона долларов.Высокотемпературные сверхпроводники дают некоторую надежду на более дешевый метод хранения энергии в магнитных полях в будущем.

Электромагнитные поля используются не только для хранения энергии. Передатчики радиостанций с питанием мощностью 100 кВт может распределять передаваемую энергию на территорию диаметром 100 км. Сотовый телефон также использует энергию электромагнитного поля. Для телефона с номинальной мощностью 1 Вт При использовании телефона в час излучается около 1 кДж энергии.

Энергия в магнитном поле — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните, как можно накапливать энергию в магнитном поле
• Выведите уравнение для энергии, запасенной в коаксиальном кабеле, с учетом плотности магнитной энергии.

Энергия конденсатора хранится в электрическом поле между его пластинами. Точно так же индуктор может накапливать энергию, но в своем магнитном поле.Эту энергию можно найти, интегрировав плотность магнитной энергии,

больше соответствующего объема. Чтобы понять, откуда взялась эта формула, давайте рассмотрим длинный цилиндрический соленоид из предыдущего раздела. Снова используя приближение бесконечного соленоида, мы можем предположить, что магнитное поле по существу постоянное и задается везде внутри соленоида. Таким образом, энергия, запасенная в соленоиде, или плотность магнитной энергии, умноженная на объем, эквивалентна

При замене (Рисунок) это становится

Хотя это уравнение получено для частного случая, оно дает энергию, запасенную в магнитном поле любой индуктивности .Мы можем убедиться в этом, рассмотрев произвольную катушку индуктивности, через которую проходит изменяющийся ток. В любой момент величина наведенной ЭДС такова, что мощность, потребляемая катушкой индуктивности, равна

.

Полная энергия, запасенная в магнитном поле, когда ток увеличивается от 0 до 90 · 106 I в интервале времени от 0 до 90 · 106 t , может быть определена путем интегрирования этого выражения:

Самоиндуктивность коаксиального кабеля (рисунок) показывает две длинные концентрические цилиндрические оболочки радиусов и. Как обсуждалось в разделе «Емкость по емкости», эта конфигурация представляет собой упрощенное представление коаксиального кабеля.Емкость на единицу длины кабеля уже рассчитана. Теперь (а) определите магнитную энергию, запасенную на единицу длины коаксиального кабеля, и (б) используйте этот результат, чтобы найти самоиндуктивность на единицу длины кабеля.

(a) Коаксиальный кабель здесь представлен двумя полыми концентрическими цилиндрическими проводниками, по которым электрический ток течет в противоположных направлениях. (б) Магнитное поле между проводниками можно найти, применив закон Ампера к пунктирной траектории.(c) Цилиндрическая оболочка используется для определения магнитной энергии, запасенной на длине l кабеля.

Стратегия Магнитное поле внутри и снаружи коаксиального кабеля определяется законом Ампера. Основываясь на этом магнитном поле, мы можем использовать (рисунок) для расчета плотности энергии магнитного поля. Магнитная энергия рассчитывается как интеграл плотности магнитной энергии, умноженный на дифференциальный объем по цилиндрической оболочке. После того, как интегрирование выполнено, у нас есть закрытое решение для части (а).На основании этого результата и (рисунок) определяется самоиндукция на единицу длины.

Решение

1. Мы определяем магнитное поле между проводниками, применяя закон Ампера к пунктирной круговой траектории, показанной на (Рисунок) (b). Из-за цилиндрической симметрии постоянно вдоль пути, а
   

   
   Это дает нам
   

   
   В области за пределами кабеля аналогичное применение закона Ампера показывает, что, поскольку чистый ток не пересекает область, ограниченную круговой траекторией, этот аргумент также справедлив, когда это происходит в области внутри внутреннего цилиндра.Таким образом, вся магнитная энергия кабеля сохраняется между двумя проводниками. Поскольку плотность энергии магнитного поля составляет
   

   
   энергия, запасенная в цилиндрической оболочке с внутренним радиусом r , внешним радиусом и длиной l (см. Часть (c) рисунка) составляет
   

   
   Таким образом, полная энергия магнитного поля на длине л кабеля составляет
   

   
   , а энергия на единицу длины равна.

2. Из (рисунок),
   

   
   , где L — собственная индуктивность коаксиального кабеля длиной l .Приравнивая предыдущие два уравнения, находим, что самоиндукция на единицу длины кабеля составляет
   

Значение Индуктивность на единицу длины зависит только от внутреннего и внешнего радиусов, как видно из результата. Чтобы увеличить индуктивность, мы могли либо увеличить внешний радиус, либо уменьшить внутренний радиус. В пределе, когда два радиуса становятся равными, индуктивность стремится к нулю. В этом пределе нет коаксиального кабеля. Кроме того, магнитная энергия на единицу длины из части (а) пропорциональна квадрату тока.

Проверьте свое понимание Сколько энергии сохраняется в катушке индуктивности (рисунок) после того, как ток достигает максимального значения?

Сводка

• Энергия, запасенная в катушке индуктивности U , составляет
  
• Собственная индуктивность на единицу длины коаксиального кабеля составляет
  

Концептуальные вопросы

Шоу, у которого есть единицы энергии.

Проблемы

В данный момент ток 0.20 А протекает через катушку с проволокой, энергия, запасенная в ее магнитном поле, равна. Какова собственная индуктивность катушки?

Предположим, что прямоугольный тороид имеет 2000 обмоток и самоиндукцию 0,040 Гн. Если, то какой ток течет через прямоугольный тороид, когда энергия в его магнитном поле равна

Соленоид A плотно намотан, в то время как соленоид B имеет обмотки, равномерно распределенные с зазором, равным диаметру провода.В остальном соленоиды идентичны. Определите соотношение энергий, накопленных на единицу длины этих соленоидов, когда через каждый из них протекает одинаковый ток.

Катушка индуктивности 10 Гн проводит ток 20 А. Сколько льда может быть растоплено за счет энергии, накопленной в магнитном поле индуктора? ( Подсказка : используйте значение льда.)

Катушка с самоиндуктивностью 3,0 Гн и сопротивлением 1 м3 проводит постоянный ток 2,0 А. а) Какая энергия хранится в магнитном поле катушки? (б) Какая энергия в секунду рассеивается на сопротивлении катушки?

А ток 1.2 А протекает по коаксиальному кабелю, внешний радиус которого в пять раз превышает его внутренний радиус. Какая энергия магнитного поля хранится в кабеле длиной 3,0 м?

Глоссарий

Плотность магнитной энергии

энергия, запасенная на единицу объема в магнитном поле

Магнитная энергия | Магнит-Лексикон / Глоссарий

Каждое магнитное поле содержит энергию, также называемую магнитной энергией. В физике она постоянная. Поскольку магнитное поле создается электрическими токами, магнитная энергия является формой энергии движущихся носителей заряда (электронов).Чтобы понять, откуда берется эта энергия, стоит взглянуть на то, как работает магнитное поле.

Как создается магнитное поле?

Магнетизм описывается магнитными полями. Это вызвано магнитными материалами (например, постоянными магнитами), электрическим током (например, токонесущими катушками) или временным изменением электрического поля. Силовые линии магнитного поля указывают магнитный поток. Как и в случае с магнитным полем Земли, магниты (например, стержневые магниты) имеют северный и южный полюса, причем первый всегда совмещен в направлении арктического магнитного полюса.Поскольку работа выполняется для создания магнитного поля, это поле имеет энергию в накопителе магнитной энергии.

В зависимости от материала количество магнитной энергии может быть разным. Гистерезис описывает эту связь. Опять же, эти эффекты описываются уравнениями Максвелла, которые показывают, почему носители электрического заряда генерируют магнитные поля.

Как можно рассчитать магнитную энергию?

Чтобы описать энергию магнитного поля (катушки), можно составить формулу для магнитной энергии.Единица плотности магнитной энергии в любой точке магнитного поля в вакууме (полная энергия: E), необходимы следующие единицы и размеры:

• (напряженность магнитного поля, система CGS: единица Эрстеда)
• (плотность магнитного потока в точке, единица Тесла)
• Л (индуктивность магнитной энергии катушки, ед. Генри)
• I (сила тока, единица ампер)

Это приводит к:

соответственно. на общую энергию:

Правило: чем выше магнитная энергия, тем больше магнитные силы.

Применение магнитной энергии

Когда кусок железа приближается к магниту, в воздушном пространстве между ними создается энергия, превышающая энергию магнитного объекта. В зависимости от проницаемости железа доля этой энергии уменьшается. Но когда магнит и железо касаются друг друга, энергия поля полностью исчезает в воздушном пространстве.

Магнит должен немного поработать, чтобы надеть его, но он снижает собственную магнитную энергию. Интересно то, что магнитное поле магнита не разрушается, а перемещается каждый раз, когда снова необходимо приложить внешнюю силу, чтобы отделить железо от магнита.Затем магнитная энергия в бегающем сне также снова увеличивается.

Классическим примером использования магнитной энергии является генератор. Проще говоря, магнит внутри катушки постоянно вращается по кругу, а магнитное поле выполняет свою работу. Вот сила Лоренца, действующая на движущиеся электрические заряды в магнитном поле. В результате может генерироваться ток и индуцироваться напряжение при изменении магнитного поля.

Физика для науки и техники II

из отдела академических технологий на Vimeo.

9,9 Энергия, запасенная в магнитном поле, и плотность энергии

Чтобы вычислить энергию, запасенную в магнитном поле индуктора, давайте вспомним уравнение контура LR цепи. В этой схеме, если мы рассмотрим нарастание фазы тока, у нас есть резистор и катушка индуктивности, соединенные последовательно, и как только мы включим переключатель, ток i будет выходить из источника питания, проходить через резистор R и через катушку индуктивности L от положительной клеммы к отрицательной клемме источника питания.Выбрав для обхода цепи по часовой стрелке, мы выразили соответствующее уравнение контура как ε минус i умноженное на R минус L умноженное на di на dt равно 0.

Это произошло из-за того, что, когда мы пересекаем резистор в направлении протекания тока, потенциал уменьшается в -1 раз R . И во время нарастания тока, когда ток нарастает от 0 до –, мы собираемся закончить с самоиндуцированной ЭДС, и это проявится так, что будет противодействовать своей причине.Поэтому он будет пытаться генерировать ток в направлении, противоположном направлению потока этого исходного тока. Следовательно, мы будем пересекать ЭДС в направлении, противоположном направлению стрелки ЭДС, когда мы проходим через этот индуктор. Следовательно, мы имеем — L di более dt , и это была часть самоиндуцированной ЭДС.

Давайте продолжим и умножим обе части этого уравнения на текущее значение i . Умножьте обе стороны на текущее i .Если мы это сделаем, у нас будет ε i минус i 2 r минус Li di over dt равно 0. Давайте изменим это выражение, оставив ε умножить на i. слева и переместите остальные члены в правую часть. Следовательно, у нас будет i 2 R плюс Li di поверх dt с правой стороны.

Давайте попробуем интерпретировать каждый из этих членов в этом уравнении.Как вы помните, электродвижущая сила — это не что иное, как зарядный насос. Он просто перекачивает заряды с низким электрическим потенциалом в область с высоким электрическим потенциалом, и при этом он также выполняет определенную работу. Если он прокачивает q кулонов заряда через ε вольт разности потенциалов, то это составляет ε умноженное на q работы, выполненной на q местом расположения ЭДС. Это, конечно, происходит непосредственно из определения электрического потенциала.Электрический потенциал — это работа, совершаемая на единицу заряда.

Хорошо, если мы возьмем производную от этой величины, то у нас будет ε, умноженное на dq , на dt , что будет равно ε , умноженное на i , поскольку dq на dt — это i , и это в основном скорость работы, выполненной на q на ε , но скорость выполненной работы — это не что иное, как мощность. Другими словами, εi — это скорость, с которой источник электродвижущей силы, ЭДС, передает энергию в цепь.Другими словами, электродвижущая сила передает в цепь ε , умноженное на i энергии, каждую секунду. Это также эквивалентно, следовательно, подаваемой мощности.

Итак, второй член здесь, поэтому εi — это подаваемая мощность, а первый член фактически справа, i 2 R , — это то, что мы уже знакомы, и это скорость какая энергия появляется в резисторе как тепловая энергия. Скорость, с которой энергия проявляется как тепловая энергия в резисторе.Другими словами, это не что иное, как мощность, рассеиваемая через резистор.

Хорошо, опять же, если вы теперь вернетесь к нашему уравнению, ε умножить на i — это мощность, передаваемая электродвижущей силой в цепь. Другими словами, энергия, подводимая к контуру в единицу времени. Часть этой энергии в единицу времени рассеивается через резистор. Следовательно, эта большая часть мощности рассеивается из этой подаваемой мощности. Таким образом, мы заключаем, что остальная мощность идет на катушку индуктивности.Другими словами, последний член в правой части дает нам скорость, с которой энергия сохраняется в магнитном поле индуктора.

Таким образом, мы можем сказать, что Li di по сравнению с dt не что иное, как dU B по сравнению с dt , что является скоростью магнитного поля, хранящейся в магнитном поле индуктора, или это скорость при котором энергия хранится в магнитном поле индуктора. Итак, dU B over dt равно Li di over dt .Отсюда мы можем отменить dt ‘s, так что dU B будет равно Li , умноженному на di . Если мы проинтегрируем обе стороны, то в конечном итоге мы получим полную энергию, запасенную в магнитном поле индуктора, и она будет равна — и снова будет постоянной. Мы можем вынести это за пределы интеграла. И интеграл от i di даст нам i 2 больше 2. Таким образом, магнитная энергия индуктора будет равна половине L , умноженной на индуктивность, умноженную на квадрат тока, протекающего через этот индуктор. .

Итак, снова с помощью индукторов, мы можем генерировать пакеты магнитного поля, аналогичные случаю конденсаторов, которые позволяют нам генерировать или производить пакеты электрического поля. Опять же, как и в этом случае, мы можем хранить энергию в магнитных полях индуктора, и эта энергия будет равна половине индуктивности индуктора, умноженной на квадрат тока, протекающего через индуктор.

Здесь давайте вспомним корпус конденсатора и скажем, что вспомним, что энергия, запасенная в электрическом поле конденсатора, была равна U E , и это было q 2 по сравнению с 2 C .

Мы определили понятие плотности энергии ранее, и здесь мы также можем определить плотность энергии, связанную с магнитным полем, плотность энергии. Для этого давайте рассмотрим соленоид и предположим, что l представляет длину соленоида, а A представляет площадь поперечного сечения соленоида. Следовательно, A умноженное на l будет представлять объем соленоида.

Итак, мы рассматриваем соленоид.Скажем, у него круглое поперечное сечение примерно так, длина l , а затем площадь поперечного сечения A , и у нас есть связанные с ним витки, что-то вроде этого. Что ж, давайте обозначим плотность энергии с помощью малых u B , то есть по определению общую энергию индуктора, деленную на общий объем индуктора. В нашем конкретном случае это будет равно U B , разделенному на площадь поперечного сечения соленоида, умноженную на его длину, что даст нам объем этого соленоида, объем, через который магнитное поле заполнится, когда определенный ток и протекает через соленоид.

Хорошо, поскольку полная магнитная энергия, запасенная в магнитном поле индуктора, равна половине L , индуктивность, умноженная на квадрат тока, протекающего через индуктор, и для индуктивности соленоида была равна μ 0 n 2 умножить на l умножить на A и n 2 — это плотность числа витков, как вы помните, и, опять же, l — длина. Итак, мы можем выразить плотность энергии в явном виде.Что касается U B , у нас будет половина, а индуктивность будет μ 0 n 2 l умножить на A умножить на i 2 и разделить на объем, который равно A умножить на l .

Здесь длина сокращается в числителе и знаменателе, а площадь поперечного сечения соленоида сокращается в числителе и знаменателе. В итоге плотность энергии соленоида будет равна половине μ 0 n 2 умножить на i 2.Но если вы вспомните, что магнитное поле соленоида было μ 0 n , умноженное на i, и, как вы помните, это была постоянная величина, и она не менялась от точки к точке внутри соленоида.

Итак, чтобы получить здесь аналогичный тип выражения, давайте умножим оба числителя на μ 0 и разделим его на μ 0 . При этом в знаменателе будет половина 2 μ 0 , и умножив числитель на mu, мы получим μ 0 2 n 2 i 2, и это количество не что иное, как B 2.Таким образом, плотность энергии будет равна B 2 более чем в 2 раза выше проницаемости свободного пространства, и это выражение дает нам плотность магнитной энергии.

И снова, вы можете вспомнить плотность электрической энергии, которая представляет собой энергию на единицу объема для конденсатора, и которая была равна u E равно, была равна половине ε 0 умноженному на квадрат электрическое поле. И снова мы видим интересную параллель между магнитным полем и случаем электрического поля.

Из лаборатории Теслы в Лос-Аламос: мощные магниты совершают полный оборот

На этой неделе на сайте Energy.gov мы возвращаемся к легендарному соперничеству между двумя наиболее известными в истории изобретателями и инженерами в области энергетики: Томасом Эдисоном и Николя Тесла. Проверяйте каждый день, чтобы узнать больше об их жизни, их изобретениях и о том, как их вклад все еще влияет на то, как мы используем энергию сегодня. Поддержите своего фаворита с помощью хэштегов #teamedison и #teamtesla в социальных сетях или проголосуйте на нашем сайте.

В марте 2012 года ученые из Лос-Аламосской национальной лаборатории установили мировой рекорд, достигнув магнитного импульса 100,75 тесла, что примерно в 2 000 000 раз мощнее магнитного поля Земли.

Установка импульсного поля в Национальной лаборатории Лос-Аламоса включает в себя батареи конденсаторов, генераторы и технические системы, необходимые для поддержки множества мощных магнитов. Один из них — многозарядный магнит 100 тесла, который создает самое мощное неразрушающее магнитное поле в мире.

Изучение магнитов и их свойств неразрывно связано с одним из наших изобретателей на этой неделе: Николя Тесла. Тесла открыл вращающееся магнитное поле в 1882 году, физический принцип, который заметно фигурировал во многих его будущих изобретениях. Тесла (Тл) была удостоена чести очень немногих ученых. Она была обозначена как единица измерения плотности магнитного потока или силы магнитного поля в 1956 году. Тесла используется как единица измерения очень сильных магнитных полей. и является стандартом Международной системы единиц (СИ), а гаусс (Г) обычно используется для более слабых магнитных полей.Единица измерения определяется масштабом: одна тесла равна 10 000 гаусс. Для сравнения: магнитное поле Земли имеет плотность магнитного потока около 50 микротесла, или 0,00005 тесла.

Этот многозарядный магнит мощностью 100 тесла, названный так потому, что его можно использовать снова и снова, не разрушаясь силой создаваемого магнитного поля, является импульсным — это означает, что поле, которое он генерирует, может поддерживаться только на короткое время. промежуток времени. Сам магнит расположен внутри контейнера с жидким азотом, что поддерживает температуру -198.15 градусов по Цельсию (-324,67 градусов по Фаренгейту), что предотвращает перегрев магнита из-за мощного импульса электричества. Устройство импульсного поля и его набор магнитов доступны для использования исследователями и учеными из академических кругов и частного сектора в качестве назначенного пользователя.

Магнит 100 тесла в Национальной лаборатории Лос-Аламоса используется для изучения сверхпроводимости, того, как различные материалы ведут себя под воздействием очень сильного магнитного поля, и его даже можно использовать в качестве наномасштабного микроскопа.Все это стало возможным благодаря новаторским открытиям, сделанным Никола Тесла более века назад.

От [Вольт / метр] до [Тесла] и обратно

От [Вольт / метр] до [Тесла] и обратно

… от [Вольт / метр] до исторических [Тесла] и обратно.

Напомним введение электрического поля E из измерения электростатической силы F на заряде q. Эти понятия связаны соотношением F = q E где E = kq r / r ³ .Здесь сила F часто в [Ньютонах] ≡ [кг м / с ² ], электрический заряд q в [Кулоны], а электрическое поле E в [Ньютон / Кулон] ≡ [Вольт / метр] = [Франклин?].

Конечное значение «скорости света» c в относительность требует, чтобы любая сила между объекты зависят от рамки наблюдения, так что, например, нейтральный токоведущий провод не будет нейтральным по отношению к движущемуся плата. То есть движущийся заряд испытывает кулоновскую силу.Отсюда магнетизм. Если мы определим плату вектор ¹ q _m движущегося заряда или текущий элемент в [Кулонах] как q _м = q v / c = I δs / c, тогда можно определить вектор магнитного поля в единицах электрического поля (например, [N / C]) как B ‘= k q _м × r / r ³ . Для изолированного заряда q это выражение работает только для малых скоростей в отсутствие ускорения, но для установившихся токов в замкнутый цикл выражение является робастным.Это поле в свою очередь оказывает силу Лоренца на отдельно движущийся заряд или ток q _м равно F = q _м × B ‘. Величина q _м — это эффективный дефицит заряда , видимый нами. поскольку сопутствующие заряды увеличивают свою скорость ² , в то время как величина B ‘- это сила, действующая на вектор заряда, перпендикулярный B ‘, на единицу q _м .

Таким образом магнитный взаимодействия могут быть полностью выражены с использованием только постоянной Кулона k, ваш любимый блок для электрического заряда и знакомый механический единиц силы, расстояния и т. д. Таким образом, магнитное поле можно рассматривать как электрические поля, которые вызваны и действуют зарядовые векторы вместо зарядов . Форма уравнений для магнитные поля и силы зеркально отражают электростатические (см. рисунок справа), с учетом сил между векторами зарядов q _m отдельно от сил между скалярными зарядами q.Роль силовой закон в каждом уравнении легко увидеть. Электрические и магнитные выражения для энергии поля U на единицу объема V также хорошо сочетаются друг с другом, то есть U / V = ​​(E ² + B ‘ ² ) / 8πk, как и выражения для скалярного и векторного потенциала (последний абзац ниже).

Два разных определения вместо этого использовал ³ в Système International d’Unités (SI), возможно, потому что магнетизм, электростатика, и свет сначала рассматривались как отдельные явления.Особенно, вектор заряда q _m ‘движущегося заряда или текущий элемент определяется как q _м ‘= q v = I δs = q _м c в единицах [Кулон м / с] ≡ [Амперметр], т. е. как упомянутый выше дефицит начислений, умноженный на c. это Естественно тогда определить магнитную индукцию как B = B ‘/ c в [Ns / Cm] ≡ [Tesla], т.е. как усилие на единицу q _м ‘.Это дает начало формам Био-Савара. B = (k / c ² ) q _м ‘× r / r ³ и Lorentz F = q _m ‘× B , используемых в большинстве тексты. Две вариации на постоянной Кулона также определены, чтобы помочь в определение невакуумных полей, а именно ε _o À1 / (4πk) и μ _o À4πk / c ² .

Чтобы узнать, предлагает ли B ‘ дополнительная точка зрения, попробуйте ответить на эти вопросы.Какая напряженность магнитного поля B ‘в [Вольт / метр] рекордного 14,7 Магнитное поле Теслы? Как это по сравнению с 30 [кВ / см] напряженность поля, которую часто называют величиной ионизационного пробоя для сухого воздуха? Почему ионизация менее важна в присутствии этого магнитного поля?

Также небольшое предостережение: Тот факт, что « q _m1 × ( q _m2 × k r / r ³ ) не всегда равно — q _m2 × ( q _m1 × k r / r ³ ) » поднимает флаг с уравнениями выше в контексте действие-противодействие и сохранение импульса.Если это интегрировано по замкнутой токовой петле несоответствие исчезает. В процессе, однако это наблюдение подчеркивает недостаток того, что мы говорим студенты-интро-физики, игнорируя (например, в выражении E-поля выше) наведенная составляющая электрического поля (например, соответствующие к рельсовым пушкам) выражается как производная по времени (-δ A / δt) векторного потенциала (электрокинетический импульс Максвелла на единицу заряда) A = (k / c ² ) q _m ‘/ r = A ‘ / c.Как вы можете себе представить, A ‘= k q _m / r подобен скалярному потенциалу Φ = kq / r также в [Вольтах]. Однако в большинстве вводных текстов избегается векторный потенциал. Уменьшаются ли последствия этого упущения, если утверждать, что Уравнение Лоренца без индуцированного электрического поля работает для внешнего статическое магнитное поле (например, как от фиксированной токовой петли), но не для изменяющихся во времени полей (например, как поле движущегося заряда)? Эти предостережения могут быть еще одной причиной того, что Био-Савар обычно вводят. с I δs , но не q v .

---

Сноски:

[1] Величина вектора заряда вокруг петли также используется в промышленность по производству магнитов для измерения местной силы магнитного полюса. Учитывая это, какова сила [кулонов] типичного холодильника? магнит?

[2] Перпендикуляр составляющая силы между двумя объектами, движущимися с постоянной скоростью равно (объект-рамка) Собственная сила ⁴ раз Sqrt [1- (v / c) ² ], как показано на рисунке справа, где показано, как кажущаяся сила (d p / dt) и масса, умноженная на ускорение ( м м), отклоняться от действующей силы на движущийся объект.Для кулоновской силы перпендикулярно направлению движения равномерно движущихся зарядов, это дает F _⊥ = Sqrt [1- (v / c) ² ] kq ₁ q ₂ r _⊥ / r ³ . Второй фактор Sqrt [1- (v / c) ² ] вступает в игру для заряда, перемещающегося вместе с токовые элементы в постоянно движущемся проводе, чтобы он оставался нейтральным перед лицом сокращения длины по мере ускорения элемента. Наблюдаемая сила (перпендикулярная скорости) между движущимся заряд и попутно движущиеся токовые элементы в нейтральном проводе, таким образом, правильная сила, умноженная на 1- (v / c) ² .Следовательно, чистая сила между заряженным токовым элементом I δs и сопутствующим заряд q v можно рассматривать как правильную силу минус «чувствительный к скорости Кулоновская (или магнитная) сила между двумя зарядами, где qv / c и Iδs / c — величины задействованных дефицитных платежей. в магнитном взаимодействии. В нулевом проводе, конечно, что собственное усилие отменяется дополнительным неподвижным элементы заряда, оставляя для рассмотрения только магнитные взаимодействия.В перекрестные произведения в приведенных выше уравнениях учитывают тот факт, что каждое начисление дефицита воздействует на только на ту составляющую силы, перпендикулярную его векторное направление. Таким образом, вместо того, чтобы выбросить Био-Савара из синий для студентов-интрофизиков, релятивистская фрейм-зависимость силы могут быть использованы для объясните, почему и как взаимодействуют токи в нейтральных проводах друг с другом, но не со скалярными зарядами, в том числе (из их дефицитный характер) почему притягиваются параллельные токи.

[3] Сказанное выше предполагает, что модифицированный набор SI единиц, для которых E / B безразмерно, как и для Используемые системы единиц Гаусса и Хевисайда-Лоренца Джексон Классическая электродинамика , может дать студентам вводного курса более прямой путь к пониманию. Согласно предисловию к 3-му изданию, напряжение между СИ и гауссовыми единицами привело к разделению книги Джексона на две системы единиц и предательство договор между друзьями.Упрощение, описанное выше можно сделать, заменив только единицы для магнитной индукции B , векторный потенциал A , и магнитный поток Φ _B в электрическое поле единиц, то есть [В / м], [В] и [Вм] соответственно, с компенсационным c ценности, добавленные в уравнения Максвелла, чтобы сохранить все остальное (включая H) то же самое. Какие еще плюсы и минусы сделать этот сдвиг, по крайней мере, для вводных классов физики жаждете как можно более ясного взгляда на взаимосвязи природы?

^[4] Правильное ускорение и собственная сила не более чем 3-х векторное ускорение и чистая сила, испытываемая в кадр ускоряемого объекта.Как собственное время и собственной длины , они описывают количества с точки зрения специальной рамы, в данном случае рамы объекта, к которому относятся ускорение и силы применяемый. Их величина также является лоренц-инвариантной величиной четырех векторов ускорения и чистой силы , видимых со всех сторон кадров , так как в остальном кадре ускоряемого объекта времениподобная составляющая этих четырех векторов равна нулю.Потому что силы могут быть вызваны объектами, движущимися относительно одного другая, правильная сила F _o не подчиняется принцип действия-противодействия как 4-векторные и локально определенные силы, зависящие от рамы. Однако это отличный мост между локально измеренными координатами-ускорениями a и усилие F = d p / dt, так как F _o точно м а γ ³ / γ _⊥ в то время как F отличается от F _или тем, что компонент, параллельный F _o делится на γ _⊥ при вращении к линии скорости.Принцип эквивалентности общей теории относительности в сочетании с концепция локальных сил аффинной связи (или геометрических), делает эти количества полезными даже в неинерциальных условиях (например, гравитационно искривленное пространство-время). Полезность законов Ньютона для описания гравитации на Земля как «еще одна сила между объектами» является живым доказательством этого, поскольку гравитация, как и магнетизм, является примером повседневного относительность.

---

Подробнее

• р.Г. Пиччони недавний статья в Учитель физики .
• Заметки Дэна Шредера о Перселле упрощенный.
• Подробнее на зарядах, движущихся около нулевого провода с током.
• Эта записка обсуждает приведенное выше значение собственной силы более подробно.
• Дополнительные примечания к правильные количества и движение на основе карты с любой скоростью.

Таблица преобразования единиц плотности магнитного потока ・ напряженности магнитного поля ｜ KOHDEN Co., ООО

НАЧАЛЬНАЯ СТРАНИЦА> Датчик AMR> Таблица преобразования единиц плотности магнитного потока ・ Напряженность магнитного поля

Инструмент преобразования единиц магнитного поля

Преобразование единиц плотности магнитного потока и плотности магнитного поля может быть выполнено с помощью следующего инструмента.
Введите числа, выбрав единицы в раскрывающемся меню.

Ссылка: Магнитное поле

Напряженность магнитного поля определяется векторным полем, которое имеет направление и величину (или силу).
Число линий магнитного потока, которые проходят через единицу площади перпендикулярно магнитному полю. называется плотностью потока B.
Связь между магнитной силой H и плотностью потока B может быть определена как B = μH.
мкм в данном случае — проницаемость, единица магетизируемости.
В воздухе μ обычно около 1, за исключением особых случаев, и 1 Гаусс ≒ 1 Эрстед.
Обычно напряженность магнитного поля определяется в единицах Э А / м (Эрстед ・ Ампер / метр).
И когда это определяется плотностью потока, используются единицы G (Гаусс) или Т (Тесла).
Это означает, что плотность потока B — это значение, которое включает в себя намагничиваемость, а магнитный поток H не учитывает. включить намагничиваемость.
Во многих случаях используются остаточная плотность магнитного потока (Br) и магнитная коэрцитивная сила (Hc). определить свойства постоянных магнитов.
Oe (Эрстед) используется для определения магнитной коэрцитивной силы, поскольку это сила магнитного поля. для изменения направления магнитного полюса.

〈таблица преобразования единиц напряженности магнитного поля〉

	Наименование единицы	условное обозначение	Коэффициент преобразования единиц СИ
магнитное поле （H）	Эрстед	Oe
	Ампер / метр	А / м	1кА / м = 12.54Oe

	Наименование единицы	условное обозначение	Коэффициент преобразования единиц СИ
плотность потока (B)	Гаусс	GS, G
	тесла	Т	0,1 мТл = 1 г

〈таблица преобразования〉

		Чтение	г	мТ	Oe	кА / м
1	г	Гаусс	–	0.1	1	0,07977
1	мТ	милли тесла	10	–	10	0,7977
1	Oe	Эрстед	1	0,1	–	0,07977
1	кА / м	килоампер на метр	12. No related posts. Разное Похожие записи Как правильно промывать нос при насморке: эффективные методы и растворы 18.11.2024 Питание кормящей мамы: что можно есть при грудном вскармливании 17.11.2024 Лучшая зимняя обувь для детей 2 лет: выбираем комфортные и надежные модели 16.11.2024 Детская комната для новорожденного: оформление, дизайн и планировка 15.11.2024 Увлажнитель воздуха: польза и вред для здоровья, отзывы специалистов и пользователей 14.11.2024 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт +7 495 120-13-73, 8 800 500-97-74; [email protected] [email protected] Карта сайта