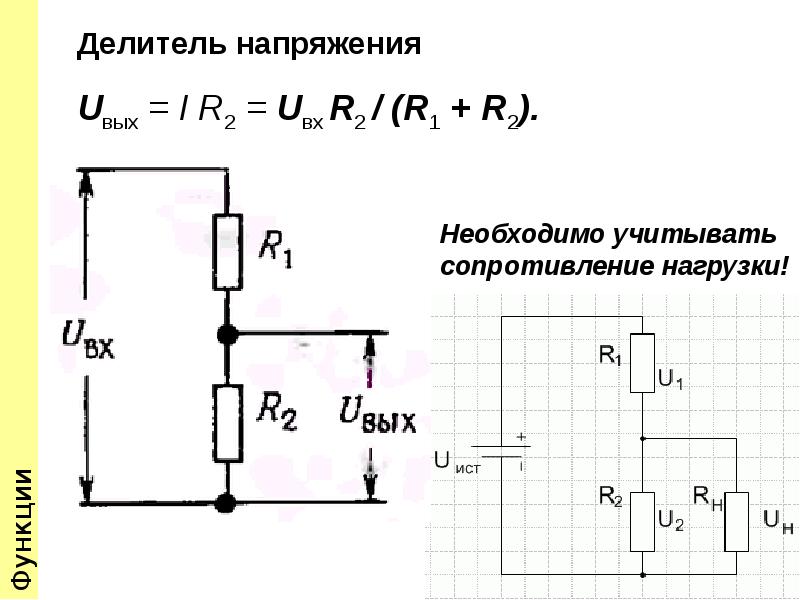
Делитель напряжения
2.7. Делитель напряжения
Достаточно часто в некоторых участках схемы необходимо иметь величину напряжения меньше, чем напряжение источника питания. В этом случае можно использовать делитель напряжения на резисторах (рис. 2.5а). Изменяя соотношение между величинами сопротивлений R1 и R2, на выходе делителя можно получить любое значение напряжения, но не более входного. Выходное напряжение делителя при бесконечно большом сопротивлении нагрузки можно рассчитать по формуле
(2.14)
Для объяснения принципа работы электронных схем необходимо хорошо представлять работу делителя напряжения на резисторах. Можно выделить три задачи, которые необходимо быстро решать при рассмотрении принципа работы электронных устройств, содержащих делитель напряжения:
1. Как и почему
изменяется выходное напряжение делителя, если входное напряжение не
изменяется (постоянное напряжение или переменное напряжение с
неизменяющейся со временем амплитудой),
сопротивление резистора R
2. Как и почему
изменяется выходное напряжение делителя, если входное напряжение не
изменяется (постоянное напряжение или переменное напряжение с
неизменяющейся со временем амплитудой),
сопротивление резистора R1 не изменяется, а сопротивление
резистора R2 увеличивается (уменьшается)?
Как и почему
изменяется выходное напряжение делителя, если входное напряжение не
изменяется (постоянное напряжение или переменное напряжение с
неизменяющейся со временем амплитудой),
сопротивление резистора R1 не изменяется, а сопротивление
резистора R2 увеличивается (уменьшается)?
3. Как и почему
изменяется выходное напряжение делителя, если сопротивления резисторов R
Для всех трех задач дать ответ на поставленный вопрос можно, проанализировав формулу (2.14) для определения выходного напряжения делителя. Решить указанные задачи можно и другим способом.
В первой задаче для определения изменения выходного напряжения воспользуемся формулой Uвых=Iд×R2. Так как сопротивление резистора R2 неизменно, то для ответа на вопрос задачи достаточно выяснить, как будет изменяться ток Iд при увеличении (уменьшении) сопротивления резистора R1
 При
увеличении сопротивления резистора R1 общее сопротивление
последовательно соединенных резисторов R1 и R2 будет
увеличиваться и при неизменном входном напряжении делителя будет уменьшаться
ток делителя Iд (по закону Ома для участка цепи). Уменьшение тока делителя при
неизменном сопротивлении резистора R2 приведет к уменьшению
выходного напряжения.
При
увеличении сопротивления резистора R1 общее сопротивление
последовательно соединенных резисторов R1 и R2 будет
увеличиваться и при неизменном входном напряжении делителя будет уменьшаться
ток делителя Iд (по закону Ома для участка цепи). Уменьшение тока делителя при
неизменном сопротивлении резистора R2 приведет к уменьшению
выходного напряжения.При уменьшении сопротивления резистора R1 сила тока в цепи увеличивается и увеличивается выходное напряжение.
Во второй задаче при увеличении сопротивления
резистора R Поскольку сила тока Iдуменьшается, а сопротивление R1
Поскольку сила тока Iдуменьшается, а сопротивление R1
В третьей задаче при увеличении (уменьшении) входного напряжения выходное напряжение делителя увеличивается (уменьшается), поскольку увеличивается (уменьшается) сила тока Iд.
где
Uвх и Uвых — входное и выходное напряжение делителя, а Iди Iн — ток делителя и ток
нагрузки.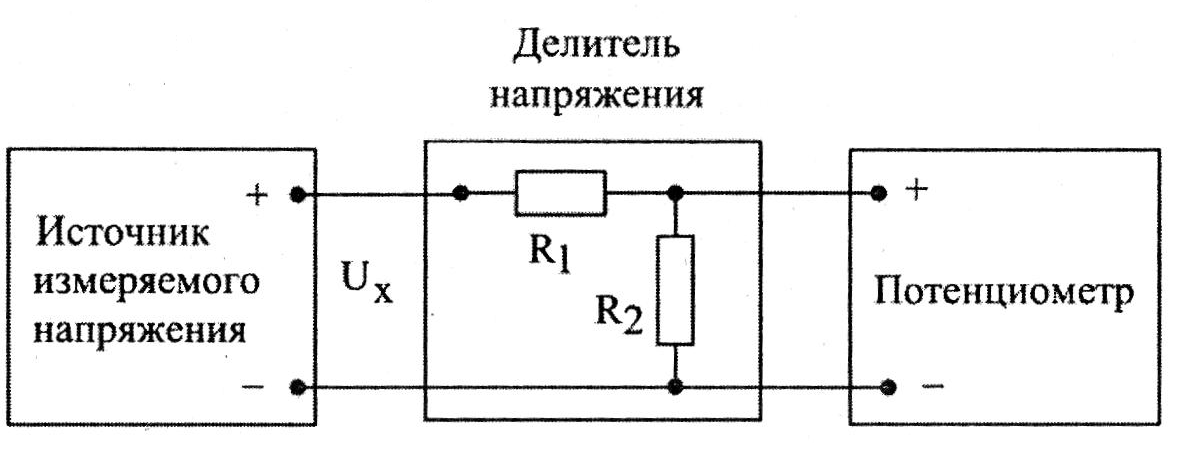
Делители напряжения рекомендуется использовать при малой силе тока нагрузки и небольших ее колебаниях.
В качестве делителя можно использовать потенциометры, в которых плавно изменяется отношение входного и выходного напряжений (рис.
Иногда требуется очень точно и плавно регулировать выходное напряжение делителя. Такую задачу можно решить, используя одну из двух схем делителя, приведенных на рисунке 2.6. Если в схеме рисунка
 В схеме рисунка 2.6 б сопротивление резистора
R1
выбирают меньше сопротивления резистора
R2
и резистором R2
выходное напряжение регулируют грубо, а резистором
R1
– точно.
В схеме рисунка 2.6 б сопротивление резистора
R1
выбирают меньше сопротивления резистора
R2
и резистором R2
выходное напряжение регулируют грубо, а резистором
R1
– точно.Расчёт делителя напряжения на резисторах онлайн
Р/л технология
Схема такого делителя предназначена для получения заданного выходного напряжения, которое будет ниже, чем входное. Например, источник напряжения 24 Вольта, в нужно получить 6 Вольт. Самым простым способом решить этот вопрос – это применить делитель напряжения, состоящий из двух споротивлний.
Он применяется, как при проектировании схем, так и по прямому назначению. Для его расчета используются формулы, которые основаны на законе Ома. Эти формулы позволяют подобрать нужный номинал сопротивлений. Потребуется лишь знать сопротивление нагрузки, входное и выходное напряжения. От этого сопротивления зависит, насколько точно удастся рассчитать весь делитель и получить точно указанное выходное напряжение. Как правило, сопротивление нагрузки выше, чем сопротивление делителя напряжения.
Как правило, сопротивление нагрузки выше, чем сопротивление делителя напряжения.
Если неизвестно выходное напряжение, но известно сопротивление и входное напряжения, то неизвестную величину можно вычислить по указанной формуле.
Для того чтобы не считать постоянно по формулам эти величины, были придуманы онлайн-калькуляторы, которые позволяют точно определить значения резисторов или выходного напряжения. Потребуется лишь внести известные величины. Такой расчет можно производить, как на компьютере, с доступом в сеть Интернет, так и при помощи смартфона. Это значительно экономит время и дает стабильную точность расчетов.
Стоит отметить, что современные калькуляторы-онлайн могут рассчитать и мощность, на которую должен быть установлен резистор.
В радиоэлектронике делители напряжения представлены и в готовых конструктивных решениях. Ими служат, к примеру, переменные резисторы и фоторезисторы, которые имеют возможность менять значение сопротивления, при повороте ручки потенциометра или попадании света.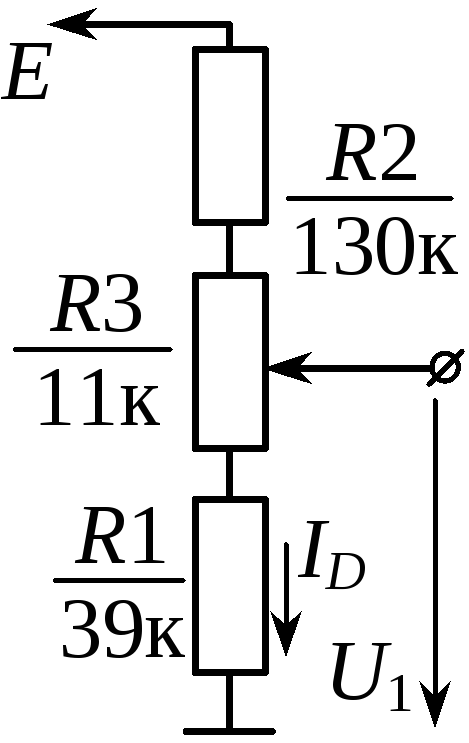 В переменном резисторе присутствуют три вывода, с которых можно получить два сопротивления.
В переменном резисторе присутствуют три вывода, с которых можно получить два сопротивления.
Автор: RadioRadar
Мнения читателей
Нет комментариев. Ваш комментарий будет первый.
Вы можете оставить свой комментарий, мнение или вопрос по приведенному выше материалу:
Поля, обязательные для заполнения
Добавить
Очистить
Делитель напряжения. Создаем робота-андроида своими руками [litres]
Читайте также
Уровни и регулирование напряжения, компенсация реактивной мощности
Уровни и регулирование напряжения, компенсация реактивной мощности Вопрос. Какие требования предъявляются к устройствам регулирования напряжения?Ответ. Они должны обеспечивать поддержание напряжения на шинах напряжением 3-20 кВ электростанций и подстанций, к которым
Измерения напряжения
Измерения напряжения
Вопрос. Где выполняются измерения напряжения?Ответ. Как правило, выполняются:на секциях сборных шин переменного и постоянного тока, которые могут работать раздельно, а также на линиях электропередачи при отсутствии сборных шин РУ подстанции (схемы
Где выполняются измерения напряжения?Ответ. Как правило, выполняются:на секциях сборных шин переменного и постоянного тока, которые могут работать раздельно, а также на линиях электропередачи при отсутствии сборных шин РУ подстанции (схемы
Измерительные трансформаторы напряжения
Измерительные трансформаторы напряжения Вопрос. Что входит в объем испытаний измерительных ТН?Ответ. В объем испытаний входит: для электромагнитных ТН:измерение сопротивления изоляции обмоток;испытание повышенным напряжением частоты 50 Гц;измерение сопротивления
Защита генераторов, работающих непосредственно на сборные шины генераторного напряжения
Защита генераторов, работающих непосредственно на сборные шины генераторного напряжения
Вопрос.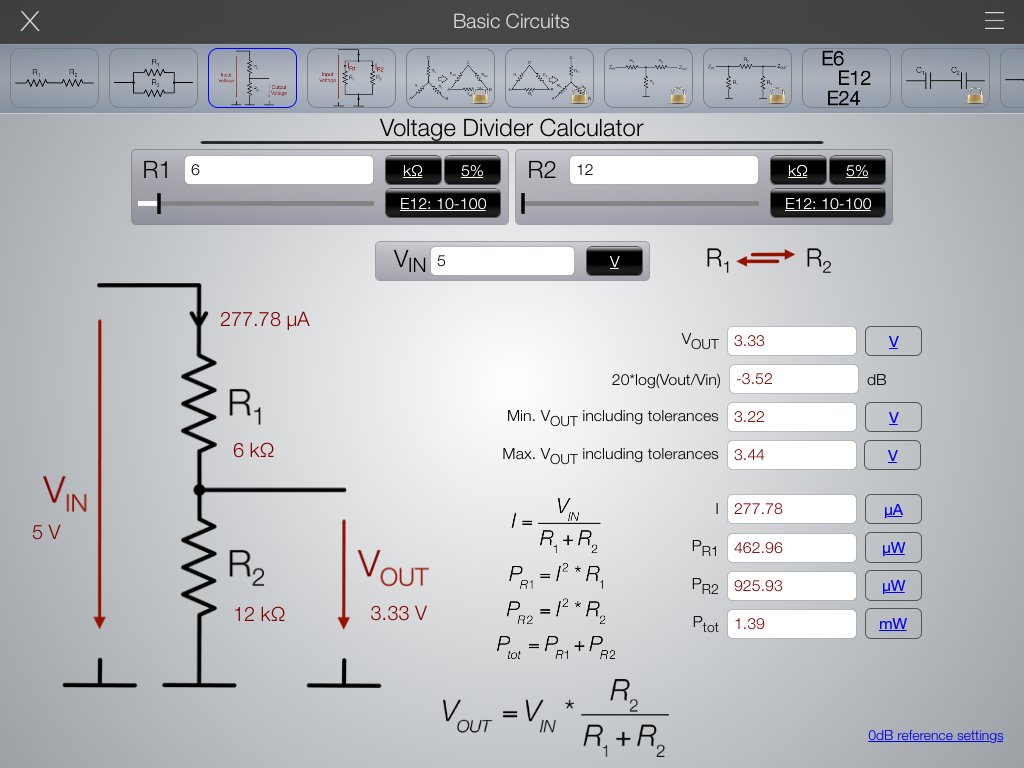
Автоматическое регулирование возбуждения, напряжения и реактивной мощности
Автоматическое регулирование возбуждения, напряжения и реактивной мощности Вопрос. Для каких целей предназначаются системы и устройства автоматического регулирования возбуждения, напряжения и реактивной мощности?Ответ. Предназначаются для:поддержания необходимых
Автоматическое ограничение снижения напряжения (АОСН)
Автоматическое ограничение повышения напряжения (АОПН)
Автоматическое ограничение повышения напряжения (АОПН)
Вопрос. Для каких целей предназначены устройства АОПН?Ответ. Предназначены для ограничения длительности повышения напряжения на электрооборудовании энергосистемы, вызванного односторонним отключением линий
Для каких целей предназначены устройства АОПН?Ответ. Предназначены для ограничения длительности повышения напряжения на электрооборудовании энергосистемы, вызванного односторонним отключением линий
3.8. Датчик пропадания сетевого напряжения со звуковой индикацией состояния
3.8. Датчик пропадания сетевого напряжения со звуковой индикацией состояния Рассмотрим простое в построении устройство датчика отключения электроэнергии со звуковым сигнализатором состояния, электрическая схема которого представлена на рис. 3.13. Устройство
9. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ И КОМПЛЕКТНЫЕ УСТРОЙСТВА НИЗКОГО НАПРЯЖЕНИЯ (ДО 1000 В)
9. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ И КОМПЛЕКТНЫЕ УСТРОЙСТВА НИЗКОГО НАПРЯЖЕНИЯ (ДО 1000 В) В данном разделе приведены указания по ремонту следующих групп аппаратов общепромышленного назначения напряжением до 1000 В: рубильники и переключатели, автоматические воздушные выключатели,
10.
 ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ ВЫСОКОГО НАПРЯЖЕНИЯ (ВЫШЕ 1000 В) И СИЛОВЫЕ ПРЕОБРАЗОВАТЕЛИ
ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ ВЫСОКОГО НАПРЯЖЕНИЯ (ВЫШЕ 1000 В) И СИЛОВЫЕ ПРЕОБРАЗОВАТЕЛИ
10. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ ВЫСОКОГО НАПРЯЖЕНИЯ (ВЫШЕ 1000 В) И СИЛОВЫЕ ПРЕОБРАЗОВАТЕЛИ В данном разделе приведены нормативы и указания по ремонту следующих аппаратов высокого напряжения и силовых преобразователей: выключатели масляные, воздушные и электромагнитные;
1.8.18. Измерительные трансформаторы напряжения
1.8.18. Измерительные трансформаторы напряжения Вопрос 76. Какими должны быть измеренные значения сопротивления изоляции электромагнитных трансформаторов напряжения?Ответ. Эти значения должны быть не менее приведенных в табл. 1.8.15 (п. 1.1).Таблица 1.8.15Сопротивление изоляции
Глава 24 Гравитация и упругие напряжения
Глава 24 Гравитация и упругие напряжения
Наиболее подробно, данная тема раскрыта в работах Ю. Г. Белостоцкого, Санкт – Петербург. Мы были с ним знакомы по конференциям, и я проводил ряд экспериментов по его методике в 1996–1998 годах.Белостоцкий писал в книге «Что такое время?»
Г. Белостоцкого, Санкт – Петербург. Мы были с ним знакомы по конференциям, и я проводил ряд экспериментов по его методике в 1996–1998 годах.Белостоцкий писал в книге «Что такое время?»
45. Измерение сил, моментов и напряжения
45. Измерение сил, моментов и напряжения Общие методы измерения этих величин следующие.1. Измерение проводится непосредственно путем обеспечения прямого контакта прибора с измеряемой величиной.2. Измеряют деформации (в детали или в ее модели), после пересчитывают
6.4.2. АППАРАТЫ ВЫСОКОГО НАПРЯЖЕНИЯ
6.4.2. АППАРАТЫ ВЫСОКОГО НАПРЯЖЕНИЯ
Выключатели высокого напряжения. Выключатель является одним из основных видов ЭА, обеспечивающих включение и отключение электрических цепей с различными токами, в том числе токами перегрузки и коротких замыканий. В начале XX в. появились
В начале XX в. появились
| Если взять один кирпич — мало толку в нем! Но если это один резистор — это уже схема ограничения тока и гашения излишнего напряжения. Два резистора -это уже делитель.
Делитель напряжения. Общий ток через резисторя R1+R2 определится по формуле: I=U1/(R1+R2), а напряжени на выходе делителя будет, соответственно, равно:U2=IR2=U1R2/(R1+R2) | |
| Делители обычно служат для уменьшения сигнала. Если рассмотреть переменный резистор — его средний отвод является выходом делителя с регулируемым коэффициентом деления. Данная схема с успехом используется в регуляторах громкости, записи, тембра, скорости и др. | |
Разделительный конденсатор используют для отделения постоянной составляющей от переменной. Реактивное сопротивление разделительного конденсатора C1 должно быть гораздо меньше, чем резистора R1.
При обратном условии данную схему можно использовать как дифференцирующую цепь в импульсных схемах.
При перепаде напряжения на входе (см. рисунок) на выходе откликом будет короткий импульс. Реактивное сопротивление разделительного конденсатора C1 должно быть гораздо меньше, чем резистора R1.
При обратном условии данную схему можно использовать как дифференцирующую цепь в импульсных схемах.
При перепаде напряжения на входе (см. рисунок) на выходе откликом будет короткий импульс. | |
| Если поменять конденсатор и резистор местами и при условии, что емкость конденсатора достаточно велика (100…1000 мкФ), а сопротивление резистора мало (10…100 Ом) — мы получим прекрасную интегрирующую цепь, обычно используемую в качестве фильтров в блоках питания. При подаче полуволны переменного напряжения с выхода выпрямителя на выходе данной цепи имеем достаточно стабильное постоянное напряжение. | |
Для лучшей фильтрации на входе цепи обычно ставят накопительный конденсатор.
Данная схема — простейший П-образный фильтр, достаточно часто используемый в источниках питания.
Емкости конденсаторов 100…1000 мкФ, а сопротивление резистора 10…100 Ом.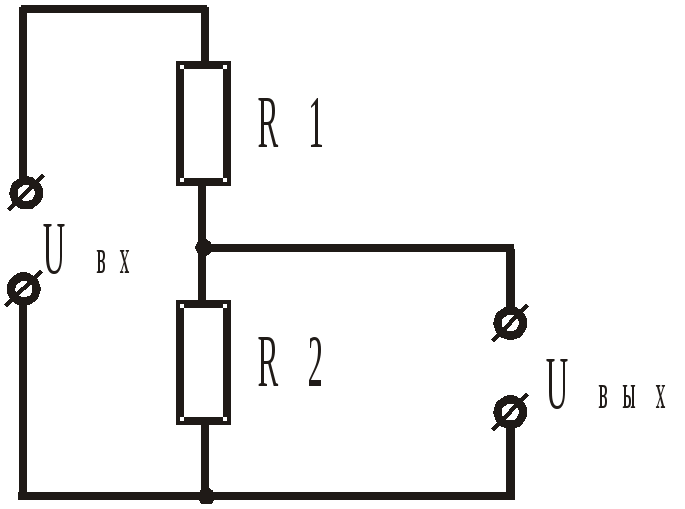 | |
| При больших токах на сопративлении фильтра падает большое напряжение. Снизть потери позволяетт применение дроселя. Эффективность фильтра возрастае во много раз. Но одновреиенно возрастает и стоимость и сложность изготовления схемы. Значительно повысить эффективность можно применив электронный транзисторный фильтр. Но об этом несколько позже. | |
| Для понижения напряжения сети до требуемого уровня служат трансформаторы. Их к.п.д. на малых мощностях порядка 60%. Ток покоя (без нагрузки) обычно 20…40 мА. У торообразных 6..20 мА. | |
Питают схему, как правило от сети переменного тока 220 В через понижающий трансформатор (Т1). Пониженное трансформатором переменное напряжение выпрямляют диодом (VD), который пропускает одну полуволну переменного напряжения. Далее ставят описанные выше фильтры. К сожалению во время второй, непропущенной полуволны схема питается только от конденсаторов фильтра, а потому данное включение применяют обычно только в преобразователях напряжения работающих на высоких частотах (обычно 2-15 кГц). Это повышает эффективность фильтрации в 400-3000 раз соответственно. Это повышает эффективность фильтрации в 400-3000 раз соответственно. | |
| Для уменьшения уровня пульсаций применяют конденсатор в качестве простейшего фильтра. | |
| При питани же от промышленной сети 220 В в качестве выпрямтиеля используют мостовое включение из четырех диодов. При положительной полуволне напряжения работают диоды VD3 и VD2, а при отрицательной VD1 и VD4. Таким образом ток в нагрузке течет все время в одном направлении. | |
| Иногда используют схемы удвления напряжения. Такая схема,как правило, применяется для включения с незаземленной нагрузкой. | |
| Если же нагрузку необходимо заземлить — применяется схема удвоения с общим проводом на одном из плеч нагрузки. | |
| Индикатором включения питания служит следующая схема. Резистор R необходим для ограничения тока светодиода до допустимого уровня. | |
| Эти клетки заполним позже! | |
| И эти тож 🙂 |
Делитель напряжения, что это такое и как он работает разбираем на практике | Энергофиксик
Так что ;t такое делитель напряжения? Если обратиться к википедии, то там записано следующее определение: изделие, в котором входное и выходное напряжения связаны между собой определенным коэффициентом передачи. Звучит не очень понятно. В этой статье я постараюсь рассказать о делителе напряжения простым языком.
Звучит не очень понятно. В этой статье я постараюсь рассказать о делителе напряжения простым языком.
Содержание
Существующие виды делителей напряжения
Немного теории и скучных формул
Закрепляем на практике
Переменный резистор
Заключение
Существующие виды делителей напряжения
Делители напряжения бывают линейными и нелинейными. В свою очередь линейные подразделяются на:
1. Резистивные;
2. Емкостные;
3. Индуктивные.
А к нелинейным относятся, например, параметрические стабилизаторы напряжения.
Хочется заметить, что принцип работы любого делителя одинаков и различия обусловлены лишь набором компонентов, из которых он собран. Поэтому в качестве примера будет рассмотрен резистивный делитель напряжения, как наиболее простой из всех существующих.
Давайте рассмотрим следующий рисунок:
Выше представленная схема выполнена из пары резисторов соединенных последовательно. К такой схеме мы можем спокойно прилагать как постоянное, так и переменное напряжение. И как только мы подключим такую схему, то в силу вступит Закон Ома, который позволит нам многое подсчитать.
Итак, при последовательном соединении резисторов их сопротивление будет равняться сумме, а именно: R1+R2. И получается что сила тока, будет такова:
Также учтите, что при таком соединении резисторов сила тока будет одинакова на любом участке цепи.
Итак, так как у нас резисторы имеют разное сопротивление, то согласно Закону Ома, напряжение на этих элементах так же будет различно, то есть на резисторе R1 будет U1, а на R2 будет U2.
Зная это, мы можем высчитать силу тока уже так:
Выполняя простые преобразования, конечные формулы для расчета выходного напряжения будет иметь следующий вид:
Получается, что по этим формулам мы сможем подсчитать, какое падение напряжение будет на каждом из резисторов.
Проще говоря, при последовательном соединении резисторов на каждом из них будет свое напряжение и сумма этих напряжений будет равна напряжению источника питания, то есть будет справедливо следующее выражение:
То есть с помощью резисторов произошло простое деление напряжения пришедшего от источника питания.
Закрепляем на практике
Итак, со скучной теорией закончили, давайте проведем практический эксперимент. Для этого берем парочку резисторов (разного номинала), источник питания и мультиметр.
Производим измерение сопротивления наших резисторов:
На блоке питания выставляем, например, 10 В, а резисторы соединяем между собой последовательным образом:
Теперь производим измерение напряжения на первом резисторе, а затем на втором:
Теперь складываем наши полученные напряжения:
3.307 В + 6,76 В = 10,067 Вольт. Разница в 0,067 Вольт спишем на погрешность мультиметра и самого блока питания.
Разница в 0,067 Вольт спишем на погрешность мультиметра и самого блока питания.
Вот мы и рассмотрели самый простейший пример деления напряжения.
Теперь для полноты эксперимента убедимся на практике, что сила тока неизменна во всей нашей сети при последовательном соединении.
Как видно из выше представленных фотографий, ток везде одинаков.
Переменный резистор
Для плавного деления напряжения используются регулируемые резисторы.
Принцип данного резистора таков: между двумя крайними точками 1 и 3 присутствует постоянное сопротивление. А сопротивление среднего вывода по отношению к крайним изменяется, если крутить построечную рукоять.
Выставляем на нашем блоке питания 10 Вольт и производим измерение напряжения между крайними контактами:
Теперь с помощью регулятора выставляем любое положение и измеряем напряжение на выводах 1-2 и 2-3
Все так же суммируем получившиеся значения 6,87+3,199 = 10,069 Вольт. Лишние 0,069 Вольта все так же списываем на погрешность.
Лишние 0,069 Вольта все так же списываем на погрешность.
Заключение
Конечно, в современной электронике такие делители уже давно не применяются. Но если вы собираете какую-либо самоделку и необходимо выполнить разделение напряжения, то резисторный делитель напряжения подойдет как нельзя лучше. Если статья оказалась вам полезна, то оцените ее лайком. Спасибо за ваше драгоценное внимание!
Почему последовательная цепь сопротивлений называется делителем напряжений и как он работает.
Чтобы понять, почему именно последовательную цепь, состоящую из электрических сопротивлений, называют делителем напряжений давайте с Вами разберемся в основах электрофизики. Хотя, если вдуматься в само название этого вопроса, можно и самому догадаться, что если имеется последовательная цепь из резисторов, то на каждом из них по идее должно оседать какая-то определённая часть электрического напряжения. Следовательно, мы как бы делим одно общее напряжение на некоторые его части, величина которых нам нужна для каких-то своих нужд.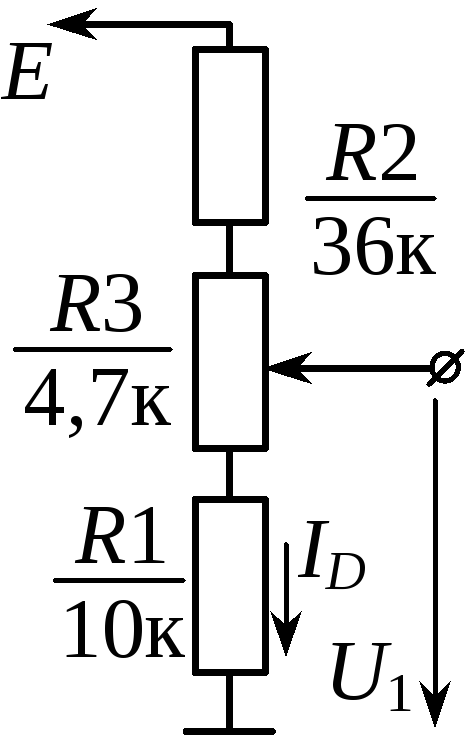
Итак, электрическое напряжение — это разность электрических потенциалов между двумя различными точками. Если взять обычный резистор (имеющее некоторое сопротивление, пусть 10 Ом), и к нему приложить напряжение, к примеру величиной в 12 вольт, то через резистор потечет электрический ток величиной в 1,2 ампера (по закону ома мы напряжение делим на сопротивление). При этом если щупами вольтметра прикоснутся к выходу источника питания, а потом непосредственно к нашему резистору, то убедимся, что напряжение будут совпадать (возможно с очень малой разницей по причине оседания напряжения на самих проводах, если они достаточно длинны).
Теперь вместо одного резистора на 10 Ом мы поставим два последовательно соединенных резистора, каждый из которых по 5 Ом (при последовательном соединении сопротивлений их номиналы слаживаются). Подсоединив всё тот же блок питания на 12 вольт и измерив напряжение на каждом из резисторов мы увидим что напряжение поделилось поровну. На каждом резисторе осело ровно по 6 вольт.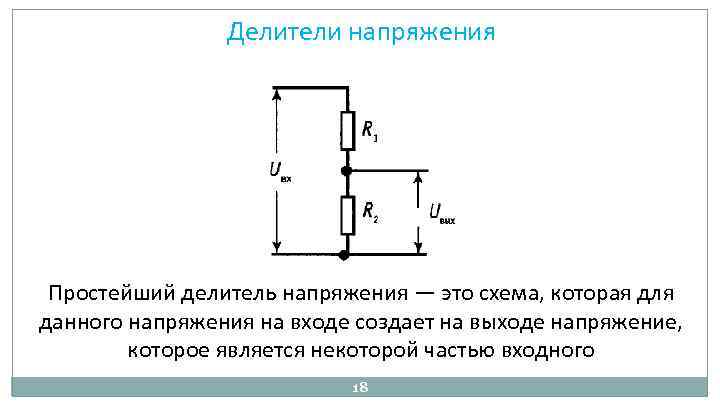 Это потому что сопротивления одинаковой величины. Если мы поставили три одинаковых резистора то и напряжение разделилось бы поровну на три части (по 4 вольта). Ну думаю смысл деления понятен.
Это потому что сопротивления одинаковой величины. Если мы поставили три одинаковых резистора то и напряжение разделилось бы поровну на три части (по 4 вольта). Ну думаю смысл деления понятен.
А что если резисторы будут разной величины (соединение их также последовательное) ? Тогда электрическое напряжение поделится прямо пропорционально их сопротивлению. Узнать на каком какое осядет напряжения можно либо просто измерив его вольтметром, либо же путём применения формулы закона Ома, но для этого мы должны знать силу тока, что будет протекать по этой последовательной цепи. И чтобы узнать напряжение на резисторе нужно силу тока (в Амперах) умножить на его сопротивление (в Омах). Ну, и так для каждого резистора, где нужно узнать напряжение.
На примере последовательно соединённых резисторов мы увидели сам принцип деления напряжения. Более распространенным вариантом делителя напряжения является использование переменного (подстроечного) резистора, имеющего три вывода (два основных, имеющие общее сопротивление данного резистора и один вывод, идущий от ползунка, смещающегося между этими двумя основными).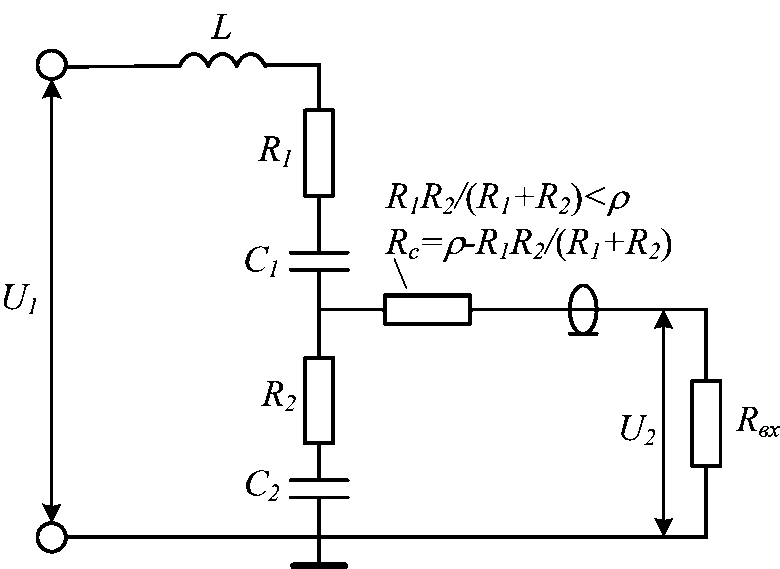 В схемах делителя напряжения его подключают так: один вывод (из основных) является общим, второй из основных является местом, куда прилаживается общее напряжение, ну, а с вывода, идущего от ползунка, относительно общего провода, снимается более низкое напряжение, величину которого можно выставить ручкой этого переменного резистора. Данный вариант делителя напряжения повсеместно используется в регуляторах громкости, тембра и т.д.
В схемах делителя напряжения его подключают так: один вывод (из основных) является общим, второй из основных является местом, куда прилаживается общее напряжение, ну, а с вывода, идущего от ползунка, относительно общего провода, снимается более низкое напряжение, величину которого можно выставить ручкой этого переменного резистора. Данный вариант делителя напряжения повсеместно используется в регуляторах громкости, тембра и т.д.
Итак, мы выяснили, что приложенное электрическое напряжение на цепочку последовательно соединенных резисторов будет делится пропорционально сопротивлению, которым обладает каждый из них. Может возникнуть вопрос (если коснуться практического применения делителя напряжения в конкретных схемах), а что при этом сопротивления могут быть совсем разные? Для получения нужной величины именно напряжения, то да, лишь бы соблюдался принцип пропорциональности. Но вот если в схеме имеет значение сила тока, текущего через этот самый делитель напряжения, то тут уж величина сопротивлений имеет значение.
Допустим нам нужно использовать делитель напряжения для регулируемого блока питания. В обычной схеме такого блока питания имеется параметрический стабилизатор в виде опорного стабилитрона. Стабилитроны не рассчитаны на большие токи (через них в рабочем состоянии протекают десятки миллиампер). Следовательно параллельно подключенный к стабилитрону делитель напряжения (в виде обычного переменного резистора) также не будет пропускать через себя большие токи. Посему номинал переменного резистора для делителя напряжения берется обычно в пределах 1-10 килоОм.
В электрических схемах делители напряжения встречаются на каждом шагу. Именно эти делители позволяют получать нужное значения электрического напряжения в тех или иных узлах схемы. В более простом варианте роль данного делителя выполняют обычные постоянные и переменные резисторы. Хотя при усложнении схемы уже могут использоваться цифровые варианты и аналоги, что дает свои преимущества.
P.S. Понимая общий принцип работы и само назначение делителя напряжения вы уже легко сможете распознавать эту функциональную часть в различных электрических и электронных схемах.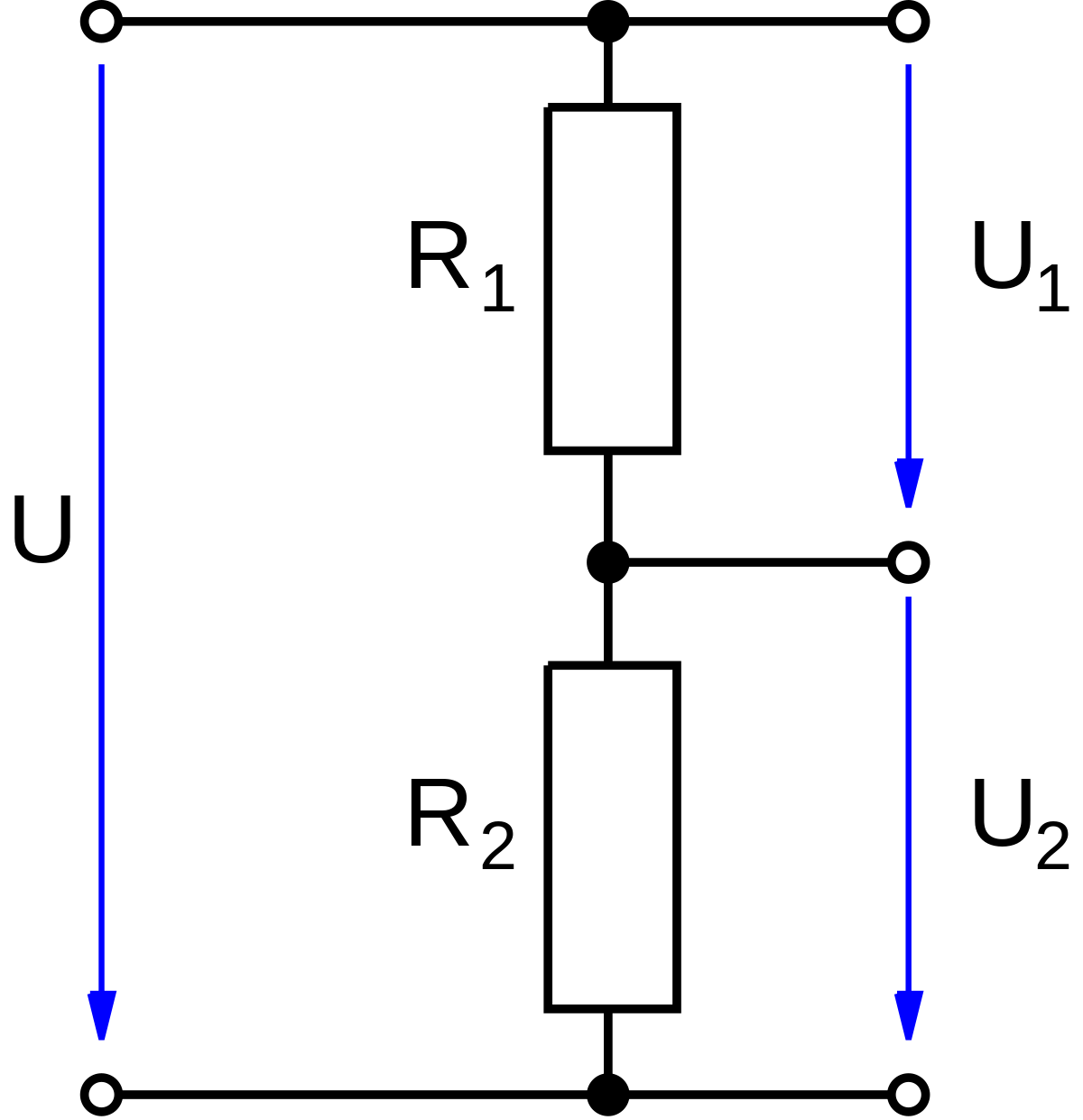 При некоторой практике сами начнете широко их использовать в тех или иных схемах (обычно начинают с самодельных регулируемых блоков питания).
При некоторой практике сами начнете широко их использовать в тех или иных схемах (обычно начинают с самодельных регулируемых блоков питания).
Введение
Введение
Потенциометр — это трехполюсный резистор со скользящим или вращающимся контактом. Это регулируемый делитель напряжения с двумя статическими контактами и одним подвижным контактом. Подвижный вывод представляет собой стеклоочиститель, который перемещается через элемент сопротивления, обычно по дуге, управляемой поворотной ручкой. Вращение ручки дает логометрическое деление потенциала на резистивном элементе. Потенциометр обычно используется в динамиках и ресиверах для регулировки громкости.Кроме того, он не может напрямую управлять двигателем, потому что его мощность слишком мала.
1 Схема подключения потенциометра
Потенциометр может использоваться как трехконтактный или двухконтактный компонент. Последний можно рассматривать как реостат. Для обычного потенциометра (три контакта) ползунок рядом с центром представляет собой провод сопротивления. Два контакта на обоих концах провода сопротивления подключены к входу и заземлению (некоторые не подключены) соответственно. То есть один вывод подключен к входному сигналу, а другой вывод заземлен.В это время провод сопротивления имеет общее значение сопротивления на двух участках. Вы перемещаете скользящую деталь, чтобы пройти через этот провод сопротивления, чтобы получить переменное сопротивление. Если входные и выходные сигналы меняются местами, направление скольжения ползуна противоположно изменению сопротивления.
Для обычного потенциометра (три контакта) ползунок рядом с центром представляет собой провод сопротивления. Два контакта на обоих концах провода сопротивления подключены к входу и заземлению (некоторые не подключены) соответственно. То есть один вывод подключен к входному сигналу, а другой вывод заземлен.В это время провод сопротивления имеет общее значение сопротивления на двух участках. Вы перемещаете скользящую деталь, чтобы пройти через этот провод сопротивления, чтобы получить переменное сопротивление. Если входные и выходные сигналы меняются местами, направление скольжения ползуна противоположно изменению сопротивления.
Рис. 1. Структура потенциометра
1) Для потенциометра (или подстроечного резистора) с традиционными выводами (три контакта) сопротивление на обоих концах является фиксированным, а сопротивление среднего вывода — переменным.То есть клеммы с обеих сторон потенциометра — это полное сопротивление, а середина меняется. Например, источник питания подключается от любого одного контакта на сторонах резистора и выводится от среднего контакта, а напряжение изменяется при вращении среднего контакта.
2) Хотя сопротивление может изменяться в зависимости от ползунка, общее значение сопротивления контактов является фиксированным. В это время потенциометр приравнивается к регулятору тока, и выбранные выходные клеммы тока должны быть скользящей клеммой.
Рис. 2. Потенциометр как делитель напряжения
3) Если потенциометр используется в качестве переменного делителя напряжения, один контакт подключается к входному напряжению, средний контакт подключается к выходному напряжению, а другой контакт может быть заземлен. Когда вращающаяся ручка или скользящая ручка потенциометра срабатывают, подвижный контакт скользит по резистору. В это время выходное напряжение имеет определенную взаимосвязь с внешним напряжением, углом стеклоочистителя и ходом хода.
4) Если потенциометр используется в качестве переменного резистора, один конец подключается к входному напряжению, средний конец подключается к выходу, а другой конец может быть подвешен или подключен к среднему концу для получения плавного и непрерывного изменения значение сопротивления.
Рисунок 3. Цепь потенциометра
2 Основы потенциометра делителя напряжения
1. Резистор потенциометра в основном изготовлен из поликарбонатной синтетической смолы. Следует избегать следующих продуктов: аммиак, другие амины, водные растворы щелочей, ароматические углеводороды, кетоны, липидные углеводороды, сильнодействующие химические вещества (избыточный pH) и т. Д.В противном случае это повлияет на работу потенциометра.
2. При пайке клемм потенциометра избегайте использования емкостного флюса, который может вызвать окисление металла и образование плесени. При использовании флюса плохого качества плохая пайка может вызвать проблемы при пайке, что приведет к плохому контакту или обрыву цепи.
3. Если температура пайки клеммы слишком высока или время пайки слишком велико, это может привести к повреждению потенциометра. Температурный диапазон съемного потенциометра составляет 235 ℃ ± 5 ℃; Тип соединения проводов составляет 350 ℃ ± 10 ℃, а точка пайки должна быть больше 1. 5 мм от корпуса потенциометра. Кроме того, избегайте сильного давления на клеммы, в противном случае это может привести к плохому контакту.
5 мм от корпуса потенциометра. Кроме того, избегайте сильного давления на клеммы, в противном случае это может привести к плохому контакту.
4. Во время пайки, высота флюса, входящего в плату печатной машины, должна быть отрегулирована должным образом, и следует избегать воздействия на потенциометр. Потому что это вызовет плохой контакт между щеткой и резистором или приведет к шуму.
5. Потенциометр лучше в структуре регулировки напряжения.
6.Избегайте образования конденсата или капель воды на поверхности потенциометра и избегайте использования потенциометра во влажном месте, чтобы предотвратить повреждение изоляции или короткое замыкание.
7. При фиксации винтов поворотного потенциометра усилие не должно быть слишком большим, чтобы избежать плохого вращения. Для потенциометра прямого скольжения избегайте использования длинных винтов, в противном случае это может затруднить движение скользящей ручки и даже повредить сам потенциометр.
8. В процессе установки потенциометра на ручку толкающее усилие не должно быть слишком большим (не превышать показатель параметра номинального толкающего и тянущего усилия), в противном случае это может привести к повреждению потенциометра.
9. Сила вращения потенциометра будет уменьшаться при повышении температуры и уменьшаться при понижении температуры. Если потенциометр используется в низкотемпературной среде, ему необходима специальная низкотемпературная смазка.
10. Если вал или скользящая рукоятка потенциометра слишком длинные, их легко трясти, что приведет к нестабильности сигнала цепи.
11. Углеродная пленка потенциометра выдерживает температуру окружающей среды 70 ℃, и ее функция может быть потеряна при температуре выше 70 ℃.
12. Для регулируемого потенциометра, когда постоянный ток проходит через подвижный контакт, может возникнуть проблема анодного окисления. В этом случае лучше всего соединить компонент с отрицательным концом, а подвижный контакт — с положительным концом.
13. Ток нагрузки регулируемого потенциометра не может быть увеличен. Для фактического измерения тока включите амперметр последовательно с потенциометром в активной цепи.
14. Не превышайте номинальную мощность при использовании регулируемого потенциометра. Например, когда рассеиваемая мощность превышает номинальное значение, это приведет к перегреву потенциометра.
Например, когда рассеиваемая мощность превышает номинальное значение, это приведет к перегреву потенциометра.
15. Потенциометр чувствителен, он способен измерять очень малую разность потенциалов и показывает значительное изменение длины балансировки при небольшом изменении измеряемой разности потенциалов.
16. Потенциометр постоянного тока создается путем падения напряжения на последовательно включенных резисторах. Разные резисторы будут давать разные значения. В потенциометре переменного тока можно использовать резисторы или даже катушки индуктивности или конденсаторы в качестве импедансов, которые будут снижать напряжение и обеспечивать напряжение, меньшее, чем приложенное напряжение.
17. Если расположить стеклоочиститель потенциометра в центре резистивного элемента, то напряжение на стеклоочистителе составляет 50%; если стеклоочиститель расположен на 1/4 расстояния от отрицательного узла, тогда напряжение стеклоочистителя составляет 1/4 всего напряжения.
18. Номенклатура потенциометров: Обычно используется метод прямой маркировки. Буквы и числа нанесены на корпус потенциометра, чтобы указать их модель, номинальную мощность, сопротивление и соотношение между сопротивлением и углом поворота.
Номенклатура потенциометров: Обычно используется метод прямой маркировки. Буквы и числа нанесены на корпус потенциометра, чтобы указать их модель, номинальную мощность, сопротивление и соотношение между сопротивлением и углом поворота.
3 Измерения потенциометра
Основные требования к проверке потенциометра:
- Значение сопротивления соответствует требованиям схемы.
- Соединение между центральным скользящим концом и резистором хорошее, вращение плавное. Для потенциометра с переключателями действие переключателя должно быть точным, надежным и гибким.
Следовательно, перед использованием необходимо проверить работоспособность потенциометра.
1) Измерение сопротивления: сначала выберите соответствующую передачу мультиметра в соответствии с сопротивлением измеренного потенциометра. Соответствует ли сопротивление между двумя концами переменного тока номинальному сопротивлению. Поверните скользящий контакт, и его значение должно быть зафиксировано. Если сопротивление показывает бесконечность, потенциометр поврежден.
Если сопротивление показывает бесконечность, потенциометр поврежден.
2) Затем измерьте контакт между центральным концом и резистором, то есть сопротивление между двумя концами BC.Метод состоит в том, чтобы установить диапазон сопротивления мультиметра в соответствующем диапазоне. Во время измерения медленно вращайте вал и наблюдайте за показаниями мультиметра. Обычно показания постоянно меняются в одном направлении. Если есть скачок, падение или блокировка, значит, подвижный контакт неисправен.
3) Когда центральный конец скользит к головке или концу, значение сопротивления центрального конца и совпадающего конца равно 0 для идеального состояния. При фактическом измерении будет определенное значение (обычно определяемое номинальным значением, обычно менее 5 Ом), что является нормальным.
Получите дополнительную информацию по номеру Потенциометр — трехконтактный резистор .
Что такое переменный резистор?
Переменные резисторы — это резисторы, которые изменяют сопротивление от нуля до определенного максимального значения. Они обычно используются в качестве регуляторов громкости и регуляторов напряжения.
Переменные резисторыможно разделить на три типа:
- Потенциометры
- Реостаты
- Цифровые потенциометры
Реостат
Предустановленный резистор Потенциометр с
Потенциометры используются для изменения сопротивления в цепи путем поворота поворотной ручки.Потенциометры имеют три контакта. Между двумя боковыми штырями проложена полоса из резистивного материала, который создает сопротивление. Средний штифт — дворник. Это соединение стеклоочистителя находится где-то на полосе между двумя концами. Вы можете переместить точку соединения скребка с резистивным материалом, поворачивая вал потенциометра. При перемещении дворника влево сопротивление между средним штифтом и левым штифтом уменьшается. Затем сопротивление между средним штифтом и правым штифтом увеличивается при перемещении дворника влево.
Типы потенциометров
- Поворотные потенциометры — самый распространенный вид потенциометров. Они используют поворотную ручку для перемещения скребка вокруг резистивного материала.
- Линейные потенциометры — состоят из линейного ползунка, который контролирует положение скребка вдоль резистивного материала.
Потенциометры как делители напряжения
Делитель напряжения — это простая схема, которая может использоваться для понижения напряжения в цепи.Выходное напряжение зависит от соотношения двух последовательно соединенных резисторов. Выходное напряжение берется из точки между двумя резисторами. Чтобы рассчитать выходное напряжение делителя напряжения, используйте уравнение делителя напряжения ниже:
R1 — резистор, ближайший к входному напряжению, R 2 — резистор, ближайший к земле, V in — входное напряжение, а V out — выходное напряжение.
Потенциометры в основном представляют собой регулируемые делители напряжения.
Схема потенциометра
Внутри потенциометра находится единственный резистор и стеклоочиститель, который разрезает резистор на две части и перемещается для регулировки соотношения между обеими половинами. Внешне обычно есть три контакта: два контакта подключаются к каждому концу резистора, а третий подключается к дворнику потенциометра. Если два внешних контакта подключены к напряжению, выход (V из на среднем контакте) будет имитировать делитель напряжения. Если потенциометр полностью повернется в одном направлении, напряжение может быть нулевым.И если он поворачивается на другую сторону, выходное напряжение приближается к входному, а дворник в среднем положении означает, что выходное напряжение будет половиной входного.
Подключение потенциометра- Начните с определения трех клемм на потенциометре. Расположите его валом вверх и тремя выводами к себе. В этом положении вы можете легко идентифицировать клеммы слева направо как клеммы 1, 2 и 3. Заземлите первую клемму потенциометра.
- В этом приложении клемма 1 обеспечивает заземление. Для этого припаяйте оба конца провода к клемме и шасси электрического компонента соответственно. Отмерьте и отрежьте длину провода, необходимого для подключения клеммы к удобному месту на шасси, и припаяйте оба конца провода к клемме и к шасси компонента. Это заземлит потенциометр. И его можно повернуть до нуля в минимальном положении.
- Подключите вторую клемму к выходу схемы, чтобы создать вход потенциометра.К нему должна подключаться входная линия схемы. Припаиваем это соединение так же, как и предыдущее.
- Подключите клемму 3 к входу схемы, поскольку клемма 3 является выходом потенциометра. Припаиваем провод так же, как в первых 2-х выводах.
- После подключения проверьте с помощью вольтметра. Подключите выводы вольтметра к входным и выходным клеммам потенциометра и включите вал. Поворачивая вал по часовой стрелке или против часовой стрелки, можно настроить сигнал на вашем устройстве.
Пример схемы светорегулятора с использованием потенциометра и полевого МОП-транзистора Цифровые Потенциометры
Цифровой потенциометр — это тип переменного резистора, который использует цифровые сигналы вместо механического движения для изменения своего сопротивления. Цифровые потенциометры изменяют сопротивление дискретными шагами в зависимости от посылаемого на него цифрового сигнала. Они отлично подходят для сред, где вибрация, пыль или влага могут забить вал механического потенциометра.
Вот несколько цифровых потенциометров, которые нравятся любителям электроники:
Каждый из следующих цифровых потенциометров от Renesas Electronics имеет 100 различных точек сопротивления, работает от 5 В и управляется трехпроводным последовательным интерфейсом:
Семейство цифровых потенциометров MPC41 / 42 от Microchip также довольно распространено:
- MCP4131 — 129 точек сопротивления, доступные в диапазонах 5 кОм, 10 кОм, 50 кОм и 100 кОм, рабочее напряжение 1.От 8 В до 5,5 В, управление с помощью SPI
- MCP42010 — 256 точек сопротивления, доступные в диапазонах 10 кОм, 50 кОм и 100 кОм, рабочее напряжение от 2,7 В до 5,5 В, управление с помощью SPI
Элегантный подход к разработке делителя переменного напряжения
Делитель напряжения, вероятно, является наиболее распространенной электронной схемой. Несмотря на свою простоту, это может стать проблемой для многих людей, особенно новичков. В этой статье представлен быстрый и точный способ создания переменного делителя напряжения с минимальными математическими расчетами.
На рис. 1-a показана проблема: учитывая значение потенциометра R P , рассчитайте значения R X и R Y , чтобы выходное напряжение могло измениться от -5 до +8 В.
РИСУНОК 1. Исходную схему (a) можно заменить тремя постоянными резисторами (b).
Поскольку значение -5 В будет отображаться на выходе, когда стеклоочиститель находится на нижнем конце потенциометра, а значение + 8 В будет там, когда стеклоочиститель находится на верхнем конце потенциометра, мы можем изменить схему как показано на Рисунок 1-b .
Давайте сначала рассмотрим академический подход. Напишите уравнения для V MAX и V MIN и решите их как систему одновременных уравнений с двумя неизвестными. R X и R Y .
Путем наложения:
Избавьтесь от знаменателей и отправьте члены с R X и R Y в левую часть каждого уравнения:
(V MAX — V EE ) R X + (V MAX — V CC ) R Y = (V CC — V MAX ) R P
(V MAX — V EE ) R X + (V MIN — V CC ) R Y = (V EE — V MIN ) R P
Замена напряжений и R P их числовыми значениями дает:
23R X — 7R Y = 70
10R X — 20R Y = -100
Решение: R X = 5.385 кОм и R Y = 7,692 кОм.
Мы можем сделать ту же работу быстрее и с меньшими математическими усилиями, если воспользуемся небольшим трюком: коэффициент передачи делителя напряжения не меняется, когда ВСЕ значения резистора умножаются на фиксированное число.
Действительно, если два резистора — R1 = 2 кОм и R2 = 5 кОм — подключены к батарее 9 В, выходное напряжение будет:
Если оба резистора в два раза больше или в три раза меньше, выходное напряжение все равно будет 6.43V. Давайте применим это к нашей проблеме. Первым шагом является вычисление падений напряжения на каждом резисторе, как показано на Рис. 2-a .
РИСУНОК 2. Этапы расчета включают отдельные падения напряжения (a), значения промежуточных резисторов (b) и конечную схему (c).
Если предположить, что по сети течет ток 1 мА, то R X должен иметь значение 7 кОм (7 В / 1 мА).
Аналогично, R P должен иметь значение 13 кОм, а R Y должно быть 10 кОм. Рисунок 2-b показывает схему. Однако горшок должен иметь значение 10, а не 13 кОм. Чтобы получить это, нам нужно умножить 13 кОм на 0,769 (10/13).
Чтобы сохранить коэффициенты передачи делителя, мы умножаем два других резистора на такое же число.
Схема 2-c показана. Мы получаем тот же результат без суперпозиции и без вычисления одновременных уравнений.
Моделирование доказывает, что схема работает должным образом (см. Рисунок 3 ).
РИСУНОК 3. Результат моделирования.
Имейте в виду, что большинство потенциометров имеют допуск 10 или 20%; следовательно, рекомендуется сначала измерить реальное сопротивление RP, а затем спроектировать делитель, используя представленную процедуру. В конце сопоставьте рассчитанные значения RX и RY со стандартной серией сопротивлений, например E24 (допуск 5%) или E96 (допуск 1%).
В конце Рисунок 4 показывает три типичных применения делителей напряжения.Первая цепь является входной частью почти каждого цифрового мультиметра (DMM). Аналого-цифровой преобразователь внутри цифрового мультиметра имеет фиксированный диапазон ± 1 В постоянного тока. Делитель напряжения расширяет диапазон измерения до 1000 В постоянного тока.
РИСУНОК 4. Типичные области применения делителей напряжения.
Вторая цепь контролирует напряжение аккумуляторной батареи вилочного погрузчика с помощью аналогового измерителя. Делитель напряжения R1-R2 перемещает начало шкалы счетчика от 0 до 10 В.R M устанавливает конец шкалы на 14 В. Поскольку шкала соответствует напряжению батареи, можно измерить это напряжение с лучшим разрешением.
Третья цепь — регулируемый регулятор напряжения. Благодаря регулируемому делителю напряжения R 1 -R P -R 2 выходное напряжение можно регулировать в широком диапазоне значений по формуле:
Вы можете быстро спроектировать схему, используя представленный здесь метод. NV
Что такое делитель напряжения потенциометра?
Введение
Потенциометр — это трехконтактный резистор со скользящим или вращающимся контактом.Это регулируемый делитель напряжения с двумя статическими контактами и одним подвижным контактом. Подвижный вывод представляет собой стеклоочиститель, который перемещается через элемент сопротивления, обычно по дуге, управляемой поворотной ручкой. Вращение ручки дает логометрическое деление потенциала на резистивном элементе. Потенциометр обычно используется в динамиках и ресиверах для регулировки громкости. Кроме того, он не может напрямую управлять двигателем, потому что его мощность слишком мала. Когда потенциометр действует как делитель напряжения, абсолютное сопротивление потенциометра не влияет на выходное напряжение, а его выходное напряжение пропорционально входному напряжению.
Рисунок 1. Структура потенциометра
Каталог
Ⅰ Подключение потенциометра
Потенциометр можно использовать как трехконтактный компонент или двухконтактный компонент . Последний можно рассматривать как реостат. Для обычного потенциометра (три контакта) ползунок рядом с центром представляет собой провод сопротивления. Два контакта на обоих концах провода сопротивления подключены к входу и заземлению (некоторые не подключены) соответственно.То есть один вывод подключен к входному сигналу, а другой вывод заземлен. В это время провод сопротивления имеет общее значение сопротивления на двух участках. Вы перемещаете скользящую деталь, чтобы пройти через этот провод сопротивления, чтобы получить переменное сопротивление. Если входные и выходные сигналы меняются местами, направление скольжения ползуна противоположно изменению сопротивления.
Как подключить потенциометр
1) Для потенциометра (или подстроечного резистора) с традиционными выводами (три контакта) сопротивление на обоих концах является фиксированным, а сопротивление среднего вывода — переменным.То есть клеммы с обеих сторон потенциометра — это полное сопротивление, а середина меняется. Например, источник питания подключается от любого одного контакта на сторонах резистора и выводится от среднего контакта, а напряжение изменяется при вращении среднего контакта.
Рисунок 2. Выход делителя напряжения потенциометра
2) Хотя сопротивление может изменяться в зависимости от ползунка, общее значение сопротивления контактов является фиксированным. В это время потенциометр приравнивается к регулятору тока, и выбранные выходные клеммы тока должны быть скользящей клеммой.Обычно используемые потенциометры имеют низкую точность измерения сопротивления и низкий температурный коэффициент, но до тех пор, пока сопротивление потенциометра одинаково, значение выходного напряжения остается неизменным.
Рисунок 3. Потенциометр как делитель напряжения
3) Если потенциометр используется в качестве переменного делителя напряжения, один контакт подключается к входному напряжению, средний контакт подключается к выходному напряжению, а другой контакт может быть заземлен. Когда вращающаяся ручка или скользящая ручка потенциометра срабатывают, подвижный контакт скользит по резистору.В это время выходное напряжение имеет определенную взаимосвязь с внешним напряжением, углом стеклоочистителя и ходом хода.
4) Если потенциометр используется в качестве переменного резистора, один конец подключается к входному напряжению, средний конец подключается к выходу, а другой конец может быть подвешен или подключен к среднему концу для получения плавного и непрерывно меняющегося значения сопротивления. .
Рисунок 4. Потенциометр, подключенный как переменный резистор
Как упоминалось выше, потенциометр может быть подключен как переменный резистор. Если вы хотите получить дополнительную информацию, вы можете получить ее из Различия между потенциометром и регулируемым резистором .
Ⅱ Описание символов и схем потенциометра
Имя | Символ потенциометра | Описание |
Нормальный потенциометр | Используйте RP (резистивный потенциометр) для обозначения потенциометра.Символом на рисунке обозначены 3 контакта потенциометра, обозначающие контакты микросхемы. | |
Переключатель потенциометра | S1 — это переключатель, прикрепленный к RP, а S1 управляется поворотной ручкой RP. Когда вы начинаете поворачивать ручку, после того, как переключатель замыкается, эта схема такая же, как у обычного потенциометра. Этот вид потенциометра в основном используется в цепях регулировки громкости с переключателями питания. | |
Как переменный резистор | Потенциометр на данный момент можно рассматривать как переменный резистор. | |
Потенциометр с двойным портом | Разделите 3 контакта потенциометра на 4 конца, чтобы сформировать двухпортовую схему.То есть клеммы 1 и 2 входных сигналов, клеммы 3 и 4 выходных сигналов, а клеммы 2 и 4 являются общими клеммами, которые обычно подключаются к заземлению линии. | |
Двухканальные потенциометры | Он имеет два символа цепи одинарного потенциометра, которые соединены пунктирной линией, чтобы указать, что сопротивления двойного потенциометра регулируются одновременно, то есть их значения сопротивления увеличиваются или уменьшаются одновременно. | |
Полулинейный ход | Это специальный двойной потенциометр. Два хода хода потенциометра синхронизированы, но их сопротивление изменяется во время регулировки. Только один механический ход такого потенциометра изменяет сопротивление, а значение сопротивления серебряной зоны равно нулю другой. Серебряная зона без сопротивления обозначается штриховкой в символе цепи.Когда подвижный контакт скользит вверх от середины, подвижный элемент RP-1 войдет в серебряную зону, а RP-2 войдет в область варистора; когда подвижная ручка опускается из среднего положения, RP-2 войдет в серебряную зону, а RP-1 войдет в зону варистора. Этот специальный потенциометр можно использовать в цепи контроллера стереобаланса (цепь управления в стереооборудовании). | |
с центральным краном | У него на один вывод больше, чем у обычного потенциометра, то есть ответного штифта.Отводной штифт устанавливается на среднее сопротивление потенциометра, а сопротивление между отводом и двумя неподвижными контактами одинаковое. Также существуют потенциометры, у которых отводы не установлены в среднее положение. |
Рисунок 5. Цепи потенциометра
Ⅲ Основы схемы делителя напряжения потенциометра
1) Резистор потенциометра в основном изготовлен из поликарбонатной синтетической смолы. Следует избегать следующих продуктов: аммиак, другие амины, водные растворы щелочей, ароматические углеводороды, кетоны, липидные углеводороды, сильнодействующие химические вещества (избыточный pH) и т. Д., в противном случае это повлияет на работу потенциометра.
2) При пайке клемм потенциометра избегайте использования емкостного флюса, который может вызвать окисление металла и образование плесени. При использовании флюса плохого качества плохая пайка может вызвать проблемы при пайке, что приведет к плохому контакту или обрыву цепи.
3) Если температура пайки клеммы слишком высока или время пайки слишком велико, это может привести к повреждению потенциометра. Температурный диапазон съемного потенциометра составляет 235 ℃ ± 5 ℃; Тип соединения проводов составляет 350 ℃ ± 10 ℃, а точка пайки должна быть больше 1.5 мм от корпуса потенциометра. Кроме того, избегайте сильного давления на клеммы, иначе это может привести к плохому контакту.
4) Во время пайки высоту флюса, попадающего на плату печатной машины, следует отрегулировать должным образом, и следует избегать его воздействия на потенциометр. Потому что это вызовет плохой контакт между щеткой и резистором или приведет к шуму.
5) Потенциометр лучше в структуре регулировки напряжения.
6) Избегайте образования конденсата или капель воды на поверхности потенциометра и избегайте использования потенциометра во влажном месте, чтобы предотвратить повреждение изоляции или короткое замыкание.
7) При фиксации винтов поворотного потенциометра усилие не должно быть слишком большим, чтобы избежать плохого вращения. Для потенциометра прямого скольжения избегайте использования слишком длинных винтов, в противном случае это может затруднить движение скользящей ручки и даже повредить сам потенциометр.
8) В процессе установки потенциометра на ручку толкающее усилие не должно быть слишком большим (не превышать показатель параметра номинального толкающего и тянущего усилия), в противном случае это может привести к повреждению потенциометра.
9) Сила вращения потенциометра будет уменьшаться при повышении температуры и уменьшаться при понижении температуры. Если потенциометр используется в низкотемпературной среде, ему необходима специальная низкотемпературная смазка.
Рисунок 6. Подключение цепи делителя напряжения потенциометра
10) Если вал или скользящая рукоятка потенциометра слишком длинная, их легко трясти, что приведет к нестабильности сигнала цепи.
11) Углеродная пленка потенциометра выдерживает температуру окружающей среды 70 ℃, и ее функция может быть потеряна при температуре выше 70 ℃.
12) Для регулируемого потенциометра, когда постоянный ток проходит через подвижный контакт, может возникнуть проблема анодного окисления. В этом случае лучше всего соединить компонент с отрицательным концом, а подвижный контакт — с положительным концом.
13) Ток нагрузки регулируемого потенциометра не может быть увеличен произвольно для обеспечения безопасности цепи. Фактическое измерение тока заключалось бы в подключении амперметра последовательно с потенциометром в активной цепи.
14) Не превышайте номинальную мощность при использовании регулируемого потенциометра.Например, когда рассеиваемая мощность превышает номинальное значение, это приведет к перегреву потенциометра.
15) Потенциометр является чувствительным, если он способен измерять очень малую разность потенциалов, и показывает значительное изменение длины балансировки при небольшом изменении измеряемой разности потенциалов.
16) Потенциометр постоянного тока создается путем падения напряжения на последовательно включенных резисторах. Разные резисторы будут давать разные значения. В потенциометре переменного тока можно использовать резисторы или даже катушки индуктивности или конденсаторы в качестве импедансов, которые будут снижать напряжение и обеспечивать напряжение, меньшее, чем приложенное напряжение.
17) Если расположить стеклоочиститель потенциометра в центре резистивного элемента, то напряжение на стеклоочистителе составляет 50%; если стеклоочиститель расположен на 1/4 расстояния от отрицательного узла, тогда напряжение стеклоочистителя составляет 1/4 всего напряжения.
18) Номенклатура потенциометров: Обычно используется метод прямой маркировки. Буквы и числа нанесены на корпус потенциометра, чтобы указать их модель, номинальную мощность, сопротивление и соотношение между сопротивлением и углом поворота.
Если у вас есть интерес, при более глубоком чтении, вы можете получить дополнительную информацию из Что такое основной делитель напряжения и правила.
Ⅳ Измерение сопротивления потенциометра
Основные требования для проверки потенциометра:
① Значение сопротивления соответствует требованиям схемы.
② Соединение между центральным скользящим концом и резистором хорошее, вращение плавное. Для потенциометра с переключателями действие переключателя должно быть точным, надежным и гибким.
Следовательно, перед использованием необходимо проверить работоспособность потенциометра.
1) Измерение сопротивления: Сначала выберите соответствующую передачу мультиметра в соответствии с сопротивлением измеренного потенциометра.Соответствует ли сопротивление между двумя концами переменного тока номинальному сопротивлению. Поверните скользящий контакт, и его значение должно быть зафиксировано. Если сопротивление показывает бесконечность, потенциометр поврежден.
2) Затем измерьте контакт между центральным концом и резистором, то есть сопротивление между двумя концами BC. Метод состоит в том, чтобы установить диапазон сопротивления мультиметра в соответствующем диапазоне. Во время измерения медленно вращайте вал и наблюдайте за показаниями мультиметра.Обычно показания постоянно меняются в одном направлении. Если есть скачок, падение или блокировка, значит, подвижный контакт неисправен.
3) Когда центральный конец скользит к головке или концу, значение сопротивления центрального конца и совпадающего конца равно 0 для идеального состояния. При фактическом измерении будет определенное значение (обычно определяемое номинальным значением, обычно менее 5 Ом), что является нормальным.
Часто задаваемые вопросы о делителе напряжения потенциометра
1.Как можно использовать потенциометр в качестве делителя напряжения?
Потенциометры могут использоваться как делители напряжения. Чтобы использовать потенциометр в качестве делителя напряжения, необходимо подключить все три контакта. Один из внешних контактов подключен к GND, другой — к Vcc, а средний контакт — это выход напряжения. В основном делитель напряжения используется для превращения большого напряжения в меньшее.
2. Как потенциометр влияет на напряжение?
Когда сопротивление потенциометра уменьшается (стеклоочиститель движется вниз), выходное напряжение с контакта 2 уменьшается, вызывая меньшее падение напряжения на R2.Аналогичным образом, когда сопротивление потенциометра увеличивается (дворник перемещается вверх), выходное напряжение с контакта 2 увеличивается, вызывая большее падение напряжения.
3. Что такое потенциометр с двумя бандажами?
Это означает, что два потенциометра объединены на одном валу, что позволяет параллельную настройку двух каналов. Наиболее распространены однооборотные потенциометры с одинаковым сопротивлением и конусом.
4. Сколько вольт может выдержать потенциометр?
100 вольт
Если потенциометр рассчитан на 1 ватт, вы можете подавать максимум 100 вольт.То есть 10 мА. Это относилось к напряжению на всех 10000 Ом. Это также означает, что вы не можете пропускать более 10 мА в Wiper.
Альтернативные модели
| Часть | Сравнить | Производителей | Категория | Описание | |
| Производитель.Номер детали: FM18W08-PG | Сравнить: Текущая часть | Производители: Cypress Semiconductor | Категория: Чип памяти | Описание: NVRAM FRAM Параллельный 256 Кбит 3.3V 28Pin PDIP | |
| Производитель № детали: FM25V05-G | Сравнить: FM18W08-PG VS FM25V05-G | Производители: Cypress Semiconductor | Категория: Чип памяти | Описание: FRAM 512Kbit Serial-SPI 3V / 3.Трубка SOIC, 3 В, 8 контактов, | |
| Номер детали производителя: FM25V05-GTR | Сравнить: FM18W08-PG VS FM25V05-GTR | Производители: Cypress Semiconductor | Категория: Чип памяти | Описание: FRAM 512Kbit Serial-SPI 3V / 3.3 В 8 контактов SOIC T / R | |
| Производитель Номер детали: FM1808-70-PG | Сравнить: FM18W08-PG VS FM1808-70-PG | Производитель: Ramtron | Категория: Чип памяти | Описание: Схема памяти, 32KX8, CMOS, PDIP28, GREEN, MS-011, DIP-28 |
L8: Переменные резисторы — Физические вычисления
Содержание
- Типы переменных резисторов
- Потенциометры
- Как работает потенциометр?
- Типы потенциометров
- Внутри потенциометра
- Ручки потенциометров
- Создание настраиваемых ручек для 3D-печати
- Потенциометры как аналоговые джойстики
- Потенциометры как делители напряжения
- Использование потенциометра как двухполюсного переменного резистора
- Упражнение: Построить светодиодную схему с потенциометром в качестве переменного резистора
- Схема прототипа в Tinkercad Circuits
- Схема прототипа на макетной плате
- Упражнение: Заменить другой переменный резистор
- Схема силового резистора
- Схема светозависимого резистора
- Упражнение: создайте свой собственный переменный резистор своими руками
- Пример поворотного потенциометра «сделай сам»
- Пример ползункового потенциометра «сделай сам»
- Самодельная низкоуровневая электроника
- Ресурсы
В предыдущих уроках мы использовали Работает с резисторами фиксированного номинала.В этом уроке мы узнаем о переменных резисторах — резисторах, которые изменяют свое сопротивление в зависимости от какого-либо физического входа (например, потенциометры) или воздействия окружающей среды, такого как термисторы (температура), чувствительные к силе резисторы (сила) или фоточувствительные резисторы (световые). Ниже мы привели несколько примеров.
Рисунок. Многие распространенные датчики на самом деле представляют собой переменные резисторы — они динамически изменяют свое сопротивление в ответ на воздействие человека или окружающей среды.Например, термисторы изменяют свое сопротивление в зависимости от температуры, фотоэлементы — на основе света, силочувствительные резисторы (FSR) — на основе силы. Фактически, в ваших наборах оборудования есть термисторы, фотоэлементы и FSR! Цены и изображения взяты с сайта Sparkfun.com; запчасти часто могут быть дешевле оптом от таких поставщиков, как Digi-Key или Mouser Electronics.
Это интересно! Физические вычисления — это все о взаимодействиях, и резистивные материалы, которые реагируют на различные стимулы, открывают новый мир возможностей!
Типы переменных резисторов
Существуют двухполюсных переменных резисторов (или «двухполюсных» или «двухпроводных»), таких как реостаты, фотоэлементы и силочувствительные резисторы, а также трехполюсных переменных резисторов , которые называются потенциометрами.Оба типа не зависят от ориентации — как и обычные резисторы, они будут работать в любом направлении (неполяризованном). См. Схематические обозначения ниже.
Рисунок. Схематические обозначения некоторых примеров двух- и трехполюсных переменных резисторов. Обратите внимание на то, что некоторые схематические символы совпадают с для разных типов переменного резистора.
Независимо от типа, все переменные резисторы имеют схематический символ, аналогичный обычному резистору, но с некоторыми визуальными изменениями, указывающими на «изменчивость».Несколько общих замечаний:
- Схема двухполюсного переменного резистора очень похожа на обычный резистор, но имеет диагональную линию , через которую проходит , указывающая на изменчивость.
- Потенциометры имеют три ножки, которые также представлены на схематический. Средняя стрелка («ножка стеклоочистителя») может быть подключена в электрическую цепь, и это будет фактически показано на принципиальной схеме. Мы увидим это ниже.
- Некоторые распространенные переменные резисторы, такие как светозависимые резисторы (LDR или фотоэлементы), имеют свои собственные условные обозначения .Другие, например, чувствительные к силе резисторы и реостаты, имеют тот же символ.
Потенциометры, вероятно, являются наиболее распространенным типом переменного резистора и важным компонентом, о котором нужно знать, так что приступим!
Потенциометры
Потенциометр (или потенциометр) — это трехконтактный резистор со скользящим или вращающимся контактом, который можно использовать для динамического изменения сопротивления.
Видео. На этой анимации показано, как стеклоочиститель можно использовать для изменения сопротивления поворотного потенциометра.Цифра справа — это формальный электрический символ. Анимация Джона Фрелиха. Создано в PowerPoint.
Потенциометры — это действительно повсеместные электронные компоненты, которые можно найти во всем, от регуляторов громкости до аналоговых джойстиков. На наших курсах UW мы часто предоставляем потенциометры 10 кОм в наших наборах, такие как потенциометр 10K для монтажа на панели и потенциометр подстройки 10K, показанные ниже.
Рисунок. Два примерных потенциометра, которые обычно входят в наши комплекты оборудования: панельный 10 кОм и подстроечный потенциометр 10 кОм.
Хотя потенциометры часто используются в качестве устройств ввода данных человеком, это не всегда так. Например, потенциометр можно использовать в цепи обратной связи для серводвигателя. Когда двигатель вращается, он также вращает диск управления встроенного потенциометра (стеклоочиститель), который передает информацию о вращении в схему управления (см. Главу 15.4 о RC-сервоприводах в Scherz and Monk, 2016).
Хотя до сих пор широко используется, некоторые области применения потенциометров были отнесены к цифровым элементам управления, таким как поворотные энкодеры и кнопки.Не запутайтесь: поворотные энкодеры могут выглядеть очень похоже на потенциометры — действительно, с прикрепленными ручками они могут выглядеть одинаково. Однако энкодеры не являются резистивными устройствами, требуют использования цифровых схем и могут вращаться непрерывно. Напротив, потенциометры являются резистивными компонентами, могут использоваться в аналоговых или цифровых схемах и обычно имеют регулируемый угол 200-270 °.
Как работает потенциометр?
Потенциометры имеют три ножки: сопротивление между двумя внешними ножками (ножка 1 и ножка 3) не меняется.Например, если вы используете потенциометр 10 кОм, то сопротивление между ножками 1 и 3 всегда будет 10 кОм независимо от положения стеклоочистителя (ножка 2). Если вы используете резистор 1 кОм, то сопротивление между ножками 1 и 3 будет 1 кОм и так далее.
Мощность потенциометра находится в той средней ножке (ножка 2), сопротивление которой изменяется в зависимости от положения скользящего или вращающегося контакта потенциометра (стеклоочистителя). Можно представить себе потенциометр как содержащий два взаимозависимых резистора \ (R_1 \) и \ (R_2 \), сумма которых всегда равна \ (R_ {Total} \) (где \ (R_ {Total} \) — это общее значение потенциометра. значение, такое как 1 кОм или 10 кОм).Когда вы перемещаете контакт ползунка, сопротивление \ (R_1 \) будет увеличиваться, а сопротивление \ (R_2 \) уменьшается. См. Анимацию ниже.
Видео. Анимация Джона Фрелиха. Создано в PowerPoint.
Типы потенциометров
Потенциометры бывают разных размеров, номинальной мощности и физических конструкций. Некоторые большие конструкции могут выдерживать мощность в несколько ватт (способную рассеивать много тепла), в то время как меньшие конструкции для поверхностного монтажа рассчитаны только на долю ватта (как и \ (\ frac {1} {4} \) ватт резисторы в ваших наборах).
Рисунок. Потенциометры — это повсеместные устройства ввода, которые можно найти во всем, от автомобилей до микшерных пультов. Существует почти бесконечное количество дизайнов, поэтому мы показываем только небольшой образец выше. Обратите внимание, что вы не можете определить значение сопротивления потенциометра (или потенциометра), просто взглянув на него, и вы не можете определить, является ли это конусом линейным или логарифмическим. Логарифмические потенциометры широко используются в аудиоприложениях (потому что человеческое ухо воспринимает громкость логарифмически). Источники изображений: изображения потенциометра с темным фоном взяты из Adafruit.Остальные из дигики.
Потенциометры различаются в основном по следующим параметрам:
Диапазон сопротивления . Как и резисторы, потенциометры предназначены для обеспечения разного сопротивления, но в определенном диапазоне (обычно 0–1 кОм и 0–10 кОм).
Линейный в сравнении с логарифмическими конусами (или дорожками). В линейных потенциометрах сопротивление изменяется линейно при перемещении дворника. В логарифмических потенциометрах сопротивление изменяется логарифмически.Последний тип распространен в звуковых приложениях, потому что человеческое ухо воспринимает величину звука логарифмически с большей чувствительностью для тихих звуков и меньшей для громких.
Рассеиваемая мощность . Опять же, как и резисторы, потенциометры имеют разные «номинальные мощности», которые соответствуют их способности рассеивать тепло. В этом техническом описании подстроечного потенциометра указано, что номинальная мощность составляет 0,5 Вт, в то время как этот потенциометр для монтажа на панели рассчитан на 0,1-0,2 Вт (см. Техническое описание).
Поворотный по сравнению с ползунком . Поворотные потенциометры используют вращающуюся ручку для управления ножкой стеклоочистителя, в то время как ползунковые потенциометры используют ползунок.
Крепление . Некоторые потенциометры предназначены для «монтажа», например, на приборной панели автомобиля или микшерной панели. Другие предназначены для макетирования или для монтажа на печатных платах (так называемые потенциометры «поверхностного монтажа»).
Ручка .Для потенциометров, используемых для ввода данных человеком, существует множество типов ручек для обеспечения эргономичного и удобного взаимодействия.
Внутри потенциометра
Если вам интересно, как устроен потенциометр, это видео Джона Купера демонстрирует прекрасную деконструкцию поворотных потенциометров и то, как они работают.
Видео. Видео-деконструкция потенциометров и их работы от Джона Купера (на YouTube).
Ручки потенциометров
Скорее всего, вы много раз взаимодействовали с потенциометрами в своей жизни; однако они закрыты ручками, которые делают потенциометр более эргономичным и удобным.
Существует большое разнообразие ручек, которые подходят как для потенциометров, устанавливаемых на панели, так и для поворотных энкодеров, используемых в различных приложениях, ориентированных на пользователя, таких как аудиомикшеры, джойстики и панели управления. Взгляните на несколько примеров ниже:
Рисунок. Небольшой образец регуляторов потенциометра и поворотного энкодера. Все изображения от Adafruit. Слева направо: Soft Touch T18 — белый, Soft Touch T18 — красный, тонкая металлическая ручка, механически обработанная металлическая ручка, выдвижной горшок с пластиковой ручкой
Создание пользовательских ручек для 3D-печати
Веселое вводное упражнение по 3D-печати чтобы спроектировать, смоделировать и напечатать собственную ручку потенциометра. Обычно мы делаем это в начале модуля изготовления в нашем курсе физических вычислений. Вот несколько простых примеров разработанных нами ручек потенциометров для 3D-печати.
Рисунок. Три простых ручки потенциометра, созданные в Fusion 360 (по 5-10 минут каждая). Для печати чертежей САПР на 3D-принтере Ultimaker 2+ с высотой слоя 0,2 мм и без опор или прилипания пластин (, например, полей) требуется примерно 20 минут. Все дизайны выполнены Джоном Фрелихом. Вы можете увидеть пошаговые обучающие видео здесь и здесь.
Еще больше удовольствия — комбинировать пользовательские 3D-отпечатки с микроконтроллером и создавать пользовательские приложения, которые создают новые интерактивные возможности.
Видео. Короткое видео, демонстрирующее, как пользовательские 3D-печатные ручки потенциометра используются в качестве пользовательских игровых контроллеров с Arduino Leonardo и пользовательскими эскизами обработки. Код для Arduino + Processing «Etch-a-sketch» находится здесь, а код для Arduino + Processing «Pong» здесь. Все 3D-проекты САПР и код выполнены Джоном Фрелихом.
Потенциометры как аналоговые джойстики
Как и намекают наши 3D-печатные конструкции, потенциометры как игровые контроллеры имеют долгую историю. В наши комплекты оборудования мы часто включаем 2-осевой джойстик, подобный этому от Parallax (6 долларов.95 на Adafruit), который содержит два встроенных потенциометра 10 кОм.
Рисунок. В 2-осевом джойстике Parallax есть два встроенных потенциометра 10 кОм, по одному для каждой оси. Вы можете посмотреть видео-демонстрацию здесь.
Перемещая аналоговый джойстик, вы независимо управляете двумя потенциометрами в конфигурации делителя напряжения. Есть \ (V_ {Out} \) для потенциометра «вверх / вниз» и \ (V_ {Out} \) для потенциометра «влево / вправо». См. Принципиальную схему выше.
Видео. Короткий отрывок из этого официального видео о Parallax, показывающий, как физическое движение джойстика преобразуется в электрический сигнал с помощью двух потенциометров.
Потенциометры как делители напряжения
Потенциометры на самом деле представляют собой удобно упакованные делители напряжения, которые мы впервые описали в Уроке 3: \ (R_ {1} \) и \ (R_ {2} \) делят напряжение при перемещении дворника потенциометра.
Рисунок. А — это компактный делитель напряжения. Изображение сделано в PowerPoint.
В качестве примера давайте подключим потенциометр к 5 В (ножка 1) и заземлению (ножка 3) и посмотрим, как выходное напряжение \ (V_ {out} \) изменяется на ножке стеклоочистителя (сигнал на ножке 2):
Рисунок. Давайте подключим потенциометр к 5 В и заземлению. Изображение сделано в PowerPoint.
Теперь посмотрим, что происходит, когда мы меняем дворник. Обратите внимание, как \ (V_ {out} \) изменяется согласно \ (V_ {in} * \ frac {R2} {(R1 + R2)} \). На видео ниже мы используем потенциометр 1 кОм, но функция та же.
Видео. Демонстрация того, как \ (V_ {out} \) изменяется согласно \ (V_ {in} * \ frac {R2} {(R1 + R2)} \). Анимация сделана в PowerPoint и CircuitJS.
Использование потенциометра в качестве двухполюсного переменного резистора
Когда используются только две клеммы (или ножки) потенциометра — внешняя ножка и ножка стеклоочистителя (или сигнальная ножка), потенциометр действует как реостат или два -клемма переменного резистора . В этой конфигурации вы можете использовать потенциометр для изменения сопротивления в вашей цепи, а не в качестве делителя напряжения.Собственно, этим мы и займемся ниже. Мы вернемся к использованию потенциометра в качестве делителя напряжения, когда начнем работать с микроконтроллерами.
Упражнение: Постройте схему светодиода с потенциометром в качестве переменного резистора
Уф, теперь мы готовы создавать вещи! Давайте начнем с создания простой светодиодной схемы с нашим потенциометром в качестве двухполюсного переменного резистора. Здесь мы будем использовать только одну внешнюю ножку (либо ножку 1, либо ножку 3, не имеет значения) и сигнальную ножку (ножку 2). Давайте взглянем на принципиальную схему — это то, что вы ожидали? Почему или почему нет?
Рисунок. Пример подключения потенциометра в качестве переменного резистора. Изображение сделано в Fritzing и PowerPoint.
Вы заметили в нашей схеме дополнительный резистор с фиксированным значением? Как вы думаете, почему это у нас есть?
Ответ: поскольку многие потенциометры переходят от 0 Ом к своему максимальному значению, мы должны использовать «резервный» резистор в серии с нашим потенциометром. В противном случае, когда мы поворачиваем потенциометр до низких значений сопротивления, через наш светодиод будет проходить слишком большой ток. Например, с типичным красным светодиодом с \ (V_f = 2V \) и батареей 9V, если мы установим потенциометр на 50 Ом, то у нас будет \ (I = \ frac {7V} {50Ω} = 140mA \), что намного превышает порог 20-30 мА светодиода.
Видео. Вот пример того, что произошло бы, если бы вы повернули потенциометр до низкого сопротивления без резервного резистора. Бум, еще один перегоревший светодиод. Видео сделано с помощью Tinkercad и Camtasia.
Конечно, вы также можете построить схему на основе потенциометра в CircuitJS, подобную этой.
Прототип схемы в Tinkercad Circuits
Мы хотели бы, чтобы вы прототипировали две светодиодные схемы на основе потенциометра в Tinkercad Circuits: первая без макетной платы и вторая с макетной платой.При желании можно включить амперметр и вольтметр, показывающие, как изменяются падение тока и напряжения при вращении ручки потенциометра. Вот два возможных примера светодиодной схемы на основе потенциометра. Убедитесь, что и графические изображения, и принципиальные схемы имеют смысл. Помните, что мы используем только два из трех ножек потенциометра.
Рисунок. Пример подключения потенциометра в качестве переменного резистора к макетной плате.Существует множество других возможных функционально эквивалентных схем. Изображение сделано в Fritzing и PowerPoint.
Для обеих схем Tinkercad включите снимок экрана в свои журналы прототипов и опишите свои наблюдения (достаточно одного или двух предложений).
Прототип схемы на макетной плате
После того, как вы построили и смоделировали схемы в Tinkercad, мы хотели бы, чтобы вы физически построили версию в панировке с вашими аппаратными комплектами. Сделайте фото и быстрое демонстрационное видео работы схемы и поместите их в свои журналы прототипирования.Опишите любые проблемы.
Видео. Вот один из возможных способов смонтировать схему подстроечного потенциометра с резервным резистором и красным светодиодом. Что вы сделали? Сделайте похожее видео для своих журналов по прототипированию.
Упражнение: Поменяйте местами другой переменный резистор
После того, как вы закончите описанное выше, мы хотели бы, чтобы вы поигрались и поэкспериментировали с другими переменными резисторами в ваших аппаратных комплектах, включая термистор (в коробке Plusivo), светильник -зависимый резистор (также в вашей коробке Plusivo), ползунковый потенциометр и / или мой любимый, чувствительный к усилию резистор .
Выберите два из них и поменяйте их местами вместо подстроечного потенциометра на макетной плате. Сделайте несколько фотографий, видео-демонстрацию и напишите краткое описание того, что вы наблюдали / узнали, для своих журналов по прототипированию.
Ниже приведены два примера.
Схема силового резистора
Силочувствительный резистор (FSR) реагирует на силу или давление. По мере увеличения приложенной силы сопротивление на двух выводах уменьшается. В приведенной ниже простой схеме светодиод будет получать больше тока (и в результате излучать больше света) по мере того, как к FSR прикладывается большее давление.
Рисунок. Пример подключения силового резистора к простой светодиодной цепи. Изображение сделано в Fritzing и PowerPoint.
Вот демонстрация видео:
Видео. Видео демонстрация светодиодной схемы на основе FSR.
Схема светозависимого резистора
Светозависимый резистор (LDR) — иногда называемый фотоэлементом или фоточувствительным резистором — снижает свое сопротивление в ответ на свет. В простой схеме ниже вы заметите, что красный светодиод ярко загорается в ответ на фонарик.Часто мы хотим прямо противоположного поведения: яркость светодиода обратно пропорциональна свету.
Рисунок. Пример схемы светозависимого резистора (LDR) со светодиодом. В этой конфигурации яркость светодиода будет увеличиваться пропорционально количеству света, падающего на датчик LDR. Изображение сделано в Fritzing и PowerPoint.
И демонстрация видео:
Видео. Видео демонстрация схемы светодиода на основе LDR.
Задание: создайте свой собственный переменный резистор своими руками
В завершение мы хотели бы, чтобы вы создали свой собственный переменный резистор своими руками.Мы включили графитовые карандаши 12B в ваши комплекты оборудования именно для этой цели, но вы можете использовать другие материалы, если захотите.
Грифели для карандашей представляют собой смесь глины и графита — чем больше графита, тем выше проводимость. Чем больше графита, тем выше рейтинг B (вы можете получить карандаши 1B, 2B, 3B… 14B). Для ваших комплектов у нас есть 12В.
Это задание вдохновлено Джеффом Феддерсеном из программы ITP Нью-Йоркского университета. Пожалуйста, посмотрите это видео, прежде чем продолжить (это одно из моих любимых!).
Ом Часть 2 от Джеффа Феддерсена на Vimeo.
Для журнала прототипирования нарисуйте принципиальную схему потенциометра DIY, физически соберите его, а затем сделайте несколько фотографий и видео, демонстрирующих, как он работает. Также включите краткое описание и отражение того, что вы узнали.
Пример поворотного потенциометра «сделай сам»
Вот пример поворотного потенциометра «сделай сам», который я сделал из картона, бумаги, канцелярской скрепки и кнопки (для стеклоочистителя), а также карандашный набросок 12В (для резистивного материала).
Видео. Поворотный потенциометр lo-fi, сделанный из картона, бумаги, канцелярской скрепки и канцелярской кнопки (для стеклоочистителя), а также карандашный набросок 12B (для резистивного материала).
Пример потенциометра-ползунка своими руками
Вот пример потенциометра-ползунка своими руками, который я сделал из аналогичных материалов: картон, бумага, картонный стеклоочиститель с медной лентой и карандашный набросок 12B (для резистивной дорожки).
Видео. Потенциометр ползунка lo-fi, сделанный из картона, бумаги, картона, обернутого медной лентой (для ползунка), и карандашного наброска 12B (для резистивной дорожки).
DIY lo-fi electronics
Есть много отличных ресурсов для создания lo-fi датчиков, кнопок и разъемов с использованием повседневных материалов для поделок, таких как фольга, картон и скрепки. Ознакомьтесь с этими ресурсами, чтобы начать мозговой штурм!
Ресурсы
Глава 8, Переменные резисторы, Hughes, Практическая электроника: компоненты и методы , O’Reilly Media, 2015
Глава 11: Потенциометр в Platt, Марка: Энциклопедия электронных компонентов Том 1 : Резисторы, конденсаторы, индукторы, переключатели, энкодеры, реле, транзисторы , O’Reilly, 2012.
Все материалы имеют открытый исходный код и созданы лабораторией Makeability Lab и профессором Джоном Э. Фрёлихом. Нашли ошибку? Отправьте сообщение о проблеме на GitHub.
Делители напряжения
Делители напряжения Главная | Карта | Проекты | Строительство | Пайка | Исследование | Компоненты | 555 | Символы | FAQ | СсылкиИх также называют разделителями потенциала.
Следующая страница: Транзисторные схемы
См. Также: Преобразователи |
Напряжение и ток | Сопротивление |
Импеданс
Делитель напряжения (делитель потенциала)
|
- Если R2 намного меньше , чем R1, Vo мало (низкий, почти 0 В)
(поскольку большая часть напряжения проходит через R1) - Если R2 примерно такое же , что и R1, Vo составляет примерно половину против
(поскольку напряжение распределяется примерно поровну между R1 и R2) - Если R2 намного больше , чем R1, Vo большое (высокое, почти Vs)
(поскольку большая часть напряжения проходит через R2)
Делители напряжения также называются делители потенциала , название который происходит от разности потенциалов (собственное название напряжения).
Одно из основных применений делителей напряжения — подключение
ввод преобразователей в цепи …
Использование входного преобразователя (датчика) в делителе напряжения
Большинство входных преобразователей (датчиков) изменяют свое сопротивление и обычно напряжение делитель используется для преобразования его в переменное напряжение , что более полезно. Сигнал напряжения может быть подан на другие части схемы, например, вход в микросхему или транзисторный ключ.Датчик — это одно из сопротивлений в делителе напряжения. Может быть вверху (R1) или внизу (R2), выбор определяется тем, когда требуется большое значение для выходного напряжения Vo:
- Поместите датчик в верхнюю часть (R1), если вы хотите большой Vo , когда датчик имеет малое сопротивление .
- Поместите датчик в нижнюю часть (R2), если вы хотите большой Vo , когда датчик имеет большое сопротивление .
Выбор номинала резистора
| ИЛИ |
Вы можете использовать мультиметр, чтобы помочь вам найти минимальное и максимальное значения сопротивления датчика (Rmin и Rmax). Не нужно быть точным, подойдут приблизительные значения.
Затем выберите номинал резистора: R = квадратный корень из (Rmin × Rmax)
Выберите стандартное значение, близкое к рассчитанному.
Например:
LDR: Rmin = 100,
Rmax = 1M,
поэтому R = квадратный корень из (100 × 1M)
= 10к.
замена резистора и датчика
Резистор и датчик можно поменять местами, чтобы инвертировать действие делителя напряжения. Например, LDR имеет высокое сопротивление в темноте и низкое сопротивление в темноте. ярко освещенный, так что:- Если LDR находится наверху (около + Vs) ,
Vo будет низкой в темноте и высокой при ярком свете . - Если LDR находится внизу (около 0 В) ,
Vo будет высотой в темноте и низкой при ярком свете .
Использование переменного резистора
| Датчик и переменный резистор можно поменять местами при необходимости |
Значение переменного резистора должно быть больше, чем номинальное значение постоянного резистора. Для более точного управления вы можете использовать постоянный резистор последовательно с переменный резистор. Например, если 10 тыс. фиксированный резистор подходит, вы можете заменить его фиксированным Бег 4,7 км резистор последовательно с 10 тыс. переменный резистор, позволяющий регулировать сопротивление от От 4,7 до 14,7 км.
Если вы планируете использовать переменный резистор, подключенный между питанием + Vs
и базу транзистора вы должны включить резистор последовательно с переменной
резистор.Это сделано для предотвращения разрушения транзистора чрезмерным базовым током при
переменный резистор уменьшен до нуля. Для получения дополнительной информации см.
страницу о транзисторных схемах.
Следующая страница: Транзисторные схемы | Изучение электроники
© Джон Хьюс 2007, Клуб электроники, www.kpsec.freeuk.com
Этот сайт был взломан с использованием ПРОБНОЙ версии WebWhacker. Это сообщение не появляется на лицензированной копии WebWhacker.
Неизвестные факты о переменном резисторе в деталях
Что такое переменный резистор?
Переменный резистор — это электронный компонент. он происходит из семейства резисторов . Резистор — это устройство, которое контролирует количество тока, протекающего через него, и, следовательно, электрическую / электронную схему, в которой он подключен. И свойство резистора сопротивления отвечает за ток, протекающий через него.
Резисторы изготавливаются с фиксированным номиналом резистора или переменным сопротивлением Ом (Ом).Значение такого резистора находится в диапазоне от 0 Ом до нескольких M Ом (мегаом)
Переменный резистор может быть определен как резистор, значение которого может быть изменено / отрегулировано в соответствии с требованиями в данном пример.
На изображениях ниже показан символ переменного резистора как в стандарте
IEC , так и в американском стандарте , а также реальная практическая фотография переменного резистора:Конструкция и работа переменного сопротивления:
Переменный резистор обычно состоит из резистивной дорожки и контакта стеклоочистителя (касающийся провод).Провод стеклоочистителя перемещается по резистивной дорожке при повороте ручки стеклоочистителя. В основном винтовая структура присутствует в ручке стеклоочистителя для поворота ручки. (См. Изображения ниже)
Вращение ручки приводит к изменению сопротивления. Примерно посередине между двумя выводами находится половина значения сопротивления номинального значения сопротивления, напечатанного на базе переменного резистора.
Давайте посмотрим на конструктивную схему переменного резистора:
1,2,3 — три названия клемм.
Причиной этого является резистивная дорожка, резистивная дорожка предназначена для обеспечения сопротивления на единицу длины (Ом / мм).
Лаборатории калибруют механическое движение ручки для получения заданных значений сопротивления.
Эта резистивная дорожка состоит из углеродных соединений, сплава вольфрама и смеси никель-хром (для резистивного электролизера).
Как правило, резистивная дорожка, состоящая из тонких резистивных проволочных обмоток , используется для достижения более высокой точности приложений, где небольшое изменение сопротивления очень важно.
Вся система печатной резистивной дорожки и стеклоочистителя собрана в корпусе. Другими словами, он изолирован от внешнего прямого контакта, чтобы избежать контакта с человеком или другими схемами.
Однако, если мы используем все три вывода переменного резистора, то его эквивалентная схема представляет собой схему делителя напряжения, и выходное напряжение можно определить по следующей формуле:
Положение относительно значения сопротивления потенциометра:
Теперь определяем значение сопротивления теоретически, когда дворник находится в определенном положении на резистивной дорожке.
(Обратите внимание, что нижеприведенный метод работает для линейно распределенного сопротивления / отпечатков)
лет, длина дорожки = L см
сопротивление для единицы длины = x Ом / см
Следовательно, сопротивление поперек Клеммы 1 и 2 = L * x Ω (Ом)
(для этого нам понадобится мультиметр, поскольку резистивная дорожка круглая и ее длину трудно измерить нормально)
var.резистор:
1) В электронных схемах, где мы не знаем заранее номинал резистора, необходимого для схемы.
2) Это очень полезно для анализа поведения схемы при различных значениях сопротивления. Мы можем построить график зависимости входа от выхода, используя переменный резистор.
3) Братьями и сестрами переменного регистра являются Реостат, Предустановка, Потенциометр (сокращенно «горшок»).
Кроме того, мы можем клонировать поведение реостата и измерителя потенциала, используя переменный резистор, изменив клеммные соединения
4) В цепи управления звуком регулятора скорости вентилятора диммера и т. Д.для коммерческого использования.
5) Как схема делителя напряжения.
Вот список некоторых доступных значений переменного резистора:
Ex . 100 Ом, 1 кОм, 10 кОм, 100 кОм, 200 Ом, 2 кОм, 4,7 кОм, 47 кОм, 470 кОм и т.
