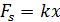Механическая работа — это… Что такое Механическая работа?
 Механическая работа |
| Работа силы |
| Ключевые статьи |
| См. также: Портал:Физика |
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы[1].
Определение
В механике можно ввести понятие работы, исходя из довольно простых представлений[2]
Работа силы (сил) над одной точкой
- Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения
Здесь точкой обозначено скалярное произведение[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:
- ,
где и — радиус-векторы начального и конечного положения тела соответственно.
- Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.
Работа силы (сил) над системой или неточечным телом
Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).
Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:
где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что
Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:
| . |
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике
В термодинамике работа, совершенная газом при расширении[8], рассчитывается как интеграл давления по объёму:
Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .
В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .
Таким образом, если обозначить эту работу буквой , то, в силу данного определения,
- ,
следовательно,
- (1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим
Единицей измерения работы в СИ является Джоуль, в СГС — эрг
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10−7 Дж
Ссылки
- ↑ Концепции современного естествознания
- ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
- работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
- работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
- работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
- работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
- работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).
- ↑ Механическая работа. Мощность
- ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература
- Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.
См. также
Работа в физике — это что такое?
Работа в физике — это величина, которую находят путем умножения модуля силы, перемещающей тело, на расстояние, на которое оно сдвинулось. В статье мы подробно рассмотрим ситуации, когда тело перемещается и остается неподвижным. Узнаем формулу работы и единицы ее измерения.
Силы, действующие на тело
Представим себе, что у нас есть нить, на которую подвешено тело. Со стороны нити на него действует сила упругости нити, обозначим ее F. Тело неподвижно, допустим, мы прикрепили нить к штативу. Нужно ли что-то делать, чтобы это состояние сохранялось сколь угодно долго? Нет. Хотя на тело действует сила, оно не двигается.
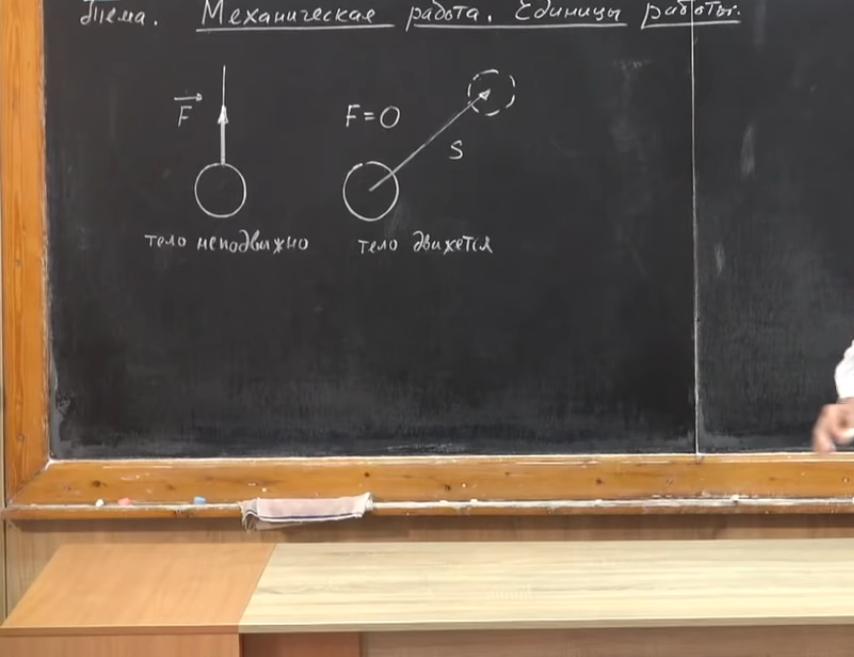
Работа в физике — это что такое? Прежде чем ответить на данный вопрос, рассмотрим ситуацию. Предположим, тело движется, но на него не действуют никакие силы. Например, если это шар в далеком космическом пространстве, вдали от всех звезд и галактик. Тогда сила их притяжения будет пренебрежимо мала. Изобразим схему.
Тело переместилось на некоторое расстояние s, но сила при этом отсутствует (F=0). Необходимо ли предпринимать какие-либо действия для того, чтобы тело продолжало двигаться? Нет. Это состояние может сохраняться сколь угодно долго. Это равномерное прямолинейное движение при отсутствии сил, действующих на тело.
Сила, производящая механическую работу
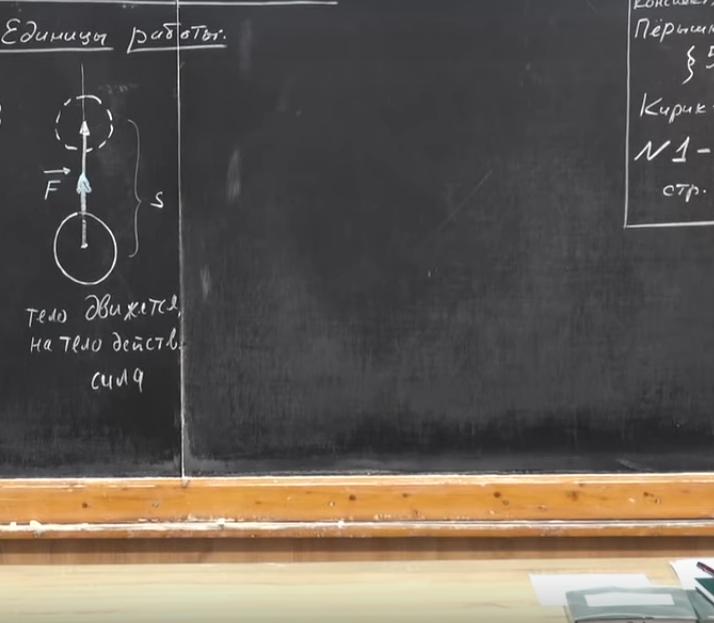
А теперь принципиально другая ситуация. Мы будем поднимать тот же шар. На него действует сила, она приложена к телу со стороны веревки. Величину перемещения шара обозначим буквой s, а силу — F. Будет ли шар сам подниматься? Нет, что-то должно его поднимать. Например, где-то должен работать электродвигатель. Но для того, чтобы он работал, с плотины должна падать вода, которая приводит к вращению турбины, к которой подключен генератор. По линии электропередач энергия должна передаваться в двигатель, а он — работать и поднимать груз. То есть перемещение не может реализоваться само по себе.
Физики говорят, что в первых двух случаях сила не выполняет никакой механической работы. В третьем случае работа выполняется. Чем она производится? Силой F. В физике работа — это величина. А раз так, то она может меняться в большую и меньшую сторону. Нетрудно догадаться, что если силу увеличить и перемещать тело на то же самое расстояние, то работа этой силы будет больше. Как можно увеличить силу? Например, взять шар в два раза тяжелее. Тогда работа увеличится вдвое. Следовательно, работа силы пропорциональна величине силы. Это закон.
Формула механической работы
Представим, что нам нужно поднять все тот же шар не на 50 см, а на 100 см. Необходимо совершить работу, чтобы поднять его сначала на первую половину дистанции, а затем на вторую. Всякий раз будет совершаться одинаковая работа, но общая работа будет в два раза больше. Значит, работа прямо пропорциональна расстоянию перемещения тела. Поэтому физики договорились обозначить величину F*s буквой А и назвать ее работой силы. Выражение F*s как раз и будет прямо пропорционально силе и перемещению тела.
A=F*s — это формула работы в физике. A — искомая величина силы, приложенной к телу, а s — путь, пройденный телом. Однако бывают ситуации, когда сила приложена к телу, а оно не перемещается. В нашем третьем случае тело перемещается в том же направлении, в котором приложена сила. Поэтому точнее будет сказать, что s — это перемещение тела в направлении действия силы. Сформулируем определение: работа в физике — это величина, равная произведению модуля силы на перемещение тела в направлении действия силы.
Единицы измерения
Посмотрим на определяющую формулу A=F*s. [А]=Н*м=Дж. Н — это ньютоны, Дж — джоули. Как понять, что из себя представляет 1 джоуль? Нарисуем схему, на которой изобразим силу, совершающую работу в один джоуль.
На рисунке показано первоначальное и конечное положение тела. Мы переместили его на расстояние 1 м. При перемещении к телу была приложена сила в один ньютон. А=1 Н*1 м=1 Дж. То есть один джоуль — это работа, совершаемая силой в один ньютон при перемещении тела, на расстоянии 1 м в направлении действия силы.
Один джоуль — это небольшая работа. Чтобы поднять килограммовую гирю на 10 см, нужно совершить работу в 1 джоуль. Чтобы поднять ее на метровую высоту, нужно совершить работу в 10 джоулей. Если говорить о работе подъемных кранов, то они поднимают тонны на десятки метров. Поэтому используют и другие единицы измерения работы: килоджоули, мегаджоули и т. д. 1 кДж=1000 Дж, 1 МДж=10^6 Дж. Стрелку настенных часов приводит в движения мотор. Он совершает работу, гораздо меньшую, чем один джоуль. Ее измеряют в милиджоулях. 1 мДж=0,001 Дж. Существуют и микроджоули. 1 мкДж=1*10^-6 Дж.
Конспект «Механическая работа. Механическая мощность»
«Механическая работа. Механическая мощность»
Код ОГЭ 1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность.
Работа силы – физическая величина, характеризующая результат действия силы.
Механическая работа А постоянной силы 
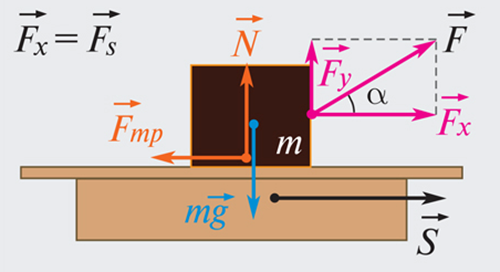
равна произведению модуля вектора силы на модуль вектора перемещения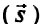 
и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а.
Единица измерения работы в СИ – джоуль: [А] = Дж = Н • м.
Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.
Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:
- сила действует, а тело не перемещается;
- тело перемещается, а сила равна нулю;
- угол между векторами силы и перемещения равен 90° (cos a = 0).
Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости.
Работа – скалярная величина, она может быть как положительной, так и отрицательной.
- Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
- Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.
Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.
Примеры расчёта работы отдельных сил:
Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела: A = mg(h1 – h2). По замкнутой траектории работа силы тяжести равна нулю.
Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна.
Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –Fтр l , где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю!
Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: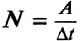 
.
Мощность показывает, какая работа совершается за 1 с.
Единица измерения мощности в СИ – ватт: [ N ] = Дж/с = Вт.
Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.
Может пригодиться! 1 л. с. (лошадиная сила) ~ 735 Вт.
Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим 
.
Для равноускоренного движения (F = const)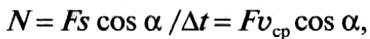 
где ʋср– средняя скорость движения за расчётный промежуток времени.
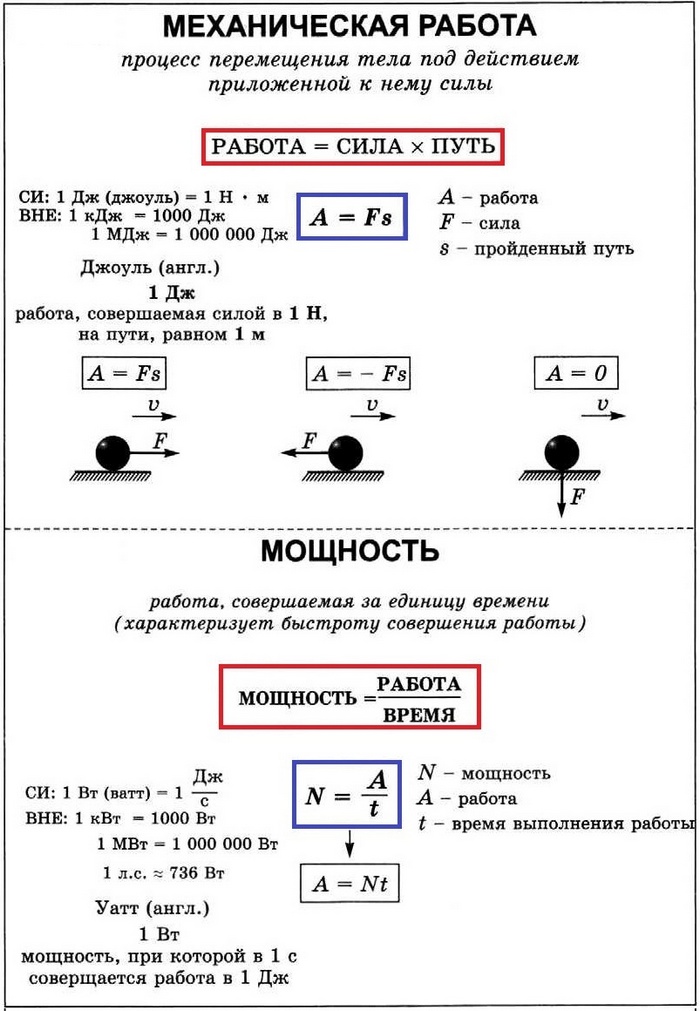
Конспект урока «Механическая работа. Механическая мощность».
Следующая тема: «Кинетическая и потенциальная энергия» (код ОГЭ 1.17)
Работа (физика) Википедия
.ts-Боковая_навигационная_таблица-preTitle{padding-top:0}.mw-parser-output .ts-Боковая_навигационная_таблица-image{padding:0.4em 0 0.4em}.mw-parser-output .ts-Боковая_навигационная_таблица-title{padding:0.2em 0.4em 0.2em;font-size:125%;line-height:1.15em;font-weight:bold;background:#cfe3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-above,.mw-parser-output .ts-Боковая_навигационная_таблица-below{padding:0.2em 0.4em 0.2em;font-weight:bold}.mw-parser-output .ts-Боковая_навигационная_таблица-heading{padding:0.2em 0;font-weight:bold;background:#eaf3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-list{padding:0.2em 0}]]>| Механическая работа |
| A
= F ⋅ S =
F
⋅
S
⋅
cos
φ {\displaystyle A={\mathbf {F}}\cdot {\mathbf {S}}=F\cdot S\cdot \cos \varphi } Работа силы |
| Ключевые статьи |
Работа в физике |
| См. также: Портал:Физика |
Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)[1].
Используемые обозначения[ |
Работа (физика) Википедия
| Механическая работа |
| A
=
F
⋅
S
=
F
⋅
S
⋅
cos
φ
{\displaystyle A={\mathbf {F}}\cdot {\mathbf {S}}=F\cdot S\cdot \cos \varphi } Работа силы |
| Ключевые статьи |
Работа в физике |
| См. также: Портал:Физика |
Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)[1].
Используемые обозначения
Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).
Определение
Работа силы, приложенной к материальной точке
Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.
При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:
- A = F s s = F s c o s ( F , s ) = F → ⋅ s → {\displaystyle A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}}
Здесь точкой обозначено скалярное произведение, s → {\displaystyle {\vec {s}}} — вектор перемещения; подразумевается, что действующая сила F → {\displaystyle {\vec {F}}} постоянна в течение времени, за которое вычисляется работа.
В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки[2]:
- A = ∫ F → ⋅ d s → . {\displaystyle A=\int {\vec {F}}\cdot {\vec {ds}}.}
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений d s → , {\displaystyle {\vec {ds}},} если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[3], интеграл определяется[4] следующим образом:
- A = ∫ r → 0 r → 1 F → ( r → ) ⋅ d r → {\displaystyle A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot {\vec {dr}}} ,
где r → 0 {\displaystyle {\vec {r}}_{0}} и r → 1 {\displaystyle {\vec {r}}_{1}} — радиус-векторы начального и конечного положения тела соответственно.
- Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.
Работа сил, приложенных к системе материальных точек
Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).
Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если A t o t a l {\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершённых приложенными к частице силами, то она выражается как:
- A t o t a l = Δ ( m v 2 2 ) = Δ E k , {\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}
где E k {\displaystyle E_{k}} называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как[5]:
- E k = 1 2 m v 2 . {\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая E p {\displaystyle E_{p}} , такая, что
- F → = − ∇ E p . {\displaystyle {\vec {F}}=-\nabla E_{p}.}
Если все силы, действующие на частицу, консервативны, и E p {\displaystyle E_{p}} является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:
- F → ⋅ Δ s → = − ∇ → E p ⋅ Δ s → = − Δ E p ⇒ − Δ E p = Δ E k ⇒ Δ ( E k + E p ) = 0 {\displaystyle {\vec {F}}\cdot \Delta {\vec {s}}=-{\vec {\nabla }}E_{p}\cdot \Delta {\vec {s}}=-\Delta E_{p}\Rightarrow -\Delta E_{p}=\Delta E_{k}\Rightarrow \Delta (E_{k}+E_{p})=0} .
Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,
- ∑ E = E k + E p {\displaystyle \sum E=E_{k}+E_{p}} ,
является постоянной во времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике
В термодинамике работа, совершённая газом при расширении[6], рассчитывается как интеграл давления по объёму:
A 1 → 2 = ∫ V 1 V 2 P d V . {\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}
Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
- d A = P d S h . {\displaystyle dA=PdSh.}
Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка M {\displaystyle M} движется по непрерывно дифференцируемой кривой G = { r = r ( s ) } {\displaystyle G=\{r=r(s)\}} , где s — переменная длина дуги, 0 ≤ s ≤ S {\displaystyle 0\leq s\leq S} , и на неё действует сила F ( s ) {\displaystyle F(s)} , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F ( s ) {\displaystyle F(s)} проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина F ( ξ i ) △ s i , △ s i = s i − s i − 1 , i = 1 , 2 , . . . , i τ {\displaystyle F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,…,i_{\tau }} , называется элементарной работой силы F {\displaystyle F} на участке G i {\displaystyle G_{i}} и принимается за приближённое значение работы, которую производит сила F {\displaystyle F} , воздействующая на материальную точку, когда последняя проходит кривую G i {\displaystyle G_{i}} . Сумма всех элементарных работ ∑ i = 1 i τ F ( ξ i ) △ s i {\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} является интегральной суммой Римана функции F ( s ) {\displaystyle F(s)} .
В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма ∑ i = 1 i τ F ( ξ i ) △ s i {\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} всех элементарных работ, когда мелкость | τ | {\displaystyle |\tau |} разбиения τ {\displaystyle \tau } стремится к нулю, называется работой силы F {\displaystyle F} вдоль кривой G {\displaystyle G} .
Таким образом, если обозначить эту работу буквой W {\displaystyle W} , то, в силу данного определения,
- W = lim | τ | → 0 ∑ i = 1 i τ F ( ξ i ) △ s i {\displaystyle W=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} ,
следовательно,
- W = ∫ 0 s F ( s ) d s {\displaystyle W=\int \limits _{0}^{s}F(s)ds} (1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра t {\displaystyle t} (например, времени) и если величина пройденного пути s = s ( t ) {\displaystyle s=s(t)} , a ≤ t ≤ b {\displaystyle a\leq t\leq b} является непрерывно дифференцируемой функцией, то из формулы (1) получим
- W = ∫ a b F [ s ( t ) ] s ′ ( t ) d t . {\displaystyle W=\int \limits _{a}^{b}F[s(t)]s'(t)dt.}
Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10−7 Дж
См. также
Примечания
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения d s → {\displaystyle {\vec {ds}}} , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введённым выше. Затем работы на всех этих перемещениях d s → {\displaystyle {\vec {ds}}} суммируется, что и даёт в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь F → ( t ) = F → ( r → ( t ) ) {\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))} ; вектор же малого перемещения d s → {\displaystyle {\vec {ds}}} совпадает с d r → {\displaystyle d{\vec {r}}} .
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫ P d V {\displaystyle \int PdV} давление подразумевается одинаковым по всему объёму (что часто выполняется в термодинамике, поскольку речь там часто идёт о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведёт к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература
- История механики с древнейших времён до конца XVIII в. В 2 т. М.: Наука, 1972.
- Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
- Льоцци М. История физики. М.: Мир, 1970.
- Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
- Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
- Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.
Механическая работа и мощность
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если действующая на тело сила вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).
Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.
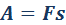
Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы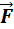 
и перемещения 
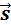(рис. 1.18.1):
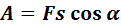
Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
|
Рисунок 1.18.1. Работа силы |
Если проекция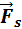 
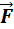силы на направление перемещения 
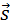не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:
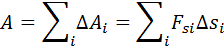
Это сумма в пределе (Δsi → 0) переходит в интеграл.
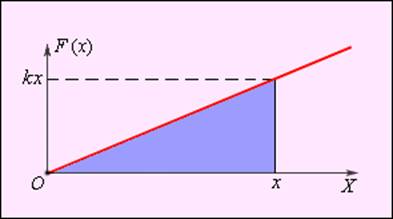
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.18.2).
|
Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi |
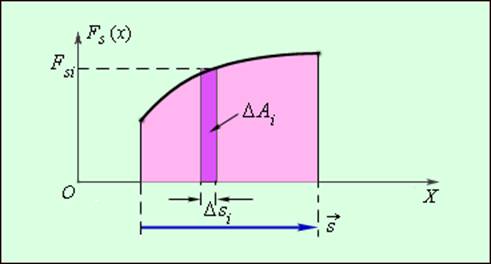
Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу 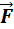модуль которой пропорционален удлинению пружины (рис. 1.18.3).
|
Рисунок 1.18.3. Растянутая пружина. Направление внешней силы
k – жесткость пружины. |
:
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).
|
Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины |
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
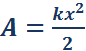
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы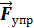 
равна по модулю работе внешней силы 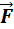и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.
 |
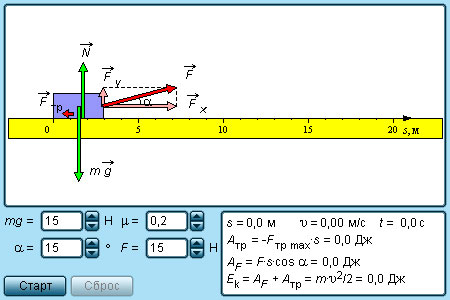Модель. Механическая работа. |
Мощность
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
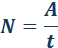
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
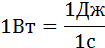
Механическая работа: определение и формула
Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?
Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа – это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом. Как так? Сейчас разберемся.
Механическая работа в физике
Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример – это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть. В каком случае совершается механическая работа?
Определение механической работы
Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.
Формула механической работы
Определяется механическая работа формулой:
A=Fs,
где A – работа,
F – сила,
s – пройденный путь.
Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.
Единица работы – 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример – это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения, то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.
Нужна помощь в учебе?
Предыдущая тема: Воздухоплавание в физике
Следующая тема:   Мощность: формула и применение в физике
Все неприличные комментарии будут удаляться.
Work (физика) — Простая английская Википедия, бесплатная энциклопедия
Бейсбольный питчер работает с мячом, передавая ему энергию.В физике сила выполняет работу , когда она воздействует на тело и точка приложения смещается в направлении силы.
Работа , совершаемая силой, действующей на тело, — это сила в направлении смещения, умноженная на смещение точки приложения.
Это сила, а не агент, создавший силу. [1] Движение — это требование работы.
Как и энергия, это скалярная величина в единицах СИ в джоулях. [2] Теплопроводность не считается формой работы, поскольку не существует макроскопически измеряемой силы, только микроскопические силы, возникающие при столкновении атомов. Термин работа был создан в 1830-х годах французским математиком Гаспаром-Гюставом Кориолисом. [3]
Согласно теореме о рабочей энергии , если внешняя сила действует на твердый объект, вызывая изменение его кинетической энергии с E k1 на E k2 , тогда механическая работа ( W ) определяется по: [4]
- W знак равно Δ Е К знак равно Е К 2 — Е К 1 знак равно м v 2 2 2 — м v 1 2 2 {\ displaystyle W = \ Delta E_ {k} = E_ {k_ {2}} — E_ {k_ {1}} = {\ frac {mv_ {2} ^ {2}} {2}} — {\ frac { mv_ {1} ^ {2}} {2}}}
, где м — масса объекта, а v — скорость объекта.
Если на объект действует постоянная сила F , в то время как объект смещен на расстояние d , а сила и смещение параллельны друг другу, работа, выполненная с объектом, является произведением F и d : [5]
- W знак равно F ⋅ d {\ Displaystyle W = F \ cdot d}
Если сила и перемещение в одном направлении, работа положительная.Если сила и смещение противоположны, работа отрицательна. Например, работа, выполняемая грузом над поднимаемой книгой, отрицательна. Это связано с тем, что вес, направленный вниз, противоположен смещению вверх.
- ↑ «Определение работы по физике». Университет Западного Вашингтона. Проверено 13 июня 2016.
- ↑ Хольцнер, Стивен (2010). Основы физики для чайников . Wiley Publishing. п. 78. ISBN 978-0-470-61841-7 .
- ↑ Джаммер, Макс (1957). Концепции силы . Dover Publications, Inc. ISBN 0-486-40689-X .
- ↑ Типлер (1991), стр.138.
- ↑ Резник, Роберт и Холлидей, Дэвид (1966), Physics , Раздел 7-2 (Том I и II, объединенное издание), Wiley International Edition, карточка каталога Библиотеки Конгресса № 66-11527
Определение работы, формула работы, факторы, влияющие на работу
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел. для класса 12
- Классы
- CBSE — вопросник за предыдущий год
- CBSE — вопросник за предыдущий год, класс 10
- CBSE — за предыдущий год — вопросник, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Физика класса 12
- Решения NCERT для химии класса 12
- Решения NCERT для биологии класса 12
- Решения NCERT для математики класса 12
- NCERT S
физика | Определение, отрасли и значение
Традиционно организованные отрасли или области классической и современной физики очерчены ниже.
Под механикой обычно понимается изучение движения объектов (или их отсутствия движения) под действием заданных сил. Классическую механику иногда считают разделом прикладной математики. Он состоит из кинематики, описания движения и динамики, изучения действия сил, вызывающих движение или статическое равновесие (последнее составляет науку о статике).Предметы квантовой механики 20-го века, имеющие решающее значение для изучения структуры вещества, субатомных частиц, сверхтекучести, сверхпроводимости, нейтронных звезд и других основных явлений, а также релятивистской механики, важной, когда скорости приближаются к скорости света, являются формами механики, будет обсуждаться позже в этом разделе.
иллюстрация закона упругости материалов Роберта Гука Иллюстрация закона упругости материалов Гука, показывающая растяжение пружины пропорционально приложенной силе, из книги Роберта Гука Lectures de Potentia Restitutiva (1678). Photos.com/JupiterimagesВ классической механике законы изначально сформулированы для точечных частиц, в которых игнорируются размеры, форма и другие внутренние свойства тел. Таким образом, в первом приближении даже такие большие объекты, как Земля и Солнце, рассматриваются как точечные, например, при расчете орбитального движения планет. В динамике твердого тела также рассматриваются удлинение тел и их массовое распределение, но предполагается, что они неспособны к деформации.Механика деформируемого твердого тела — это упругость; гидростатика и гидродинамика рассматривают жидкости в покое и в движении соответственно.
Три закона движения, сформулированные Исааком Ньютоном, составляют основу классической механики, вместе с признанием того, что силы являются направленными величинами (векторами) и соответственно сочетаются. Первый закон, также называемый законом инерции, гласит, что, если на него не действует внешняя сила, покоящийся объект остается в состоянии покоя или, если он находится в движении, он продолжает двигаться по прямой с постоянной скоростью.Следовательно, равномерное движение не требует причины. Соответственно, механика концентрируется не на движении как таковом, а на изменении состояния движения объекта в результате действующей на него чистой силы. Второй закон Ньютона уравнивает результирующую силу, действующую на объект, со скоростью изменения его количества движения, которое является произведением массы тела и его скорости. Третий закон Ньютона, закон действия и противодействия, гласит, что при взаимодействии двух частиц силы, действующие друг на друга, равны по величине и противоположны по направлению.Взятые вместе, эти механические законы в принципе позволяют определять будущие движения набора частиц, при условии, что их состояние движения известно в какой-то момент, а также силы, которые действуют между ними и на них извне. Из этого детерминированного характера законов классической механики в прошлом делались глубокие (и, вероятно, неверные) философские выводы, которые даже применимы к истории человечества.
Законы механики, лежащие на самом базовом уровне физики, характеризуются определенными свойствами симметрии, примером чему служит вышеупомянутая симметрия между силами действия и противодействия.Другие симметрии, такие как инвариантность (т. Е. Неизменная форма) законов относительно отражений и вращений, выполняемых в пространстве, обращения времени или преобразования в другую часть пространства или в другую эпоху времени, присутствуют как в классической в механике и в релятивистской механике, а также с некоторыми ограничениями в квантовой механике. Можно показать, что свойства симметрии теории имеют в качестве математических следствий основные принципы, известные как законы сохранения, которые утверждают постоянство во времени значений определенных физических величин при заданных условиях.Сохраняющиеся величины — самые важные в физике; в их число входят масса и энергия (в теории относительности масса и энергия эквивалентны и сохраняются вместе), импульс, угловой момент и электрический заряд.
.Физика: определение и направления | Owlcation
Что такое физика?
Слово «физика» происходит от латинского слова Physica , что означает «естественная вещь».
Согласно Оксфордскому словарю английского языка, физика определяется как:
Определение слова «Физика» в Оксфордском словаре английского языка
«Раздел науки, изучающий природу и свойства материи и энергии. Предметом физики являются механика, тепло, свет и другие излучения, звук, электричество, магнетизм и структура атомов.«
Другое определение из цифровой энциклопедии Microsoft Encarta описывает физику как:
Определение «физики» от Microsoft Encarta
«Крупная наука, имеющая дело с фундаментальными составляющими Вселенной, силами, которые они оказывают друг на друга, и результатами, производимыми этими силами. Иногда в современной физике используется более сложный подход, включающий элементы трех перечисленных выше областей; он относится к законам симметрии и сохранения, таким как те, которые относятся к энергии, импульсу, заряду и четности.”
Эти определения указывают на то, что физика — это отрасль науки, которая занимается свойствами материи и энергии и отношениями между ними. Он также пытается объяснить материальный мир и природные явления Вселенной.
Сфера применения физики очень широка и обширна. Он касается не только мельчайших частиц атомов, но и природных явлений, таких как галактика, Млечный путь, солнечные и лунные затмения и многое другое. Хотя это правда, что физика — это отрасль науки, в области физики есть много подразделов.В этой статье мы подробно рассмотрим каждый из них.
Какие разделы физики?
Несмотря на то, что по мере развития науки и технологий возникает больше областей, в физике обычно 11 разделов. Это следующие.
Разделы физики
- Классическая физика
- Современная физика
- Ядерная физика
- Атомная физика
- Геофизика
- Биофизика
- Механика
- Акустика
- Оптика
- Термодинамика
- Астрофизика
Продолжайте читать, чтобы подробно изучить каждую из этих ветвей.
1. Классическая физика
Этот раздел физики в основном занимается законами движения и гравитации, изложенными в кинетической теории и термодинамике сэра Исаака Ньютона и Джеймса Кларка Максвелла соответственно. Этот раздел физики в основном занимается материей и энергией. Часто физика, созданная до 1900 года, считается классической физикой, тогда как физика, созданная после 1900 года, считается современной физикой.
В классической физике энергия и материя считаются отдельными сущностями.Акустика, оптика, классическая механика и электромагнетизм традиционно являются разделами классической физики. Более того, любая физическая теория, которая считается недействительной в современной физике, автоматически попадает в сферу классической физики.
Поскольку законы Ньютона — одна из основных особенностей классической физики, давайте рассмотрим их.
Каковы три закона физики?
Три закона физики, как их обычно называют, формально известны как законы движения Ньютона.Они считаются основой классической механики. Законы Ньютона описывают движение тела, на которое могут действовать силы и которое может оказывать силы на другие тела.
Когда мы говорим о телах, мы говорим не о реальных человеческих телах (хотя человеческие тела могут быть включены в это определение), но о любой части материи, на которую может действовать сила. Ниже представлены три закона Ньютона.
Законы движения Ньютона (Три закона физики)
- Закон инерции: Тело остается в покое или равномерно движется по прямой линии, если на него не действует сила.
- Сила = Масса x Ускорение: Скорость изменения количества движения тела пропорциональна вызывающей его силе.
- Действие = Реакция: Когда сила действует на тело из-за другого тела, тогда равная и противоположная сила действует одновременно на это тело.
2. Современная физика
Современная физика — это раздел физики, который в основном связан с теорией относительности и квантовой механикой.
Альберт Эйнштейн и Макс Планк были пионерами современной физики и первыми учеными, которые представили теорию относительности и квантовую механику соответственно.
В современной физике энергия и материя не рассматриваются как отдельные сущности. Скорее, они считаются разными формами друг друга.
Каковы два столпа современной физики?
Два столпа современной физики заключаются в следующем.
- Теория относительности Альберта Эйнштейна
- Квантовая теория Макса Планка.
Что такое теория относительности?
Теория относительности Альберта Эйнштейна — одно из самых важных открытий современности. В ней утверждается, что законы физики одинаковы для всех неускоряющих наблюдателей.2
В этом уравнении «E» представляет энергию, «m» представляет массу, а «c» представляет скорость света.
Что такое квантовая теория?
Квантовая теория, открытая Максом Планком в 1900 году, является теоретической основой современной физики, объясняющей природу и поведение материи и энергии на атомном и субатомном уровнях. Природу и поведение материи и энергии на этом уровне иногда называют квантовой физикой и квантовой механикой.
Планк обнаружил, что энергия существует в отдельных единицах точно так же, как материя, а не как постоянная электромагнитная волна.Таким образом, можно было измерить энергию. Существование этих единиц, называемых квантами , лежит в основе квантовой теории Планка.
3. Ядерная физика
Ядерная физика — это раздел физики, который изучает составные части, структуру, поведение и взаимодействия атомных ядер. Эту отрасль физики не следует путать с атомной физикой, изучающей атом в целом, включая его электроны.
Согласно энциклопедии Microsoft Encarta, ядерная физика определяется как:
«Раздел физики, в котором изучаются структура, силы и поведение атомного ядра.”
В современную эпоху ядерная физика стала очень широкой по своему охвату и находит применение во многих областях. Он используется в производстве электроэнергии, ядерном оружии, медицине, магнитном резонансе, визуализации, промышленных и сельскохозяйственных изотопах и многом другом.
Кто открыл ядерную физику?
История ядерной физики как отдельной области от атомной физики начинается с открытия радиоактивности Анри Беккерелем в 1896 году. Открытие электрона годом позже показало, что атом имеет внутреннюю структуру.
Так начались исследования ядер атомов, так родилась ядерная физика.
4. Атомная физика
Атомная физика — это раздел физики, который изучает состав атома, помимо ядра. В основном это касается расположения и поведения электронов в оболочках вокруг ядра. Таким образом, атомная физика в основном изучает электроны, ионы и нейтральные атомы.
Одним из первых шагов к атомной физике было признание того, что вся материя состоит из атомов.Истинное начало атомной физики ознаменовано открытием спектральных линий и попыткой их объяснения. Это привело к совершенно новому пониманию структуры атомов и того, как они себя ведут.
5. Геофизика
Геофизика — это раздел физики, который занимается изучением Земли. В основном это связано с формой, структурой и составом Земли, но геофизики также изучают гравитационную силу, магнитные поля, землетрясения, магму и многое другое.
Геофизика была признана отдельной дисциплиной только в 19 веке, но ее истоки восходят к древним временам.Первые магнитные компасы были сделаны из
г.Все эти открытия могут быть включены в область геофизики, которая определяется как:
«естествознание, связанное с физическими процессами и физическими свойствами Земли и окружающей ее космической среды, а также использование количественных методов для их анализа».
6. Биофизика
Согласно энциклопедии Microsoft Encarta, биофизика определяется как:
«Междисциплинарное изучение биологических явлений и проблем с использованием принципов и методов физики.”
Биофизика изучает биологические проблемы и структуру молекул в живых организмах, используя методы, заимствованные из физики. Одним из самых революционных достижений биофизики является открытие Джеймсом Уотсоном и Фрэнсисом Криком структуры ДНК (дезоксирибонуклеиновой кислоты).
7. Механическая физика
Механическая физика — это раздел физики, который занимается движением материальных объектов под действием сил.
Механическая физика, которую часто называют просто механикой, подразделяется на два основных направления:
- Классическая механика
- Квантовая механика
Классическая механика занимается законами движения физических объектов и силами, вызывающими это движение, а квантовая механика — это раздел физики, который занимается поведением мельчайших частиц (т.е. электроны, нейтроны и протоны).
Каковы основные направления механики?
Механика можно разбить на восемь подразделов. Это следующие:
- Прикладная механика
- Небесная механика
- Механика сплошной среды
- Динамика
- Кинематика
- Кинетика
- Статика
- Статистическая механика
8. Акустика
Слово «акустика» происходит от греческого слова akouen , что означает «слышать.«
Следовательно, мы можем определить акустику как раздел физики, изучающий, как звук производится, передается, принимается и контролируется. Акустика также занимается звуковыми эффектами в различных средах (например, газе, жидкости и твердых телах).
9. Оптика
Оптика — это раздел физики, изучающий электромагнитное излучение (например, световое и инфракрасное излучение), его взаимодействия с веществом и инструменты, используемые для сбора информации в результате этих взаимодействий. Оптика включает изучение зрения.
Энциклопедия Microsoft Encarta определяет оптику как:
«раздел физической науки, изучающий распространение и поведение света. В общем смысле свет — это та часть электромагнитного спектра, которая простирается от рентгеновских лучей до микроволн и включает лучистую энергию, которая вызывает ощущение зрения ».
Кто изобрел оптику?
Оптика началась с создания линз древними египтянами и месопотамцами. За этим последовали теории света и зрения, разработанные древнегреческими философами, а также развитие геометрической оптики в греко-римском мире.
Эти ранние исследования в области оптики известны как классическая оптика. Исследования, появившиеся после 20-го века, такие как волновая оптика и квантовая оптика, известны как современная оптика.
10. Термодинамика
Термодинамика — это раздел физики, который изучает тепло и температуру и их связь с энергией и работой. Поведение этих величин регулируется четырьмя законами термодинамики.
Кто открыл термодинамику?
Область термодинамики была разработана на основе работ Николя Леонара Сади Карно, который считал, что эффективность двигателя является ключом, который может помочь Франции выиграть наполеоновские войны.
Шотландский физик лорд Кельвин был первым, кто дал краткое определение термодинамики. Его определение гласило:
«Термодинамика является предметом отношения тепла к силам, действующим между смежными частями тел, а также отношения тепла к электрическому действию».
Каковы четыре закона термодинамики?
Четыре закона термодинамики заключаются в следующем.
- Если две системы находятся в тепловом равновесии с третьей системой, они находятся в тепловом равновесии друг с другом.Этот закон помогает определить понятие температуры.
- Когда энергия проходит в виде работы, тепла или материи в систему или из нее, внутренняя энергия системы изменяется в соответствии с законом сохранения энергии. Точно так же невозможны вечные двигатели первого типа (машины, которые производят работу без затрат энергии).
- В естественном термодинамическом процессе сумма энтропий взаимодействующих термодинамических систем увеличивается. Точно так же вечные двигатели второго типа (машины, которые самопроизвольно преобразуют тепловую энергию в механическую работу) невозможны.
- Энтропия системы приближается к постоянному значению, когда температура приближается к абсолютному нулю. За исключением некристаллических твердых тел (стекол), энтропия системы при абсолютном нуле обычно близка к нулю и равна натуральному логарифму произведения основных квантовых состояний.
11. Астрофизика
Слово «астрофизика» — это комбинация двух слов, образованных от латинского: astro , что означает «звезда», и phisis , что означает «природа ». «
Таким образом, астрофизику можно определить как раздел астрономии, который занимается изучением Вселенной (то есть звезд, галактик и планет) с использованием законов физики.
В чем разница между астрофизиком и астрономом?
С технической точки зрения астрономы измеряют только положение и характеристики небесных тел, тогда как астрофизики используют прикладную физику для понимания астрономии.
Однако теперь эти термины используются как синонимы, поскольку все астрономы используют физику для проведения своих исследований.
,
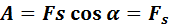