Число оборотов в единицу времени есть величина, обратная периоду. Она называется частотой вращения

.(3)

Нетрудно получить связь между угловой и линейной скоростью точки.

При движении по окружности элемент дуги связан с бесконечно малым поворотом соотношением . Отсюда .

Подставив его в (1), находим, что модуль линейной скорости будет равен

. (4)

Формула (4) связывает величины угловой и линейной скоростей.

Более общее соотношение очевидно из чертежа, где вектор линейной скорости представляет собой векторное произведение вектора угловой скорости – и радиуса-вектора точки :

. (5)

Справочный материал.

1. Векторным произведениемвекторовиназывается вектор, величина которого равна площади параллелограмма, построенного на векторах сомножителях, а собственно векторы ,иобразуют правую тройку векторов.

2. Векторы { ,,} образуют правую тройку, если кратчайший поворот от вектора к вектору , видимый из конечной точки вектора , может быть произведен в направлении «против часовой стрелки».

Определение 5.

Угловое ускорение — это производная по времени от вектора угловой скорости (соответственно вторая производная по времени от угла поворота)

3. Примеры расчёта кинематических характеристик автомобиля.

Пример №1.

Гоночный автомобиль движется на прямолинейном участке траектории так, что его ускорение растёт линейно и за первые 10с достигает значения 5 м/с². Пренебрегая его собственными размерами и массой, определить в конце 10-ой секунды: 1) скорость автомобиля; 2) пройденный им путь.

Решение.

Поскольку ускорение растёт линейно, то и неизвестный коэффициент пропорциональности – м/с.

По условию движение – прямолинейно, следовательно, скорость –

м/с. (1)

Пройденный путь прямолинейного движения будет равен:

м. (2)

Ответы:

1) по формуле (1) – м/с; 2) по формуле (2) – м.

Пример №2.

Трековая модель автомобиля вращается на привязи с частотой Гц. После прекращения тяги, модель, сделав оборотов, остановилась. Пренебрегая собственными размерами и массой модели автомобиля, определить её угловое ускорение – , если считать, что торможение является равнозамедленным.

Решение.

Поскольку торможение принимается равнозамедленным, то угол поворота –

(1),

где угловая частота вращения, Гц (2).

Конечное значение угла – рад (3).

Конечное значение угловой частоты вращения – , следовательно из соотношения – , где момент остановкис (4).

Подставляя в выражение (1) соотношения (2), (3), (4), находим, что рад/c.

Примечание.Решение можно получить в общем виде, полагая, что определены общими выражениями – (2÷4). Тогда рад/c.

Смотря по тому, остается ли число оборотов в единицу времени постоянным, увеличивается ли оно или уменьшается, различают:

Зная число оборотов в единицу времени, можно вычислить окружную скорость.

Когда вращающийся диск совершает один оборот, то каждая точка диска описывает окружность. Вычислим окружную скорость точки, т. е. длину пути, который она проходит за единицу времени (в технике за 1 минуту). Очевидно, для этого надо умножить длину окружности на число оборотов в единицу времени.

Окружная скорость = Длина окружности X Число оборотов в единицу времени.

Обозначая окружную скорость через v, длину окружности через С и число оборотов за единицу времени через п, получим:

Смотря по тому, остается ли число оборотов в единицу времени постоянным, увеличивается ли оно или уменьшается, различают:

1) равномерное вращательное движение,

2) ускоренное вращательное движение,

3) замедленное вращательное движение.

Когда говорят о колеблющемся теле, то число колебаний в секунду называют частотой /, а время, в течение которого совершается одно полное колебание,- периодом Т. В этом случае, как и при вращательном движении, справедлива формула f-T — l (стр. 62).

При работе на сверлильном, токарном, фрезерном станках скорость резания (скорость перемещения инструмента относительно обрабатываемой детали) выбирают в зависимости от материала обрабатываемой детали, от применяемого режущего инструмента, от требуемой точности обработки и типа станка. Число оборотов станка, соответствующее условиям работы, определяют по так называемой лучевой диаграмме скорости резания (рис. 62).

Упражнения:

76. Пропеллер пассажирского самолета совершает 1500 оборотов в минуту. Вычислить число оборотов в секунду. Вычислить период и окружную скорость, если пропеллер описывает окружность диаметром 3 м.

77. Ротор электродвигателя совершает 1400 оборотов в минуту, Каков период вращения в минутах? В секундах?

 

 

 

Обороты, единицы измерения — Справочник химика 21

    Если угол измеряют в градусах, то осуществляют перевод единиц измерения с помощью следующего соотношения.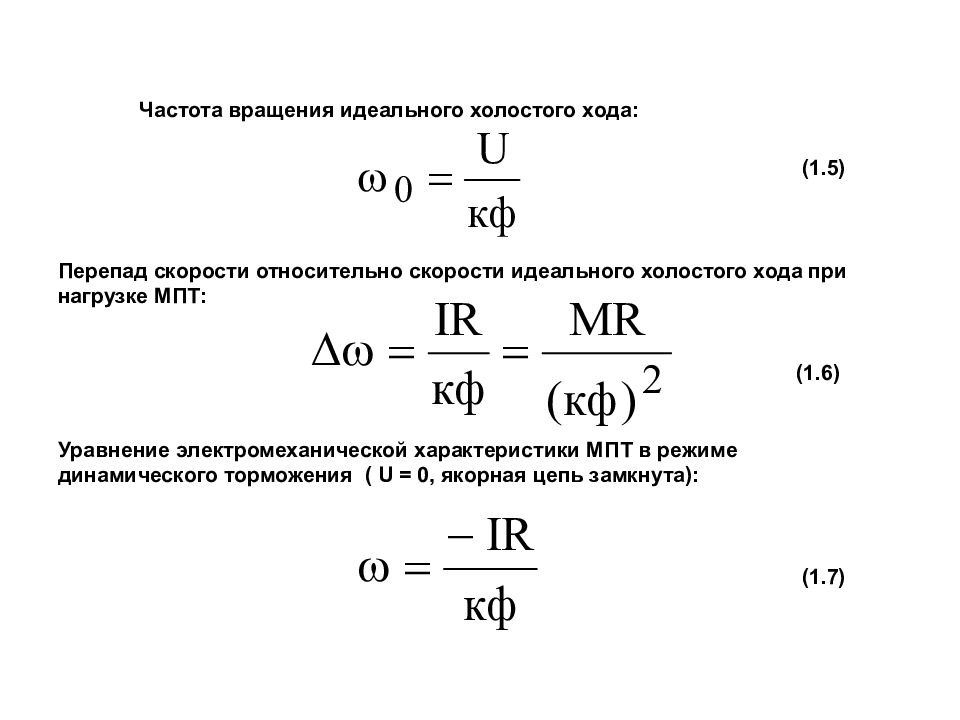

При повороте тела на один оборот его угловое перемещение составляет 360° и в радианах 2п рад, поэтому величина радиана в градусном измерении равна  [c.138]

    В технике часто быстроту вращения твердого тела характеризуют частотой вращения, которая показывает, сколько оборотов вокруг оси совершает вращающееся тело в единицу времени. Единицами измерения частоты вращения являются 1 об/мин (оборот в минуту) или 1 об/с (оборот в секунду). Частоту вращения обозначают латинской буквой п. [c.139]

    Для измерения числа оборотов червяка и скоростей работы отдельных механизмов, т. е. скорости движения изделия, используются вольтметры, подключенные к тахогенераторам, соединенным с двигателями механизмов. Шкалы вольтметров градуированы соответственно в единицах чисел оборотов и в единицах скорости движения изделия. [c.341]

    Угол оплетения получается в результате движения двух видов. За единицу измерения движения принимают расстояние, пройденное за единицу времени. Практически имеется в виду продолжительность 1 оборота шпуледержателя вокруг оси (см. гл. 7). 

[c.59]

    Существуют две единицы измерения скорости зубчатых передач. Первая и наиболее распространенная единица измерения — число оборотов в единицу времени об мин). Но эта единица измерения не является определяющей, а выражает частоту контакта зубьев. Вторая и более определенная единица измерения скорости шестерен — линейная скорость, измеряемая в л /с /с (скорость скольжения по линии зацепления) . [c.20]

    Рассматриваемый способ применяется для потоков с большими поперечными сечениями в трубопроводах, в открытых руслах. В трубопроводах скорость обычно измеряют гидродинамическими трубками, в открытых руслах — специальными приборами, так называемыми гидродинамическими вертушками, которые устроены аналогично скоростному турбинному счетчику и измеряют местную скорость потока по числу оборотов колеса в единицу времени.

Точность измерения расхода зависит от точности измерения скоростей и площадей участков, а также от числа участков (которое должно выбираться достаточно большим). [c.91]

    Стоимостной измеритель для каждой части конечной продукции должен быть выбран с таким расчетом, чтобы, во-первых, обеспечить возможность их суммирования и исчисления единого, обобщающего показателя во-вто-рых, обеспечить отражение реального трудового вклада коллектива производственной единицы в изготовление конечной продукции. Это возможно достигнуть следующим образом. Для исчисления обобщающего показателя объема товарной (отгруженной, реализуемой) продукции производственной единицы необходимо внутренний оборот измерять в оптовых ценах предприятия, а в случае их отсутствия во внутренних ценах, исчисленных по аналогии с оптовыми ценами предприятия. В этом случае структура показателя объема товарной (отгруженной, реализуемой) продукции будет представлять собой сумму двух единообразно измеренных слагаемых  

[c.

270]

    Н-м (150 гс-см), по шкале Б — 3,0-10″ Н-м (300 гс-см). При определении вращающего момента по шкале Б применяется добавочный груз 19, надеваемый на стержень измерителя вращающего момента. Для охлаждения подшипников электродвигателя кронштейн 15 снабжен водяной рубашкой. Вода поступает через штуцер 20 и отводится по шлангу. Нагрев камеры осуществляется электронагревателями 2, помещенными на дно камеры. Регулирование и поддержание температуры на заданном уровне осуществляется контактным термометром 13. Число оборотов электродвигателя определяется с помощью тахо-генератора 17 и милливольтметра 25. Тахогенератор крепится к кронштейну 15, а его вал соединен с валом электродвигателя. При вращении электродвигателя в тахогенераторе возбуждается э. д. с., пропорциональная скорости вращения. Измерение э. д. с. производится милливольтметром 25. Плавное регулирование скорости вращения двигателя осуществляется вручную с помощью автотрансформатора типа ЛАТР-2. На пульте управления 24 имеется график перевода показаний милливольтметра в единицы частоты вращения двигателя. [c.158]

    Пластичность жидкости можно показать с помощью вискозиметра Штормера, действие которого заключается во вращении цилиндрика или лопастной мешалки в сосуде с исследуемой жидкостью. Мешалка приводится в движение с помощью нити, навернутой на ее ось, и с помощью блоков, к которым подвешена чашка с грузиками. Нагрузка чашки соответствует натяжению в жидкости, а измеряемое количество оборотов в единицу времени — градиенту ёи/йу. Результаты измерений ]1ри различных оборотах составляют линию, похожую на представленную на рис. 2-21. После соответствующей калибровки из полученного 1 рафика на основании этих измерений можно найти вязкость для вязких жидкостей, а также пластичность 1 и минимальное напряжение То для пластичных жидкостей. [c.117]

    Точное регулирование горения в печах с пылеугольным отол-лением легче, чем в печах, в которых сжигается кусковое топливо на решетках. Это объясняется тем, что при постоянных тонкости помола, влажности и аэрации пыли расход последней может быть достаточно точно измерен. Вес пыли, расходуемой в единицу времени, пропорционален числу оборотов питателя вес воздуха, подведенного к печи за то же время, пропорционален корню квадратному от величины лерепада давления на измерительной диафрагме. [c.222]

    Для испытания по методу А образец помещают на стол, прикладывают предварительную нагрузку и устанавливают стрелку индикатора. По истечении 10 с после приложения предварительной нагрузки прикладывают основную нагрузку, которую снимают через 15 с после приложения. Через 15 с после снятия нагрузки записывают показания индикатора с точностью до целого деления (шкала твердомера, используемая в методе А, обозначается красным цветом). Расстояние между краем образца и центром отпечатка должно быть во всех случаях не менее 6 мм. Испытание проводят только на одной стороне образца. Параллельно проводят пять измерений. Если шкала прибора градуирована в единицах твердости по Роквеллу, то показатель твердости определяют непосредственно по шкале прибора, увеличивая значение, указанное на шкале, на 100, если стрелка индикатора при приложении основной нагрузки и при снятии ее прошла одинаковое число раз через ноль сохраняя значение по шкале прибора, если при снятии основной нагрузки стрелка индикатора прошла через ноль на один оборот меньше, и уменьшая его на 100, если стрелка индикатора при снятии нагрузки прошла через ноль на два оборота меньше в этом случае значение твердости записывается как отрицательная величина, например, —5=95—100. [c.270]

    Различают два типа ротационных вискозиметров. В приборах первого типа один из цилиндров неподвижен. Иэмерение сводится к определению числа оборотов подвижного цилиндра в единицу времени или к определению времени одного оборота цилиндра. Эти вискозиметры применяются для вязких жидкостей и пластических тел. С их помощью также может быть измерено предельное напряжение сдвига. К вискозиметрам первого типа относится вискозиметр ВоЛаровича. Этот вискозиметр отличается способом устранения искажающего влияния концов цилиндра на результаты измерения (цилиндры заканчиваются полушариями), тщательным термостатированием и рядом удобных приспособлений, облегчающих измерения. [c.192]

    Анемометром производят непосредственное измерение скорости газового потока. Анемометры устроены по принципу крыльчатки-вертушки, которая струей газа приводится во вращение. По числу оборотов крыльчатки в единицу времени судят о скорости потока газа. Крыльчатка анемометра может работать как вхолостую, так и с включением счетчика, отмечающего показания стрелками на циферблате. К анемометру приложен паспорт, содержащий коэфициенты для пересчета показаний счетчика при вычислении скорости газового потока. Анемометры имеют пределы скоростей, при которых они могут употребляться. Пределы эти указаны на паспорте. Обычные анемометры чувствительны начиная со скоростей около 1 м сек. При скоростях больше 10 м сек крылья анемометра гнутся, и он работает неправильно. Для малых скоростей можно пользоваться дифе-ренциальным анемометром. [c.26]

    Интегратор прибора ЭПИД рассчитан так, что, если стрелка прибора находится на максимальной отметке шкалы, число оборотов якоря муфты и, следовательно, изменение показаний счетчика составляет 100 единиц в 1 ч. Таким образом, постоянная интегратора приборов ЭПИД равна /Син = 0,01 Qmax (Qmax — верхний предел измерения по расходу. Шкалы приборов ЭПИД, предназначенных для измерения расхода, линейны по расходу. Выпрямление шкалы достигают путем применения лекал 4 (см. рис. 188) с квадратичным профилем. [c.460]

    ЕДИНЙЦЫ МОЩНОСТИ ПРОИЗВОДСТВЕННОГО ОБОРУДОВАНИЯ — величины, принятые за основу измерения работы станков, машин, агрегатов и другого оборудования в единицу времени (секунду, час, смену, сутки и т. д.). В связи с разнообразием производственного оборудования и вырабатываемой с его помощью продукции в статистике применяется несколько видов Е. м. п. о. Конструктивная форма Е. м. п. о. определяется в основном способом измерения результатов работы производственного оборудования. На практике чаще всего применяются натуральные или условные натуральные единицы продукции. Е. м. п. о. в данном случае будут представлены сочетанием единицы меры веса, объема и т. д. и единицы времени, напр, для врубовой машины-—т добываемого угля в час, земснаряда— намываемого грунта в час и т. д. Если работа оборудования характеризуется количеством движений рабочего органа, то в качестве Е. м. п. о. может служить определенного вида движение рабочего органа в единицу времени, напр, удар батана в секунду для ткацкого станка или оборот веретена в секунду для прядильного оборудования и т. д. В ряде случаев мощность производственного оборудования измеряется физич. единицами мощности (киловаттами, лошадиными силами и т. д.), напр, для токарного станка — киловаттами мощности его иа резце. Кроме того, в экономич. статистике мощность производственного оборудования выражается количеством или размером рабочих органов машины или агрегата для этого используются обычные физич. единицы меры, веса, объема, площади и т. д., нанр. для доменной печи — м по.пезного объема, для подъемного крана — т груза, для экскаватора —. и емкости ковша и т. д. [c.222]

    Вискозиметр (рис. 5-17) представляет собой сосуд с исследуемой жидкостью, в котором находится лопастная мешалка. Движение мешалки осуществляется при помощи троса, блока и чашки с грузом. Измерение вязкости основано на измерении зависимости между грузо.м чашки G и числом оборотов мешалки в единицу времени п. Для обычных жидкостей эту зависимость можно представить в виде прямой линии (рис. 5-18, /). Так как нагрузка чашки находится в некотором отношении к внутренним напряжениям в жидкости т, а число оборотов — к градиенту скорости dujdx, то согласно уравнению вязкости [c.298]

---

Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Таким образом,

 Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

   

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: . Итак,

   

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

   

Частоту в СИ измеряют в

   

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

1. Приведите два-три примера криволинейного движения.
2. Приведите два-три примера равномерного движения по кругу.
3. Что такое вращательное движение? Приведите примеры такого движения.
4. Как направлена ​​мгновенная скорость при движении по кругу Приведите два-три примера.

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением:  Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Мощность и крутящий момент — что это?

ЧТО ТАКОЕ ЛОШАДИНАЯ СИЛА?

— У тебя сколько сил? — такой вопрос слышал любой, кто хоть немного касался мира автомобилей. Никому даже пояснять не надо, какие силы на самом деле имеются в виду — лошадиные. Именно в них мы привыкли оценивать мощность мотора, одну из важнейших потребительских характеристик машины.

Уже и гужевого транспорта практически не осталось даже в деревнях, а эта единица измерения живёт и здравствует больше ста лет. А ведь лошадиная сила — величина, по сути, нелегальная. Она не входит в международную систему единиц (полагаю, многие со школы помнят, что называется она СИ) и потому не имеет официального статуса. Более того, Международная организация законодательной метрологии требует как можно скорее изъять лошадиную силу из обращения, а директива ЕС 80/181/EEC от 1 января 2010 прямо обязует автопроизводителей использовать традиционные «л.с.» только как вспомогательную величину для обозначения мощности.

Но не зря считается, что привычка — вторая натура. Ведь говорим же мы в обиходе «ксерокс» вместо копир и обзываем клейкую ленту «скотчем». Вот и непризнанные «л.с.» сейчас используют не только обыватели, но и едва ли не все автомобильные компании. Какое им дело до рекомендательных директив? Раз покупателю удобнее — пусть так и будет. Да что там производители — даже государство на поводу идёт. Если кто забыл, в России транспортный налог и тариф ОСАГО именно от лошадиных сил высчитываются, как и стоимость эвакуации неправильно припаркованного транспорта в Москве.

Лошадиная сила родилась в эпоху промышленной революции, когда потребовалось оценить, насколько эффективно механизмы заменяют животную тягу. По наследству от стационарных двигателей эта условная единица измерения мощности со временем перешла и на автомобили

И никто бы к этому не придирался, если не одно весомое «но». Задуманная, чтобы упростить нам жизнь, лошадиная сила на самом деле вносит путаницу. Ведь появилась она в эпоху промышленной революции как совершенно условная величина, которая не то что к автомобильному мотору, даже к лошади имеет достаточно опосредованное отношение. Смысл этой единицы в следующем — 1 л.с. достаточно, чтобы поднять груз массой 75 кг на высоту 1 метр за 1 секунду. Фактически, это сильно усреднённый показатель производительности одной кобылы. И не более того.

Иными словами, новая единица измерения очень пригодилась промышленникам, добывавшим, к примеру, уголь из шахт, и производителям соответствующего оборудования. С её помощью было проще оценить преимущество механизмов над животной силой. А поскольку приводились станки уже паровыми, а позднее и керосиновыми двигателями, то «л.с.» перешли по наследству и к самобеглым экипажам.

Джеймс Уатт — шотландский инженер, изобретатель, учёный, живший в XVIII — начале XIX века. Именно он ввёл в обращение как «нелегальную» сейчас лошадиную силу, так и официальную единицу измерения мощности, которую назвали его именем

По иронии судьбы изобрёл лошадиную силу человек, именем которого названа официальная единица измерения мощности — Джеймс Уатт. А поскольку ватт (а точнее, применительно к могучим машинам, киловатт — кВт) к началу XIX века тоже активно входил в оборот, пришлось две величины как-то приводить друг к другу. Вот здесь-то и возникли ключевые разногласия. Например, в России и большинстве других европейских стран приняли так называемую метрическую лошадиную силу, которая равна 735,49875 Вт или, что сейчас нам более привычно, 1 кВт = 1,36 л.с. Такие «л.с.» чаще всего обозначают PS (от немецкого Pferdestärke), но есть и другие варианты — cv, hk, pk, ks, ch… При этом в Великобритании и ряде её бывших колоний решили пойти своим путём, организовав «имперскую» систему измерений с её фунтами, футами и прочими прелестями, в которой механическая (или, по-другому, индикаторная) лошадиная сила составляла уже 745,69987158227022 Вт. А дальше — пошло-поехало. К примеру, в США придумали даже электрическую (746 Вт) и котловую (9809,5 Вт) лошадиные силы.

Вот и получается, что один и тот же автомобиль с одним и тем же двигателем в разных странах на бумаге может иметь разную мощность. Возьмём, например, популярный у нас кроссовер Kia Sportage — в России или Германии по паспорту его двухлитровый турбодизель в двух вариантах развивает 136 или 184 л.с., а в Англии — 134 и 181 «лошадку». Хотя на самом деле отдача мотора в международных единицах составляет ровно 100 и 135 кВт — причём в любой точке земного шара. Но, согласитесь, звучит непривычно. Да и цифры уже не такие впечатляющие. Поэтому автопроизводители и не спешат переходить на официальную единицу измерения, объясняя это маркетингом и традициями. Это как же? У конкурентов будет 136 сил, а у нас всего 100 каких-то кВт? Нет, так не пойдёт…

КАК ИЗМЕРЯЮТ МОЩНОСТЬ?

Впрочем, «мощностные» хитрости игрой с единицами измерения не ограничиваются. До последнего времени её не только обозначали, но даже измеряли по-разному. В частности, в Америке долгое время (до начала 1970-х годов) автопроизводители практиковали стендовые испытания двигателей, раздетых догола — без навески вроде генератора, компрессора кондиционера, насоса системы охлаждения и с прямоточной трубой вместо многочисленных глушителей. Само собой, сбросивший оковы мотор легко выдавал процентов на 10-20 больше «л.с.», так необходимых менеджерам по продажам. Ведь в тонкости методики испытаний мало кто из покупателей вдавался.

Другая крайность (но гораздо более приближенная к реальности) — снятие показателей прямо с колёс автомобиля, на беговых барабанах. Так поступают гоночные команды, тюнинговые мастерские и прочие коллективы, которым важно знать отдачу мотора с учётом всех возможных потерь, и трансмиссионных в том числе.

Мощность также зависит от того, как её измерять. Одно дело крутить на стенде «голый» мотор без навесного оборудования и совсем другое — снимать показания с колёс, на беговых барабанах, с учётом трансмиссионных потерь. Современные методики предлагают компромиссный вариант — стендовые испытания двигателя с необходимой для его автономной работы навеской

Но в итоге за образец в различных методиках вроде европейских ECE, DIN или американских SAE приняли компромиссный вариант. Когда двигатель устанавливают на стенде, но со всей необходимой для бесперебойного функционирования навеской, включая стандартный выпускной тракт. Снять можно только оборудование, относящееся к другим системам машины (к примеру, компрессор пневмоподвески или насос гидроусилителя руля). То есть тестируют мотор ровно в том виде, в котором он фактически стоит под капотом автомобиля. Это позволяет исключить из финального результата «качество» трансмиссии и определить мощность на коленвале с учётом потерь на привод основных навесных агрегатов. Так, если говорить о Европе, то эту процедуру регламентирует директива 80/1269/EEC, впервые принятая ещё в 1980 году и с тех пор регулярно обновляемая.

ЧТО ТАКОЕ КРУТЯЩИЙ МОМЕНТ?

Но если мощность, как говорят в Америке, помогает автомобили продавать, то двигает их вперёд крутящий момент. Измеряют его в ньютон-метрах (Н∙м), однако у большинства водителей до сих пор нет чёткого представления об этой характеристике мотора. В лучшем случае обыватели знают одно — чем выше крутящий момент, тем лучше. Почти как с мощностью, не правда ли? Вот только чем тогда «Н∙м» отличаются от «л.с.».?

На самом деле, это связанные величины. Более того, мощность — производная от крутящего момента и оборотов мотора. И рассматривать их по отдельности просто нельзя. Знайте — чтобы получить мощность в ваттах необходимо крутящий момент в ньютон-метрах умножить на текущее число оборотов коленвала и коэффициент 0,1047. Хотите привычные лошадиные силы? Нет проблем! Делите результат на 1000 (таким образом получатся киловатты) и умножайте на коэффициент 1,36.

Чтобы обеспечить дизелю (на фото слева) высокую степень сжатия, инженеры вынуждены делать его длинноходным (это когда ход поршня превышает диаметр цилиндра). Поэтому у таких моторов крутящий момент конструктивно получается большим, но предельное число оборотов приходится ограничивать ради повышения ресурса. Разработчикам бензиновых агрегатов, наоборот, проще получить высокую мощность — детали здесь не такие массивные, степень сжатия меньше, так что двигатель можно сделать короткоходным и высокооборотным. Впрочем, в последнее время различие между дизелями и бензиновыми агрегатами постепенно стирается — они становятся всё более похожими как по конструкции, так и по характеристикам

Выражаясь техническим языком, мощность показывает, сколько работы способен выполнить мотор за единицу времени. А вот крутящий момент характеризует потенциал двигателя к совершению этой самой работы. Показывает сопротивление, которое он может преодолеть. Например, если машина упрётся колёсами в высокий бордюр и не сможет тронуться с места, мощность будет нулевой, так как никакой работы мотор не совершает — движения нет, но крутящий момент при этом развивается. Ведь за то мгновение, пока движок не заглохнет от натуги, в цилиндрах сгорает рабочая смесь, газы давят на поршни, а шатуны стараются привести во вращение коленвал. Иными словами, момент без мощности существовать может, а мощность без момента — нет. То есть именно «Н∙м» являются основной «продукцией» двигателя, которую он производит, превращая тепловую энергию в механическую.

Если проводить аналогии с человеком, «Н∙м» отражают его силу, а «л.с.» — выносливость. Именно поэтому тихоходные дизельные двигатели в силу своих конструктивных особенностей у нас, как правило, тяжелоатлеты — при прочих равных условиях они могут тащить на себе больше и легче преодолевают сопротивление на колёсах, пусть и не так проворно. А вот быстроходные бензиновые моторы скорее относятся к бегунам — нагрузку держат хуже, зато перемещаются быстрее. В общем, действует простое правило рычага — выигрываем в силе, проигрываем в расстоянии или скорости. И наоборот.

Так называемая внешняя скоростная характеристика двигателя отражает зависимость мощности и крутящего момента от оборотов коленвала при полностью открытом дросселе. По идее, чем раньше наступает пик тяги и позже — мощности, тем проще мотору адаптироваться к нагрузкам, его рабочий диапазон увеличивается, что позволяет водителю или электронике реже переключать передачи и почём зря не жечь топливо. На этих графиках видно, что бензиновый двухлитровый турбомотор (справа) выигрывает по этому показателю у турбодизеля аналогичного объёма, но уступает ему в абсолютной величине крутящего момента

Как это выражается на практике? В первую очередь, надо понять, что именно кривые крутящего момента и мощности (вместе, а не по отдельности!) на так называемой внешней скоростной характеристике двигателя будут раскрывать его истинные возможности. Чем раньше достигается пик тяги и позже пик мощности, тем лучше мотор приспособлен к своим задачам. Возьмём простой пример — автомобиль движется по ровной дороге и вдруг начинается подъём. Сопротивление на колёсах возрастает, так что при неизменной подаче топлива обороты станут падать. Но если характеристика двигателя грамотная, крутящий момент при этом наоборот начнёт расти. То есть мотор сам приспособится к увеличению нагрузки и не потребует от водителя или электроники перейти на передачу пониже. Перевал пройден, начинается спуск. Машина пошла на разгон — высокая тяга здесь уже не так важна, критичным становится другой фактор — мотор должен успевать её вырабатывать. То есть на первый план выходит мощность. Которую можно регулировать не только передаточными числами в трансмиссии, а повышением оборотов двигателя.

Здесь уместно вспомнить гоночные автомобильные или мотоциклетные моторы. В силу относительно небольших рабочих объёмов, они не могут развить рекордный крутящий момент, зато способность раскручиваться до 15 тысяч об/мин и выше позволяет им выдавать фантастическую мощность. К примеру, если условный двигатель при 4000 об/мин обеспечивает 250 Н∙м и, соответственно, примерно 143 л.с., то при 18000 об/мин он мог бы выдать уже 640,76 л.с. Впечатляет, не правда ли? Другое дело, что «гражданскими» технологиями это не всегда получается добиться.

И, кстати, в этом плане близкую к идеальной характеристику имеют электродвигатели. Они развивают максимальные «ньютон-метры» прямо со старта, а потом кривая крутящего момента плавно падает с ростом оборотов. График мощности при этом прогрессивно возрастает.

Современные моторы «Формулы 1» имеют скромный объём 1,6 л и относительно невысокий крутящий момент. Но за счёт турбонаддува, а главное — способности раскручиваться до 15000 об/мин, выдают порядка 600 л.с. Кроме того, инженеры грамотно интегрировали в силовой агрегат электродвигатель, который в определённых режимах может добавлять ещё 160 «лошадок». Так что гибридные технологии могут работать не только на экономичность

Думаю, вы уже поняли — в характеристиках автомобиля важны не только максимальные значения мощности и крутящего момента, но и их зависимость от оборотов. Вот почему журналисты так любят повторять слово «полка» — когда, допустим, мотор выдаёт пик тяги не в одной точке, а в диапазоне от 1500 до 4500 об/мин. Ведь если есть запас крутящего момента, мощности тоже, скорее всего, будет хватать.

Но всё же лучший показатель «качества» (назовём его так) отдачи автомобильного двигателя — его эластичность, то есть способность набирать обороты под нагрузкой. Она выражается, например, в разгоне от 60 до 100 км/ч на четвёртой передаче или с 80 до 120 км/ч на пятой — это стандартные тесты в автомобильной индустрии. И может случиться так, что какой-нибудь современный турбомотор с высокой тягой на малых оборотах и широченной полкой момента даёт ощущение отличной динамики в городе, но на трассе при обгоне окажется хуже древнего атмосферника с более выгодной характеристикой не только момента, но и мощности…

Так что пусть в последнее время разница между дизельными и бензиновыми агрегатами становится всё более расплывчатой, пусть развиваются альтернативные моторы, но извечный союз мощности, крутящего момента и оборотов двигателя останется актуальным. Всегда.

Измерение частоты для индикации числа оборотов и скорости T set 1

Комбинация  Tset1 предназначена для индикации числа оборотов или скорости и, как пример, применяется при:

    * тактовой индикации печатных машин
    * контроле скорости подачи в экструдерах
    * индикации числа оборотов приводов
    * контроле скорости в проходных печах

Для измерения частоты достаточно сигнала, который может быть взят от датчика расстояния, от светового затвора или непосредственно от блока управления. Расчет базируется на измерении периода сигнала, достаточно просчитать число импульсов за единицу времени. Это справедливо также для различных диаметров мерных колес или вальцов.

Пример расчета:
Энкодер выдает 500 имп/оборот (или 500 1/мин)., периметр мерного колеса составляет 0,5 м. Расчет показаний 500 / 0,5 = 1000 м/мин, именно это значение выдается на дисплей.

В комплект входят:
* TA200.002AXA1 — электронный тахометр с большим 6-значным LED-дисплеем. Счет реализован через постоянное измерение периода импульсов. Количество импульсов за единицу времени, десятичных знаков, интервалов измерения программируется.
* GI355.070C315 — инкрементальный энкодер с зажимным фланцем.
* Z141.003  — штеккер с кабелем.
* Z119.017 — крепление для энкодера.

Частота счета до 40 кГц. Опционально: PG-штеккер с кабелем. Опционально: мерное колесо 1R542.10D с периметром 50 см и поверхностным слоем Hytrel.

Точность +/- Измеряемая точность 1/ч, 1/мин, 1/с.
Предел измерений 999999
Напряжение 230 VAC или 24 VDC
Энергоснабжение датчика 12… 26 VDC
Вход Дигитальный вход. Энкодер с зажимным фланцем, 500 имп/оборот, A 90 град. B
Подключение клеммы
Высота цифр на дисплее 14 мм.

Равномерное круговое движение

Введение

Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории. Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f . Период — это время, необходимое для того, чтобы объект совершил один оборот движения.Угловая скорость — это угловое смещение в секунду, которое связано с частотой следующим образом: с ω в рад / с. Частота вращения — это количество оборотов в секунду, которое определяется по формуле: с f в Гц или сек ^-1 . Скорость объекта является касательной к окружности с величиной v = rω . Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с a м / с ² .Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила. Величина чистой силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в N. Эта центростремительная сила может быть обеспечена натяжением (как в этой лаборатории), трением (как для автомобиля, движущегося по кривой), нормальной силой (как в петлеобразных американских горках) или гравитацией (как для движения спутника).В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F . По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить его со значением массы, полученным путем непосредственного взвешивания его на весах.

Аппарат UCM

Аппарат UCM состоит из платформы с регулируемой скоростью вращения .На расстоянии r от центра вращения находится узел боковой стойки , на котором висит объект массой м , называемый вращающейся массой (не путать со статической массой ). Вращающаяся масса прикреплена к пружине на центральной стойке с помощью струны и небольшого шкива. Когда платформа вращается, вращающаяся масса будет перемещаться по круговой траектории из-за силы, прилагаемой к ней струной (посредством натяжения пружины).Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, косвенное измерение этой силы будет производиться с использованием веса статической массы, как показано и объяснено ниже.

Рисунок 1

Когда платформа не вращается, вращающаяся масса не свисает вертикально с боковой стойки, а, скорее, втягивается внутрь за счет натяжения струны и пружины. При проведении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r .Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.

Рисунок 2

Период вращения измеряется секундомером . Платформу можно вращать, поворачивая стержень с накаткой вручную.

Процедура

Выравнивание оборудования

Если платформа неровная, это отрицательно скажется на ваших результатах. Студенты первой лаборатории недели должны были уже выровнять прибор.Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы. Если ваше устройство необходимо выровнять, выполните следующие действия.

• 1

  Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства до тех пор, пока пузырь не будет отцентрирован.

• 2

  Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа неровная, тяжелый конец будет качаться в низкую сторону.

• 3

  Отрегулируйте регулировочные винты на ножках основания до тех пор, пока конец платформы не будет качаться равномерно, когда ее осторожно поворачивают вручную.

Установка радиуса

• 1

  Осторожно отсоедините вращающуюся массу от струн.Используйте весы, чтобы взвесить его, и запишите значение массы.

• 2

  Подвесьте вращающуюся гирю к боковой стойке и подсоедините шнур от пружины к гири. Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.

• 3

  Переместите кронштейн индикатора на центральной стойке в самое нижнее положение.

• 4

  Вытяните вращающуюся массу от центральной стойки, пока оранжевый индикатор не окажется в центре кронштейна.Если струна, поддерживающая вращающийся груз, не является вертикальной, когда индикатор выровнен с кронштейном, боковую стойку следует перемещать внутрь или наружу, пока струна не станет вертикальной. Используйте вертикальную линию на боковой стойке, чтобы облегчить это выравнивание. При затягивании боковой стойки, нажмите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!

• 5

  Измерьте и запишите радиус вместе с оценкой погрешности на основе центровки.

• 6

  Теперь ваш аппарат должен быть готов к работе в максимально широком диапазоне центростремительных сил. (Почему это важно?) Центростремительную силу можно изменять, перемещая опору пружины вверх и вниз, при этом другие части устройства остаются на месте. Этот диапазон движение по центральной стойке должно быть не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.

Установка величины центростремительной силы

В этой первой части процедуры вы будете использовать метод static (без вращения) для настройки прибора на известное значение центростремительной силы.

• 1

  Присоедините зажимной шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите веревку к вращающейся массе и навесьте известную массу (начиная с 20 г) над зажимным шкивом. Отрегулируйте прижимной шкив вверх или вниз по мере необходимости так, чтобы веревка между шкивом и вращающаяся масса расположена горизонтально. (Почему это важно?)

• 2

  Запишите значение этой статической массы , которая будет определять центростремительную силу.

• 3

  Отрегулируйте опору пружины по вертикали, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора. Теперь устройство должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.

На этом этапе остановитесь и проанализируйте все силы, действующие на вращающуюся массу. Каковы их масштабы и направления? Какие-то силы не совсем вертикальные или горизонтальные? Если да, то как это повлияет на ваши результаты?

КПП 1:
Прежде чем продолжить, попросите ТА проверить ваше устройство.

Измерение периода

• 1

  Удалите статическую массу и струну из вращающейся массы. (Почему?)

• 2

  Поверните устройство, равномерно поворачивая стержень с накаткой по часовой стрелке. Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.

• 3

  Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.

• 4

  Альтернативный метод измерения среднего периода — использовать секундомер для измерения времени для N (например, 10) оборотов и разделить на N, чтобы получить T .Сделайте это хотя бы для одного испытания и сравните со значением, полученным с помощью процедуры, приведенной на шаге 3. Какой метод, по вашему мнению, более точен?

• 5

  Прежде чем продолжить, проверьте свои результаты для этой единственной точки данных и убедитесь, что ваше эмпирическое значение для вращающейся массы является разумным. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.

КПП 2:
Перед тем, как продолжить, ваш технический специалист должен проверить ваши данные и результаты расчетов.

Изменение центростремительной силы

Повторите описанную выше процедуру как минимум с пятью различными статическими массами (и, следовательно, пятью различными силами), которые охватывают максимально широкий диапазон значений (обычно от 40 до 150 г).

Анализ

• 1

  Вес статической массы, висящей на шкиве, равен центростремительной силе F , приложенной пружиной. Вычислите эту силу для каждого из пяти испытаний, умножив статическую массу на г , и запишите результаты.

• 2

  Для каждой центростремительной силы F вычислите средний период вращения T и его стандартную ошибку.

• 3

  Для каждого значения F рассчитайте ω ² и его неопределенность из

• 4

  Постройте график зависимости ω ² от F (с планками ошибок) и выполните аппроксимацию методом наименьших квадратов.

• 5

  Определите экспериментальное значение вращающейся массы, м , исходя из наклона вашего графика и уравнения центростремительной силы.Определите пересечение и линейного соответствия вашим данным. Это то, чего вы ожидаете?

Обсуждение

Сравните значение м , полученное при подборе кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть согласие в пределах неопределенностей? Если вы проведете этот эксперимент осторожно, вы сможете получить результаты с ошибкой менее 3%. Сравните значение интерцепта y с ожидаемым значением.Они согласны? Почему для этого (и большинства других) экспериментов важно получить данные в самом широком диапазоне значений? Каковы потенциальные последствия близкого расположения точек данных? Объясните, как вы собираете данные с помощью этого устройства, чтобы проверить следующую гипотезу: для данного значения центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .

Copyright © 2011 Advanced Instructional Systems, Inc. и Университет Северной Каролины | Кредиты

Вращательное движение | Блог Гэри Гарбера

До сих пор в этом семестре нашего изучения классической механики мы изучали поступательное движение. Теперь мы приступим к изучению вращательного движения.

У каждой концепции, которую мы до сих пор изучили, есть аналог вращения.

В начале года мы обсуждали, как объект может претерпеть смещение x .Мы также могли повернуть объект на угол θ.

Аналогично, скорость объекта или скорость изменения положения

имеет аналог вращения, скорость вращения, скорость изменения угла

ω = Δθ / Δt

Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости. Мы можем изучить крутящий момент, который представляет собой силу вращения. Момент инерции (или инерции вращения) — это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения.Основываясь на этом, угловой момент — это инерция вращения в состоянии вращательного движения. У нас также может быть кинетическая энергия вращения!

Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение — это исследовать период вращения, T . Измеряемый в единицах времени ( миллисекунды, секунды, часы, годы, эонов…), период — это время, необходимое для одного полного оборота. Мы также могли бы описать, как часто объект вращается.Частота объекта, f , на самом деле обратно пропорциональна периоду вращения.

T = 1 / f

и

f = 1 / т

Метрическая единица измерения частоты — герцы ( Гц, ), где 1 Гц = 1 цикла в секунду . Вы, вероятно, знакомы с термином Герц по частотам на шкале радиоприемника, например, WBUR 90,9 МГц или WBZ 1030 кГц .

Пример

Представьте, что маленький мальчик пытается вызвать головокружение, быстро вращаясь.Если он вращается с частотой 0,8 Гц, сколько времени ему потребуется, чтобы сделать 1 оборот?

f = 0,8 Гц

T = 1 / f = 1 / 0,8 Гц = 1 / 0,8 цикла в секунду = 1,25 секунды

Еще одна традиционная единица измерения частоты — оборотов в минуту или оборотов в минуту . Вы можете увидеть это на старомодном проигрывателе, который мог вращаться со скоростью 33 или 45 об / мин.

А пока рассмотрим двух маленьких человечков LEGO, стоящих на проигрывателе.Когда проигрыватель поворачивается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или скорости их вращения. Если установить проигрыватель на 45 об / мин, то оба LEGO-человечка будут иметь одинаковую скорость вращения. Однако у них разные линейные или тангенциальные скорости. Мы используем слово тангенциальный, потому что, если человек LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касающейся его кругового движения!

Мы можем рассчитать линейную скорость для каждого человека, используя уравнение

v = 2πr / т

где r — радиус круга, а T — период вращения.Помните, что скорость — это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.

Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:

Пример

f = 45 об / мин

r = 12 см

Сначала вычисляем период. С 45 об / мин = 0,75 об / с

Таким образом, период вращения равен 1.33 секунды .

Таким образом, скорость будет

v = 2πr / T = 2π (10 см ) / 1,33 с = 47 см / с

У маленького человечка, стоящего в радиусе 4 см, у него гораздо меньшая линейная скорость, хотя и такая же скорость вращения.

v = 2πr / T = 2π (4 см ) / 1,33 с = 19 см / с

Существует тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.

Мы можем определить связь между линейной скоростью и угловой скоростью с помощью следующего уравнения

v = ω r

Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.

ω = Δθ / Δt

При рассмотрении приведенного выше уравнения возникает интересный вопрос об единицах измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно было бы определить как ПОЛНЫЙ поворот на 360 °.

Вы, наверное, изучали единицы измерения углов в градусах. Но когда мы обсуждаем угловую скорость, мы обычно не говорим об целом числе оборотов. Таким образом, мы могли бы использовать такие единицы измерения, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартная единица измерения — радиан.

2π радиан = 360 °

Если мы посмотрим на изображение единичного круга, мы увидим преобразование между радианами и градусами. Это действительно одно и то же, просто разные единицы.

В каком-то смысле единственная разница между частотой и угловой скоростью заключается в единицах измерения. Угловая скорость измеряется в радианах в секунду , а частота измеряется в герцах или оборотов в секунду . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как

2πf = ω

Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об / мин.

ω = 2πf = 2π (0.75 об / с ) = 4,7 радиан / с

Пример

Давайте еще раз посмотрим на человечков LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим

v = ω r

v = 4,7 радиан / сек x 10 см = 47 см / с

и для человека ближе к центру

v = 4,7 радиан в секунду x 4 см = 19 см / с

Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом.

Веб-сайт класса физики

Круговое движение и гравитация: обзор набора задач

Этот набор из 27 задач нацелен на вашу способность комбинировать законы Ньютона и уравнения кругового движения и гравитации для анализа движения объектов, движущихся по кругу, включая орбитальные спутники.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .

Характеристики движения объектов, движущихся по кругам.

Объекты, движущиеся по кругу, имеют скорость, равную пройденному за время пути расстоянию. Расстояние вокруг круга эквивалентно длине окружности и рассчитывается как 2 • pi • R, где R — радиус.Время одного оборота по окружности называется периодом и обозначается символом T. Таким образом, средняя скорость объекта, движущегося по кругу, определяется выражением 2 • pi • R / T. Часто в постановке задачи указывается частота вращения в оборотах в минуту или в оборотах в секунду. Каждый оборот по окружности эквивалентен длине окружности. Таким образом, умножение частоты вращения на длину окружности позволяет определить среднюю скорость объекта.

Ускорение объектов, движущихся по кругу, в первую очередь зависит от изменения направления. Фактическая скорость ускорения зависит от скорости изменения направления и напрямую связана со скоростью и обратно пропорциональна радиусу поворота. В итоге ускорение определяется выражением v ² / R, где v — скорость, а R — радиус окружности.

Уравнения для средней скорости (v) и среднего ускорения (a) приведены ниже.

v = d / t = 2 • pi • R / T = частота • 2 • pi • R
а = v ² / R

Направленные величины для объектов, движущихся по кругу

Успешный математический анализ объектов, движущихся по кругу, во многом зависит от концептуального понимания направления векторов ускорения и результирующей силы. Движение по круговой траектории требует чистой силы, направленной к центру круга.В каждой точке пути результирующая сила должна быть направлена ​​внутрь. Хотя может существовать отдельная сила, направленная наружу, должна существовать внутренняя сила, которая подавляет ее по величине и удовлетворяет требованиям для внутренней чистой силы. Поскольку чистая сила и ускорение всегда в одном и том же направлении, ускорение объектов, движущихся по кругу, также должно быть направлено внутрь.

Диаграммы свободного тела и второй закон Ньютона

Часто силовой анализ должен проводиться для объекта, движущегося по кругу.Целью анализа является определение величины отдельной силы, действующей на объект, или использование значений отдельных сил для определения ускорения. Как и любая задача анализа сил, эти задачи должны начинаться с построения диаграммы свободного тела, показывающей тип и направление всех сил, действующих на объект. Из диаграммы F _net = m • можно записать уравнение. При написании уравнения помните, что сетка F _{представляет собой векторную сумму всех индивидуальных сил.Лучше всего это записывать, складывая все силы, действующие в направлении ускорения (внутрь), и вычитая те, которые ему противостоят. Два примера показаны на рисунке ниже.}

Закон всемирного тяготения Ньютона

Спутники, движущиеся по орбите, — это просто снаряды — объекты, на которые действует только сила тяжести. Сила, управляющая их движением, — это сила гравитационного притяжения к объекту, который находится в центре их орбиты.Планеты вращаются вокруг Солнца в результате гравитационной силы притяжения к Солнцу. Естественные луны вращаются вокруг планет в результате гравитационной силы притяжения к планете. Гравитация — это сила, которая действует на больших расстояниях таким образом, что любые два объекта с массой будут притягиваться. Ньютон был первым, кто предложил теорию, чтобы описать это универсальное массовое притяжение и выразить его математически. Закон, известный как закон всемирного тяготения, гласит, что сила гравитационного притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами.В форме уравнения

F _grav = G • m ₁ • m ₂ / d ²

где m ₁ и m ₂ — массы притягивающих объектов (в кг), а d — расстояние разделения, измеренное от центра объекта до центра объекта (в метрах), а G — константа пропорциональности (иногда называемая всемирная гравитационная постоянная). Значение G составляет 6,673 x 10 ^-11 Н • м ² / кг ² .

Ускорение свободного падения

Поскольку на орбитальные спутники действует исключительно сила тяжести, их ускорение является ускорением силы тяжести (g). На земной поверхности это значение составило 9,8 м / с ² . Для местоположений, отличных от поверхности Земли, необходимо уравнение, которое выражает g через соответствующие переменные. Ускорение свободного падения зависит от массы объекта, который находится в центре орбиты (M _{центральный} ) и расстояния разделения от этого объекта (d).Уравнение, связывающее эти две переменные с ускорением свободного падения, получено из закона всемирного тяготения Ньютона. Уравнение

g = G • M _{центральный} / d ²

где G составляет 6,673 x 10 ^-11 Н • м ² / кг ² .

Орбитальная скорость

Скорость, необходимая для того, чтобы спутник оставался на орбите вокруг центрального тела (планеты, солнца, другой звезды и т. Д.).) зависит от радиуса орбиты и массы центрального тела. Уравнение, выражающее взаимосвязь между этими переменными, получается путем объединения определений ускорения кругового движения с законом всемирного тяготения Ньютона. Уравнение

v = SQRT (G • M _{центральный} / R)

где M _central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, G — 6,673 x 10 ^-11 Н • м ² / кг ² .

Орбитальный период

Для общего движения объекта по кругу период связан с радиусом круга и скоростью объекта уравнением v = 2 • pi • R / T. В случае орбитального спутника это уравнение для скорости можно приравнять к уравнению для орбитальной скорости, полученной из всемирного тяготения, чтобы получить новое уравнение для орбитального периода. Результат вывода —

T ² / R ³ = 4 • pi ² / (G • M _{центральный} )

где M _central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6.673 x 10 ^-11 Н • м ² / кг ² . Выраженное таким образом уравнение показывает, что отношение квадрата периода к радиусу в кубе для любого спутника, вращающегося вокруг центрального тела, одинаково независимо от природы спутника или радиуса его орбиты. Это соотношение зависит только от массы объекта, который втягивает орбитальный спутник внутрь. Этот принцип согласуется с третьим законом движения планет Кеплера.

Резюме математических формул

Одна из трудностей, с которыми может столкнуться учащийся в этом наборе задач, — это путаница относительно того, какую формулу использовать.В таблице ниже представлено полезное резюме формул, относящихся к круговому движению и движению спутника. В таблице многие формулы получены из других уравнений. Таким образом, часто будет несколько способов определения неизвестной величины. Подходя к этим проблемам, рекомендуется практиковать обычные привычки эффективного решателя проблем; определить известные и неизвестные величины в виде символов физических формул, наметить стратегию использования известных для решения неизвестного, а затем, наконец, выполнить необходимые алгебраические шаги и замены, необходимые для решения.

Для расчета …	… используйте уравнение (а):
Скорость (v)	v = 2 • pi • R / T v = SQRT (G • M центральный / R) только для спутников
Разгон (а)	a = v 2 / R или a = F net / m a = g = G • M центральный / d 2 только для спутников
Чистая сила (F net )	F net = m • a или F net = m • v 2 / R F net = F grav = G • m sat • M центральный / d 2 только для спутников
Период (Т)	T = 2 • pi • R / v T 2 = 4 • pi 2 / (G • M центральный ) • R 3 только для спутников

Привычки эффективно решать проблемы

Эффективный решатель проблем по привычке подходит к физическим проблемам таким образом, чтобы отражать набор дисциплинированных привычек.Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …

• … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
• … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме.Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, m = 61,7 кг, v = 18,5 м / с, R = 30,9 м, F _norm = ???).
• … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
• … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
• … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.

Подробнее …

Дополнительная литература / Учебные пособия:

Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.

Набор задач кругового движения и гравитации

Просмотреть набор задач

Решения с аудиогидом для кругового движения и гравитации

Просмотрите решение проблемы с аудиогидом:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27

об / мин vs.Угловая скорость | Sciencing

Число оборотов в минуту (об / мин) и угловая скорость, два показателя скорости вращения точки относительно другой точки, используются для решения задач физики, машиностроения и компьютерного программирования. Часто обороты и угловая скорость взаимозаменяемы для имитации вращения шкивов и качения колес в инженерных симуляторах и видеоиграх.

Использование угловой скорости

Угловая скорость используется для выражения скорости вращения круглого объекта, например колеса.Поскольку круг состоит из 360 градусов, колесо, которое совершает один полный оборот вокруг своего центра за одну секунду, будет иметь угловую скорость 360 градусов в секунду. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 60 секунд, она имеет угловую скорость 360 градусов каждые 60 секунд или 6 градусов в секунду.

Число оборотов в минуту Использует

Число оборотов в минуту также используется для выражения скорости вращения круглого объекта, такого как колесо.Поскольку один оборот эквивалентен одному полному обороту или вращению вокруг центральной точки, говорят, что колесо, которое совершает один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в минуту или 1 оборот в минуту. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 1 минуту, ее скорость вращения составляет 1 оборот в минуту или 1 оборот в минуту.

Преобразование угловой скорости в число оборотов в минуту

Угловая скорость в градусах в секунду может быть преобразована в число оборотов в минуту путем умножения угловой скорости на 1/6, поскольку один оборот составляет 360 градусов, а это 60 секунд в минуту.Если угловая скорость задана как 6 градусов в секунду, число оборотов в минуту будет 1 оборот в минуту, поскольку 1/6, умноженное на 6, дает 1.

об / мин Преобразование угловой скорости

Оборотов в минуту можно преобразовать в угловую скорость в градусов в секунду, умножив число оборотов на 6, так как один оборот составляет 360 градусов, а это 60 секунд в минуту. Если частота вращения равна 1 об / мин, угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6 умноженное на 1 равно 6.

6.1 Угол вращения и угловая скорость — Физика

Цели обучения разделу

К концу этого раздела вы сможете делать следующее:

• Опишите угол поворота и соотнесите его с его линейным аналогом
• Опишите угловую скорость и свяжите ее с ее линейным аналогом
• Решение задач, связанных с углом поворота и угловой скоростью

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:

• (4) Научные концепции.Учащийся знает и применяет законы движения в различных ситуациях. Ожидается, что студент:
  • (C) анализировать и описывать ускоренное движение в двух измерениях с помощью уравнений, включая примеры снарядов и кругов.

Раздел Основные термины

Угол поворота

Что именно мы подразумеваем под круговым движением или вращением ? Вращательное движение — это круговое движение объекта вокруг оси вращения.Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, разгоняющийся по круговой кривой, игрушку, прикрепленную к веревке, раскачивающуюся по кругу вокруг вашей головы, или круглый loop-the-loop на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, вращение Земли вокруг своей оси, вращение колеса на своей оси, вращение торнадо на его пути разрушения или фигурист, вращающийся во время выступление на Олимпиаде.Иногда объекты будут вращаться во время кругового движения, как Земля вращается вокруг своей оси при вращении вокруг Солнца, но мы сосредоточимся на этих двух движениях по отдельности.

Поддержка учителей

Поддержка учителей

[BL] [OL] Объясните разницу между круговыми и вращательными движениями, используя вращение Земли вокруг своей оси и ее вращение вокруг Солнца. Объясните, что вращение Земли немного эллиптическое, хотя почти круглое.

[OL] [AL] Попросите студентов придумать примеры кругового движения.

При решении задач, связанных с вращательным движением, мы используем переменные, которые аналогичны линейным переменным (расстояние, скорость, ускорение и сила), но учитываем кривизну или вращение движения. Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловым эквивалентом линейной скорости.

Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск на рисунке 6.2 вращается вокруг своего центра — каждая точка в объекте следует по круговой траектории.

Рис. 6.2. Все точки на компакт-диске движутся по круговой траектории. Ямки (точки) вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.

Длина дуги , — это расстояние, пройденное по круговой траектории. Радиус кривизны r — это радиус круговой траектории. Оба показаны на рисунке 6.3.

Рис. 6.3 Радиус ( r ) окружности повернут на угол ΔθΔθ. Длина дуги ΔsΔs — это расстояние, пройденное по окружности.

Рассмотрим линию от центра компакт-диска до его края. За заданное время каждая яма (используемая для записи информации) на этой линии перемещается на один и тот же угол. Угол поворота — это величина вращения, являющаяся угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.

Угол поворота часто измеряется в радианах. (Радианы на самом деле безразмерны, потому что радиан определяется как отношение двух расстояний, радиуса и длины дуги.) Оборот — это один полный оборот, при котором каждая точка круга возвращается в исходное положение. Один оборот охватывает 2π2π радиан (или 360 градусов) и, следовательно, имеет угол поворота 2π2π радиан и длину дуги, равную длине окружности. Мы можем преобразовывать радианы, обороты и градусы, используя соотношение

1 оборот = 2π2π рад = 360 °. См. Таблицу 6.1 для преобразования градусов в радианы для некоторых распространенных углов.

2π рад = 360 ° 1рад = 360 ° 2π≈57.3 ° 2π рад = 360 ° 1рад = 360 ° 2π≈57,3 °

6,1

Градус Меры	Меры радиана
30-30 °	π6π6
60∘60∘	π3π3
90∘90∘	π2π2
120–120–	2π32π3
135∘135∘	3π43π4
180∘180∘	ππ

Таблица 6.1 Обычно используемые углы в градусах и радианах

Угловая скорость

Поддержка учителя

Поддержка учителя

[BL] Проверьте смещение, скорость, скорость, ускорение.

[AL] Спросите студентов, изменяется ли скорость при равномерном круговом движении. А как насчет скорости? А как насчет разгона?

Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Рассмотрим сначала угловую скорость (ω) (ω) — это скорость, с которой изменяется угол поворота.В форме уравнения угловая скорость равна

ω = ΔθΔt, ω = ΔθΔt,

6,2

, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).

Теперь давайте рассмотрим направление угловой скорости, что означает, что теперь мы должны называть ее угловой скоростью. Направление угловой скорости — вдоль оси вращения.Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.

Угловая скорость (ω) — это угловая версия линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске.Эта яма движется по длине дуги (Δs) (Δs) за короткий промежуток времени (Δt) (Δt) (Δt) (Δt), поэтому его тангенциальная скорость равна

Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs ​​= rΔθ. Подставляя это в выражение для v , получаем

v = rΔθΔt = rω. v = rΔθΔt = rω.

Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае CD (с большим r ), чем для точки ближе к центру CD (с меньшим r ).Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрыть большую длину дуги за то же время, что и точка ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.

Рисунок 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она дальше от центра вращения.

Teacher Support

Teacher Support

[AL] Объясните, что период времени ΔtΔt в уравнении, определяющем тангенциальную скорость (v = ΔsΔtv = ΔsΔt), должен быть коротким, чтобы дугу, описываемую движущимся объектом, можно было приблизительно представить как прямую. линия.Это позволяет нам определить направление касательной скорости как касательное к окружности. Это приближение становится все более точным по мере того, как ΔtΔt становится все меньше и меньше.

Теперь рассмотрим другой пример: шину движущегося автомобиля (см. Рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое v , потому что v = rωv = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать для автомобиля большую линейную (тангенциальную) скорость v, .Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.

Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом и колеса вращались, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r — радиус шины.Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Чем больше угловая скорость шины, тем больше линейная скорость автомобиля.

Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шины, больше, чем линейное расстояние, по которому движется автомобиль.Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.

Советы для успеха

Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление. Направление угловой скорости — вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки.Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.

Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена ​​по касательной к кругу. Направление угловой скорости в данном случае указано на странице.

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью.Здесь также показано, как преобразовать число оборотов в радианы.

Проверка захвата

Для объекта, движущегося по круговой траектории с постоянной угловой скоростью, изменится ли линейная скорость объекта при увеличении радиуса пути?

1. Да, потому что тангенциальная скорость не зависит от радиуса.
2. Да, потому что тангенциальная скорость зависит от радиуса.
3. Нет, поскольку тангенциальная скорость не зависит от радиуса.
4. Нет, потому что тангенциальная скорость зависит от радиуса.

Решение задач, связанных с углом вращения и угловой скоростью

Snap Lab

Измерение угловой скорости

В этом упражнении вы будете создавать и измерять равномерное круговое движение, а затем сравнивать его с круговыми движениями с разными радиусами.

• Одна струна (длина 1 м)
• Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
• Один таймер

Процедура

1. Привяжите объект к концу строки.
2. Поверните объект по горизонтальному кругу над головой (замахиваясь запястьем). Важно, чтобы круг был горизонтальным!
3. Удерживайте объект на постоянной скорости во время качания.
4. Измерьте таким образом угловую скорость объекта. Измерьте время в секундах, за которое объект совершит 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
5. Какова приблизительная линейная скорость объекта?
6. Переместите руку вверх по тетиве так, чтобы ее длина составляла 90 см.Повторите шаги 2–5.
7. Переместите руку вверх по струне так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
8. Переместите руку вверх по струне так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
9. Переместите руку вверх по струне так, чтобы ее длина составила 60 см. Повторите шаги 2–5
.
10. Переместите руку вверх по струне так, чтобы ее длина составила 50 см. Повторите шаги 2–5
.
11. Постройте графики зависимости угловой скорости от радиуса (т. Е. Длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.

Проверка захвата

Если вы поворачиваете объект медленно, он может вращаться со скоростью менее одного оборота в секунду. Какими были бы обороты в секунду для объекта, который совершает один оборот за пять секунд? Какова была бы его угловая скорость в радианах в секунду?

1. Объект будет вращаться в \ frac {1} {5} \, \ text {rev / s}. Угловая скорость объекта будет \ frac {2 \ pi} {5} \, \ text {rad / s}.
2. Объект будет вращаться в \ frac {1} {5} \, \ text {rev / s}.Угловая скорость объекта будет \ frac {\ pi} {5} \, \ text {rad / s}.
3. Объект будет вращаться со скоростью 5 \, \ text {rev / s}. Угловая скорость объекта будет 10 \ pi \, \ text {rad / s}.
4. Объект будет вращаться со скоростью 5 \, \ text {rev / s}. Угловая скорость объекта будет 5 \ pi \, \ text {rad / s}.

Теперь, когда у нас есть понимание понятий угла поворота и угловой скорости, мы применим их к реальным ситуациям с часовой башней и вращающимся колесом.

Рабочий пример

Угол поворота часовой башни

Часы на часовой башне имеют радиус 1,0 м. (a) На какой угол поворота движется часовая стрелка часов, когда она движется с 12 часов дня. до 15:00? (б) Какова длина дуги по внешнему краю часов между часовой стрелкой в ​​эти два момента времени?

Стратегия

Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрытых часовой стрелкой при переходе от 12 к 3.Когда у нас есть угол поворота, мы можем найти длину дуги, переписав уравнение Δθ = ΔsrΔθ = Δsr, поскольку радиус задан.

Решение для (а)

При переходе с 12 на 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в ​​точках 12 и 3 равен 14 × 2πrad = π214 × 2πrad = π2 (т.е. 90 градусов).

Решение к (b)

Преобразование уравнения

получаем

Вставка известных значений дает длину дуги

Δs = (1.0 м) (π2рад) = 1,6 м Δs = (1,0 м) (π2рад) = 1,6 м

6,6

Обсуждение

Нам удалось отбросить радианы из окончательного решения в часть (b), потому что радианы на самом деле безразмерны. Это потому, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.

Рабочий пример

Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость 0.Автомобильная шина с радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 6.5.

Стратегия

В этом случае скорость протектора шины по отношению к оси шины такая же, как и скорость автомобиля по отношению к дороге, поэтому мы имеем v = 15,0 м / с. Радиус покрышки r = 0,300 м. Поскольку мы знаем v и r , мы можем переписать уравнение v = rωv = rω, чтобы получить ω = vrω = vr и найти угловую скорость.

Решение

Чтобы найти угловую скорость, воспользуемся соотношением: ω = vrω = vr.

Вставка известных величин дает

ω = 15,0 м / с 0,300 м = 50,0 рад / с. ω = 15,0 м / с 0,300 м = 50,0 рад / с.

6,7

Обсуждение

Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с (то есть 50,0 в секунду, что обычно записывается как 50,0 с ^-1 ). Но угловая скорость должна иметь единицы рад / с. Поскольку радианы безразмерны, мы можем вставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если землеройный трактор с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его шины вращались медленнее. У них будет угловая скорость

ω = 15,0 м / с 1,20 м = 12,5 рад / с ω = 15,0 м / с 1,20 м = 12,5 рад / с

6,8

Практические задачи

1.

Какой угол в градусах между часовой и минутной стрелками часов, показывающих 9:00 утра?

1. 0 °
2. 90 °
3. 180 °
4. 360 °

2.

Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00 a.м, если радиус часов 0,2 м?

1. 0,1 м
2. 0,2 м
3. 0,3 м
4. 0,6 м

Проверьте свое понимание

3.

Что такое круговое движение?

1. Круговое движение — это движение объекта по линейной траектории.
2. Круговое движение — это движение объекта по зигзагообразной траектории.
3. Круговое движение — это движение объекта по круговой траектории.
4. Вариант D сбивает с толку как отвлекающий фактор

4.

Что подразумевается под радиусом кривизны при описании вращательного движения?

1. Радиус кривизны — это радиус круговой траектории.
2. Радиус кривизны — это диаметр круговой траектории.
3. Радиус кривизны — это длина окружности круговой траектории.
4. Радиус кривизны — это площадь круговой траектории.

5.

Что такое угловая скорость?

1. Угловая скорость — это скорость изменения диаметра круговой траектории.
2. Угловая скорость — это скорость изменения угла, образованного круговой траекторией.
3. Угловая скорость — это скорость изменения площади круговой траектории.
4. Угловая скорость — это скорость изменения радиуса круговой траектории.

6.

Какое уравнение определяет угловую скорость ω, когда r — радиус кривизны, θ — угол, а t — время?

1. \ omega = \ frac {\ Delta \ theta} {\ Delta {t}}
2. \ omega = \ frac {\ Delta {t}} {\ Delta \ theta}
3. \ omega = \ frac {\ Delta {r}} {\ Delta {t}}
4. \ omega = \ frac {\ Delta {t}} {\ Delta {r}}

7.

Назовите три примера объекта, совершающего круговое движение.

1. Искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
2. Искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и мяч, привязанный к веревке, вращающейся по кругу вокруг головы человека
3. Земля вращается вокруг своей оси, гоночный автомобиль движется по круговой гоночной трассе, и мяч, привязанный к веревке, вращается по кругу вокруг головы человека
4. Земля, вращающаяся вокруг своей оси, лопасти работающего потолочного вентилятора и волчок, вращающийся вокруг собственной оси

8.

Какова взаимная ориентация радиуса и векторов тангенциальной скорости объекта при равномерном круговом движении?

1. Вектор тангенциальной скорости всегда параллелен радиусу круговой траектории, по которой движется объект.
2. Вектор тангенциальной скорости всегда перпендикулярен радиусу круговой траектории, по которой движется объект.
3. Вектор тангенциальной скорости всегда находится под острым углом к ​​радиусу круговой траектории, по которой движется объект.
4. Вектор тангенциальной скорости всегда находится под тупым углом к ​​радиусу круговой траектории, по которой движется объект.

Teacher Support

Teacher Support

Используйте вопросы Check Your Understanding , чтобы оценить, усвоили ли учащиеся учебные цели этого раздела. Если учащиеся борются с определенной целью, формирующая оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.

Решение задач угловой скорости — Precalculus

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Скорость вращения — видео по физике от Brightstorm

Скорость, с которой объект вращается или вращается, называется скоростью вращения .В отличие от линейной скорости, она определяется количеством вращений объекта за период времени. Формула для скорости вращения: Скорость вращения = число оборотов / время , но линейная скорость = расстояние / время .

Хорошо, давайте поговорим о скорости вращения, скорость вращения действительно состоит из двух компонентов. Один из них — это линейная скорость, которую также называют тангенциальной скоростью, и это, по сути, расстояние, на котором объект движется с течением времени, нормально.Если он движется по круговой орбите, если мы выпустим его с этой орбиты, он продолжит движение по касательной от этой точки с определенной скоростью, нормально. Другая скорость объекта — это скорость вращения, скорость вращения — это количество оборотов за раз. Итак, давайте рассмотрим пример, вас часто спрашивают: допустим, у нас есть 2 точки на записи, и рекорд вращается с определенной скоростью, например, 33 оборота в минуту, хорошо. Что ж, если мы сравним скорость этих двух объектов, она будет очень разной, если мы говорим о тангенциальной, линейной или тангенциальной скорости относительно скорости вращения.Итак, если мы посмотрим на них обоих, они оба имеют скорость вращения 33 оборота в минуту.

Но если мы посмотрим на скорость, с которой они движутся на записи, на линейную скорость, мы увидим, что линейная скорость на самом деле связана с радиальным расстоянием по сравнению со скоростью вращения. Итак, если я скажу, что a равно x, а b равно 2x с точки зрения нашего радиального расстояния, расстояния с точки зрения радиуса от центра справа, мы увидим, что b будет двигаться намного быстрее, чем a. Вот почему 2 объекта могут иметь одинаковую скорость вращения, но очень разные линейные скорости.

.

No related posts.