Сопротивление проволоки, как узнать электрическое сопротивление провода, шнура, кабеля.

В области электротехники, электроники понятие электрического сопротивления является фундаментальным. Оно относится к основным электрическим величинам, которое повсеместно используется как в теории, так и на практике. Любой электрический проводник имеет свое определенное сопротивление, которое во многом зависит от таких основных факторов: материала проводника, его размер (длина и сечение), температура. Помимо этого стоит учитывать, что сопротивление может быть активным и реактивным.

Электрическое сопротивление провода можно вычислить по следующей простой формуле, в которой присутствуют такие величины: удельное сопротивление материала, из которого сделан провод, его сечение и длина:

Есть такое понятие как удельное сопротивление материала (вещества). У каждого проводника, сделанного из того или иного материала свое удельное сопротивление. Это обуславливается особенностями внутренней структуры (на атомном уровне) самого вещества. То есть, у каждого отдельно взятого материала (проводника тока) при одних и тех же размерах и условиях будет различное сопротивление. Это удельное сопротивление выражается как Ом на метр (при сечении 1 миллиметр квадратный). Удельное сопротивление каждого отдельного материала проводника нужно смотреть в специальной таблице (в справочниках, интернете).

Нахождением сопротивления по формуле имеет смысл при теоретических расчетах, на практике же намного проще воспользоваться обычным измерителем (электронным тестером, мультиметром, омметром). Стоит учитывать, что измерения электрического сопротивления должны производиться при отключенном электропитании схемы, участка цепи, провода. Если на схеме (измеряемом проводе) будет присутствовать хоть какое-то напряжение, то в лучшем случае это повлечет за собой неверные результаты измерения, ну, а в худшем может выйти из строя и сам измерительный прибор.

Само же измерение электрического сопротивления мультиметром сводится к его включению и выбору на нём определённого диапазона измерения (Ом, килоОм, мегаОм). Наиболее малым сопротивлением является Ом. 1000 Ом, это 1 кОм (килоом). 1000 000 Ом или 1000 кОм, это 1 мОм (мегаом). В обычных проводах (шнуры питания, небольшие куски кабеля и проводов) сопротивление будет примерно до десятков Ом. Сопротивление от десятков и до тысяч Ом уже можно встретить к примеру у обмоток трансформатора, катушек электромагнита, звонка и т.д. Ну, а мегаомным сопротивлением уже обладает электрическая изоляция кабелей и проводов.

В электротехнике в большинстве случаев в роли электрического проводника используют медь. Именно она имеет достаточно хорошую электрическую проводимость при относительно низкой цене (если сравнивать с серебром, золотом). В линиях электропередач и на отдельных участках бытовой электросети также широко применяют алюминий, хотя его электрическая проводимость хуже, чем у меди, зато стоит меньше. И медь и алюминий (если говорить о сопротивлении небольших участков электрической сети, кабеля и шнуры питания) имеет электрическое сопротивление в пределах единиц и десятков Ом. Ну, естественно, чем длиннее и тоньше будет проводник, тем сопротивление будет увеличиваться (допустим у трансформаторной первичной обмотки на 220 вольт сопротивление уже от десятков до нескольких тысяч Ом, в зависимости от мощности транса).

Для чего может, собственно, пригодится известная величина электрического сопротивления? Наиболее используемой в электрике и электронике является формула закона Ома. Она гласит, что сила тока равна электрическое напряжение разделенное на сопротивление. Следовательно, зная любые две величины из трех (тока, напряжения и сопротивления) можно всегда найти одну неизвестную. К примеру, нам нужно узнать, какой ток будет протекать по спирали нагревателя. Нам известно, что этот нагреватель рассчитан на напряжение 220 вольт. Берём мультиметр и измеряем его сопротивление (допустим это 100 Ом). Используя формулу закона Ома мы легко вычислим силу тока: 220 вольт / 100 Ом = 2,2 ампера.

P.S. При нахождении электрического сопротивления через формулу учитывайте, что реальные величины могут слегка отличаться от теоретических (по причине материальных факторов, условий окружающей среды и т. д.). При нахождении сопротивления путем простого измерения учитывайте, что измерительные приборы имеют свою погрешность (хоть она и достаточно мала, но всё же есть).

Примеры на расчет сопротивления проводника, силы тока и напряжения

на прошлом уроке мы выяснили от чего зависит сопротивление проводника ну теперь давайте порешаем задачи на вычисление этого самого сопротивления термо задачи на вычисление сопротивления проводника задачи на вычисление сопротивления проводника начнем с задачей номер один а высокого уровня страница 119 кирик номер один а высокого уровня страница 119 кирик домашнее задание мы уже записали на прошлом уроке эта задача на самом деле на высокий уровень не тянет просто тут под одним номером несколько задач и но нас интересует только 1 1 на катушку электромагнита намотан медный провод сечением три сотых квадратного миллиметра и длиной 200 метров и то есть площадью поперечного сечения с 0 0 3 миллиметра квадратного найдите сопротивление и массу обмотки на катушку электромагнита намотан медный провод сечением и длиной l равняется 200 метров найдите сопротивление и массу обмотки какие характеристики материала в нашем случае меди нам нужны для решения этой задачи андрей отлично какой буквой обозначается плотность роб какой буквой обозначается удельное сопротивление ро для того чтобы не путать эти две величины давайте воспользуемся таким это делать просто предлагаю таким сокращением если эта плотность от него от нее зависит масса обозначим ее роз индексом м а если это удельное сопротивление от него от удельного сопротивления зависит сопротивление обозначим его роз индексом n поскольку сопротивление обозначаются большой или маленькой буквой r и из справочника можно записать плотность меди 8900 килограммов на метр кубический а удельное сопротивление меди 1 из 7 на 10 в минус восьмой он на метр нужно найти массу проводника андрей пожалуйста доске и нужно найти сопротивление проводника объем не спеши не торопись масса делить на объем так отсюда можем найти массу как вырази отсюда массу роз индексом м маленькую букву м чтобы мы не думали что это сомножитель у нас есть тряпка так хорошо что такое в в это объем который вычисляется умножением длины на площадь поперечное сечение так можем сразу записать рабочую формулу для нахождения массы проводника так уберем ее в рамочку теперь нам нужно найти сопротивление этого проводника на что zara роз индексом р-на или что такое на умножить на dy делить на вес так у нас все есть что нужно все уберем в рамку так теперь главное не ошибиться при вычислениях давай начнем с массой до 10 2 метра хорошо длина дальше так интересно как это у тебя получилось значит это 3 на 10 минус 2 метра здесь минус 3 в квадрате совершенно верно и три на десять в минус 8 метра квадратного старайся писать аккуратней такого же и еще у нас плотность ну давай уже в таком же стиле 8,9 на 10 чего килограммов делить на метр кубический ответ будет в килограммах как вы думаете много этих килограммов будет тоненький провод очень тонкие поэтому давайте если по дороге где-то встретиться 10 минус 3 оставим ее для того чтобы вместе с килограммом эти 10 минут 3 дали нам грамма будем это иметь в виду 2 5 так здесь отлично значит вот это все заменяем на нет ну так не совсем красиво для себя это можно но на зрителя лучше такие вещи не демонстрировать вот 10 минус 3 килограмма вот теперь эти 10 минут три килограмма бонус сохранять грамм и до ответ уже будет у нас в граммах вот те калькулятор примерно 50 ты примерно 50 лет там пятьдесят три четыре десятых но мы берем 2 значащих цифр и хотя бы потому что у нас плотности удельное сопротивление указаны с точностью до двух значащих цифр так сопротивление нам нужно удельное сопротивление это переведем его сразу не будем все писать тут у нас будет ноль ишь ты как быстро хорошо тогда правильно- единицы запиши так отлично 003 здесь вы видите миллиметры квадратные сокращаются метры сокращаются здесь написать 1 из 7 а там зачеркну 20 а так это будет что у нас 172 значит 3,4 до делить на ноль ноль посчитать 3,4 разделить на 0 03 113 приблизительно 113 кому можно было бы сократить округлить до двух значит до двух значащих цифр но так как первая цифра единиц а можно оставить три единственное что вот стань стороночку это случайно не тысячу сто тридцать метров нет значит для того чтобы вот такие вещи не возникали нужно либо оставлять промежуток какой то заметны либо писать цифру цифра 0 обычно пишет худенькая буква вот такая жир не но самое милое дело это просто сделать пробел спасибо андрей и так сопротивление 113 он масса 53 грамма следующая задача тоже из кирико номер 4 а высокого уровня страница 120 номер 4 а высокого уровня страница 120 кирик нужно изготовить провод длиной 100 метров и сопротивлением 1 ом в каком случае провод получится легче если его сделать из алюминия или из меди во сколько раз легче нужно изготовить провод длиной 100 метров и сопротивлением 1 ом дети как я пишу 1 у какие 0 и здесь и какая буква а здесь в каком случае провод получится легче если его сделать из алюминия или из меди и во сколько раз то есть надо найти отношение масс ну давайте массу медного провода обозначим м купрум поделим на массу алюминиевого провода м алюминий какие нам понадобятся справочные данные так андрей удельное сопротивление плотности ролла алюминия равняется 2 тысячи 700 килограммов на метр кубический плотность алюминия рот м меди равняется 8900 килограмм на метр кубический р-р алюминия равняется кажется 28 до 2 и 8 на 10 минус 8 2 и 8 на 10 минус 8 умножить на метр r кубе равняется 1 и 7 на 10 минус 8 ом на метр вот все справочные данные у нас есть за что зацепиться ну раз спрашивают отношение масс давайте выразим массу через плотность длину кстати длина известно на 1 этаже обоих проводников и площадь поперечного сечения его у нас нет ну посмотрим что будет дальше итак масса равняется плотности rock n умножить на длину и умножить на площадь поперечного сечения эта формула работает и тогда когда мы берем проводник из меди и тогда когда мы берем проводник из алюминия поэтому эту формулу можно записать дважды длина будет одна и та же а площади поперечного сечения наверно разные поэтому напишем так масса медного провода равняется х м купрум умножить на k l длина 1 этаже поэтому индексов никаких не ставим умножить на cos kuprum аналогично масса алюминиевого провода равняется р о м алюминиевом алюминия на u и умножить на с колю менее вот так делим одно на другое масса провода из меди и делить на массу проводах из алюминия равняется посмотрите сюда у нас сократится длина значит сразу не будем ее писать останется в числителе плотность роем меди умножить на площадь поперечного сечения медного провода и в знаменателе аналогично плотность руфинг алюминия делить на площадь поперечного сечения алюминиевого провода условие задачи нет площадей поперечного сечения проводов но давайте посмотрим что мы еще не использовали мы не использовали формулу для сопротивления а сопротивления у нас есть в условии задачи вспомним сопротивление r мы получим если удельное сопротивление роз индексом n умножим на длину и разделен на площадь поперечного сечения эту формулу мы можем применить как для алюминиевого провода так и для медного для алюминия р но одно и то же поэтому индексы писать не будем равняется р о р алюминия умножить на длину она у обоих проводов одинаково поэтому яндекс тоже не будем ставить делить на площадь поперечного сечения алюминия с алюминия тоже самое можно записать для медного провода то же самое 1 умное сопротивление мы получим если удельное сопротивление меди умножим на длину и разделим на площадь поперечного сечения медного провода теперь наверно можно приравнять эти два сопротивления и у нас получится rocher алюминия умножить на n разделить на площадь lumia равняется рокер меди умножить на х и разделить на с миди длина сократится а теперь смотрите здесь нам для решения задачи надо знать отношения площади медного провода к площади алюминиевого его отсюда можно выразить для этого вот это с купрум перегоним сюда в числитель а удельное сопротивление алюминия запишем справа в знаменатель у нас получится с купрум делить на из алюминия равняется из круп купим здесь ро rq пром в числителе роя алюминия в знаменателе и теперь вот это мы заменяем на вот это это отношение равно отношению удельных сопротивлений у нас получается масса медного провода так относится к массе алюминиевого провода как плотность меди умножить на удельное сопротивление меди разделить на плотность алюминия и удельное сопротивление алюминия вот рабочая формула остается провести расчет ой считаем масса меди на масса алюминия равняется дробь и здесь о единицах можно вообще не задумываться лишь бы они были одинаковые плотность меди 8900 удельное сопротивление медиа я пишу просто 1 из 7 здесь за единицу и принимает 10 минус 8 вам метр делить на 2700 и на 2 и 8 эти два нолика можно сократить получается приблизительно 2 причем с хорошей точностью до 2 итак два интересных факта первое медный провод вдвое тяжелее аллюминиевого второй интересный факт нам не понадобилась не значение сопротивления не значения длины второе впрочем совершенно не удивительно какая разница какой у нас проводник такой или километровый если у них одинаковое сопротивление у двух медных такой длины или u2 медного и алюминиевого километровой длины отношение масс все равно будет одно и то же эти числа приведены для того чтобы те кто не умеет решать задачи в общем виде тоже могли добраться до ответа но поскольку наш стиль немножко не такой по нам не нужно эти данные использовать мы вполне обходимся без этого медный провод в два раза массивней это значит что если вы изготавливаете линию электропередач то лучше ее делать из алюминия потому что тогда опоры не нужно делать такими прочными правда я не знаю что дороже алюминия или медь они наверно примерно одинаковой цене потому что это это приходится получать по сходным технологиям необходимо огромное количество электроэнергии для того чтобы получить электротехническую медь и для того что получить электротехнические алюминий правда есть одно но алюминий не такой прочный как ведь знаете что делают для того чтобы алюминиевые провода не порвались на линии электропередач середине провода которым прокладывают воздушные линии электропередач которую вешают на пор идут стальные жилки оцинкованная стальная проволока она обеспечивает высокую прочность проводника линий электропередач алюминий сверху его больше обеспечивает хорошую электропроводность то есть низкое сопротивление и там стандартное сопротивление линии электропередачи вчера просто в проводах в справочник по проводам в google и посмотрел две десятых ома на километр вот обычные провода линии электропередач которой висят на столбах те что мне попались две десятых ума на километр это очень не высокое сопротивление следующая задача следующая задача давайте такую задачу решил она приведет нас к интересному соотношению задача номер 3 б высокого уровня номер 3 б высокого уровня ребята открывайте тетради по теории 3b высокого уровня страница 122 это будет такая демонстрационная задач которая приведет нас к интересному соотношению берем тетради по теории пишем 3 б высокого уровня страница 122 какова напряженность поля в алюминия вам проводнике сечением один квадратный миллиметр при силе тока 1 ампер какова напряженность поля в алюминия вам проводники сечением с 1 целое 4 десятых квадратного миллиметра при силе тока 1 ампер нужно найти напряженность поля за что тут зацепиться ну давайте так алюминий что мы о нем знаем мы знаем его удельное сопротивление если мы знаем удельное сопротивление а тут еще указывается площадь поперечного сечения наверное нам поможет формулы для вычисления сопротивления проводника r равняется 2 умножить на n делить на площадь поперечного сечения площадь поперечное сечение известно теперь давайте дальше рассуждать нам известна сила тока в проводнике в принципе мы можем обсуждать также сопротивление проводника что мы получим если силу тока умножим на сопротивлением напряжение давайте вспомним закон ома по закону ома сила тока в однородном участке цепи а у нас это так прямо пропорциональна напряжению и обратно пропорциональна противление отсюда мы можем найти напряжение равняется и r одна из форм записи закона ома сила тока до на сопротивление мы посчитаем сейчас по крайней мере выйдем на него значит мы можем записать напряжение равняется силе тока и умножить на сопротивление народ ноэль делить на с проводник на его концах разность потенциалов моё почти нашли мы только вот длины не знали длина проводника нам надо найти напряженность поля в нем в проводнике как и уёк найти по вот этой формуле е равен а у делить на расстоянии до какое расстояние у нас и так а теперь возникает вопрос скажите пожалуйста а когда эта формула работает когда какое электрическое поле когда поле однородная а можем ли мы это непростой вопрос можем ли мы считать поле внутри проводника однородная вот например представьте себе у вас источник тока на одном конце избыток положительных зарядов на другом избыток отрицательных зарядов допустим это два точечных заряда между ними поле будет однородная ни в коем случае ближе к зарядам напряженность больше посерединке напряженность поменьше а эта формула работает только для однородного поля можем ли мы и так сразу раз и использовать нужны какие-то слова какие-то аргументы в пользу того что поле в проводнике можно считать однородным ток постоянный хорошо значит сила тока не зависит от времени добры скажите пожалуйста через вот это поперечное сечение и через вот это поперечное сечение каждую секунду один заряд проходит один иначе бы заряды где-то накапливались но они не накапливаются проходят сквозь значит скорость движения зарядов везде одинаково значит в среднем если все заряды движутся в среднем равномерно reach you tube средней скорости то сила действующая на заряды и здесь и здесь и одна и та же в среднем но ведь это и означает что напряженность поля везде здесь одна и та же поэтому мы можем считать что поле однородно то есть на самом деле действительно задача решается очень просто итак это формула действительно может быть использована напряжение мы знаем и мы можем записать чему равняется напряженность подставляем вот это напряжение сюда и у нас получается напряженность поля равна и рок-н делить на с и вот на эту длину и длина провода у нас сократится и у нас получается напряженность поля равняется х умножить на силу тока и разделить на площадь вот рабочие формула проведем расчеты я равняется провод у нас какой алюминиевый значит из таблиц в рок равняется 2 и 8 на 10 в минус 8 ом умноженный на метр и тогда напряженность поля равняется 2 и 8 на 10 минус 8 ом на метр умножить на 1 ампер и разделить на 1 и 4 на 10 андрей подсказывай минус 6 метров квадрата так хорошо равняется метр здесь и метр квадратный здесь частично сократятся он умножены на амперы то что это вольт вольт делить на метр это как 1 единица напряженности поля все получается теперь здесь у нас 10 минус 8 здесь у нас 10 минус 6 поделив получаем одну сотую 2 и 8 делить на 1 и 4 будет два значит ноль ноль два вольта на метр вот такая напряженность поля в проводнике по которому течет ток 1 ампер это большая напряженность поля когда мы решали задачи на задача по электростатике у нас там были киловольт и на метр пробивное напряжение воздуха 30 киловольт на сантиметр а здесь всего лишь две сотых вольта на метр но ребята не забудьте о том что алюминий это проводник тогда возникает следующий вопрос в электростатике мы говорили что электростатическое поле в проводнике существовать не может а тут мы вычислили его напряженность как же так что же вся электростатика насмарку ребята электростатики изучают свойства неподвижных зарядов в нашей задаче заряды движутся поэтому естественно что электрическое поле которая заставляет их двигаться может существовать то есть если только нет тогда конечно их электрического поля в проводнике быть не может но если есть электрический ток то электрическое поле в проводниках существовать не может так что электростатика наука правильная но не всеобъемлющая но теперь давайте для чего я попросил вас открыть тетради по теории давайте вот эту формулу немножечко с вами обработаем и обсудим и запишем маленький заголовок закон ома в дифференциальной форме закон ома в дифференциальной форме закон ома в дифференциальной форме и так пусть у нас имеется проводник в котором течет ток сила тока и площадь поперечного сечения проводника с удельное сопротивление материала но только что мы с вами решили задачу которая устанавливает связь между напряженностью поля в проводнике силой тока в нем площадью поперечного сечения и удельным сопротивлением эту формулу давайте воспроизведем еще раз я равняются ро и велит на с как не получить вы только что видели мы это сделали вместе теперь смотрите какой физический смысл имеет вот это отношение силы тока к площади поперечного сечения проводника в котором она протекает это сила тока приходящаяся на каждый на каждую единицу поперечного сечения площади поперечного сечения эта величина называется плотностью тока отношение силы тока к площади поперечного сечения проводника в котором он протекает обозначается буквой j и называется плотность тока плотность тока в каких единицах измеряется плотность тока смотрите на формулу ампер на метр квадратный ампер на метр квадратный давайте запишем определение плотностью тока называется физическая величина равная плотностью тока называется физическая величина равная отношению силы тока в проводнике к площади его поперечного сечения равна отношению силы тока в проводнике к площади его поперечного сечения отношению силы тока в проводнике к площади его поперечного сечения а теперь давайте используем эту физическую величину вот в этой формуле тогда у нас получится е равняется х умножить на плотность тока я характеристика электрического поля поле эта причина которая вызывает протекании электрического тока j плотность тока характеризует следствие протекание тока через проводник давайте выразим следствие через причину так как мы это уже делали когда записывали закон ома отсюда мы можем записать что плотность тока равняется единица делить на 1 умножить на е скажите пожалуйста е это вектор или скаляр это вектор так почему бы нам эту формулу не записать более широком смысле а именно плотность тока это векторная величина и тогда можно вот так записать или если мы хотим записать его более компактно без дробная черты вспомним что единица на роя то что это удельная проводимость сигма единица велит народ это удельная проводимость и тогда получится плотность тока равняется сигма на е вот так то что мы с вами записали называется закон ома в дифференциальной форме закон ома в дифференциальной форме давайте теперь словами его сформулирую обратите внимание что здесь ничего не говорится о том какую форму имеет право гек эта плотность тока в данной точке вещества проводящего а это напряженность поля в этой точке поскольку эти величины относятся к некой точки в проводнике то закон и называется закон ома в дифференциальной форме то есть он описывает не проводник в целом у которого есть сопротивление а он описывает только перенос в данной точке проводящей среды проводящего вещества и так записываем плотность тока в данной точке проводника плотность тока в данной точке проводника прямо пропорционально плотность тока в данной точке проводника прямо пропорционально напряженности поля напряженности электрического поля в этой точке прямо пропорционально напряженности электрического поля в этой точке прямо пропорционально напряженности электрического поля в этой точке это соотношение работает в любой точке проводника любой формы если например вы хотите описать только перенос в какой-нибудь цилиндрическом проводнике то вы можете воспользоваться законом ома в привычной нам форме а описать процесс только переноса например вот в таком проводнике вот сюда втекает какой-то ток отсюда он вытекает такой вот конический проводник присоединили к источнику тока скажите пожалуйста плотность тока здесь и здесь будет одинаковая нет потому что один и тот же заряд здесь протекать через маленькую площадь а здесь через большую площадь растут плотность тока больше а вещество у нас одно и то же значит напряженность поля здесь и один будет больше чем здесь е2 то есть мы уже можем как-то обсуждать напряженность поля в разных точках проводника это позволяет нам делать закон ома в дифференциальной форме зная закон ома в дифференциальной форме можно приблизиться мы не решим эти задачи но по-крайней мере можем сказать что тут он понадобится решая например вот такую задачу у вас имеется какая-то среда например толще морской воды вот один заряжен вот один металлический электрод вот второй металлический электрод между ними есть какое-то напряжение как найти силу тока который течет отсюда сюда сила тока оказывается помогает закон ома в дифференциальной форме мы сейчас не сможем решить эту задачу но кстати вам ничего не напоминает эта картинка если мы еще тут напишем плюс а тут минус напоминает силовые линии электрического поля значит посмотрите сюда куда направлена электрическое поле туда же направлено и плотность тока значит существует тесная связь между электростатикой и законами постоянного тока в средах наука едино и разное казалось бы лежащие в разных местах курса физики вещи на самом деле пересекаются правда мы не будем вплотную с этим сейчас работать но знайте что это есть в конце концов у нас с вами я надеюсь сложится единая физическая картина мира но не сейчас а года через полтора отдыхать

Как найти сопротивление тока.

Сопротивление тока: формула

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

1. Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
2. Полупроводники (могут проводить электрический ток, но при определенных условиях).
3. Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом) . Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S.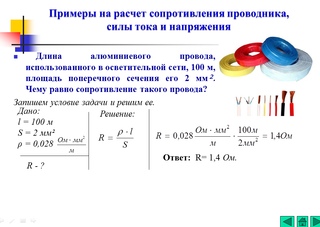 Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться . При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

1. Измеряется частота переменного тока (как правило, 50 Гц).
2. Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

1. Длины проводника.
2. Площади сечения — S.
3. Температуры.
4. Типа материала.
5. Емкости.
6. Индуктивности.
7. Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z . Меняется и закон для полной цепи.

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы , такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника . В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

После несложных мы получаем формулу для вычислений

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь , с его помощью проводим расчёт силы тока через сопротивление и напряжение.

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

При этом согласно тому же закону Ома:

P=I 2 *R

Значит расчёт проводим по формуле:

I 2 =P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R) 1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним .

Его формула выглядит так:

Q=I 2 Rt

Тогда расчет проводите так:

I 2 =QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt) 1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

В своей работе электрик часто сталкивается с вычислением различных величин и преобразований. Так для корректного подбора кабеля приходится подбирать нужное сечение. Логика выбора сечения основана на зависимости сопротивления от длины линии и площади сечения проводника. В этой статье мы рассмотрим, как выполняется расчет сопротивления провода по его геометрическим размерам.

Формула для расчета

Любые вычисления начинаются с формулы. Основной формулой для расчета сопротивления проводника является:

R=(ρ*l)/S

Где R – сопротивление в Омах, ρ – удельное сопротивление, l – длина в м, S – площадь поперечного сечения провода в мм 2 .

Эта формула подходит для расчета сопротивления провода по сечению и длине. Из неё следует, что в зависимости от длины изменяется сопротивление, чем длиннее – тем больше. И от площади сечения – наоборот, чем толще провод (большое сечение), тем меньше сопротивление. Однако непонятной остаётся величина, обозначенная буквой ρ (Ро).

Удельное сопротивление

Удельное сопротивление – это табличная величина, для каждого металла она своя. Она нужна для расчета и зависит от кристаллической решетки металла и структуры атомов.

Из таблицы видно, что самое меньшее сопротивление у серебра, для медного кабеля оно равняется 0,017 Ом*мм 2 /м. Такая размерность говорит нам, сколько приходится Ом при сечении в 1 миллиметр квадратный и длине в 1 метр.

Кстати, серебряное покрытие используется в контактах коммутационных аппаратов, автоматических выключателей, реле и прочего. Это снижает , повышает срок службы и уменьшает . При этом в контактах измерительной и точной аппаратуры используют позолоченные контакты из-за того, что они слабо окисляются или вообще не окисляются.

У алюминия, который часто использовался в электропроводке раньше, сопротивление в 1,8 раза больше чем у меди, равняется 2,82*10 -8 Ом*мм 2 /м. Чем больше сопротивление проводника, тем сильнее он греется. Поэтому при одинаковом сечении алюминиевый кабель может передать меньший ток, чем медный, это и стало основной причиной почему все современные электрики используют . У нихрома, который используется в нагревательных приборах оно в 100 раз больше чем у меди 1,1*10 -6 Ом*мм 2 /м.

Расчет по диаметру

На практике часто бывает так, что площадь поперечного сечения жилы не известна. Без этого значения ничего рассчитать не получится. Чтобы узнать её, нужно измерить диаметр. Если жила тонка, можно взять гвоздь или любой другой стержень, намотать на него 10 витков провода, обычной линейкой измерить длину получившейся спирали и разделить на 10, так вы узнаете диаметр.

Ну, или просто замерить штангенциркулем. Расчет сечения выполняется по формуле:

Обязательны ли расчеты?

Как мы уже сказали, сечение провода выбирают исходя из предполагаемого тока и сопротивления металла, из которого изготовлены жилы. Логика выбора заключается в следующем: сечение подбирают таким способом, чтобы сопротивление при заданной длине не приводило к значительным просадкам напряжения. Чтобы не проводить ряд расчетов, для коротких линий (до 10-20 метров) есть достаточно точные таблицы:

В этой таблице указаны типовые значения сечения медных и алюминиевых жил и номинальные токи через них. Для удобства указана мощность нагрузки, которую выдержит эта линия. Обратите внимание на разницу в токах и мощности при напряжении 380В, естественно, что это предполагается трёхфазная электросеть.

Расчет сопротивления провода сводится к использованию пары формул, при этом вы можете скачать готовые калькуляторы из Плэй Маркета для своего смартфона, например, «Electrodroid» или «Мобильный электрик». Эти знания пригодятся для расчетов нагревательных приборов, кабельных линий, предохранителей и даже популярных на сегодняшний день спиралей для электронных сигарет.

Материалы

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения V на проводнике:

Напомним, что в случае однородного проводника напряжение U совпадает с разностью потенциалов (см. (33.6)).

Обозначенная в формуле (34.1) буквой R величина называется электрическим сопротивлением проводника. Единицей сопротивления служит равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой 1 А.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

где l — длина проводника, S — площадь его поперечного сечения, — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если то R численно равно . В СИ измеряется в ом-метрах (Ом-м).

Найдем связь между векторами j и Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е.

Поэтому на правления векторов j и Е совпадают Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам j и Е (рис. 34.1). Через поперечное сечение цилиндра течет ток силой . Напряжение, приложенное к цилиндру, равно , где Е — напряженность поля в данном месте. Наконец, сопротивление цилиндра, согласно формуле (34.2), равно . Подставив эти значения в формулу (34.1), придем к соотношению

Воспользовавшись тем, что векторы j и Е имеют одинаковое направление, можно написать

Эта формула выражает закон Ома в дифференциальной форме.

Фигурирующая в (34.3) обратная величина называется удельной электрической проводимостью материала. Единица, обратная ому, называется сименсом (См). Соответственно единицей о является сименс на метр (См/м).

Допустим для простоты, что в проводнике имеются носители лишь одного знака. Согласно формуле (31.5) плотность тока в этом случае равна

Сравнение этого выражения с формулой (34.3) приводит к выводу, что скорость упорядоченного движения носителей тока пропорциональна напряженности поля Е, т. е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.

Способность вещества проводить электрический ток характеризуется его удельным сопротивлением либо удельной проводимостью .

Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится.

Для большинства металлов при температурах, близких к комнатной, изменяется пропорционально абсолютной температуре Т:

При низких температурах наблюдаются отступления от этой закономерности (рис. 34.2). В большинстве случаев зависимость от Т следует кривой. Величина остаточного сопротивления рост в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига рост заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле

У большой группы металлов и сплавов при температуре порядка нескольких кельвинов сопротивление скачков обращается в нуль (кривая 2 на рис. 34.2). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг-Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Т при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля разрушающего сверхпроводимость, равна нулю при и растет с понижением температуры.

Полное теоретическое объяснение сверхпроводимости было дано академиком Н. Н. Боголюбовым и независимо от него Дж. Бардином, Л. Купером и Дж. Шриффером (см. § 56 тома 3).

Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволочку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с погрешностью порядка несколько сотых градуса как низкие, так и высокие температуры. В последнее время все большее применение находят термометры сопротивления из полупроводников.

Мы начинаем публикацию материалов новой рубрики “” и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 😉 Кроме того, мы не обойдем стороной закон, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.

Итак, давайте начнем с понятия напряжения .

Напряжение.

По определению напряжение – это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля – это скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:

В пространстве действует постоянное электрическое поле, напряженность которого равна E . Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:

В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:

И в итоге получаем формулу, связывающую напряжение и напряженность:

В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи – это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, “напряжение в резисторе” – не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и “землей” . Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию “земля” 🙂 Так вот “землей” в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).

Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения . Единицей измерения является Вольт (В) . Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт , необходимо совершить работу, равную 1 Джоулю . С этим вроде бы все понятно и можно двигаться дальше 😉

А на очереди у нас еще одно понятие, а именно ток .

Ток, сила тока в цепи.

Что же такое электрический ток ?

Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны…Рассмотрим проводник, к которому приложено определенное напряжение :

Из направления напряженности электрического поля (E ) мы можем сделать вывод о том, что title=»Rendered by QuickLaTeX.com»> (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:

Где e – это заряд электрона.

И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток 🙂

Ток – это упорядоченное движение заряженных частиц под воздействием электрического поля.

Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.

Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E . И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂

Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I ) – это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер . Сила тока в проводнике равна 1 Амперу , если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон .

Мы уже рассмотрели понятия силы тока и напряжения , теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника .

Сопротивление проводника/цепи.

Термин “сопротивление ” уже говорит сам за себя 😉

Итак, сопротивление – физическая величина, характеризующая свойства проводника препятствовать (сопротивляться ) прохождению электрического тока.

Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S :

Сопротивление проводника зависит от нескольких факторов:

Удельное сопротивление – это табличная величина.

Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:

Для нашего случая будет равно 0,0175 (Ом * кв. мм / м) – удельное сопротивление меди. Пусть длина проводника составляет 0.5 м , а площадь поперечного сечения равна 0.2 кв. мм . Тогда:

Как вы уже поняли из примера, единицей измерения сопротивления является Ом 😉

С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи .

И тут на помощь нам приходит основополагающий закон всей электроники – закон Ома:

Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.

Рассмотрим простейшую электрическую цепь:

Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:

Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:

Как видите, все несложно 🙂

Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч! 🙂

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Сопротивление 1 метра медного провода сечением 0.5. Сопротивление провода

Электрическое сопротивление — физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику . Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.

Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.

Удельное сопротивление

Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м. Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле

где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.

Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)

Вещество	p , Ом*мм 2 /2	α,10 -3 1/K
Алюминий	0.0271
Вольфрам	0.055
Железо	0.098
Золото	0.023
Латунь	0.025-0.06
Манганин	0.42-0.48	0,002-0,05
Медь	0.0175
Никель
Константан	0.44-0.52	0.02
Нихром		0.15
Серебро	0.016
Цинк	0.059

Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.

Зависимость удельного сопротивления от деформаций

При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.

При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.

Влияние температуры на удельное сопротивление

Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле

где r это удельное сопротивление после нагрева, r 0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t 2 – температура до нагрева, t 1 — температура после нагрева.

Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.

Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.

На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор . Резистор применяется практически в любой электрической схеме.

Когда производится расчет сечения кабеля, то в частном домостроении или в квартирах для определения этой величины используются два показателя: потребляемая мощность сети и сила тока, проходящая по разводке. Сопротивление в данном случае роли не играет. Все дело в небольшой длине проводов. А вот если длина линии электропередач достаточно большая, то без определения данного показателя здесь не обойтись. К примеру, на начале участка напряжение будет 220-2240 вольт, а на конце уже заниженное 200-220 вольт. А так как все чаще в проводке используются медные кабели и провода, то наша задача в этой статье рассмотреть сопротивление медного провода (таблица сопротивления проводов будет ниже приложена).

Что нам дает сопротивление в общем? В принципе, с его помощью можно узнать параметры используемого провода или материал, из которого он изготовлен. К примеру, если для прокладки линии электропередачи использовался скрытый способ, то зная сопротивление линии, можно точно сказать, какой она длины. Ведь часто прокладка производится под землей и непрямолинейным способом. Или еще один вариант, зная длину участка и его сопротивление можно подсчитать диаметр используемого кабеля, а через него и его сечение. Плюс, зная данную величину, можно узнать материал, из которого этот провод был изготовлен. Это все говорит о том, что не стоит сбрасывать со счетов данный показатель.

Все это касалось электрической проводки, но когда дело касается электроники, то в этой области без определения сопротивления и сопоставления его с другими параметрами не обойтись. В некоторых случаях данный параметр может сыграть решающую роль, даже неправильный подбор провода по сопротивлению может привести к тому, что подключаемый к такому проводнику прибор просто не будет работать. К примеру, если к блоку питания обычного компьютера подключить очень тонкий провод. Напряжение в таком проводнике станет низким, не намного, но этого будет хватать, чтобы компьютер работал некорректно.

От чего зависит сопротивление

Так как мы говорим о медном проводе, то первое от чего зависит этот физический параметр, это медь, то есть, сырьевой материал. Второе – это размеры проводника, а, точнее, его диаметр или сечение (обе величины связаны между собой формулой).

Конечно, есть дополнительные физические величины, которые влияют на сопротивление проводника. К примеру, температура окружающей среды. Ведь известно, что при повышении температуры самого провода, его сопротивление увеличивается. А так как этот показатель находится в обратной зависимости от силы (плотность) тока, соответственно ток при повышении сопротивления, наоборот, снижается. Правда, это относится к тем металлам, которые являются обладателями положительного температурного коэффициента. Для примера можно привести сплав вольфрама, который используется для нити накала лампочки. Такому материалу изменения силы (плотность) тока не страшны при высоком нагреве, потому что этот металл обладает отрицательным температурным коэффициентом.

Расчет сопротивления

Сегодня все сделано для человека. И даже такой простой расчет можно сделать несколькими способами. Есть простые, есть сложные. Начнем с простых.

Первый вариант табличный. В чем его простота? К примеру, таблица на нижнем рисунке.

Здесь все четко показано и взаимосвязано. Зная определенные размеры медного провода, можно определить его сопротивление и силу тока, которую провод может выдержать. Или, наоборот, имея в наличие показатели сопротивления или силы (плотность) тока, которые, кстати, можно определить мультиметром, можно легко определить сечение или диаметр проводника. Данный вариант самый удобный, таблицы можно найти в свободном доступе в интернете.

Второй способ определения – с помощью калькулятора (онлайн). Таких интернетовских приспособлений великое множество, работать с ними удобно и легко. Можно в такой калькулятор вставлять физические величины медного проводника и получать размерные показатели, или, наоборот. Правда, основная масса таких калькуляторов в своей программе имеет одно стандартное значение – это удельное сопротивление меди, равное 0,0172 Ом·мм²/м.

И самый сложный вариант расчета – это провести его своими руками, используя формулу. Вот она: R=pl/S, где:

• р – это то самое удельное сопротивление меди;
• l – длина медного провода;
• S – его сечение.

Хотелось бы отметить, что медь обладает одним из самых низких удельных сопротивлений. Ниже него только серебро – 0,016.

Определить сечение проводника можно через формулу, где основным параметром является его диаметр. А вот определить диаметр можно разными способами, кстати, такая статья на нашем сайте есть, можете прочитать и получить полную и достоверную информацию.

Заключение о теме

Подводим итог всему вышесказанному. Конечно, никто не будет учитывать сопротивление электрической разводки медным кабелем в доме или квартире. Но если дело касается прокладки воздушных или подземных линий электропередач, к примеру, от подстанции до дачного участка, то данный показатель придется учитывать обязательно. Ведь именно он повлияет на качество напряжения в сети дома. А вот рассчитать параметры укладываемых кабелей можно будет разными способами, где показатель сопротивления медного провода (таблица приложена) является одним из основных.

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

1. Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
2. Полупроводники (могут проводить электрический ток, но при определенных условиях).
3. Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом) . Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться . При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

1. Измеряется частота переменного тока (как правило, 50 Гц).
2. Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

1. Длины проводника.
2. Площади сечения — S.
3. Температуры.
4. Типа материала.
5. Емкости.
6. Индуктивности.
7. Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z . Меняется и закон для полной цепи.

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы , такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника . В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

Содержание:

При проектировании электрических сетей в квартирах или частных домах в обязательном порядке выполняется расчет сечения проводов и кабелей. Для проведения вычислений используются такие показатели, как значение потребляемой мощности и сила тока, которая будет проходить по сети. Сопротивление не принимается в расчет из-за малой протяженности кабельных линий. Однако этот показатель необходим при большой длине ЛЭП и перепадах напряжения на различных участках. Особое значение имеет сопротивление медного провода. Такие провода все чаще используются в современных сетях, поэтому их физические свойства должны обязательно учитываться при проектировании.

Понятия и значение сопротивления

Электрическое сопротивление материалов широко используется и учитывается в электротехнике. Данная величина позволяет установить основные параметры проводов и кабелей, особенно при скрытом способе их прокладки. В первую очередь устанавливается точная длина проложенной линии и материал, использованный для производства провода. Вычислив первоначальные данные, вполне возможно измеряемого кабеля.

По сравнению с обычной электрической проводкой, в электронике параметрам сопротивления придается решающее значение. Оно рассматривается и сопоставляется в совокупности с другими показателями, присутствующими в электронных схемах. В этих случаях неправильно подобранное сопротивление провода, может вызвать сбой в работе всех элементов системы. Такое может произойти, если для подключения к блоку питания компьютера воспользоваться слишком тонким проводом. Произойдет незначительное снижение напряжения в проводнике, что вызовет некорректную работу компьютера.

Сопротивление в медном проводе зависит от многих факторов, и в первую очередь от физических свойств самого материала. Кроме того, учитывается диаметр или сечение проводника, определяемые по формуле или специальной таблице.

Таблица

На сопротивление медного проводника оказывают влияние несколько дополнительных физических величин. Прежде всего должна учитываться температура окружающей среды. Всем известно, что при повышении температуры проводника, наблюдается рост его сопротивления. Одновременно с этим происходит снижение силы тока из-за обратно пропорциональной зависимости обеих величин. В первую очередь это касается металлов с положительным температурным коэффициентом. Примером отрицательного коэффициента является вольфрамовый сплав, применяющийся в лампах накаливания. В этом сплаве сила тока не снижается даже при очень высоком нагреве.

Как рассчитать сопротивление

Для расчетов сопротивления медного провода существует несколько способов. К наиболее простым относится табличный вариант, где указаны взаимосвязанные параметры. Поэтому, кроме сопротивления, определяется сила тока, диаметр или сечение провода.

Во втором случае используются разнообразные . В каждый из них вставляется набор физических величин медного провода, с помощью которых получаются точные результаты. В большинстве подобных калькуляторов используется в размере 0,0172 Ом*мм 2 /м. В некоторых случаях такое усредненное значение может повлиять на точность вычислений.

Наиболее сложным вариантом считаются ручные вычисления, с использованием формулы: R = p x L/S, в которой р — удельное сопротивление меди, L — длина проводника и S — сечение этого проводника. Следует отметить, что сопротивление медного провода таблица определяет, как одно из наиболее низких. Более низким значением обладает лишь серебро.

Понятие об электрическом сопротивлении и проводимости

Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Электронная теория так объясняет сущность электрического сопротивления металлических проводников. Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.

Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении.

Сопротивление обозначается латинскими буквами R или r .

За единицу электрического сопротивления принят ом.

Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм2 при температуре 0° С.

Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4ом.

Для измерения сопротивлений большой величины принята единица, называемая мегомом.

Один мегом равен одному миллиону ом.

Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник.

Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.

Электрической проводимостью называется способность материала пропускать через себя электрический ток.

Так как проводимость есть величина, обратная сопротивлению, то и выражается она как 1/R ,обозначается проводимость латинской буквой g.

Влияние материала проводника, его размеров и окружающей температуры на величину электрического сопротивления

Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.

Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавита р. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.

Например, удельное сопротивление меди равно 0,017, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,017 ом. Удельное сопротивление алюминия равно 0,03, удельное сопротивление железа — 0,12, удельное сопротивление константана — 0,48, удельное сопротивление нихрома — 1-1,1.

Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.

Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.

Чтобы лучше понять эту зависимость, представьте себе две пары сообщающихся сосудов, причем у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая. Ясно, что при заполнении водой одного из сосудов (каждой пары) переход ее в другой сосуд по толстой трубке произойдет гораздо быстрее, чем по тонкой, т. е. толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т. е. первый оказывает ему меньшее сопротивление, чем второй.

Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь площадь поперечного сечения проводника :

R = p l / S ,

Где — R — сопротивление проводника, ом, l — длина в проводника в м, S — площадь поперечного сечения проводника, мм 2 .

Площадь поперечного сечения круглого проводника вычисляется по формуле:

S = Пи х d 2 / 4

Где Пи — постоянная величина, равная 3,14; d — диаметр проводника.

А так определяется длина проводника:

l = S R / p ,

Эта формула дает возможность определить длину проводника, его сечение и удельное сопротивление, если известны остальные величины, входящие в формулу.

Если же необходимо определить площадь поперечного сечения проводника, то формулу приводят к следующему виду:

S = p l / R

Преобразуя ту же формулу и решив равенство относительно р, найдем удельное сопротивление проводника:

р = R S / l

Последней формулой приходится пользоваться в тех случаях, когда известны сопротивление и размеры проводника, а его материал неизвестен и к тому же трудно определим по внешнему виду. Для этого надо определить удельное сопротивление проводника и, пользуясь таблицей, найти материал, обладающий таким удельным сопротивлением.

Еще одной причиной, влияющей на сопротивление проводников, является температура .

Установлено, что с повышением температуры сопротивление металлических проводников возрастает, а с понижением уменьшается. Это увеличение или уменьшение сопротивления для проводников из чистых металлов почти одинаково и в среднем равно 0,4% на 1°C . Сопротивление жидких проводников и угля с увеличением температуры уменьшается.

Электронная теория строения вещества дает следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При нагревании проводник получает тепловую энергию, которая неизбежно передается всем атомам вещества, в результате чего возрастает интенсивность их движения. Возросшее движение атомов создает большее сопротивление направленному движению свободных электронов, отчего и возрастает сопротивление проводника. С понижением же температуры создаются лучшие условия для направленного движения электронов, и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов .

Сверхпроводимость , т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре — 273° C , называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.

Пример определения индуктивного сопротивления ВЛ 10 кВ

В данной статье будет рассматриваться пример определения индуктивного сопротивления воздушной линии 10 кВ.

Пример

Требуется определить индуктивное сопротивление воздушной линии 10 кВ со сталеалюминиевыми проводами марки АС-50/8,0, длина линии составляет 5 км, используется промежуточная опора П10-16.

Рис.1 — Габаритный чертеж опоры П10-16

Решение

Определять индуктивное сопротивление проводов будем по формулам представленным в статье: «Определение активных и индуктивных сопротивлений проводов».

1. Определяем среднее геометрическое расстояние между проводами по формуле [Л1. с19], зная расстояния между фазами по габаритному чертежу на опору П10-16 (см. рис.1):

где:

• D_А-В = 1080 мм — расстояние между проводами фаз А и В;
• D_В-С = 1080 мм — расстояние между проводами фаз В и С;
• D_С-А = 1110 мм — расстояние между проводами фаз С и А.

2. Определяем индуктивное сопротивление для проводов марки АС-50/8,0 по формуле [Л1.с.19]:

где:

• Dср. = 1090 мм – среднее геометрическое расстояние между проводами;
• dр = 9,6 мм – расчетный диаметр провода, определяется по ГОСТ 839-80, таблица 4;

С не большой погрешностью, такой же результат можно получить по приложению П30 [Л1.с. 84], если кривую для провода сечением 50 мм2 продлить до Dср = 1,09 м, то индуктивное сопротивление будет равно 0,358 Ом/км. Принимаю х_инд. = 0,356 Ом/км, так как считаю это более точное значение.

3. Определяем индуктивное сопротивление для всей линии:

где: L = 5 км – длина воздушной линии 10 кВ.

Для упрощения расчетов индуктивного сопротивления проводов рекомендую использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.

Литература:

1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.

Всего наилучшего! До новых встреч на сайте Raschet.info.

Поделиться в социальных сетях

По какой формуле рассчитывается сопротивление провода? — MVOrganizing

По какой формуле рассчитывается сопротивление провода?

Удельное сопротивление («ρ») — это свойство любого проводящего материала, показатель, используемый для определения сквозного сопротивления проводника данной длины и площади в этой формуле: R = ρl / A. Удельное сопротивление для материалов указывается в единицах Ом-см / фут или Ом-метр (метрическая система).

Каково сопротивление медного провода длиной 200 футов?

Расчетное значение сопротивления данного медного провода равно 5.17 Ом.

Есть ли у медного провода сопротивление?

Медь имеет более низкое удельное сопротивление и лучше проводит электричество, чем железо. Медь — лучший проводник, чем железо, а это значит, что ток может проходить легче (с меньшим сопротивлением) через медь.

Какое значение удельного сопротивления медного проводника?

Удельное сопротивление меди, которая является хорошим проводником, составляет 1,72 × 10-8 Ом · м.

Как найти сопротивление?

Если вам известен полный ток и напряжение во всей цепи, вы можете найти полное сопротивление, используя закон Ома: R = V / I.Например, параллельная цепь имеет напряжение 9 вольт и общий ток 3 ампера. Общее сопротивление RT = 9 вольт / 3 ампера = 3 Ом.

Как рассчитать сопротивление параллельно?

4. «Вы можете найти ОБЩЕЕ СОПРОТИВЛЕНИЕ в параллельной цепи по следующей формуле: 1 / Rt = 1 / R1 + 1 / R2 + 1 / R3 +». Прежде чем мы приступим к вычислениям, вспомните, что мы сказали в начале в этом разделе: «Общее сопротивление параллельной цепи НЕ равно сумме резисторов (как в последовательной цепи).

Почему в параллельной цепи общее сопротивление меньше?

В параллельной цепи сопротивление сети уменьшается по мере добавления дополнительных компонентов, потому что есть больше путей для прохождения тока. Два резистора имеют одинаковую разность потенциалов. Полный ток в цепи — это сумма токов, протекающих через каждую ветвь.

Что называется эквивалентным сопротивлением?

Эквивалентное сопротивление — это суммарное сопротивление, подключенное параллельно или последовательно.По сути, схема может быть последовательной или параллельной. Электрическое сопротивление показывает, сколько энергии нужно, когда вы пропускаете заряды / ток через свои устройства.

Что происходит с эффективным сопротивлением при параллельном подключении двух или более резисторов?

При параллельном подключении резисторов от источника протекает больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже. Каждый резистор, включенный параллельно, имеет такое же полное напряжение источника, как на него, но делит общий ток между ними.

Какое эффективное сопротивление последовательно и параллельно?

Эффективное сопротивление в последовательной комбинации двух равных сопротивлений равно ‘s’. Когда они соединены параллельно, общее сопротивление составляет p. Если s = np, то минимально возможное значение ′ n ′ равно.

Вычислитель сопротивления провода

Формула сопротивления проволоки

сопротивление = удельное сопротивление * длина / площадь поперечного сечения
R = ρ * L / A

Объясните сопротивление провода и факторы, влияющие на его свойства?

Провод сопротивления — это провод, предназначенный для изготовления электрических резисторов (которые используются для контроля количества тока в цепи).Лучше, если используемый сплав будет иметь высокое удельное сопротивление, поскольку тогда можно использовать более короткую проволоку. Во многих ситуациях стабильность резистора имеет первостепенное значение, и поэтому температурный коэффициент сопротивления сплава и коррозионная стойкость играют большую роль при выборе материала. Когда резистивная проволока используется для нагревательных элементов (в электрических нагревателях, тостерах и т. Д.), Большое значение имеют высокое удельное сопротивление и стойкость к окислению. Иногда резистивный провод изолирован керамическим порошком и заключен в трубку из другого сплава.Такие нагревательные элементы используются в электрических духовках и водонагревателях, а также в специализированных формах для варочных панелей.

Как рассчитать сопротивление провода?

В калькуляторе сопротивления провода для расчета сопротивления используется сопротивление = удельное сопротивление * длина / площадь поперечного сечения . Сопротивление провода является мерой сопротивления току в электрической цепи.Сопротивление измеряется в омах и обозначается греческой буквой омега (Ом). Сопротивление и обозначается символом R .

Как рассчитать сопротивление провода с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для определения сопротивления провода, введите удельное сопротивление (ρ) , длину (L) и площадь поперечного сечения (A) и нажмите кнопку «Рассчитать». Вот как можно объяснить расчет сопротивления провода с заданными входными значениями -> 5.100E-6 = 1,7E-05 * 3/10 .

Найдите сопротивление 1000 м медного провода 25 кв. М. Cdot, класс 11, физика CBSE

Подсказка: В этом вопросе используйте понятие удельного сопротивления, то есть это свойство материала, оно не зависит от сопротивления, длины и площадь поперечного сечения провода. Это зависит от материала, то есть будет постоянным для медной проволоки.

Полный пошаговый ответ:
В вопросе указано, что медный провод имеет длину \ [1000 \; {\ text {метров}} \], а площадь поперечного сечения равна \ [25 \ ; {\ text {sq}} {\ text {mm}} \].Нам также известно, что сопротивление медного провода составляет \ [1/5 {\ text {8}} \; {\ text {ohm}} \] на метр длины, а площадь поперечного сечения равна \ [{\ text {1}} \; {\ text {sq}} {\ text {mm}} \].
Для расчета сопротивления медного провода мы используем формулу удельного сопротивления:
\ [\ rho = R \ dfrac {A} {l} \]
Здесь \ [\ rho \] — удельное сопротивление материала в Ом. метр, а \ [l \] — длина медного провода, а \ [A \] — площадь поперечного сечения медного провода.
Подставляем значения удельного сопротивления меди, если сопротивление медного провода составляет \ [1/5 {\ text {8}} \; {\ text {ohm}} \] на метр или 1000 долларов США \; {\ text {мм}} $ длина, а площадь поперечного сечения равна \ [{\ text {1}} \; {\ text {sq}} {\ text {mm}} \].
\ [\ Rightarrow \ rho = \ left ({\ dfrac {1} {{58}}} \ right) \ dfrac {{\ left (1 \ right)}} {{\ left ({1000} \ right) }} \]
После упрощения получаем,
$ \ Rightarrow \ rho = \ dfrac {1} {{58000}} \; \ Omega \ cdot {\ text {mm}} $
Теперь мы вычисляем сопротивление для медный провод имеет длину \ [1000 \; {\ text {метров}} \], а площадь поперечного сечения составляет \ [25 \; {\ text {sq}} {\ text {мм}} \].
Для расчета сопротивления медного провода мы используем формулу удельного сопротивления:
\ [\ rho = R \ dfrac {A} {l} \]
Теперь изменим приведенную выше формулу
$ \ Rightarrow R = \ dfrac {{ \ rho l}} {A} $
Подставьте значения в приведенное выше уравнение
\ [R = \ left ({\ dfrac {1} {{58000}}}} \ right) \ left ({\ dfrac {{1000 \ раз {{10} ^ 3}}} {{25}}} \ right) \]
После упрощения получаем,
\ [\ поэтому R = \ dfrac {{20}} {{29}} \; \ Omega \]

Следовательно, сопротивление медного провода равно \ [\ dfrac {{20}} {{29}} \ Omega \], а длина провода составляет \ [1000 \; {\ text {метров}} \ ] и \ [2 {\ text {5}} \; {\ text {sq}} {\ text {mm}} \] — это поперечное сечение.

Примечание: Из приведенного выше расчета можно сделать вывод, что сопротивление провода зависит от длины и площади поперечного сечения провода, то есть сопротивление прямо пропорционально длине и обратно пропорционально площади сечение провода.

Сопротивление провода — Электроника — Таблицы Basic

Сопротивление провода определяется материалом, длиной и поперечным сечением провода. Вы можете рассчитать сопротивление провода с помощью калькулятора ниже или рассчитать его самостоятельно по формулам.

Формулы

R является обозначением сопротивления и измеряется в омах (Ом).
A является обозначением площади и измеряется в квадратных метрах (м ² ).
ρ является символом удельного сопротивления и измеряется в ом-метре (Ом⋅м).
l — это обозначение длины, которое измеряется в метрах (м).

Калькулятор

Введите три значения, чтобы рассчитать оставшееся.

9012 мм диаметр

материал	удельное сопротивление ρ 10⁻⁹Ом⋅м
серебро	15.9
медь	16,8
алюминий	26,5
вольфрам	56
железо	97 пл.1
свинец	220
ртуть	980
нихром	1000
константан	49130 AW0
					901 9013 9013 901 9013 9013 901 901 901 901 901 901 30101 901 301 9013 901 9013 901 9013 901 901 901 901 901 901 901 901 901 301 901 901 901 301 901 301 901 301 901 301 901 901 901 9013 0,51 901 901 9013 0,01 9013 0,01 9013 0,013 площадь (тыс. Мил) площадь (мм 2 ) 0000 (4/0) 0.46 11,684 211,6 107,219 000 (3/0) 0,40964 10,4049 167.806 85,0281 0 001 85,0281 133.077 67.4309 0 (1/0) 0.32486 8.25146 105.534 53.4751 1 0.2893 7,34814 83,6927 42,4077 2 0,25763 6,54371 66,3713 33,6308 3 0,22942 5,82734 52,6348 26,6705 4 0,20431 5,1894 41,7413 21,1506 5 0,18194 4.62129 +33,1024 16,7732 6 0,16202 4,11538 26,2514 13,3018 7 0,14429 3,66485 20,8183 10,5488 8 0,12849 3,26364 16,5097 8,36556 9 0,11442 2, 13.0928 6,63419 10 0,1019 2,58819 10,383 5,26115 11 11 0,09074 2,301 0301 9013 8,2301 6,52995 3,30877 13 0,07196 1,82783 5,17848 2.62398 14 0,06408 1,62773 4,10672 2,08091 15 0,05707 1,44953 3,25678 1,65023 16 0,05082 1,29085 2,58274 1,3087 17 0,04526 1,14953 2,04821 1,03784 18 0.0403 1,02369 1,6243 0,82305 19 0,03589 0, 1,28813 0,65271 0,02846 0,72295 0,81011 0,41049 22 0,02535 0.6438 0,64245 0,32553 23 0,02257 0,57332 0,50949 0,25816 24 0,01 0,45467 0,32042 0,16236 26 0,01594 0,40489 0.2541 0,12876 27 0,0142 0,36057 0.20151 0,10211 28 0,012641 0,32109 0,12673 0,06422 30 0,01003 0,25464 0,1005 0.+05093 31 0,00893 0,22676 0,0797 0,04039 32 0,00795 0,20194 0,06321 0,03203 33 0,00708 0,17983 0,05013 0,0254 34 0,0063 0,16014 0,03975 0,02014 35 0.00561 0,14261 0,03152 0,01597 36 0,005 0,127 0,025 0,01267 5 37430 0,01267 5 0,00 0,00397 0,10072 0,01572 0,00797 39 0,00353 0.08969 0,01247 0,00632 40 0,00314 0,07987 0,00989 0,00501 Провод резистора Резисторы и провод резистора Резисторы используются для ограничения силы тока, протекающего по цепи. В электрических цепях они также используются для разделения напряжения и рассеивания мощности.Резисторы в электронных устройствах обычно изготавливаются из углерода, углеродной пленки, металлической пленки и оксида металла. Резисторы с проволочной обмоткой используют металлическую проволоку, обернутую вокруг материала сердечника, часто керамики, стекловолокна или пластика. При ограничении протекания тока резисторы выделяют тепло. В электронном оборудовании это считается нежелательным побочным эффектом. Однако, если желаемым результатом является тепло, резисторы являются отличным пассивным источником тепла. Резисторы могут быть фиксированными или переменными по величине доступного сопротивления.Это означает, что количество тепла также можно варьировать. Использование резистивной проволоки позволяет пользователю создавать необходимое количество тепла, используя проволоку из различных материалов и размеров. Типы проводов сопротивления Нихром часто используется для изготовления резисторной проволоки. Нихром — это сплав хрома и никеля, иногда с добавлением железа. Различные материалы и процентное содержание материалов позволяют создавать разное удельное сопротивление.Этот основной сплав устойчив к коррозии и имеет высокую температуру плавления, примерно 1400 ° C (2552 ° F). Устойчивость к высоким температурам делает его отличным выбором для систем отопления. Нихром 60 — это сплав, состоящий из 60% никеля, 16% хрома и 24% железа. Нихром 60 имеет температуру плавления 1350 ° C (2462 ° F) и максимальную рабочую температуру 900 ° C (1652 ° F). Имеется диаграмма для определения удельного сопротивления при определенных температурах. Никель-железные (NiFe) сплавы имеют высокий температурный коэффициент при низком удельном сопротивлении.Провода резисторов из этих сплавов создают нагревательные элементы, которые уменьшают требуемую мощность при повышении температуры. Проволока Kanthal также является отличным выбором в качестве резисторной проволоки в теплоизлучающих устройствах. Kanthal A-1 часто используется для печей. Сплавы Kanthal обеспечивают более стабильную температуру элемента и более жесткие допуски. Проволока легче по сравнению с сплавами NiFe или NiCr. Кроме того, он менее подвержен коррозии. Выбор провода Чтобы выбрать правильный провод резистора для проекта, необходимо учитывать удельное сопротивление провода. Термическая способность, включая температуру плавления, имеет решающее значение. Сплавы нужно выбирать по коррозионной стойкости и весу. В приложениях, требующих точных температур, допуски для проволоки также должны учитываться при принятии решения. Общие расчеты Ток или сила тока протекает через устройство или резистор.Напряжение течет через устройство или резистор. Сопротивление измеряется в Ом. Закон Ома предусматривает простые методы определения напряжения, тока и сопротивления: В = ИК Напряжение (В) = ток (I), умноженное на сопротивление (R) Чтобы найти ток, Закон Ома перестраивается: I = V / R Ток = напряжение, деленное на сопротивление. Чтобы найти сопротивление: R = V / I Сопротивление = напряжение, деленное на ток. Например, если вы измеряете напряжение 12 вольт при токе 40 миллиампер, сопротивление будет 300 Ом. Формула, используемая для определения физического сопротивления провода: Сопротивление = rL / A . Чтобы определить величину сопротивления, обеспечиваемого куском проволоки, вам необходимо знать три фактора. 1) Длина провода, обозначенная символом L . 2) Площадь поперечного сечения или диаметр провода, обозначенный символом A . 3) Постоянное удельное сопротивление материала проволоки, обозначенное символом r . Это означает, что чем больше диаметр провода, тем меньшее сопротивление он обеспечивает. Мощность или тепловыделение также можно определить по формулам. P = I2R — величина тока в квадрате, умноженная на сопротивление. P = IV — величина тока, умноженная на напряжение. P = V2 / R — квадрат напряжения, деленный на сопротивление. Дополнительные полезные формулы Количество мощности или тепловой энергии, выделяемой с течением времени, определяется интегралом мощности с течением времени. P = f t2 / t1 v (t) I (t) dt Удельное сопротивление при 20 ° C (68 ° F) Вт мм2 / м (Вт / смс) Определение размера и типа провода резистора Вопрос: Если я знаю желаемое напряжение и мощность, как мне рассчитать / узнать, какой размер и тип провода подходит для изготовления резистора или нагревательного элемента? Ответ: Когда вы знаете напряжение системы и мощность или мощность, которую вы хотите достичь, вы можете использовать стандартную формулу мощности, чтобы определить необходимое сопротивление. P = V2 / R Измените эту формулу, чтобы определить сопротивление: R = V2 / P Грубый расчет для создания нагревательного элемента мощностью 1000 Вт на источнике питания 250 В показывает, что вам потребуется сопротивление 62,5 Ом. 250 вольт в квадрате = 62500 вольт. 62500 вольт разделить на 1000 ватт = 62,5 Ом. Для полных расчетов необходимо учитывать длину провода и удельное сопротивление. В приведенной ниже таблице содержится краткий справочник по расчетам типа и калибра провода.Например, чтобы нагреть нихром 32 AWG до 400 ° F, требуется 0,68 А. Мы поможем вам с расчетами по определению типа и толщины провода сопротивления, который вам нужен. Калибр (AWG) Нихром 60 1150 ° C (210 ° F) Kanthal A1 1400 ° C (2550 ° F) 16 * 18 * 20 * 22 * 24 * 26 * 27 * 28 * 29 * 30 * 32 * * 33 * 34 * 36 20.3 Сопротивление и удельное сопротивление — Физика колледжа: OpenStax Задачи и упражнения 1: Каково сопротивление отрезка медного провода 12 калибра длиной 20,0 м и диаметром 2,053 мм? 2: Диаметр медного провода нулевого сечения составляет 8,252 мм. Найдите сопротивление такого провода длиной 1,00 км, используемого для передачи энергии. 3: Если вольфрамовая нить диаметром 0,100 мм в лампочке должна иметь сопротивление [латекс] \ boldsymbol {0.3 \; \ textbf {V}} [/ latex] применяется к нему? (Такой стержень может быть использован, например, для изготовления детекторов ядерных частиц.) 6: (a) До какой температуры вы должны нагреть медный провод, изначально равный 20,0 ° C, чтобы удвоить его сопротивление, не обращая внимания на любые изменения размеров? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах? 7: Резистор из нихромовой проволоки используется в приложениях, где его сопротивление не может измениться более чем на 1,00% от значения 20.0ºC. В каком температурном диапазоне его можно использовать? 8: Из какого материала изготовлен резистор, если его сопротивление на 40,0% больше при 100 ° C, чем при 20,0 ° C? 9: Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0 ° C до 55,0 ° C, содержит резисторы из чистого углерода. В какой степени их сопротивление увеличивается в этом диапазоне? 10: (a) Из какого материала сделана проволока, если она имеет длину 25,0 м, диаметр 0,100 мм и сопротивление [латекс] \ boldsymbol {77.7 \; \ Omega} [/ latex] при 20,0ºC? (б) Каково его сопротивление при 150 ° C? 11: Если принять постоянный температурный коэффициент удельного сопротивления, каков максимальный процент уменьшения сопротивления константановой проволоки, начиная с 20,0 ° C? 12: Проволока протягивается через матрицу, растягивая ее в четыре раза по сравнению с исходной длиной. По какому фактору увеличивается его сопротивляемость? 13: Медный провод имеет сопротивление [латекс] \ boldsymbol {0,500 \; \ Omega} [/ латекс] при 20.{\ circ} \ textbf {C}} [/ latex]), когда он находится при той же температуре, что и пациент. Какова температура пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0 ° C (нормальная температура тела)? (b) Отрицательное значение [latex] \ boldsymbol {\ alpha} [/ latex] не может поддерживаться при очень низких температурах. Обсудите, почему и так ли здесь. (Подсказка: сопротивление не может стать отрицательным.) 15: интегрированные концепции (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити.{\ circ} \ textbf {C}} [/ латекс]. б) На какой процент ваш ответ отличается от приведенного в примере? 16: необоснованные результаты (a) До какой температуры необходимо нагреть резистор из константана, чтобы удвоить его сопротивление, при условии постоянного температурного коэффициента удельного сопротивления? б) разрезать пополам? (c) Что необоснованного в этих результатах? (d) Какие допущения необоснованны или какие посылки несовместимы? Сопротивление и провода — GCSE Science Выдержки из этого документа… Дополнительная наука 21 века Письменный научный эксперимент — Сопротивление и провода Как на сопротивление хромоникелевой проволоки влияет ее длина и диаметр? Как на сопротивление хромоникелевой проволоки влияет ее длина и диаметр? Введение Это исследование определяет, как изменение длины никель-хромовых (нихромовых) проводов при прохождении через них электрического тока влияет на их сопротивление.Он также определяет, как на сопротивление влияет изменение диаметра используемой проволоки. Сопротивление — это «свойство не проводить электрическую или тепловую энергию». Сопротивление — это сила, которая препятствует прохождению электрического тока по цепи, поэтому требуется больше энергии, чтобы толкать заряженные частицы по цепи. Сам контур может противостоять потоку частиц, если провода очень тонкие или очень длинные, например нить накаливания через электрическую лампочку. Сопротивление измеряется в омах. Резистор имеет сопротивление в один Ом, если требуется напряжение в один вольт, чтобы протолкнуть через него ток в один ампер. Джордж Ом обнаружил, что ЭДС (электромагнитная сила) цепи прямо пропорциональна току, протекающему по цепи. Это означает, что если вы утроите одно, вы утроите другое. Он также обнаружил, что цепь иногда сопротивляется потоку электричества. Он называл это сопротивлением. Затем он придумал правило для расчета сопротивления цепи: В ÷ I = R, V = I × R и R = V ÷ I В –Напряжение (вольты) I — ток (амперы) R — сопротивление (Ом) При проведении этого эксперимента я исследовал сопротивление никель-хромовой проволоки.В этом исследовании я исследую 2 переменные, которые влияют на сопротивление провода. Это диаметр проволоки и длина проволоки. 9,4 70 6,42 10,9 80 6,45 12,4 90 6,47 13,9 100 13,9 100 нам, что означает «n», чтобы формула y = nx работала для каждого результата.Это полезно для нас тем, что позволяет нам увидеть в деталях точность наших результатов. Это потому, что результаты кажутся точными пропорциями между их длиной и сопротивлением. Этот расчет говорит нам, что на самом деле это не совсем верно для данного эксперимента. Как показано в таблице, результаты имеют тенденцию к увеличению. Этого не должно быть, если две переменные прямо пропорциональны друг другу. Однако такое увеличение значения «n» можно объяснить. Мое объяснение этого аналогично тому, почему полосы диапазона увеличиваются в размере разброса по мере увеличения длины.Я предполагаю, что это связано с тем, что я проводил тесты в хронологическом порядке от более коротких проводов к более длинным. Из-за того, что я каждый раз использовал один и тот же провод, температура могла незначительно повыситься, несмотря на то, что я на мгновение отключал питание между каждой записью. Этого времени, когда блок питания был выключен, могло быть недостаточно. В испытательном проводе может накапливаться тепло, вызывая увеличение сопротивления, что показано на схемах на стр. 3b в разделе «Введение».Если бы результаты были нарисованы на графике и если бы я ждал, пока провод остынет дольше, результаты были бы более точными, результаты для ‘n’ в уравнении y = nx показали бы точно прямую линию, потому что соотношение Между длиной и сопротивлением прямо и точно пропорционально, как рассчитано ниже. Я вычислил среднее значение «n», используя значения «n» для различной длины. Я вычислил значение среднего, сложив все 10 значений для «n» и разделив эту сумму на количество результатов, которое составило 10.Это дало мне 6.31. Однако это среднее значение не является точным из-за того, что результаты не являются полностью точными, как указано выше. Гораздо более точным способом вычисления значения ‘n’, которое должно работать в уравнении y = nx, было бы использование значения ‘n’ для результата, взятого первым в хронологическом порядке, потому что здесь нет несправедливости в результате. вызвано нагревом, потому что проволока не могла быть нагрета. Это значение составляет 5,88. Очевидно, что это значение не является 100% точным, отчасти из-за того, что при вычислении «n» принималось только 2d.p, но это наиболее точное прочтение «n», которым я могу закончить. Это значение «n» можно использовать для любой длины, поскольку соотношение между длиной (y) и сопротивлением (x) всегда прямо пропорционально. Следовательно, это значение «n» можно использовать для расчета сопротивления провода любой длины. Например, если «n» всегда равно 5,88, тогда y = 5,88 × x. Таким образом, 5,88 × x всегда дает длину провода с таким удельным сопротивлением. А y / 5,88 всегда будет давать значение сопротивления, которое имеет эта длина провода.Это значение «n» относится только к проводам того же диаметра, что и рассчитанный «n» (34 мм). Например, если бы мне нужно было найти значение сопротивления провода длиной 250 см, я бы использовал расчет 250 / 5,88. Это дало бы мне ответ 42,5 Ом. Или, если бы я рассчитал длину провода диаметром 34 мм при сопротивлении 5 Ом, я бы использовал расчет 5,88 × 5. Это даст мне ответ 29,4 см. Можно доказать, что это достаточно точно, если отобразить это на графике.Я сделал это, как показано на графике. Показание, представленное на графике, составляет 31 см, что, учитывая возможную неточность значения «n», очевидно, подтверждает надежность уравнения и точность записанных результатов. Можно рассчитать величину сопротивления 10 см провода, прочитав график, чтобы измерить, насколько сопротивление увеличивается каждые 10 см вдоль провода. Чтобы рассчитать сопротивление, которое имеет 10 см провода, я просто прочитал по графику от средней точки 10 см до оси «y» и обнаружил, что сопротивление равно 1.8 Ом. Затем я сделал то же самое для записи 20 см и нашел измерение для 3,3 Ом. Чтобы рассчитать изменение сопротивления, я вычел 1,8 из 3,3, что показало изменение сопротивления на 1,5 Ом. Таким образом, показано, что это величина сопротивления, которую имеет 10 см провода, потому что разница в сопротивлении между 10 см и 20 см (разница в длине 10 см) составляет 1,5 Ом. Я вычислил сопротивление 15 см провода, прочитав сопротивление в омах при длине провода 25 см.График показывает, как я читал запись. График показывает, что на 25 см сопротивление составляет 4,0 Ом. Если вычесть предыдущую запись для 10 см из 1,8 из 4,0, остается 2,2 Ом. ). Таким образом, 2,2 Ом — это величина сопротивления 15 см провода, потому что разница между 10 см и 25 см составляет 15 см. Этот метод можно использовать для определения величины сопротивления для проволоки любой длины, при условии, что это никель-хромовая проволока диаметром 0,34 мм. Этот метод будет точным только с проводом с этими свойствами, потому что провод, используемый для записи этих данных, действительно имел эти свойства.Любое изменение этих свойств привело бы к разному сопротивлению, и поэтому каждая длина провода имела бы разное сопротивление. Как вкратце упоминалось ранее, эти результаты, в целом, очень точны из-за того, что при планировании получения результатов с очень маленькими параметрами, показанными полосами с узким диапазоном, было уделено особое внимание. Также показана точность, поскольку каждый средний результат почти полностью соответствует «линии наилучшего соответствия» графика. Несмотря на такую ​​точность, показано, что результаты с большей длиной провода имеют более широкий параметр в полосах диапазона.Это указывает на небольшую неточность в записях. Возможная причина этого может заключаться в том, что, несмотря на то, что я выключаю оборудование между каждой записью, провод мог нагреться и сохранить часть тепла от предыдущей записи. Эта теория соответствует модели, потому что полосы диапазона становятся шире по мере увеличения длины провода. Из-за того, что сначала измерялось более короткое количество проволоки, увеличение нагрева со временем могло вызвать постепенное увеличение сопротивления, что привело к увеличению размера линейки диапазона.Это не определенная причина, но вполне вероятная. Если предположить, что эта идея верна, более низкие параметры были бы записаны сначала при более низкой температуре, а более высокие параметры полосок диапазона были бы записаны позже, когда проволока была более горячей. Если бы мне пришлось провести этот эксперимент во второй раз, я бы увеличил время, в течение которого питание было отключено, чтобы обеспечить достаточное количество времени, чтобы позволить проводу полностью остыть. Это будет означать, что каждая полоса диапазона будет более похожего размера и не будет увеличиваться при увеличении длины. Как показано на графике, линия наилучшего соответствия, если она будет прямой, не пройдет через точку (0, 0) на графике. Предполагается, что график может проходить через эту точку; однако это не указано на графике. Это могло быть либо из-за ошибки записи, либо из-за отсутствия деталей в записях. Идея об ошибке записи может быть проверена повторным проведением эксперимента. Гораздо более вероятное объяснение состоит в том, что измерения были недостаточно подробными, чтобы показать небольшую кривую в начале «линии наилучшего соответствия».Предполагая, что результаты находятся в правильном положении, оставшееся объяснение будет заключаться в том, что если бы промежутки между независимыми переменными были меньше, например каждые 1 см результаты могли показать небольшую кривую в тенденции результатов. Это ответит на этот вопрос. Возможно, что, как показано с текущими данными, результаты, несмотря на отсутствие подробностей, не будут иметь кривой в сторону (0, 0), а вместо этого продолжат около (0, 0,004). Это могло быть возможно, потому что в момент, когда длина достигает оси «Y», сопротивление может упасть до 0 Ом.Это, безусловно, так, потому что ни один провод, не имеет сопротивления, однако минимальное количество проволоки может начинаться при определенном сопротивлении, не следуя пропорциональной « линии наилучшего соответствия » от (0, 0) со скоростью увеличения. 2,6 Ом на 10 см. Наличие небольшого количества проволоки может привести к непропорциональной величине начального сопротивления. Заключение В заключение этого эксперимента результаты показывают, что с увеличением длины нихромовой проволоки сопротивление увеличивается.Величину сопротивления, вызванную добавлением определенной длины провода, можно рассчитать путем измерения разницы в сопротивлении между двумя значениями длины с разницей в количестве проволоки, измеряемой на предмет сопротивления. Например, чтобы найти сопротивление 10 см нихромовой проволоки диаметром 34 мм, расчет должен вычесть сопротивление 20 см проволоки из сопротивления 10 см, чтобы получить сопротивление 10 см проволоки. Как показано выше, эта разница в сопротивлении составляет 1,5 Ом.Таким образом, очевидно, что на каждые 10 см добавленного провода того же диаметра добавляется сопротивление 1,5 Ом. Эти результаты подтверждают мой первоначальный прогноз, и поэтому мое предположение о взаимосвязи между сопротивлением и длиной действительно было правильным. Однако есть некоторые ограничения на вывод из-за разброса в барах диапазона. Разброс или размер полос диапазона увеличивается довольно сильно по мере увеличения длины провода. Такое увеличение разброса не случайно, и этому нет определенного объяснения.Как объяснялось выше, самое простое объяснение состоит в том, что между каждой записью в проводе образовывался фрагмент тепла, несмотря на меры предосторожности по отключению блока питания между каждым считыванием. Из этого нельзя сделать однозначного вывода, поскольку причина такого разброса неясна. Это ограничивает количество или детализацию выводов, которые можно сделать, и, следовательно, снижает сложность расследования, однако, если бы я повторно провел этот эксперимент, можно было бы оставить больше времени для охлаждения провода.Если бы тогда не было увеличения диапазона разброса, это дало бы достаточно свидетельств, подтверждающих это ранее описанное объяснение, и, следовательно, можно было бы сделать более уверенный вывод и подтвердить его точными данными. Чтобы продолжить эту часть исследования, я мог бы нарисовать график, который показал бы результаты вычислений n-го члена. Это позволило бы мне глубже проанализировать причины и причины небольшого увеличения значения «n» по мере увеличения длины.Это также позволило бы более наглядно отобразить тренд. Я также мог бы включить в график среднее значение «n». Я мог бы аннотировать график, чтобы более подробно объяснить, как работает это уравнение. Эксперимент 2 Во второй части исследования я собираюсь использовать несколько отрезков никель-хромовой проволоки разного диаметра, чтобы обнаружить любое изменение сопротивления между разными диаметрами проволоки. В этом втором эксперименте я решил использовать только 2 В постоянного тока, потому что тестовый провод был намного короче, чем в первом эксперименте. Чтобы результаты были максимально точными, каждое показание будет сниматься 3 раза, и на их основе будет рассчитываться среднее значение. Диаметр каждой проволоки будет рассчитан 3 раза, и будет принято среднее значение для обеспечения точных показаний. Это повысит точность и надежность записанных данных. Предварительный тест Я провел предварительный тест, чтобы убедиться, что вторая часть моего эксперимента будет работать и даст четкие результаты, которые показывают определенную тенденцию.Ширина никель-хромовой проволоки будет иметь значение для сопротивления проволоки, потому что в тонкой проволоке много электронов, которые должны перемещаться по пропорционально небольшому каналу. Это вызывает много столкновений с другими электронами. Это столкновение вызывает трение, которое выделяет тепло. Вырабатываемая тепловая энергия вызывает сопротивление, поскольку электрическая энергия тока преобразуется в тепловую. Эти факты подтверждаются данными результатов моего предварительного теста, показанными ниже.Сопротивление рассчитывалось по формуле V ÷ I = R. Диаметр провода (мм) Напряжение (В В) Ток (А) Сопротивление (Ом) Толстый 0,21 1,55 1,34 Тонкий 34 0,645 34 0,64513 Когда я проводил этот предварительный тест, я был абсолютно уверен, что мои результаты были точными, убедившись, что каждая длина провода была точно одинаковой длины, и я уменьшил входное напряжение с 12 В постоянного тока до 2 В постоянного тока. для того, чтобы провода, особенно более тонкие, не нагревались. Это изменило бы сопротивление проволоки, потому что чем больше тепловой энергии у проволоки, тем быстрее движутся атомы в ней, и поэтому электроны в токе имеют больше столкновений.Это вызывает трение, в результате которого выделяется тепло (см. Рис. 1 на стр. 3b во вводной части). Тепло производится за счет энергии электрического тока. Это приводит к увеличению общего сопротивления, поскольку у электрического тока отбирается энергия. Эти результаты показывают, что более толстая проволока имеет гораздо меньшее сопротивление, чем более тонкая проволока. Эти предварительные данные подтверждают мой первоначальный прогноз, в котором говорилось, что более тонкая проволока будет иметь большее сопротивление, чем более толстая. Я рассчитал сопротивление каждого провода по формуле R = V ÷ I.R — сопротивление в Ом, V — напряжение или разность потенциалов в вольтах, а «I» — ток, измеренный в амперах / амперах. Чем больше число Ом, тем выше сопротивление провода. При проведении предварительного теста я использовал следующие инструменты: источник питания (установлен на 2 В), 5 медных проводов, 2 зажима типа «крокодил», амперметр, вольтметр и никель-хромовые провода, толстые и тонкие. Метод Прибор для сбора: вольтметр, амперметр, 5 проводов, 2 зажима типа «крокодил», 7 нихромовых проводов разного диаметра и блок питания. Установите устройство, как показано: ЧЕРТЕЖ ЦЕПИ 2 Установите на блок питания как можно более низкое напряжение, 2 В. (Чтобы напряжение не приводило к нагреву провода.) Поместите нихром между двумя зажимами типа «крокодил», чтобы замкнуть цепь. Включите блок питания и запишите ток с амперметра и напряжение с вольтметра. Выключите блок питания. Повторите этот процесс для всех диаметров проволоки. Определите сопротивление для всех результатов, используя закон Ома. V = I * R Запишите результаты на график. Мои результаты оказались точными, потому что я провел тест 3 раза и рассчитал среднее значение с точностью до 2 знаков после запятой. Приведенные выше результаты являются средними значениями. Я также провел небольшой эксперимент, используя только 2 В постоянного тока, чтобы убедиться, что ни один из проводов не начал нагреваться. Чтобы повысить точность измерений диаметра каждой проволоки, я провел эксперимент, в котором каждую проволоку измеряли микрометром 3 раза.Микрометр зажимает проволоку между лицевой стороной шпинделя и лицевой стороной наковальни. Их регулируют вращением трещотки. Это перемещает шпиндель и наперсток вниз по втулке. На гильзе есть цифры, которые показывают диаметр проволоки при затяжке. Таблица результатов измерения проводов приведена ниже: Диаметр (мм) (2d.p) Тест 1 Тест 2 Тест 3 Среднее значение 0.25 0,26 0,22 0,24 0,35 0,32 24 0,34 24 0,34 24 0,34 0,34 0,58 0,56 0,71 0,69 0,69 0.69 0,88 0,89 0,88 0,88 0,90 0,90 1,20 1,19 1,21 1,20 . No related posts. Провод Похожие записи Сечение проводов по нагрузке: Калькулятор расчета сечения кабеля 03.09.2021 Соотношение тока и сечения провода: Соотношение сечения провода и мощности таблица 03.09.2021 Какой провод заземление в трехжильном проводе: Какой провод заземления в трехжильном проводе 02.09.2021 Проводка в деревянном: Электропроводка в деревянном доме своими руками 27.08.2021 Как подключить провода к автомату на щитке: Nothing found for Zashhita I Avtomatika Zashhita Do 1000V Kak V Shhitke Podklyuchit Avtomat 2480%23I 25.08.2021 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт +7 495 120-13-73, 8 800 500-97-74; [email protected] [email protected] Карта сайта