Соединение конденсаторов — Основы электроники

В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким обра­зом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллель­но, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока.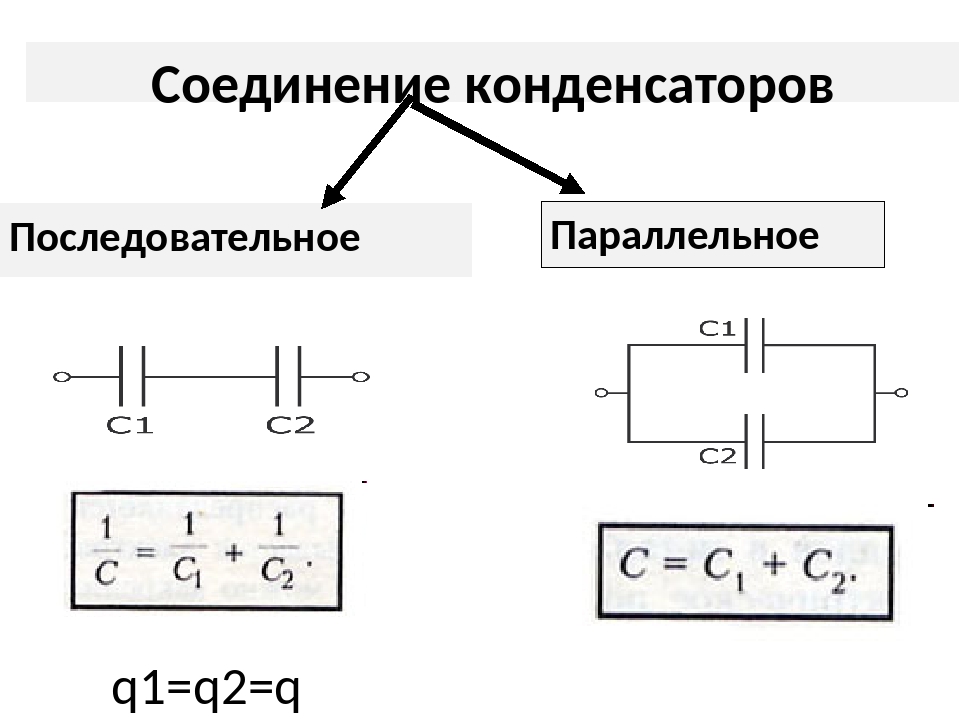

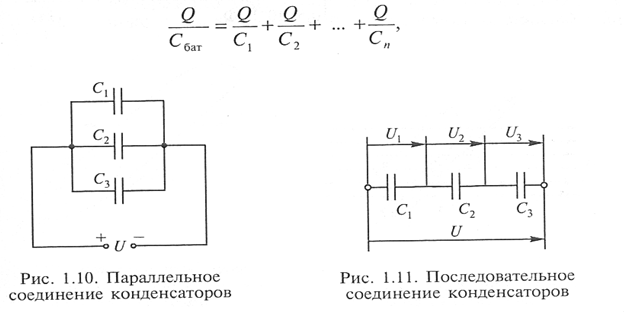
Общее же количе­ство электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из кон­денсаторов, так как заряд каждого их конденсаторов проис­ходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединен­ных конденсаторов можно рассматривать как один эквива­лентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов бук­вой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и во­обще при любом числе конденсаторов.

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последо­вательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденса­торы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заря­жаются через влияние. При этом заряд пла­стины 2 будет равен по величине и противо­положен по знаку за­ряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пла­стины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.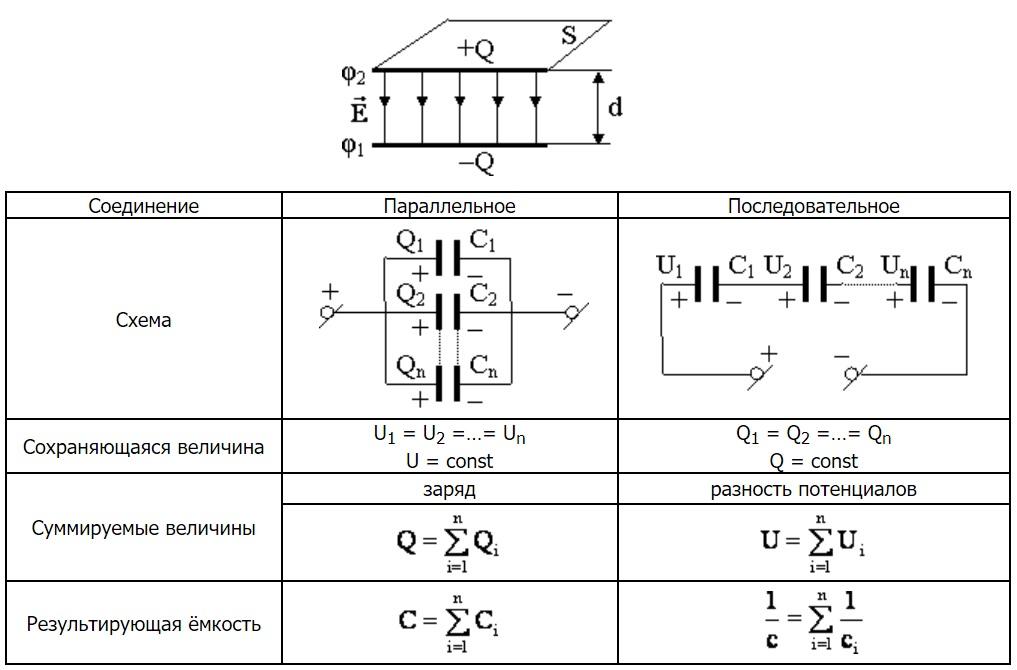

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряже­ния, существующего на всей группе конденсаторов. Напря­жение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединен­ных последовательно, меньше емкости самого малого конден­сатора в группе.

Для вычисления общей емкости при последовательном со­единении конденсаторов удобнее всего пользоваться следую­щей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельное (смешанное) соединение конденсаторов

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Рисунок 5.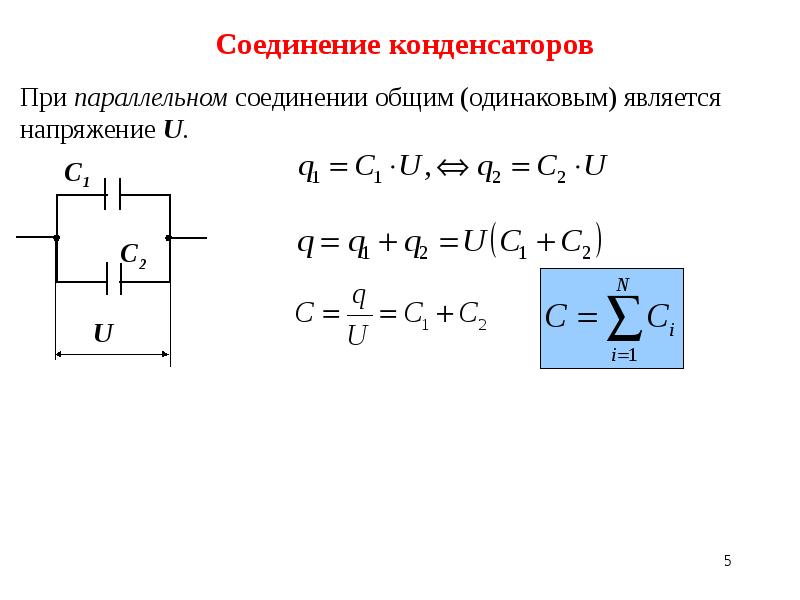

Пример расчета последовательно-параллельного соединения конденсаторов.

Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга.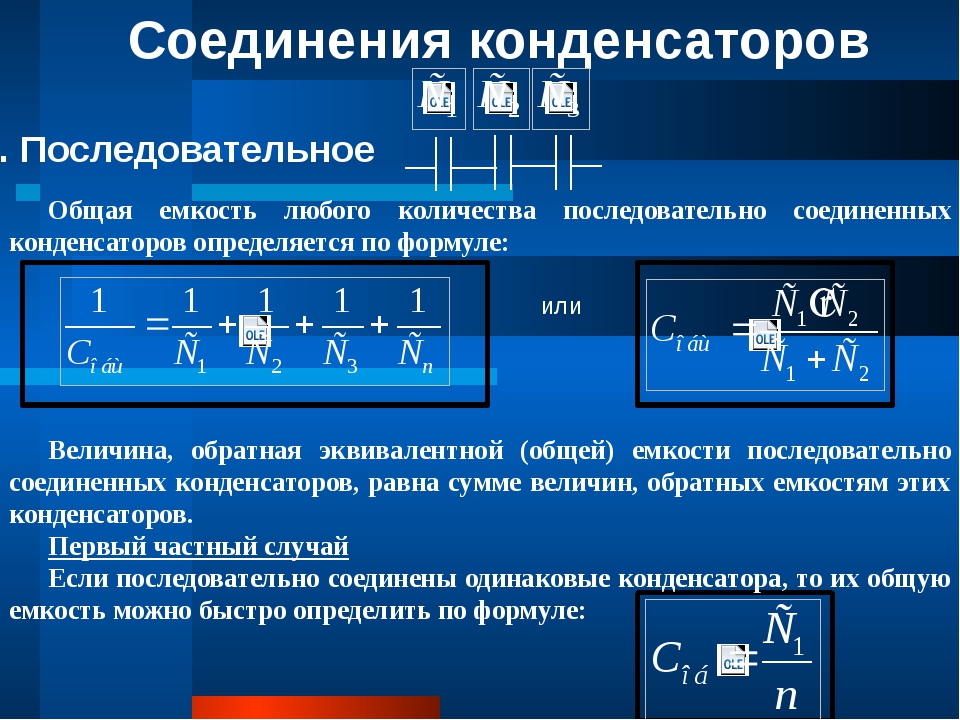 При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

Пример 1

Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С₁ = 10 мкФ, C₂ = 2 мкФ, C₃ = 5 мкФ, а C₄ = 1 мкФ?

При последовательном соединении общая емкость равна:

При параллельном соединении общая емкость равна:

Пример 2

Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С₁ = 7 мкФ, С₂ = 2 мкФ, С

3 = 1 мкФ.

Сначала найдем общую емкость параллельного участка цепи:

Затем найдем общую емкость для всей цепи:

По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Советуем прочесть — Заряд и разряд конденсатора

Просмотров:

Последовательное и параллельное соединение конденсаторов

Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.

Емкость набора при последовательном соединении конденсаторов будет вычисляться по формуле:

	1	=	1	+	1	+	1	+ . ..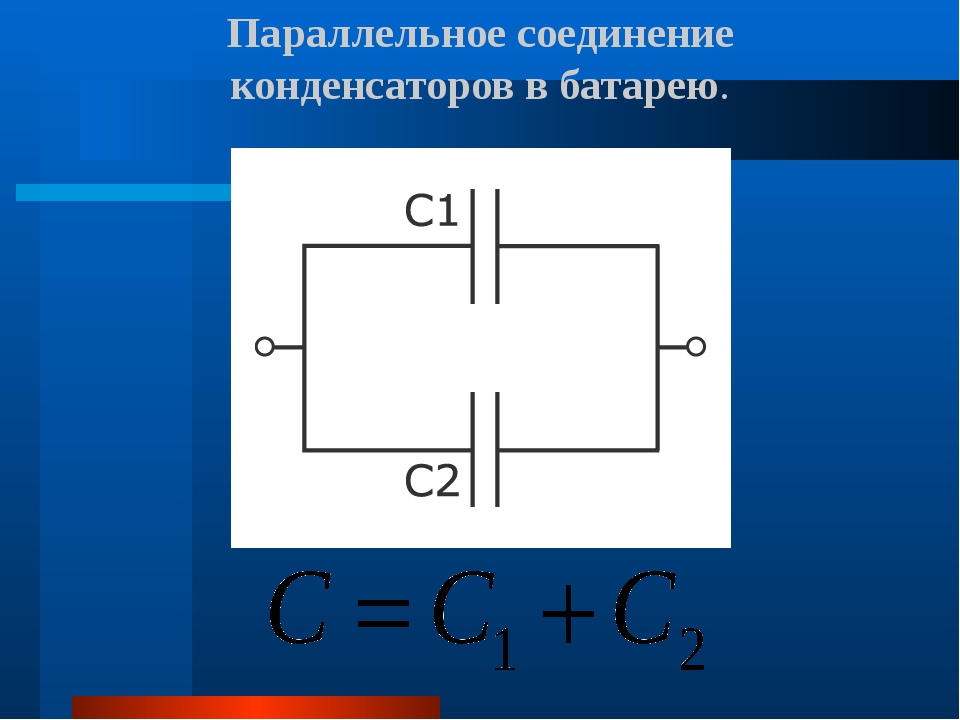
	C		C1		C2		C3

А общее напряжение будет равняться сумме напряжений всех конденсаторов.
Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый. При их последовательном соединении общий конденсатор будет иметь следующие данные: 10 мкФ x 300 В.

При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора.

C = C1 + C2 + C3 + C4 + …

Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В.

Соединение более двух конденсаторов последовательно редко встречается в реальных схемах. Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления.

Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратны формулам вычисления сопротивления при последовательном и параллельном соединении резисторов.

Параллельное и последовательное соединение конденсаторов.

Всем привет. Этот маленький пост посвящу теме соединения конденсаторов.

На практике,  часто бывает так, что в наличии нет конденсатора нужного номинала для установки, а технику нужно срочно отремонтировать.  Как раз для таких случаев нам необходимы знания о правилах соединения конденсаторов.

Способов соединения конденсаторов существуют всего два. Это последовательное и параллельное соединение. Сейчас более детально рассмотрим оба способа.

Параллельное  соединение конденсаторов.

Это наиболее частый вид соединения конденсаторов.  При подключении параллельно, емкость конденсатора увеличивается, а напряжение остается прежним.

Формула параллельного соединения конденсаторов: С= С1+С2+С3…

Рассмотрим на примере. Предположим, что необходим конденсатор 100 мкф 50в, а у Вас в наличии только 47мкф на 50в. Если соединить эти конденсаторы параллельно (плюс к плюсу а  минус к минусу) то общая емкость  получившегося конденсатора будет ровняться  около 94 мкф на 50в. Это допустимое отклонение, так что можно свободно устанавливать  в технику.

Параллельное соединение конденсаторов

 

Последовательное  соединение конденсаторов.

При подключении, таким образом, общая емкость уменьшается, а напряжение работы конденсатора растёт.

Рассчитывается последовательное  подключение конденсаторов по такой формуле:

Формула расчета последовательного соединения конденсаторов

Для примера подключим  3 конденсатора номиналом  100мкф на 100в последовательно. Согласно формуле, делим единицу, на емкость конденсаторов. Потом суммируем . Далее единицу делим на результат.

(1:100)+(1:100)+(1:100) = 0,01 + 0,01 + 0,01 = 0,03  далее 1 : 0,03 = 33 мкф на 300вольт (напряжение суммируем  100+100+100 = 300в). Итого 33мкф на 300в.

В работе, последовательное соединение использую редко, но иногда бывает.

Рекомендую ознакомиться со статей  о ESR конденсаторов.

Всем спасибо за просмотр.

---

---

Весь инструмент и расходники, которые я использую в ремонтах находится здесь.

---

Если у Вас возникли вопросы по ремонту телевизионной техники, вы можете задать их на нашем новом форуме .

---

Загрузка. ..

Соединение конденсаторов.

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С₁ – ёмкость первого;

С₂ – ёмкость второго;

С₃ – ёмкость третьего;

С_N – ёмкость N-ого конденсатора;

C_общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C₁, C₂ в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула.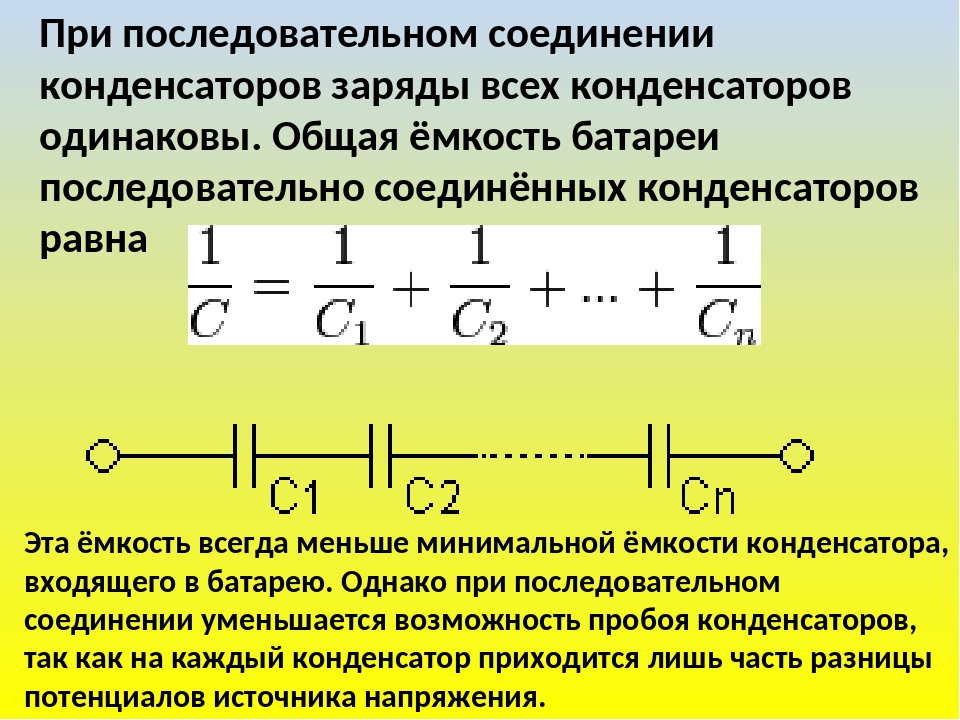 Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C₁ – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение.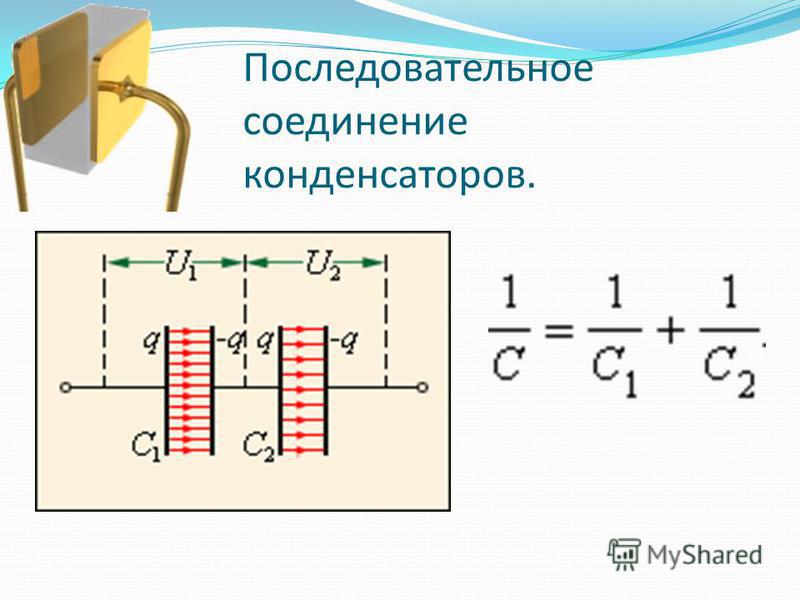 При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

 

Параллельное и последовательное соединение конденсаторов

Элементы цепи могут быть подключены двумя способами:

1. последовательно
2. параллельно

Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).

• последовательное соединение конденсаторов

Рис. 1. Последовательное соединение конденсаторов

Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).

Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).

Рис. 2. Последовательное соединение конденсаторов

Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — 

(помним, что они одинаковы), электроёмкости — ,  и соответствующие напряжения —  и .

Учитывая определение электроёмкости:

 (1)

Тогда:

 (2)

 (3)

 (4)

Памятуя о том, что конденсаторы соединены последовательно, получаем:

 (5)

Тогда:

 (6)

Или в общем виде:

(7)

• где
  • — электроёмкость последовательно соединённых конденсаторов,
  • — сумма обратных емкостей.

Для цепи из двух последовательных соединений:

(8)

•  параллельное соединение конденсаторов

Рис. 3. Параллельное соединение конденсаторов

Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.

Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости

Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:

(9)

(10)

(11)

С учётом того, что 

, получим:

(12)

Сокращаем:

(13)

Или в общем виде:

(14)

• где
  • —  электроёмкость параллельно соединённых конденсаторов,
  • — сумма электроёмкостей последовательно соединённой цепи.

Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:

• для последовательного соединения
• для параллельного соединения

Поделиться ссылкой:

Соединение конденсаторов: последовательное, параллельное и смешанное

В электротехнике существуют различные варианты подключения электрических элементов.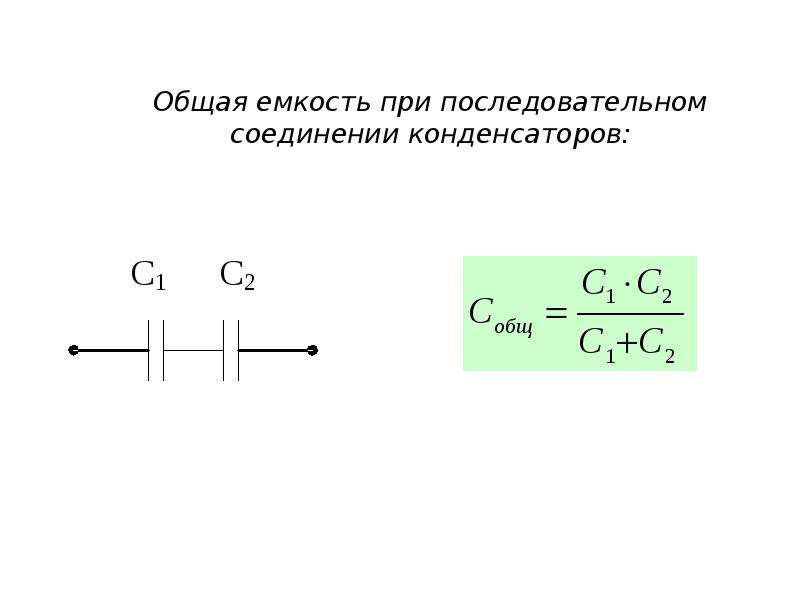 В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.

Параллельное соединение

Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии

Схема параллельного крепления

 

Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.

C_общ = C₁ + C₂ + C₃

Схема — напряжение на накопителях

 

В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:

V_AB = V_C1 = V_C2 = V_C3 = 20 Вольт

Последовательное соединение

Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.

Схема — схема последовательного соединения

 

Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.

Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:

i = i_c1 = i_c2 = i_c3 = i_c4, то есть токи проходящие через каждый конденсатор равны между собой.

Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:

Q_общ= Q₁ = Q₂ = Q₃

А так определяется общая суммарная емкость конденсаторов при последовательном соединении:

1/C_общ = 1/C₁ + 1/C₂ + 1/C₃

Видео: как соединять конденсаторы параллельным и последовательным методом

Смешанное подключение

Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.

Схема: смешанное соединение конденсаторов

Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:

1. Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
2. Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
3. Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
4. Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.

8.3: Последовательные и параллельные конденсаторы

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях. Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость.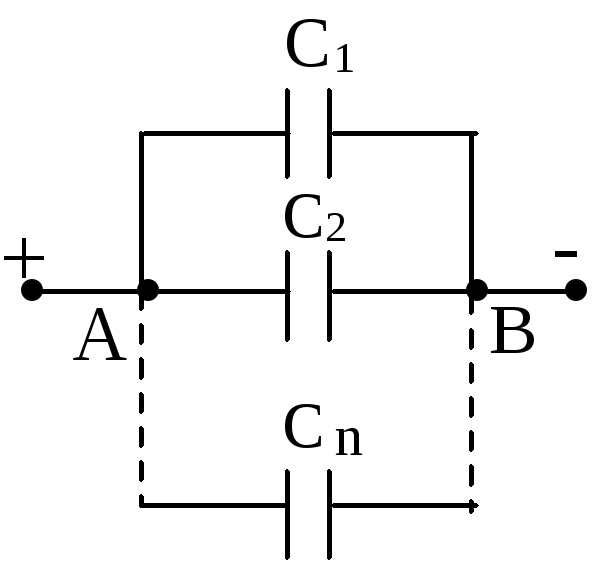 Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы. Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:

\ [C = \ dfrac {Q} {V}. \]

Когда эта последовательная комбинация подключена к батарее с напряжением В , каждый из конденсаторов получает одинаковый заряд Q .Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд .Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.

Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен В.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:

\ [V = V_1 + V_2 + V_3. \]

Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \).Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем

\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]

Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}. \]

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.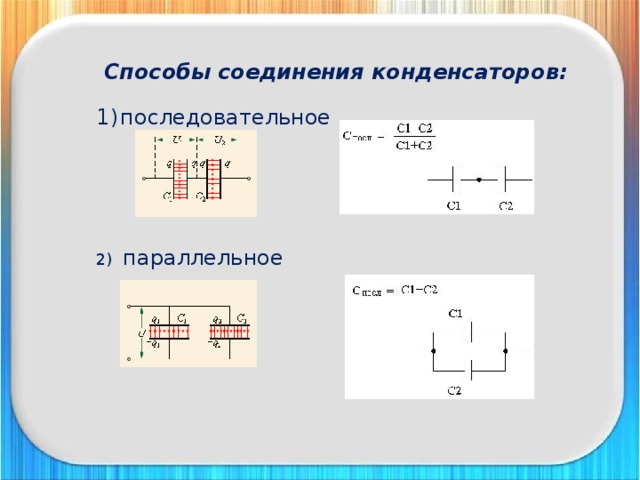

Комбинация серии

Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, является суммой обратных величин индивидуальных емкостей:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]

Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.

Решение

Вводим указанные емкости в уравнение \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1. 000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]

Теперь инвертируем этот результат и получаем

\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:

\ [Q = Q_1 + Q_2 + Q_3. \]

В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем

\ [C_pV = C_1V + C_2V + C_3V. \]

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

\ [C_p = C_1 + C_2 + C_3. \]

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]

Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.

Решение

Ввод заданных емкостей в уравнение \ ref {capparallel} дает

\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).

Пример \ (\ PageIndex {3} \): эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.

Стратегия

Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, обозначенная \ (C_S \), параллельна \ (C_3 \).

Решение

Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]

Для этого

\ [C_S = 0,833 \ mu F. \ nonumber \]

Емкость \ (C_S \) подключена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:

\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.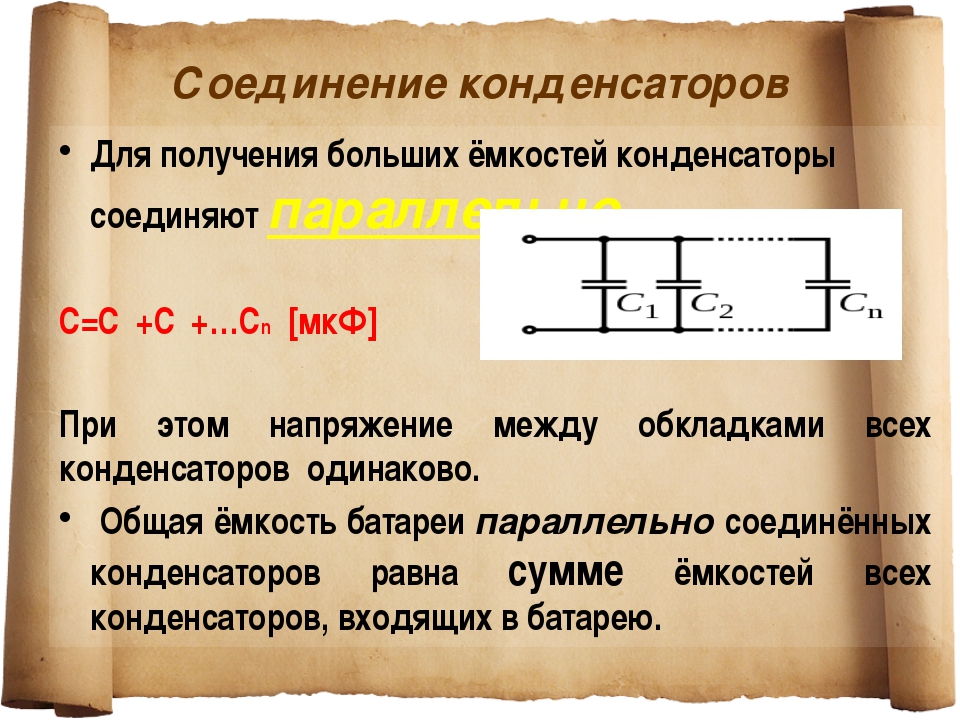 833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.

Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия

Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.

Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет

\ [C_ {23} = C_2 + C_3 = 2. 0 мк F + 4,0 мк F = 6,0 мк F. \]

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому

\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]

Теперь разность потенциалов на конденсаторе 1 равна

.

\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48.0 \ mu C} {12.0 \ mu F} = 4.0 V. \]

Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:

\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]

\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]

Значение Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)

Упражнение \ (\ PageIndex {1} \)

Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.

Ответьте на

\ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)

Ответ b

\ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)

Ответ c

\ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)

конденсаторов последовательно и параллельно

конденсаторов последовательно и параллельно
Далее: Энергия в конденсаторах Up: Емкость Предыдущая: Диэлектрики Конденсаторы — один из стандартных компонентов электронных схем. Кроме того, часто встречаются сложные комбинации конденсаторов. в практических схемах. Это, поэтому полезно иметь набор правил для определения эквивалентной емкости некоторого общего расположения конденсаторов. Оказывается, всегда можно найти эквивалентная емкость при повторном применение два простых правил. Эти правила относятся к подключенным конденсаторам. последовательно и параллельно.

Рисунок 15: Два конденсатора подключены параллельно.

Рассмотрим два конденсатора, подключенных параллельно : , т.е. , с положительно заряженные пластины подключены к общему « входному » проводу, а отрицательно заряженные пластины присоединены к общему « выходному » проводу — см. рис. 15. Какая эквивалентная емкость между входным и выходным проводами? В этом случае потенциал разница между двумя конденсаторами одинакова и равна разность потенциалов между входным и выходным проводами. Общий заряд однако, хранящиеся в двух конденсаторах делятся между конденсаторы, так как он должен распределяться так, чтобы напряжение на два то же самое. Поскольку конденсаторы могут иметь разную емкость, и, и сборы тоже могут быть разными. Эквивалентная емкость пары конденсаторов — это просто соотношение, где — общий накопленный заряд. Следует, что

(113)

давая

(114)

Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех конденсаторы.Таким образом, правило таково:

Эквивалентная емкость двух конденсаторов, соединенных параллельно представляет собой сумму отдельных емкостей.

Для конденсаторов, соединенных параллельно, уравнение. (114) обобщает на .

Рисунок 16: Два конденсатора, соединенных последовательно.

Рассмотрим два конденсатора, подключенных в серию : , т. Е. , в линию так, что положительная пластина одного прикреплена к отрицательной пластине другого — см. Инжир.16. Фактически, предположим, что положительная обкладка конденсатора 1 подключена к проводу « вход » отрицательная обкладка конденсатора 1 подключается к положительная пластина конденсатора 2 и отрицательная пластина конденсатора 2 подключается к проводу « выход ». Какая эквивалентная емкость между входными и выходными проводами? В этом случае важно понимать, что заряд, хранящийся в два конденсатора одинаковые. Это легче всего увидеть, если рассмотреть « внутренние » пластины: i.е. , отрицательная обкладка конденсатора 1, и положительная пластина конденсатора 2. Эти пластины физически отключены. от остальной части схемы, поэтому общий заряд на них должен остается постоянным. Если предположить, что кажется разумным, что эти пластины несут нулевой заряд когда к двум конденсаторам приложена нулевая разность потенциалов, следует что при наличии ненулевой разности потенциалов заряд на положительном пластина конденсатора 2 должна быть сбалансирована равным и противоположным зарядом на отрицательной пластине конденсатора 1.Поскольку отрицательная пластина Конденсатор 1 несет заряд, положительная пластина должна нести заряд. Аналогичным образом, поскольку положительная пластина конденсатора 2 несет заряд, отрицательная пластина должна нести заряд. В итоге оба конденсатора обладают таким же накопленным зарядом. Потенциал падает, и два конденсатора, как правило, разные. Однако сумма этих падение равняется общему падению потенциала, приложенному на входе и выходе провода: т.е. ,. Эквивалентная емкость пары конденсаторы снова .Таким образом,

(115)

давая

(116)

Здесь мы воспользовались тем фактом, что заряд является общим для всех трех конденсаторы. Следовательно, правило таково:

Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в серия — это сумма обратных величин отдельных емкостей.

Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на

---

Далее: Энергия в конденсаторах Up: Емкость Предыдущая: Диэлектрики

Ричард Фицпатрик 2007-07-14

4.2 Последовательные и параллельные конденсаторы — Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Объясните, как определить эквивалентную емкость конденсаторов, соединенных последовательно и параллельно
• Вычислить разность потенциалов на пластинах и заряд на пластинах конденсатора в сети и определить полезную емкость сети конденсаторов.

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях. Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

Рисунок 4.2.1 иллюстрирует последовательную комбинацию трех конденсаторов, расположенных в ряд внутри схемы. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 4.1.1. Когда эта последовательная комбинация подключена к аккумулятору с напряжением В, , каждый из конденсаторов приобретает идентичный заряд. Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме аккумулятора, есть, а заряд на пластине, подключенной к отрицательной клемме. Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала на одном конденсаторе может отличаться от падения потенциала на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд в последовательной цепи снимается с пластины первого конденсатора (который мы обозначаем как), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как), и так далее.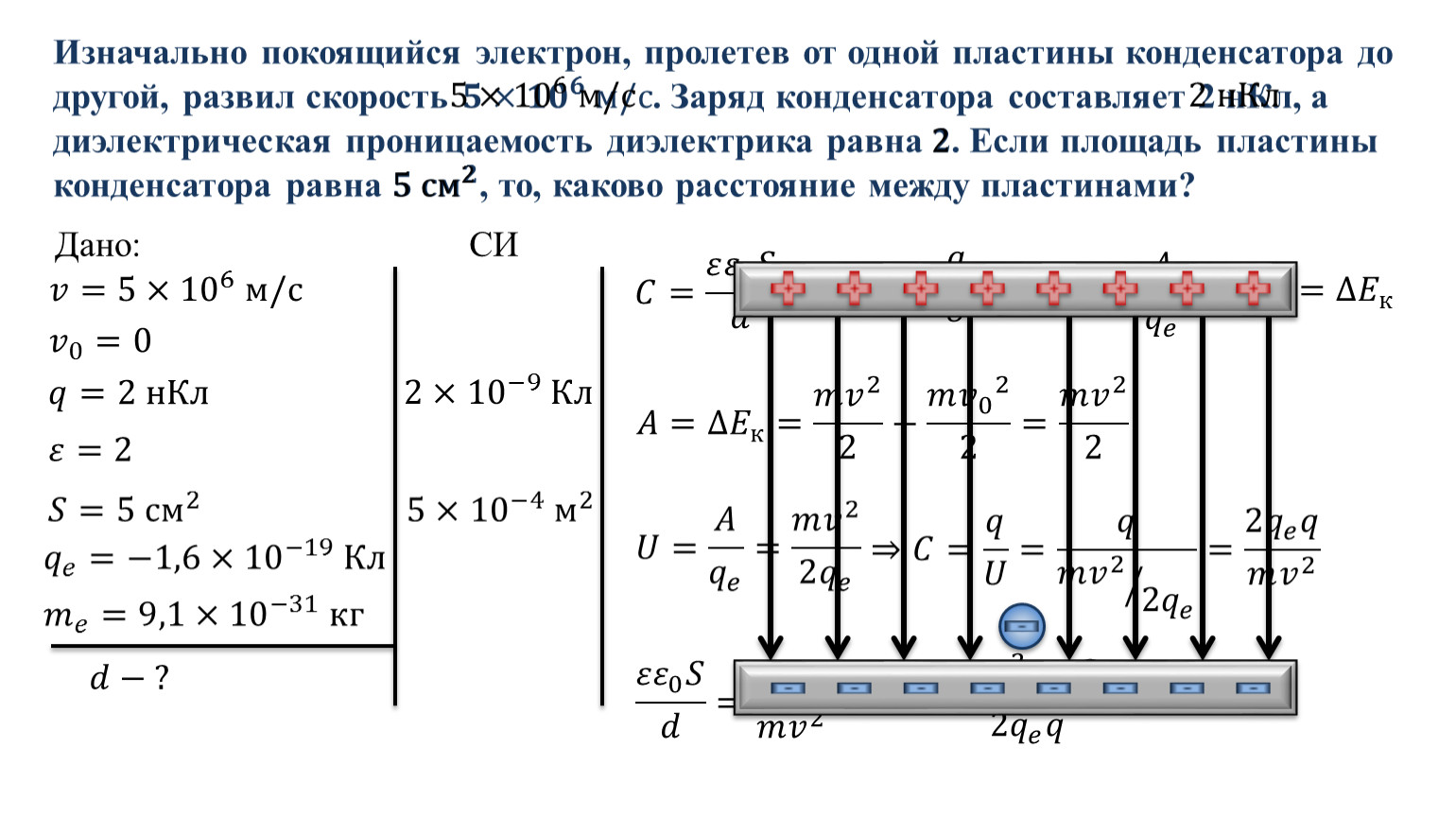

(рисунок 4.2.1)

Рисунок 4.2.1 (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине. (б) Сеть конденсаторов в (а) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей в (а), и заряд на его пластинах равен.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах, и равны, соответственно,, и ,. Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:

Потенциал измеряется на эквивалентном конденсаторе, который держит заряд и имеет эквивалентную емкость.Вводя выражения для, и, получаем

Отменяя заряд, получаем выражение, содержащее эквивалентную емкость трех последовательно соединенных конденсаторов:

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.

КОМБИНАЦИЯ СЕРИИ

---

Для конденсаторов, соединенных в комбинацию серии , величина, обратная эквивалентной емкости, является суммой обратных величин индивидуальных емкостей:

(4. 2.1)

ПРИМЕР 4.2.1

---

Эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны, и.

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.1 с тремя членами.

Решение

Мы вводим указанные емкости в уравнение 4.2.1:

Теперь инвертируем этот результат и получаем.

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке 4.2.2 (а). Поскольку конденсаторы соединены параллельно, , все они имеют одинаковое напряжение на пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость параллельной сети, отметим, что общий заряд, накопленный в сети, представляет собой сумму всех отдельных зарядов:

В левой части этого уравнения используется соотношение, которое справедливо для всей сети. В правой части уравнения мы используем соотношения, и для трех конденсаторов в сети.Таким образом получаем

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

ПАРАЛЛЕЛЬНАЯ КОМБИНАЦИЯ

---

Для конденсаторов, соединенных в параллельную комбинацию , эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

(4.2.2)

(рисунок 4.2.2)

Рисунок 4. 2.2 (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

ПРИМЕР 4.2.2

---

Эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая их индивидуальные емкости, и.

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.2 с тремя членами.

Решение

Ввод заданных емкостей в уравнение 4.2.2 дает

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на рисунке 4.2.3. Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

(рисунок 4.2.3)

ПРИМЕР 4.2.4

---

Сеть конденсаторов

Определите полезную емкость комбинации конденсаторов, показанной на рисунке 4.2.4 при емкостях,,. Когда в комбинации сохраняется разность потенциалов, найдите заряд и напряжение на каждом конденсаторе.

(рисунок 4.2.4)

Рисунок 4.2.4 (a) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.

Стратегия

Сначала мы вычисляем полезную емкость параллельного соединения и. Тогда — чистая емкость последовательного соединения и. Мы используем соотношение, чтобы найти заряды, и, и напряжения,, и на конденсаторах, и, соответственно.

Решение

Эквивалентная емкость для и составляет

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 4.2.4 (b). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд,. Кроме того, конденсаторы разделяют разность потенциалов, поэтому

Теперь разность потенциалов на конденсаторе

.

Поскольку конденсаторы и подключены параллельно, они имеют одинаковую разность потенциалов:

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

Значение

Как и ожидалось, чистая плата за параллельную комбинацию и составляет.

ПРОВЕРЬТЕ ПОНИМАНИЕ 4.5

---

Кандела Цитаты

Лицензионный контент CC, особая атрибуция

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

Последовательные и параллельные конденсаторы

Последовательные и параллельные конденсаторы

Конденсаторы могут быть подключены последовательно или параллельно для получения результирующего значения, которое может быть либо суммой отдельных значений (параллельно), либо значением меньше, чем у наименьшая емкость (последовательно).

КОНДЕНСАТОРЫ СЕРИИ

Общий эффект последовательного соединения конденсаторов заключается в перемещении пластин конденсаторы дальше друг от друга. Это показано на рисунке 3-13. Обратите внимание, что стык между C1 и C2 имеют как отрицательный, так и положительный заряд. Это приводит к тому, что соединение становится по сути нейтрально. Общая емкость цепи развита между левыми пластина С1 и правая пластина С2. Поскольку эти пластины расположены дальше друг от друга, общая значение емкости в цепи уменьшается.Решение для общей емкости (C _T ) конденсаторов, соединенных последовательно, аналогично решению для общего сопротивления (R _T ) резисторы подключены параллельно.

Рисунок 3-13. — Конденсаторы последовательно.

Обратите внимание на сходство формул для R _T и C _T :

Если в цепи больше двух конденсаторов, используйте приведенную выше формулу. Если схема содержит только два конденсатора, используйте следующую формулу:

Примечание. Все значения для C _T , C1, C2, C3, … C _n должны быть в фарадах. Из приведенных выше формул должно быть очевидно, что общая емкость конденсаторов в серия меньше, чем емкость любого из отдельных конденсаторов.

Пример: определить общую емкость последовательной цепи, содержащей три конденсаторы, номинал которых равен 0.01 мФ, 0,25 мФ, и 50 000 пФ соответственно.

Общая емкость 0,008 мФ немного меньше, чем самый маленький конденсатор (0,01мФ).

КОНДЕНСАТОРЫ ПАРАЛЛЕЛЬНО

При параллельном подключении конденсаторов подключается по одной пластине каждого конденсатора. непосредственно к одному выводу источника, в то время как другая обкладка каждого конденсатора подключен к другому терминалу источника.На Рис. 3-14 показаны все отрицательные пластины. конденсаторов, соединенных вместе, и всех положительных обкладок, соединенных вместе. C _{Таким образом, T} выглядит как конденсатор с площадью пластины, равной сумме всех отдельные участки пластины. Как упоминалось ранее, емкость является прямой функцией пластины. область. Параллельное подключение конденсаторов эффективно увеличивает площадь пластины и, следовательно, увеличивает общую емкость.

Рисунок 3-14. — Параллельная емкостная цепь.

Для конденсаторов, соединенных параллельно, общая емкость является суммой всех индивидуальные емкости. Полная емкость цепи может быть рассчитана с использованием формула:

, где все емкости указаны в одних и тех же единицах.

Пример: определение общей емкости в параллельной емкостной цепи, содержащей три конденсатора, номинал которых равен 0.03 мФ, 2,0 мФ и 0,25 мФ соответственно.

Q.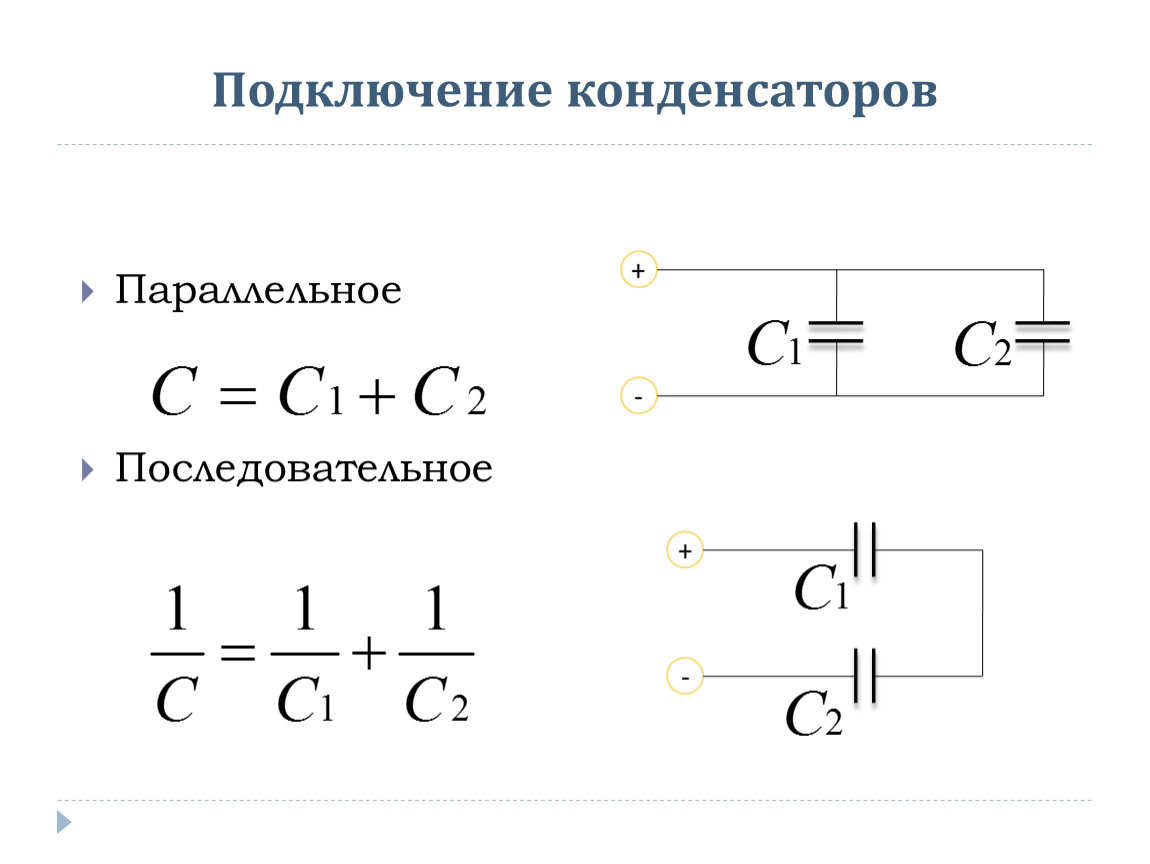 16 Какова общая емкость цепи, содержащей два последовательно соединенных конденсатора (10 мФ и 0,1 мФ)?
В.17 Какова общая емкость цепи, в которой четыре конденсатора (10 мФ, 21 мФ, 0,1 мФ и 2 мФ) подключены параллельно?

Цепи конденсаторов серии

и параллельные

Разница между Кулоном и Фарадом

Раньше переходя к последовательным и параллельным цепям конденсаторов, сначала посмотрите на разница между кулоном и фарадом, потому что многие люди запутаться в определении разницы между кулоном и Фарад.

Электрический заряд измеряется в кулонах. Один кулон (1С) равен равно количеству заряда, передаваемого за одну секунду Текущий одного Ампера (1А).

Емкость является способность тела или устройства накапливать электрический заряд. Емкость измеряется в фарадах (Ф). Устройство с большим Емкость (96F) сохранит большой заряд.Точно так же устройство с малой емкостью (1F) будет хранить небольшая сумма заряда.

серии конденсаторная схема

А последовательный конденсатор схема — это электронная схема, в которой все конденсаторы подключаются друг за другом по одному и тому же пути, поэтому что к каждому конденсатору протекает одинаковый заряд или ток.

общая емкость цепи последовательного конденсатора получается как сложение обратных величин (1 / C) значений емкости отдельных конденсаторов, а затем взяв обратную величину Общая.

Для Например, если три конденсатора соединены последовательно. Тогда общая емкость цепи

Все ток или заряд, протекающий через первый конденсатор, другого пути нет.Следовательно, он также должен проходить через второй конденсатор, третий конденсатор, четвертый конденсатор и т. д. на.

Пример:

А Схема последовательного конденсатора показана на рисунке ниже. В схема состоит из трех конденсаторов, которые включены в последовательный и источник постоянного напряжения.

емкости из трех конденсаторов: C ₁ = 2F, C ₂ = 4F, C ₃ = 6F и постоянное напряжение = 10 В.

Как как показано на рисунке, положительный полюс батареи постоянного тока подключается к правой боковой пластине конденсатора С ₃ отрицательная клемма батареи постоянного тока подключена к левая боковая пластина конденсатора С ₁ .

Когда а напряжение приложено к цепи, отрицательные заряды в правой боковой пластине конденсатора С ₃ находятся притянул к плюсовой клемме аккума.Это вызывает недостаток отрицательных зарядов в правой боковой пластине C ₃ . В итоге правая боковая пластина конденсатора С ₃ заряжен положительно.

Аналогично, в положительные заряды в левой боковой пластине конденсатора С ₁ притягиваются к отрицательной клемме аккумулятора. Этот вызывает нехватку положительных зарядов в левой боковой пластине из C ₁ .В результате левая боковая пластина конденсатор С ₁ заряжен отрицательно.

отрицательные заряды в левой боковой пластине конденсатора С ₁ отталкивать отрицательные заряды в правой боковой пластине конденсатор С ₁ . Это вызывает отрицательные заряды. сток с правой боковой пластины конденсатора С ₁ к левой боковой пластине конденсатора С ₂ .Как В результате правая боковая пластина конденсатора С ₁ оказывается положительно заряжена и левая боковая пластина конденсатора С ₂ заряжен отрицательно.

отрицательные заряды в левой боковой пластине конденсатора С ₂ отталкивать отрицательные заряды в правой боковой пластине конденсатор С ₂ .Это вызывает отрицательные заряды. сток с правой боковой пластины конденсатора С ₂ к левой боковой пластине конденсатора С ₃ . Как В результате правая боковая пластина конденсатора С ₂ оказывается положительно заряжена и левая боковая пластина конденсатора С ₃ заряжен отрицательно.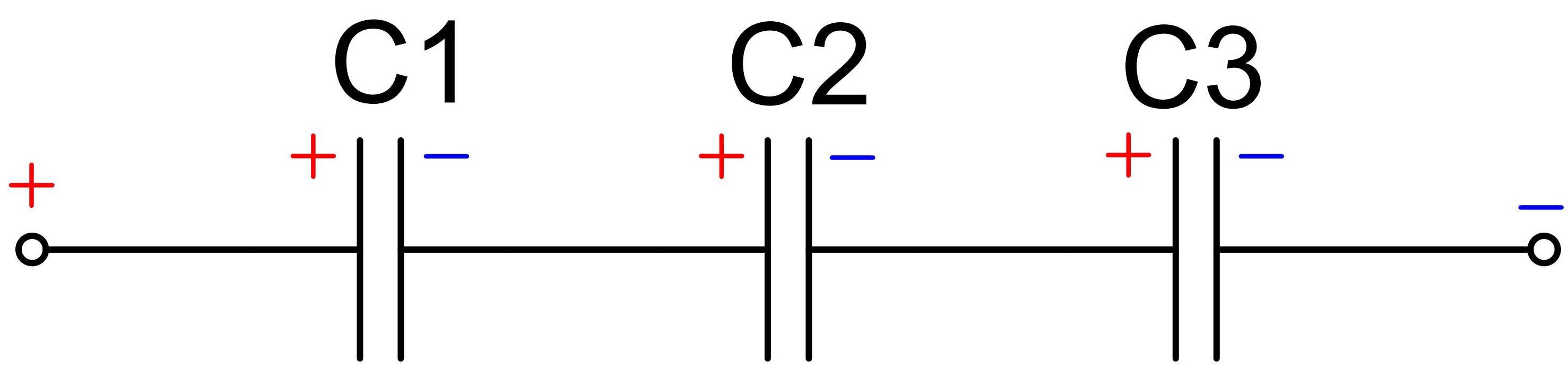

Таким образом, все три конденсатора заряжаются.

ср знайте, что ток означает поток заряда. С того же ток течет через все три конденсатора, поэтому каждый конденсатор будет держать такой же заряд. Это означает, что если один конденсатор держит заряд 2C, тогда остальные конденсаторы тоже держит такой же заряд 2С.

Так если вы обнаружите заряд на одном из конденсаторов, у вас нашел заряд на всех оставшихся конденсаторах.

В чтобы найти заряд на каждом конденсаторе, сначала нам нужно найти общую емкость или эквивалентную емкость.

общая емкость эквивалентного конденсатора

Автор используя формулу C = Q / V, легко найти заряд хранится на эквивалентном конденсаторе.

Начисление на каждого физ. конденсаторы, подключенные последовательно, такие же, как заряд на эквиваленте конденсатор.

Итак, так как заряд на эквивалент конденсатор был 10,91 кулонов, заряд на каждой из отдельные конденсаторы, включенные последовательно, будут иметь 10,91 кулонов.

Следовательно,

Плата за C ₁ = 10.91 C

Заряд на C ₂ = 10.91 C

Заряд на C ₃ = 10.91 С

Однако в цепи последовательного конденсатора напряжение на каждом индивидуальный конденсатор разный.

ср легко найти напряжение на каждом отдельном конденсаторе по формуле C = Q / V

емкость и заряд на каждом отдельном конденсаторе известны. Итак, мы нужно найти неизвестное напряжение.

В = Q / C

напряжение на конденсаторе (C ₁ ) составляет В ₁ = Q / C ₁ = 10,91 / 2 = 5,455 В

напряжение на конденсаторе (C ₂ ) составляет В ₂ = Q / C ₂ = 10,91 / 4 = 2,727 В

напряжение на конденсаторе (C ₃ ) составляет V ₃ = Q / С ₃ = 10.91/6 = 1,818 В

полное напряжение в цепи последовательного конденсатора равно сумма всех отдельных напряжений, сложенных вместе.

Т.е. V = V ₁ + V ₂ + V ₃ = 5,455 + 2,727 + 1,818 = 10 В

Параллельный конденсаторная схема

А параллельная конденсаторная схема — это электронная схема, в которой все конденсаторы подключены бок о бок в разных пути, чтобы тот же заряд или ток не проходили через каждый конденсатор.

Когда на параллельную цепь подается напряжение, каждый конденсатор получит другой заряд. Конденсатор с высоким емкость получит больший заряд, тогда как конденсатор с чем меньше емкость, тем меньше будет заряда. Например, восьмерка Фарадный конденсатор (8F) получит больше заряда, чем четыре фарада конденсатор (4Ф) попадает.

Путь конденсаторы параллельно будет увеличиваться размер пластин конденсатора без увеличения расстояния между ними. Итак, общая емкость параллельной конденсаторной цепи получается просто суммируя значения емкости отдельных конденсаторы.

Пример:

А Схема параллельного конденсатора показана на рисунке ниже.В схема состоит из трех конденсаторов, которые включены в параллельный и источник постоянного напряжения.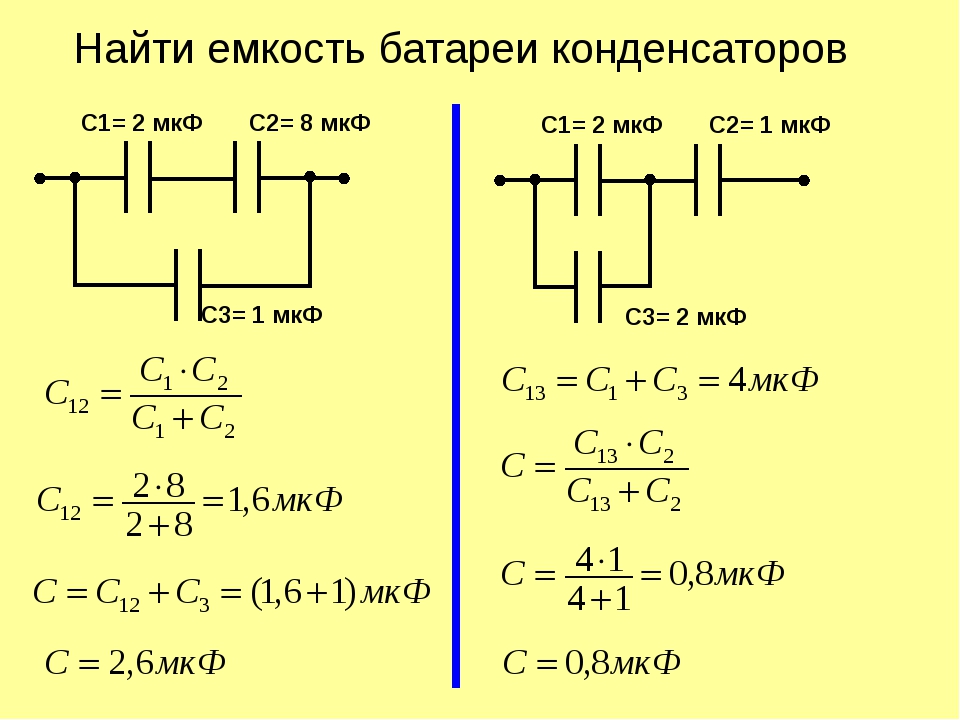

Если Значения трех конденсаторов: C ₁ = 8F, C ₂ = 4F, C ₃ = 2F и батарея постоянного тока = 10 В, тогда

общая емкость составляет C _T = C ₁ + C ₂ + C ₃ = 8 + 4 + 2 = 14F

В Принципиальная схема, нижние обкладки трех конденсаторов напрямую подключены к положительной клемме аккумулятора а верхние обкладки трех конденсаторов непосредственно подключен к отрицательной клемме аккумуляторной батареи.Следовательно, напряжение на всех трех конденсаторах одинаковое, что составляет равно напряжению АКБ постоянного тока (10 В).

Однако в параллельной цепи конденсаторов заряд сохраняется на каждом конденсатор будет другим.

Автор используя формулу емкости, легко найти заряд хранится на каждом конденсаторе.

И.е. C = Q / V

Q = C × V

заряд, накопленный на конденсаторе (C ₁ ), составляет Q ₁ = С ₁ × V = 8 × 10 = 80 С

заряд, накопленный на конденсаторе (C ₂ ), составляет Q ₂ = С ₂ × V = 4 × 10 = 40 С

Заряд, накопленный на конденсаторе (C ₃ ), составляет Q ₃ = C ₃ × V = 2 × 10 = 20 С

Общий заряд, хранящийся в параллельном конденсаторная цепь равна сумме всех отдельных заряды конденсатора складываются.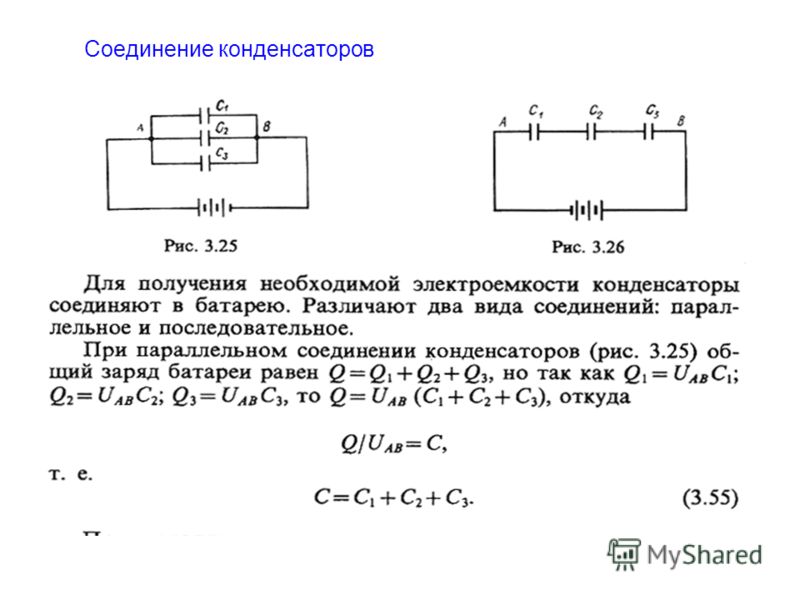

Т.е. Q _T = Q ₁ + Q ₂ + Q ₃ = 80 + 40 + 20 = 140 C

19.6 Последовательные и параллельные конденсаторы — College Physics chapters 1-17

Сводка

• Выведите выражения для полной емкости последовательно и параллельно.
• Обозначение последовательной и параллельной частей в комбинации подключения конденсаторов.
• Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа соединений: , , , и , , параллельный, , , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с последовательными и параллельными соединениями.

На рисунке 1 (а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] \ boldsymbol {C = \ frac {Q} {V}} [/ latex].

Обратите внимание на рис. 1, что противоположные заряды величиной [латекс] \ boldsymbol {Q} [/ latex] текут по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс] \ boldsymbol {V} [/ латекс] . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1 (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине — Q . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [latex] \ boldsymbol {C = \ frac {Q} {V}} [/ latex] для [latex] \ boldsymbol {V} [/ latex] дает [латекс] \ boldsymbol {V = \ frac {Q} {C}} [/ latex]. Таким образом, напряжения на отдельных конденсаторах составляют [латекс] \ boldsymbol {V_1 = \ frac {Q} {C_1}} [/ latex], [латекс] \ boldsymbol {V_2 = \ frac {Q} {C_2}} [/ латекс ] и [латекс] \ boldsymbol {V_3 = \ frac {Q} {C_3}} [/ latex]. Общее напряжение складывается из отдельных напряжений:

[латекс] \ boldsymbol {V = V_1 + V_2 + V_3}.[/ латекс]

Теперь, называя общую емкость [латекс] \ boldsymbol {C_S} [/ latex] для последовательной емкости, примите во внимание, что

[латекс] \ boldsymbol {V =} [/ latex] [латекс] \ boldsymbol {\ frac {Q} {C_S}} [/ latex] [латекс] \ boldsymbol {= V_1 + V_2 + V_3}. [/ Латекс ]

Вводя выражения для [latex] \ boldsymbol {V_1} [/ latex], [latex] \ boldsymbol {V_2} [/ latex] и [latex] \ boldsymbol {V_3} [/ latex], получаем

[латекс] \ boldsymbol {\ frac {Q} {C_S} = \ frac {Q} {C_1} + \ frac {Q} {C_2} + \ frac {Q} {C_3}}.[/ латекс]

Отменяя [латекс] \ boldsymbol {Q} [/ latex] s, мы получаем уравнение для полной емкости в серии [латекс] \ boldsymbol {C_S} [/ latex] равным

[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {C_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {C_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {C_3}} [/ latex] [latex] \ boldsymbol {+ \ cdots}, [/ latex]

, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно. Выражение этой формы всегда приводит к общей емкости [латекс] \ boldsymbol {C_S} [/ latex], которая меньше любой из отдельных емкостей [латекс] \ boldsymbol {C_1} [/ latex], [латекс] \ boldsymbol {C_2} [/ latex],…, как показано в следующем примере.

Общая емкость в серии,

C _с

Общая емкость в серии: [латекс] \ boldsymbol {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} + \ cdots } [/ latex]

Пример 1: Что такое последовательная емкость?

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 [латекс] \ mu \ textbf {F} [/ latex].

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.

Решение

Ввод заданных емкостей в выражение для [latex] \ boldsymbol {\ frac {1} {C_S}} [/ latex] дает [latex] \ boldsymbol {\ frac {1} {C_S} = \ frac {1} { C_1} + \ frac {1} {C_2} + \ frac {1} {C_3}} [/ латекс].

[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.000 \; \ mu \ textbf {F}}} [/ latex] [latex] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {5.000 \; \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {8.000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol { =} [/ latex] [латекс] \ boldsymbol {\ frac {1.325} {\ mu \ textbf {F}}} [/ latex]

Инвертирование для поиска [latex] \ boldsymbol {C_S} [/ latex] дает [latex] \ boldsymbol {C_S = \ frac {\ mu \ textbf {F}} {1.325} = 0.755 \; \ mu \ textbf {F} }[/латекс].

Обсуждение

Общая последовательная емкость [латекс] \ boldsymbol {C_s} [/ latex] меньше наименьшей индивидуальной емкости, как было обещано.При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,

[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {40} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {8} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {5} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {53} {40 \; \ mu \ textbf {F}}}, [/ латекс]

, так что

[латекс] \ boldsymbol {C_S =} [/ latex] [латекс] \ boldsymbol {\ frac {40 \; \ mu \ textbf {F}} {53}} [/ latex] [латекс] \ boldsymbol {= 0 .755 \; \ mu \ textbf {F}}. [/ latex]

На рис. 2 (а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс] \ boldsymbol {\ textbf {C} _ {\ textbf {p}}} [/ latex], сначала отметим, что напряжение на каждом конденсаторе составляет [латекс] \ boldsymbol {V} [ / latex], то же самое, что и у источника, так как они подключаются к нему напрямую через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общий заряд [латекс] \ boldsymbol {Q} [/ latex] равен сумме индивидуальных сборов:

[латекс] \ boldsymbol {Q = Q_1 + Q_2 + Q_3}. [/ Latex]

Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение [латекс] \ boldsymbol {Q = CV} [/ latex], мы видим, что общий заряд составляет [латекс] \ boldsymbol {Q = C _ {\ textbf {p}} V} [/ latex], и индивидуальные расходы: [латекс] \ boldsymbol {Q_1 = C_1 V} [/ latex] , [латекс] \ boldsymbol {Q_2 = C_2 V} [/ latex] , и [латекс] \ boldsymbol {Q_3 = C_3 V} [/ латекс]. Ввод их в предыдущее уравнение дает

[латекс] \ boldsymbol {C _ {\ textbf {p}} V = C_1 V + C_2 V + C_3 V}. [/ Latex]

Исключая [латекс] \ boldsymbol {V} [/ latex] из уравнения, мы получаем уравнение для полной емкости в параллельном [латексе] \ boldsymbol {C _ {\ textbf {p}}} [/ latex]:

[латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 \ cdots} [/ latex].

Общая параллельная емкость — это просто сумма отдельных емкостей. (И снова «… » указывает на то, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в приведенном выше примере были подключены параллельно, их емкость была бы

.

[латекс] \ boldsymbol {C _ {\ textbf {p}} = 1.000 \; \ mu \ textbf {F} + 5.000 \; \ mu \ textbf {F} + 8.000 \; \ mu \ textbf {F} = 14.000 \; \ mu \ textbf {F}}. [/ latex]

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на Рисунке 2 (b).

Общая емкость параллельно,

C _p [латекс] \ boldsymbol {C _ {\ textbf {p}}} [/ latex]

Общая емкость параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 + \ cdots} [/ latex]

Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.

Рисунок 3. (a) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ идут последовательно; их эквивалентная емкость C _S меньше, чем у любого из них. (c) Обратите внимание, что C _S находится параллельно с C ₃ .Таким образом, общая емкость равна сумме C _S и C ₃ .

Смесь последовательной и параллельной емкости

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ([латекс] \ boldsymbol {C_1 = 1.000 \; \ mu \ textbf {F}} [/ latex ], [латекс] \ boldsymbol {C_2 = 5.000 \; \ mu \ textbf {F}} [/ latex] и [латекс] \ boldsymbol {C_3 = 8.000 \; \ mu \ textbf {F}} [/ latex]) и округлите ответ до трех десятичных знаков.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы [латекс] \ boldsymbol {C_1} [/ latex] и [латекс] \ boldsymbol {C_2} [/ latex] включены последовательно. Их комбинация, обозначенная на рисунке [латекс] \ boldsymbol {C_S} [/ latex], параллельна [латексу] \ boldsymbol {C_3} [/ latex].

Решение

Поскольку [латекс] \ boldsymbol {C_1} [/ latex] и [latex] \ boldsymbol {C_2} [/ latex] соединены последовательно, их общая емкость определяется выражением [латекс] \ boldsymbol {\ frac {1} {C_S } = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3}} [/ latex].Ввод их значений в уравнение дает

[латекс] \ boldsymbol {\ frac {1} {C_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {C_2}} [/ латекс ] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {1.000 \; \ mu \ textbf {F}}} [/ латекс] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {5.000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ гидроразрыв {1.200} {\ mu \ textbf {F}}}. [/ latex]

Инвертирование дает

[латекс] \ boldsymbol {C _ {\ textbf {S}} = 0.833 \; \ mu \ textbf {F}}. [/ Latex]

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет

[латекс] \ begin {array} {r @ {{} = {}} l} \ boldsymbol {C _ {\ textbf {tot}}} & \ boldsymbol {C_S + C_S} \\ [1em] & \ boldsymbol { 0.833 \; \ mu \ textbf {F} + 8.000 \; \ mu \ textbf {F}} \\ [1em] & \ boldsymbol {8.833 \; \ mu \ textbf {F}}. \ end {array} [/ latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к большим комбинациям конденсаторов.

• Общая емкость последовательно [латекс] \ boldsymbol {\ frac {1} {C _ {\ textbf {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1 } {C_3} + \ cdots} [/ латекс]
• Общая емкость параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 + \ cdots} [/ latex]
• Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.

Концептуальные вопросы

1: Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.

Задачи и упражнения

1: Найдите общую емкость комбинации конденсаторов на рисунке 4.

Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.

2: Предположим, вам нужна конденсаторная батарея с общей емкостью 0,750 Ф и у вас есть множество конденсаторов 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?

3: Какую общую емкость можно получить, подключив символ [латекс] \ bold {5.00 \; \ mu \ textbf {F}} [/ latex] и конденсатор [latex] \ boldsymbol {8.00 \; \ mu \ textbf {F}} [/ latex] вместе?

4: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.

Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.

5: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.

Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.

6: Необоснованные результаты

(a) Конденсатор [латекс] \ boldsymbol {8.00 \; \ mu \ textbf {F}} [/ latex] подключен параллельно другому конденсатору, что дает общую емкость [латекс] \ boldsymbol {5.00 \; \ mu \ textbf {F}} [/ латекс]. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Решения

Задачи и упражнения

1: [латекс] \ boldsymbol {0.293 \; \ mu \ textbf {F}} [/ латекс]

3: [латекс] \ boldsymbol {3.08 \; \ mu \ textbf {F}} [/ latex] в последовательной комбинации, [латекс] \ boldsymbol {13.0 \; \ mu \ textbf {F}} [/ латекс ] в параллельной комбинации

4: [латекс] \ boldsymbol {2.79 \; \ mu \ textbf {F}} [/ латекс]

6: (a) [латекс] \ boldsymbol {-3.00 \; \ mu \ textbf {F}} [/ latex]

(b) У вас не может быть отрицательного значения емкости.

(c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным.Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.

Емкостное реактивное сопротивление

— Как найти последовательные и параллельные конденсаторы

Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.

Шаг 1: Найдите общую емкость цепи

Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц.Каково полное емкостное реактивное сопротивление (X _C ) при последовательном или параллельном подключении?

1А. Для конденсаторов серии

Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.

Конденсаторы серии

Пример:

1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033

0,083 + 0,050 + 0,033 = 0,166

1 / 0,163 = 6,02 мкФ

Примечание: математические расчеты упрощены для целей иллюстрации. Для более точных чисел воспользуйтесь калькулятором.

1Б. Для параллельных конденсаторов

При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов.Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.

Параллельные конденсаторы Пример:

12 + 20 + 30 = 62 мкФ

---

Шаг 2: Определите емкостное сопротивление

Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, и поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X _C ) который измеряется в Ом.

Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока протекает. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.

X _C — емкостное реактивное сопротивление в омах, f — частота в герцах и C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!

1 мкФ = 0,000001 F

Серия 60 Гц Пример:

6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом

Параллельный 60 Гц Пример:

62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом

Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :

Серия 400 Гц Пример:

2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом

Параллельный 400 Гц Пример:

2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом

---

Полезные ссылки

.